ESTUDIO DE LA RELACIÓN ENTRE LA “PREDISPOSICIÓN DESFAVORABLE HACIA LA MATEMÁTICA” Y LA “AUTOCONFIANZA MATEMÁTICA” EN ESTUDIANTES DE SECUNDARIA EN UN COLEGIO DE LA PROVINCIA DE CARTAGO, COSTA RICA.

Study of the relationship between “unfavorable predisposition towards mathematics” and “mathematical self-confidence” in secondary school students in a school in the province of Cartago.

Revista Trama

Volumen 10, número 2

Julio - Diciembre 2021

Páginas 124-152

ISSN: 1659-343X

https://revistas.tec.ac.cr/trama

María Laura Solano García1 / Karla Garro Camacho 2 / Luis Gerardo Meza Cascante 3

Fecha de recepción: 2 de setiembre, 2021

Fecha de aprobación: 22 de abril, 2022

Solano, M., Garro, K. y Meza, L. (2021). Estudio de la relación entre la "predisposición desfavorable hacia el aprendizaje de la matemática" y la "autoconfianza matemática" en estudiantes de secundaria en un colegio de la provincia de Cartago, Costa Rica. Trama, Revista de ciencias sociales y humanidades, Volumen 10, (2), Julio-Diciembre, págs. 124-152.

DOI: https://doi.org/10.18845/tramarcsh.v10i2.6306

Se presentan los resultados de un estudio en estudiantes de educación secundaria en un colegio de la provincia de Cartago, Costa Rica, cuyo nombre se reserva por acuerdo de confidencialidad, realizado en el primer semestre del año 2020 con una muestra de 341 estudiantes de una población de 371 estudiantes.

El objetivo de la investigación fue estudiar la relación entre las variables “predisposición desfavorable hacia la matemática” y “autoconfianza matemática”, analizando la existencia de diferencias según el sexo y el nivel educativo. Se utilizaron la “Escala de Predisposición hacia las Matemáticas (EPMAT)” de Cerda, Ortega, Casas, Del Rey y Pérez (2016) y la “Escala de Autoconfianza Matemática” de Fennema-Sherman (1976).

Los resultados indican que aproximadamente el 88,9% de los estudiantes muestran un nivel de “predisposición desfavorable hacia la matemática” alto y que aproximadamente un 87,1% manifiestan un nivel de “autoconfianza matemática” bajo. Se encontró que las mujeres presentan valores, en promedio, más bajos de “predisposición desfavorable hacia la matemática” y más altos de “autoconfianza matemática”.

No se encontraron diferencias en el estudiantado por nivel educativo en ninguna de las dos variables. Finalmente, la investigación determinó la existencia de una relación inversa, fuerte y significativa entre las variables.

Palabras clave: matemática, predisposición desfavorable hacia la matemática, autoconfianza matemática, factores afectivos, enseñanza.

The results of a study on secondary education students in a school in the province of Cartago, Costa Rica, whose name is reserved by confidentiality agreement, carried out in the first semester of 2020 with a sample of 341 students from a population of 371 students are presented.

8.9% of the students show a high level of “unfavorable predisposition towards mathematics” The objective of the research was to study the relationship between the variables “unfavorable predisposition towards mathematics” and “mathematical self-confidence”, analyzing the existence of differences according to sex and educational level. The “Predisposition towards Mathematics Scale (EPMAT)” by Cerda, Ortega, Casas, Del Rey, and Pérez (2016) and the “Mathematical Self-Confidence Scale” by Fennema-Sherman (1976) were used.

The results indicate that approximately 8 and that approximately 87.1% show a low level of “mathematical self-confidence”. It was found that women have lower values, on average of “unfavorable predisposition towards mathematics” and higher values of mathematical self-confidence.

No differences were found in the student body by educational level in any of the two variables. Finally, the research determined the existence of an inverse, strong and significant relationship between the variables.

Key words: mathematics, unfavorable predisposition towards mathematics, mathematical self-confidence, affective factors, teaching.

Las personas investigadoras han tomado conciencia paulatinamente de la influencia de los factores afectivos en el aprendizaje de la matemática y, por este motivo, en los últimos años se ha incrementado el número de trabajos que profundizan en esa temática (Gómez-Chacón, 2010).

Gil, Blanco y Guerrero (2005) afirman que es de gran importancia el estudio de los factores afectivos para conocer su influencia, con la intención de promover actitudes y creencias positivas en el alumnado que redunden en la mejora del rendimiento y las expectativas de logro hacia esta materia.

La “predisposición desfavorable hacia la matemática” y la “autoconfianza matemática” juegan un papel fundamental en el proceso de enseñanza aprendizaje de la matemática, es por esa razón que han aumentado la cantidad de investigaciones relacionadas con estos aspectos.

De acuerdo con Cerda, Pérez, Aguilar y Aragón (2018), se entiende por “predisposición desfavorable hacia la matemática” la percepción desfavorable hacia el enfrentamiento o abordaje de tareas en el ámbito matemático. Se expresa como disgusto, desagrado, falta de perseverancia o desinterés hacia las tareas matemáticas.

Zabalza (1994), citado por Muñoz y Mato (2006), plantea que nadie nace con predisposición positiva o negativa hacia algo, señalando que la forma en que se adquieren las actitudes es variada, proviniendo de experiencias positivas o negativas con el objeto de la actitud.

Una predisposición desfavorable hacia la matemática influye negativamente en el rendimiento escolar, del mismo modo que un estudiante con alta motivación tiende a involucrarse más en las tareas desplegando un mayor esfuerzo, lo que se asocia a un mejor rendimiento, pero a la vez se relaciona en forma negativa con el estado de ansiedad, especialmente en los estudiantes varones (Marchand y Skinner, 2007; Skaalvik y Skaalvik, 2005; Yaratan y Kasapoğlu, 2012).

La “autoconfianza matemática” se refiere, según Fennema y Sherman (1976), citadas por Pérez-Tyteca et al. (2013), a la confianza que el sujeto tiene en su propia habilidad para aprender y desempeñar satisfactoriamente una tarea matemática, y aseguran que está ligado al grado en que el alumno está dispuesto a esforzarse para realizar el trabajo que se le asigna.

Pérez-Tyteca (2012) considera la “autoconfianza matemática” como una creencia sobre la propia competencia matemática que consiste en la confianza que un sujeto tiene en sus propias habilidades para enfrentarse a tareas relacionadas con la matemática.

Varias investigaciones han encontrado diferencias en cuanto a la autoconfianza matemática, según el sexo, con mejores resultados para los hombres (Gil et al., 2006a, 2006b). González-Pienda et al. (2006), citado por Gamboa (2012), en un estudio con estudiantes brasileños, tanto de primaria como de secundaria, encontraron que las mujeres manifestaron una mayor desconfianza en sus logros en el área de la matemática (p.70).

Sherman (1983), Reyes (1984) y McLeod (1992), citados por Pérez-Tyteca (2012), también concluyen que las investigaciones realizadas sugieren que existen diferencias por sexo en el nivel de “autoconfianza matemática”, aun cuando las mujeres no tienen razones para ser menos autoconfiadas, ya que su desempeño no es peor que el de los hombres.

En el caso costarricense, investigaciones desarrolladas por Arrieta (2016), Calderón y Guillén (2016), Ramos (2015) y Agüero, Calderón, Meza y Suárez (2016) evidenciaron la existencia de diferencias en el nivel de “autoconfianza matemática” según el sexo, concluyendo que las mujeres manifiestan niveles menores de “autoconfianza matemática” que los hombres. Brown y Josephs (2001) señalan que las diferencias entre los hombres y las mujeres en su nivel de “autoconfianza matemática”, se debe, posiblemente, a los estereotipos sociales y a otros factores que inhiben a las mujeres a tomar tantos cursos de matemáticas como los hombres.

Pérez-Tyteca (2012) expone que en distintas investigaciones se ha hallado una correlación positiva entre la “autoconfianza matemática” y el rendimiento académico, esto es, cuanta más confianza posee un sujeto en sus propias habilidades matemáticas mejor es su rendimiento y viceversa, resultados que coincide con los de Arrieta (2016). No obstante, Pérez-Tyteca (2012) advierte que considera difícil establecer una relación causal entre esas variables.

La matemática es una asignatura hacia la que muchos estudiantes muestran una predisposición de carácter negativo, e incluso rechazo, por diversos motivos, como pueden ser el método utilizado, las expectativas y estilo del profesor y la influencia de los estereotipos basados en factores sociales y culturales (Guven y Cabakcor, 2013; Moenikia y Zahed-Babelan, 2010; Yaratan y Kasapoğlu, 2012).

Dicha predisposición ha resultado importante a la hora de explicar la variabilidad de los rendimientos académicos generales, y en matemáticas, de los estudiantes en modelos complejos de interacción con otras variables, como la inteligencia lógica, los esquemas de razonamiento formal, como también con el nivel de competencias matemáticas tempranas y factores de convivencia escolar (Cerda, Romera, Casas, Pérez y Ortega-Ruiz, 2017).

Al mismo tiempo, algunas investigaciones señalan que una disposición desfavorable hacia la matemática influye negativamente en el rendimiento escolar y una disposición positiva favorece el rendimiento en esta asignatura (Cerda et al., 2016).

Esta predisposición puede tener su génesis en distintos factores que el estudiante acumula a lo largo de su paso por la escuela al aprender matemática, lo que incide de forma relevante en la formación de sus creencias y emociones acerca de ella (Gómez-Chacón, 2007; Hidalgo, Maroto y Palacios, 2004).

Lo que se piensa sobre la naturaleza de la matemática, la manera de usarla, cómo y para qué se aprende y cuán útil es para la sociedad, no sólo da cuenta de componentes de tipo intelectual o cognitivo, sino que está ligado a una serie de elementos del dominio afectivo, como sentimientos o emociones, que movilizan o inciden en aspectos volitivos emocionales de los estudiantes hacia esta asignatura (Hailikari, Nevgi y Komulainen, 2008).

Con estos elementos como sustento, la investigación se centró en estudiar la existencia de una relación entre el nivel de “predisposición desfavorable hacia la matemática” y el de “autoconfianza matemática”, en estudiantes de secundaria de un colegio de la provincia de Cartago, Costa Rica, indagando sobre la existencia de diferencias en el nivel de esas variables por sexo o nivel educativo.

La investigación, cuyos resultados se reportan en este artículo, constituye un elemento más de un conjunto de estudios desarrollados en el Instituto Tecnológico de Costa Rica en el llamado “dominio afectivo” en el campo de la educación matemática, que aporta de manera pionera resultados sobre la relación entre las variables “predisposición desfavorable hacia la matemática” y el de “autoconfianza matemática” en estudiantes de la educación secundaria costarricense.

La investigación es de carácter cuantitativo, clasificable como descriptiva y correlacional, con una muestra de 341 estudiantes de un total de 371 estudiantes matriculados en el primer semestre del 2020 en el centro educativo. La muestra se integró con el total de estudiantes que respondieron la encuesta el día de su aplicación, a partir de la pretensión de hacer una aplicación al total de estudiantes.

La distribución de la muestra por sexo y nivel educativo se presenta en las Tablas 1 y 2.

Tabla 1. Distribución de los estudiantes de la muestra por sexo

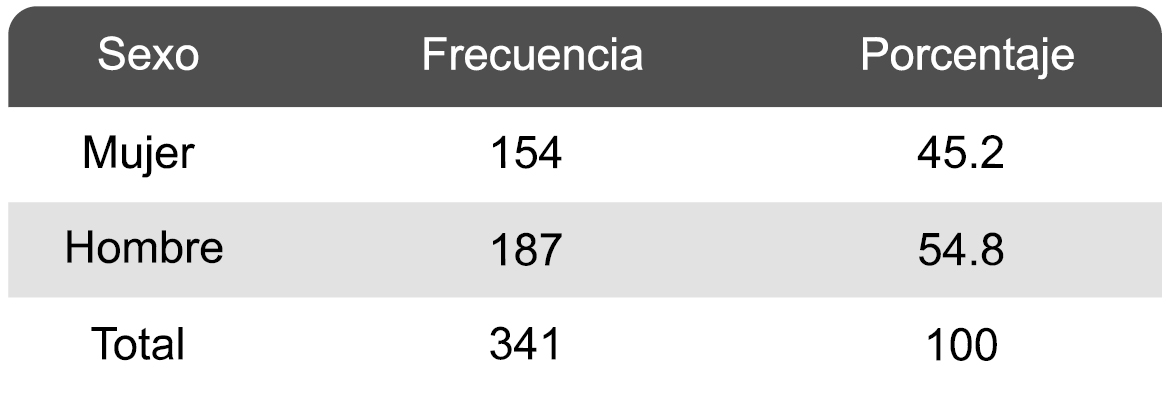
Fuente: Elaboración propia.

Tabla 2. Distribución de los estudiantes de la muestra por niveles

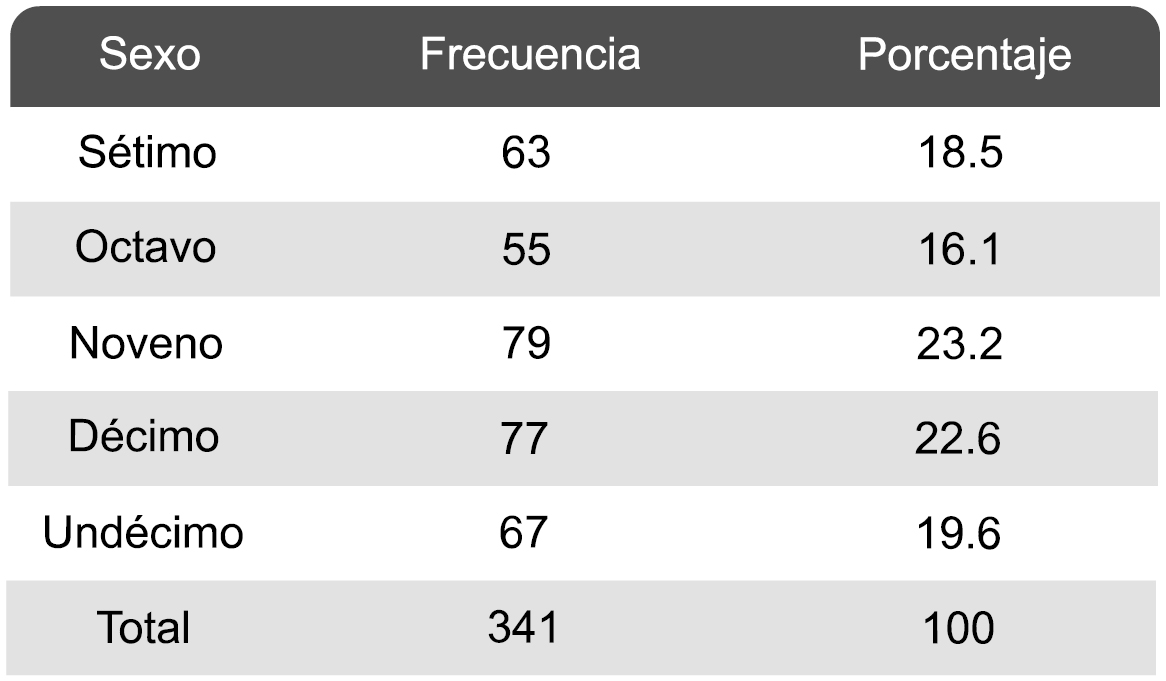
Fuente: Elaboración propia.

Las variables consideradas en la investigación son: sexo, predisposición desfavorable hacia la matemática, autoconfianza matemática y nivel educativo. La Tabla 3 presenta la definición conceptual y operativa de estas variables.

Tabla 3. Definición conceptual y operativa de las variables.

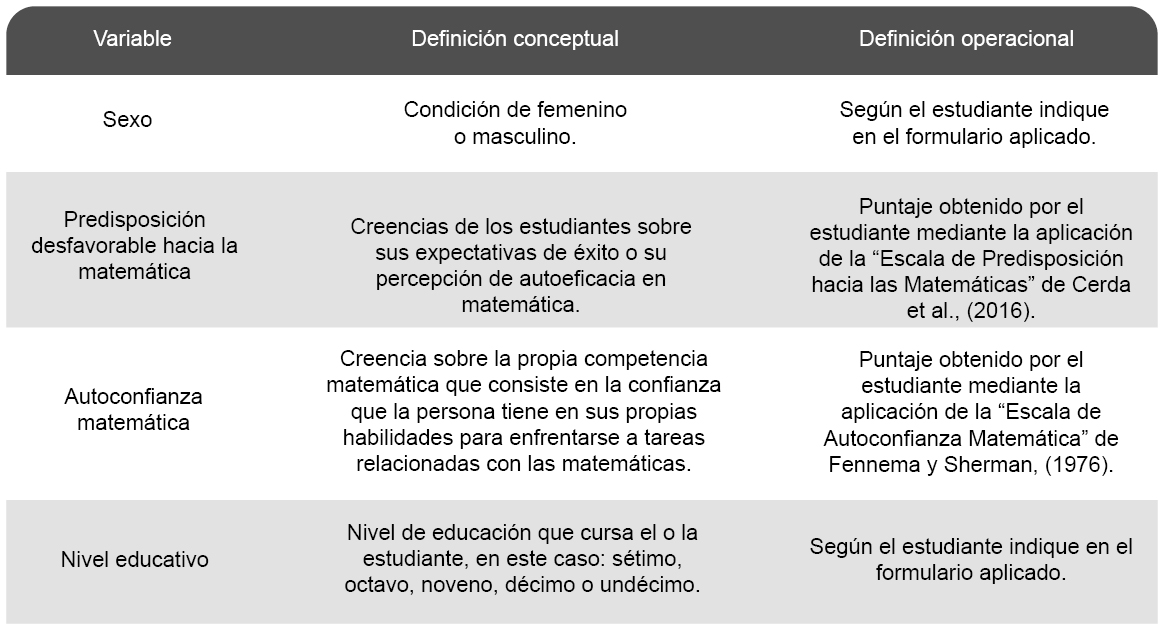
Fuente: Elaboración propia.

Como instrumentos de medición se utilizaron la “Escala de Predisposición hacia las Matemáticas (EPMAT)”, creada y validada por Cerda et al. (2016) y la “Escala de Autoconfianza Matemática” creada por Fennema y Sherman (1976).

Ambas escalas consisten en cuestionarios tipo Likert, de seis ítems y doce ítems, respectivamente; con cinco posibilidades de respuesta desde “Totalmente de acuerdo” a “Totalmente en desacuerdo”, con la opción central de “Indeciso”.

Como parte del estudio de la validez se calcularon los índices de discriminación de los ítems, y se obtuvo valores superiores a 0.5 en todos los casos, lo que indica que discriminan muy bien (Lozano y De la Fuente-Solana, 2013).

Además, se estudió el supuesto de unidimensionalidad de cada escala utilizando el análisis factorial, por ser la técnica más utilizada para estos propósitos (Jiménez y Montero, 2013, p. 6), con el cálculo previo del índice de Kaiser-Meyer-Olkin (KMO). Los valores de KMO de 0,855 para “predisposición desfavorable hacia la matemática”, y de 0.942 para “autoconfianza matemática”, permiten considerar como buena y excelente la adecuación muestral, respectivamente, según la clasificación de Kaiser (1974), citado por Frías-Navarro y Pascual (2012). Además, el índice de Bartlett de valor 0 para ambas escalas, indica que es aceptable el uso del análisis factorial a los datos recabados.

El análisis factorial produjo un primer factor que explica al menos el 66,392% de la varianza para la “predisposición desfavorable hacia la matemática” y un 57,742% de la varianza para la “autoconfianza matemática”, lo que evidencia la unidimensionalidad de cada escala, de acuerdo con el criterio de Carmines y Zeller (1979, citado en Burga (2006).

La confiabilidad de cada instrumento (la fiabilidad de la escala) fue estudiada mediante la técnica “Alfa de Cronbach”, utilizando como referencia el criterio de Cea (1999), que establece que un valor igual o superior a 0.8 indica una confiabilidad apropiada. Para la primera escala se obtuvo un valor de 0.867 y para la segunda escala un valor de 0.931, ambas mostrando una adecuada discriminación.

La investigación sometió a prueba las siguientes cinco hipótesis:

•No existen diferencias en el nivel de “predisposición desfavorable hacia la matemática”, según el sexo.

•No existen diferencias en el nivel de “autoconfianza matemática”, según el sexo.

•No existen diferencias en el nivel de “predisposición desfavorable hacia la matemática”, según el nivel educativo.

•No existen diferencias en el nivel de “autoconfianza matemática”, según el nivel educativo.

•No existe relación entre el nivel de “predisposición desfavorable hacia la matemática” y el nivel de “autoconfianza matemática”.

Para la prueba de las hipótesis se utilizaron métodos paramétricos (T-Student o ANOVA, según correspondiera) cuando se pudo asumir la normalidad de los datos o métodos no paramétricos en caso contrario (U de Mann-Whitney y Kruskal-Wallis complementada con la prueba “a posteriori” de Dunn). Cuando se detectaron diferencias entre las medias de alguna de las dos variables en alguna de las categorías en contraste se calcularon los tamaños del efecto, mediante el cálculo del coeficiente d de Cohen, cuya interpretación se realizó siguiendo las recomendaciones de Cohen: cerca de 0.2 es una diferencia pequeña, cerca de 0.5 es moderada y superior a 0.8 es grande. (Morales-Vallejo, 2012)

Finalmente, para estudiar la existencia de correlación entre las variables “predisposición desfavorable hacia la matemática” y “autoconfianza matemática” se aplicó el coeficiente de correlación de Pearson, previa prueba de hipótesis de que este coeficiente no era nulo.

Clasificación del nivel de “predisposición desfavorable hacia la matemática” y del nivel de “autoconfianza matemática”

El valor medio de la escala de la “predisposición desfavorable hacia la matemática” corresponde a 18. La media de esta variable para la muestra (M = 20.76, SD = 3.98) resultó significativamente mayor que el valor promedio de la escala (t (340) = 26.68, p < 0.05), lo que interpretado de manera global indica que el estudiantado presenta un nivel de “predisposición desfavorable hacia la matemática” superior al valor promedio; esto es, presentan niveles altos en esta variable.

Por su parte, el valor medio de la escala de la “autoconfianza matemática” corresponde a 36. El valor medio de esta variable para la muestra (M = 22.71, SD = 8.77) resultó significativamente menor que el valor promedio de la escala (t (340) = -21.66, p < 0.05), lo que interpretado de manera global indica que el estudiantado presenta un nivel de “autoconfianza matemática” inferior al valor promedio; esto es, presentan niveles bajos en esta otra variable.

Se clasifican los niveles de “autoconfianza matemática” y de “predisposición desfavorable hacia la matemática” en dos categorías: baja o alta, según el puntaje sea menor o mayor, respectivamente, al valor medio de la escala correspondiente, con los resultados que se presentan en la Tabla 4.

Tabla 4. Clasificación del nivel de “autoconfianza matemática” y de “predisposición desfavorable hacia la matemática”

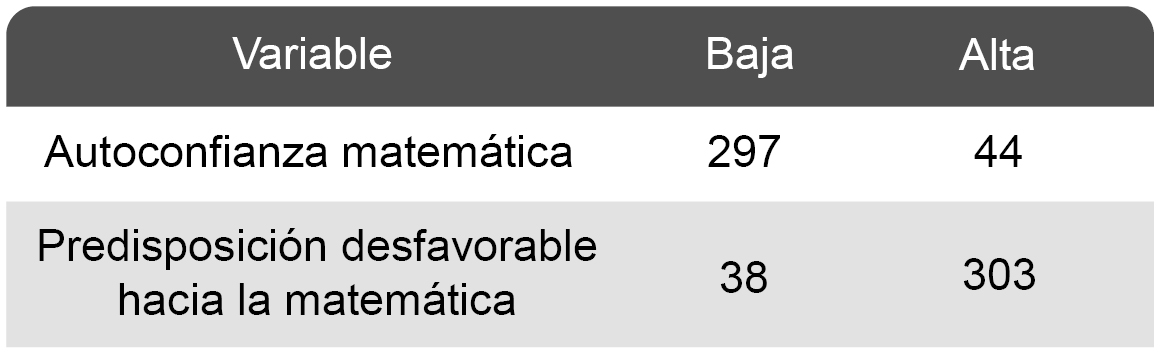
Fuente: Elaboración propia.

Contraste de hipótesis

A continuación, se presentan los resultados del análisis de las hipótesis planteadas en el estudio.

Contraste de la hipótesis No.1

La normalidad de la distribución de los datos, para el estudio de la hipótesis 1, se asume con base en el teorema del límite central debido a que cada categoría involucrada en el contraste contiene más de 100 datos. (Aguayo, 2004)

Para analizar la igualdad de varianzas se aplicó la prueba de Levene y la prueba T-Student para la igualdad de medias con los resultados de la Tabla 5 y Tabla 6, respectivamente.

Tabla 5. Resultados de la prueba Levene para la variable “predisposición desfavorable hacia la matemática”

Fuente: Elaboración propia.

Dado que el valor de la significancia es 0.073, que es mayor que 0.05, se considera que las varianzas son homogéneas.

Tabla 6. Resultados de la prueba T-Student para la variable “predisposición desfavorable hacia la matemática”

Fuente: Elaboración propia.

Dado que p < 0.05 se rechaza la hipótesis nula y se tiene evidencia estadística de la diferencia significativa entre hombres y mujeres, para la variable “predisposición desfavorable hacia la matemática”, con valor promedio menor para las mujeres.

Se procede a calcular el “tamaño del efecto”, para obtener el valor d= 0.2527, que se interpreta como bajo, de acuerdo con la clasificación dada por Cohen (Morales-Vallejo, 2012): en torno a 0.20 diferencia pequeña, en torno a 0.50 diferencia moderada y 0.80 o más diferencia grande.

Contraste de la hipótesis No.2

La normalidad de la distribución de los datos se asume también en este caso con base en el teorema del límite central, debido a que cada categoría involucrada en el contraste contiene más de 100 datos. (Aguayo, 2004)

Los resultados de la prueba de Levene, aplicada para estudiar la igualdad de varianzas y la prueba T-Student para estudiar la igualdad de medias para la variable “autoconfianza matemática”, se muestran en la Tabla 7 y Tabla 8, respectivamente.

Tabla 7. Resultados de la prueba Levene para la variable autoconfianza

Fuente: Elaboración propia.

De acuerdo con los resultados de la Tabla 13, no se puede asumir homogeneidad en las varianzas, ya que el valor de la significancia es cero (p <0.05).

Tabla 8. Resultados de la prueba T-Student para la variable “autoconfianza matemática”

Fuente: Elaboración propia.

Al observar el valor de la significancia tenemos que el valor corresponde a 0, el cual es menor que 0.05 (p<0.05), por lo que se procede a rechazar la hipótesis nula y aceptar la hipótesis alternativa, lo que significa que existen diferencias entre mujeres y hombres en la variable “autoconfianza matemática”, con valores en promedio mayores para las mujeres.

Se calcula el “tamaño del efecto”, para obtener el valor d= 0.4541, que se interpreta como moderado, de acuerdo con la clasificación dada por Cohen (Morales-Vallejo, 2012).

Contraste de la hipótesis No.3

Para esta hipótesis se aplica la prueba no paramétrica de Kruskal-Wallis, porque las distribuciones de las muestras en contraste no muestran normalidad. Los resultados de esta prueba para la variable “predisposición desfavorable hacia la matemática” se presentan en la Tabla 9.

Tabla 9. Prueba de Kruskal-Wallis para la variable “predisposición desfavorable hacia la matemática”

Fuente: Elaboración propia.

Se observa que el valor de significancia es de 0.529, el cual es mayor al 5% (p>0.05), por lo que se acepta la hipótesis nula. Es decir, no se encuentran diferencias en cuanto a la “predisposición desfavorable hacia la matemática” por nivel educativo.

Contraste de la hipótesis No.4

Al considerar de nuevo que el nivel educativo tiene cinco categorías, y que no se puede asumir el supuesto de normalidad, se procede de igual manera a aplicar la prueba no paramétrica Kruskal-Wallis, con los resultados de la Tabla 10.

Tabla 10. Prueba de Kruskal-Wallis para la variable “autoconfianza matemática”

Fuente: Elaboración propia.

Se acepta la hipótesis nula ya que p>0.05. Por tanto, se concluye que no existen diferencias en el nivel de “autoconfianza matemática”, según el nivel educativo.

Contraste de la hipótesis No.5

Para estudiar esta hipótesis se analizan los valores de las correlaciones de la Tabla 11, en la que se señala con dos asteriscos que son significativas (es decir, que se rechaza la hipótesis nula de que los coeficientes de correlación sean nulos).

Tabla 11. Correlaciones entre las variables

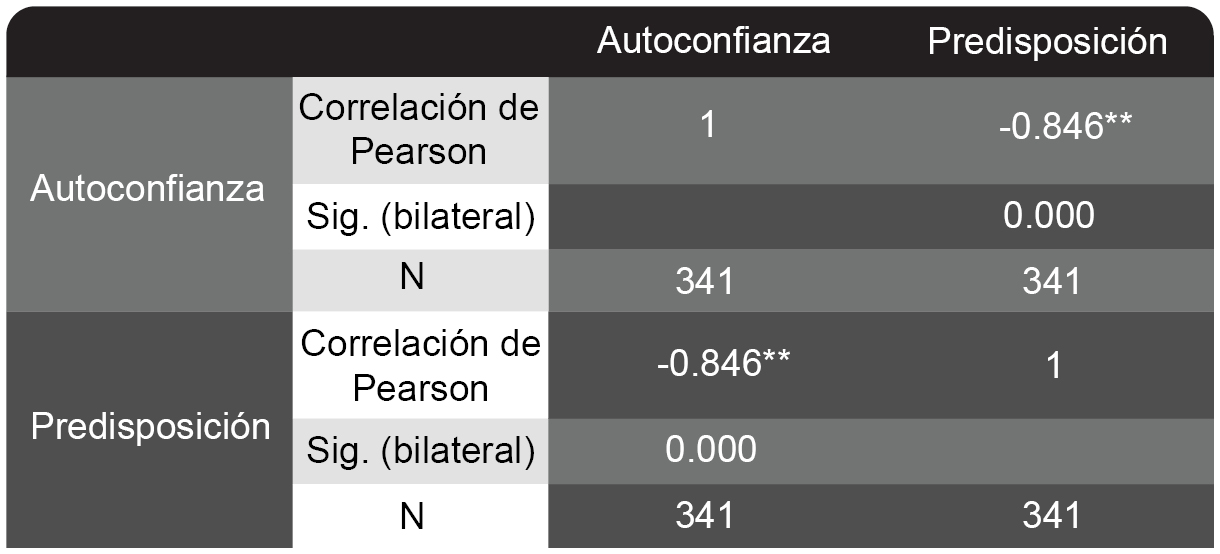
**. La correlación es significativa al nivel 0,01 (bilateral).

Fuente: Elaboración propia.

De la Tabla 18 se desprende que existe correlación significativa entre las variables, dado que presenta un nivel de 0.01, razón por lo que corresponde rechazar la hipótesis nula, y aceptar la hipótesis alternativa.

El signo negativo del coeficiente de correlación de Pearson indica que se da una relación inversa entre las variables estudiadas. Además, según Aguayo (2004), al calcular el valor absoluto del coeficiente de Pearson, (en este caso |-0.846|=0.846), al ser mayor a 0.70, se considera que la asociación entre ambas variables es fuerte.

La investigación se enfocó en estudiar las variables “predisposición desfavorable hacia la matemática” y “autoconfianza matemática” en la población estudiantil de secundaria de un colegio en la provincia de Cartago, indagando sobre la existencia de diferencias por sexo o nivel educativo, y sobre la relación entre estas dos variables, a partir de la convicción de la importancia del “dominio afectivo” en el proceso de aprendizaje de la matemática.

La mayoría del estudiantado, un 88.9%, mostró un nivel de “predisposición desfavorable hacia la matemática” alto, lo que se comprueba con el hecho de que el valor medio de esta variable en la muestra es significativamente superior al valor medio de la escala. Este es un hallazgo que sugiere la necesidad de que se desarrolle un proyecto de intervención educativa enfocado en mejorar la predisposición hacia la matemática con la intencionalidad de mejorar, a su vez, el rendimiento académico en la disciplina (Marchand y Skinner, 2007; Skaalvik y Skaalvik, 2005; Yaratan y Kasapoğlu, 2012).

Por su parte, un 87.1% mostró niveles de “autoconfianza matemática” bajo, y, de manera concordante, el valor de la media en esta variable fue significativamente inferior al valor medio de la escala. Los resultados son concordantes con los hallazgos de Coto (2018), los cuales sustentan que aproximadamente el 75.9% del estudiantado presenta niveles entre bajo o medio, mas no coinciden con los reportados en Agüero et al. (2016) o en Meza et al. (2019), ya que en estos estudios, realizados en la educación media costarricense en colegios públicos diurnos, casi el 79% de estudiantes mostró niveles entre alto y moderado. Los resultados de la investigación también sugieren, en términos prácticos, la conveniencia de que en la institución se desarrollen acciones de intervención educativa enfocadas en mejorar el nivel de “autoconfianza matemática” con la esperanza de mejorar el rendimiento académico, aunque no se pueda asegurar causalidad entre estas dos variables (Pérez-Tyteca (2012).

Debe observarse, además, que tales esfuerzos institucionales por mejorar el nivel de estas dos variables del “dominio afectivo” en educación matemática, resulta totalmente concordante con las disposiciones de los programas de matemática vigentes en Costa Rica, aprobados por el Consejo Superior de Educación en el año 2012, que procuran la “potenciación de actitudes y creencias positivas en torno a las Matemáticas” (Ministerio de Educación Pública, 2012, p. 11), desarrollando la perseverancia, la confianza en la utilidad de la matemática y promoviendo la participación activa y colaborativa en el proceso de aprendizaje, así elevar el autoestima en relación con el dominio de la matemática y el respeto, aprecio y disfrute de esta materia.

Los resultados de la investigación permiten concluir, en relación con la “predisposición desfavorable hacia la matemática”, que las mujeres presentan valores en promedio más bajos que los hombres, es decir, se detectaron diferencias en esta variable con respecto al sexo, resultado coincidente con los hallazgos Del Río et al. (2016). A su vez, no se encontraron diferencias en esta variable entre los estudiantes por nivel educativo.

Por otro lado, en relación con la “autoconfianza matemática”, la investigación concluye que las mujeres muestran valores en promedio más altos que los hombres, aspecto que permite concluir que existen diferencias en el nivel de “autoconfianza matemática” según el sexo, resultado que coincide con los obtenidos en el ámbito internacional por Brown y Josephs (2001), Sherman (1983), Reyes (1984) y McLeod (1992), citados por Pérez-Tyteca (2012).

Es relevante destacar que este hallazgo no es concordante con los resultados de otras investigaciones realizadas en el ámbito costarricense, en las que las diferencias en la variable “autoconfianza matemática” según el sexo señalan niveles, en promedio, más altos para los varones (Ramos, 2015, Meza et al., 2016 y Calderón y Guillén, 2016, en educación secundaria oficial diurna, Arrieta, 2016, Sánchez y Jiménez, 2016, Morales y Arce, 2017, Vega, 2017 y Báez, 2019, en educación universitaria), más sí lo es con los de Wynta y López (2017) en educación superior.

Por otro lado, no se encontraron diferencias en esta variable según el nivel educativo, lo que contrasta con los hallazgos de otras investigaciones realizadas en el ámbito costarricense, como las de Ramos (2015), Meza et al. (2016) y Calderón y Guillén (2016), en educación secundaria oficial diurna o Arrieta (2016), Sánchez y Jiménez (2016), Morales y Arce (2017), Vega (2017) y Báez (2019), en educación superior.

No obstante, aunque se detectaron diferencias en esas variables según el sexo, los tamaños del efecto resultaron pequeños o moderados, respectivamente, lo que se puede interpretar en términos prácticos como que no es necesario diferenciar las acciones que emprenda la institución para mejorar los niveles en estas dos variables según el sexo de las y los estudiantes, por lo que se puede considerar que las acciones de intervención educativa no tienen por qué ser diferentes para las mujeres y para los hombres.

Los resultados discordantes con los de otras investigaciones realizadas en el ámbito nacional, en las que las mujeres resultan con niveles menos favorables que los hombres, es un aporte más para sustentar que las diferencias observadas pueden tener su justificación en los estereotipos culturales acerca de la matemática y el sexo, particularmente en el papel que pueden desempeñar las mujeres en temáticas relacionadas con esta asignatura, y no en razones de capacidad intelectual de alguno de los dos sexos para hacer o aprender matemática.

Para finalizar, en cuanto a la relación entre ambos constructos (predisposición desfavorable hacia la matemática y autoconfianza matemática), se encuentra un índice de correlación negativo, fuerte y significativo, lo que permite inferir que los estudiantes que muestran bajos niveles de “predisposición desfavorable hacia la matemática” presentan, en términos generales, altos niveles de “autoconfianza matemática”.

Aunque la investigación no tiene capacidad explicativa, esto es, no se puede inferir una relación causal entre estas variables, los resultados permiten esperar que la mejoría de una de las variables pueda estar ligada a la mejoría en la otra. Por tanto, desde una perspectiva práctica, se puede recomendar que la acción institucional para mejorar el nivel en estas variables pueda enfocarse en una de ellas con la esperanza de que también pueda tener resultados positivos para la otra, eso sí, con la clara conciencia de que no necesariamente suceda de esa manera.

Se agradece al colegio participante, cuyo nombre se mantiene en secreto por el compromiso de confidencialidad adquirido y a las y los estudiantes que conformaron la muestra. También se agradece a los profesores Mag. Randall Blanco Benamburg, Lic. Paulo García Delgado, Dra. Zuleyka Suárez Valdés-Ayala y Dra. Evelyn Agüero Calvo, de la Escuela de Matemática del Tecnológico de Costa Rica, por sus aportaciones en la revisión de la tesis que originó la investigación como integrantes del tribunal evaluador.

Aguayo, M. (2004). Cómo realizar “paso a paso” un contraste de hipótesis con SPSS para Windows y alternativamente con EPIINFO y EPIDAT: (II) Asociación entre una variable cuantitativa y una categórica (comparación de medias entre dos o más grupos independientes). Recuperado de http://www.fabis.org/html/ archivos/docuweb/contraste_hipotesis_2r.pdf

Agüero, E., Calderón, M., Meza, G. & Suárez, Z (2016). Relación entre autoestima y autoconfianza matemática en estudiantes de educación media costarricense. Revista Comunicación. Año 37, volumen 25, número 2, julio – diciembre, 2016. Instituto Tecnológico de Costa Rica. ISSN: 0379-3974 / e-ISSN1659-3820. .

Arrieta, M. (2016). Relación entre el rendimiento académico y el nivel de “autoconfianza matemática” y de “ansiedad matemática” en estudiantes del curso MA1103 Matemática Básica para Administración del Instituto Tecnológico de Costa Rica (Tesis de licenciatura inédita). Instituto Tecnológico de Costa Rica, Cartago.

Báez, N. (2019). Estudio de la relación entre la “ansiedad matemática”, la “autoconfianza matemática” y la “actitud hacia utilidad de la matemática” en estudiantes de carreras administrativas en una universidad privada de Costa Rica. (Tesis inédita de licenciatura) Instituto Tecnológico de Costa Rica.

Brown, R. P. y Josephs, R. A. (2001). El peso de la prueba: Diferencias de género y relevancia de los estereotipos en el desempeño matemático. Nómadas, 14, 110-123. Recuperado de http://www.redalyc.org/pdf/1051/105115268010.pdf

Burga, A. (2006). La unidimensionalidad de un instrumento de medición: perspectiva factorial. Revista de Psicología de la PUCP, XXIV (1), 53-80.

Calderón, P. y Guillén, C. (2016). Estudio sobre “autoconfianza matemática” y su relación con la “ansiedad matemática” en dos de los colegios técnicos de la provincia de Cartago (Tesis de licenciatura inédita). Instituto Tecnológico de Costa Rica.

Cea, M.A. (1999). Metodología cuantitativa: estrategias y técnicas de investigación social. Madrid: Síntesis.

Cerda, C., Ortega, R., Casas, J., Del Rey, R. y Pérez, C. (2016). Predisposición desfavorable hacia el aprendizaje de las Matemáticas: una propuesta para su medición. En: Estudios Pedagógicos XLII, No. 1: 53-63.

Cerda, G, Pérez, C; Aguilar, M y Aragón, E. (2018). Algunos factores asociados al desempeño académico en matemáticas y sus proyecciones en la formación docente1 Educação e Pesquisa, vol. 44, Faculdade de Educação da Universidade de São Paulo DOI: 10.1590/S1678-4634201706155233.

Cerda, G., Romera, E. M; Casas. J. A.; Pérez, C. y Ortega-Ruiz, R. (2017). Influencia de variables cognitivas y motivacionales en el rendimiento académico en matemáticas en estudiantes chilenos. Educación XX1, 20(2), 365-385, doi: 10.5944/educXX1.19052

Coto, J. (2018). Estudio de la relación entre la “autoconfianza matemática” y la “actitud hacia la utilidad de la matemática” en los estudiantes del tercer ciclo del Colegio de San Luis Gonzaga, Cartago, Costa Rica. (Tesis inédita de licenciatura) Instituto Tecnológico de Costa Rica.

Del Río, M., Strasser, K., y Susperreguy, M. (2016). ¿Son las habilidades matemáticas un asunto de Género? Los estereotipos de género acerca de las matemáticas en niños y niñas de Kínder, sus familias y educadoras. Calidad en la Educación, 45, 20-53.

Fennema, E. y Sherman, J. A. (1976). Fennema-Sherman mathematics attitude scales. Instruments designed to measure attitudes toward the learning of mathematics by males and females. JSAS Catalog of Selected Documents of Psychology, 6(31).

Frías-Navarro, D. y Pascual, M. (2012). Prácticas del Análisis Factorial Exploratorio (AFE) en la investigación sobre Conducta del consumidor y marketing. Suma Psicológica, Vol. 19, Núm. 1, pp. 45-58 Recuperado de: https://www.uv.es/~friasnav/FriasNavarroMarcopsSoler.pdf

Gamboa, R. (2012). ¿Equidad de género en la enseñanza de las Matemáticas? Revista Electrónica Educare, 16(1).

Gil, N., Blanco, L. & Guerrero, E. (2005). El dominio afectivo en el aprendizaje de las matemáticas. Una revisión de sus descriptores básicos. UNIÓN, 2, 15-32.

Gil, N., Blanco, L. & Guerrero, E. (2006a). El dominio afectivo en el aprendizaje de las matemáticas. Revista Electrónica de Investigación Psicoeducativa, 4(1), 47-72. Recuperado de http://www.investigacion-psicopedagogica.org/revista/articulos/8/espannol/Art_8_96. pdf

Gil, N., Blanco, L. y Guerrero, B. (2006b). El papel de la afectividad en la resolución de problemas matemáticos. Revista de educación, (340), 551-569.Recuperado de: http://dialnet.unirioja.es/servlet/articulo?codigo=2100483

Gómez-Chacón, I. (2007). Sistema de creencias sobre las matemáticas en alumnos de secundaria. Revista Complutense en Educación, 18 (2), 125-143.

Gómez-Chacón, I. (2010). Actitudes de los estudiantes en el aprendizaje de la matemática con tecnología. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 28(2), 227–244. https://www.raco.cat/index.php/Ensenanza/article/view/199615.

Guven, B. & Cabakcor, B. (2013). Factors influencing mathematical problem- solving achievement of seventh grade Turkish students. Learning and Individual Differences, 23, 131-137.

Hailikari, T., Nevgi, A., & Komulainen, E. (2008). Academic self-beliefs and prior knowledge as predictors of student achievement in Mathematics: A structural model. Educational Psychology, 28(1), 59-71.

Hidalgo, S., Maroto, A., y Palacios, A. (2004). ¿Por qué se rechazan las matemáticas? Análisis evolutivo y multivariante de actitudes relevantes hacia las matemáticas. Revista de Educación, 334, 75-95.

Jiménez, K. y Montero, E. (2013). Aplicación del modelo de Rasch, en el análisis psicométrico de una prueba de diagnóstico en matemática. Revista digital Matemática, Educación e Internet, 13(1), 1-23.

Lozano, L. & de la Fuente- Solana, E. (2013). Diseño y validación de cuestionarios. En Pantoja-Vallejo. En Manual básico para la realización de tesinas, tesis y trabajos de investigación. España: Editorial EOS (pp. 251-274).

Marchand, G., & Skinner, E. A. (2007). Motivational dynamics of children’s academic help-seeking and concealment. Journal of Educational Psychology, 99(1), 65-82. doi: 10.1037/0022-0663.99.1.65

Meza, G., Agüero, E., & Suárez, Z. (2019). La autoconfianza matemática de estudiantes de educación secundaria: Un estudio en Costa Rica. Revista Electrónica Educare, 23(1), 1-15. https://doi.org/10.15359/ree.23-1.3

Meza, G., Suárez, Z., Agüero, E. (2016). ESACEM: estudio de la autoconfianza matemática en estudiantes de educación media. Informe Final, http://test.tec.ac.cr/proyectos/esacem

Ministerio de Educación Pública. (2012). Programas de estudio de matemáticas. San José,Costa Rica: MEP.

Moenikia, M. & Zahed-Babelan, A. (2010). A study of simple and multiple relations between mathematics attitude, academic motivation and intelligence quotient with mathematics achievement. Social and Behavioral Sciences, 2, 1537-1542. doi:10.1016/j. sbspro.2010.03.231.

Morales, A. & Arce, C. (2017). Estudio de la relación entre la ansiedad matemática, la autoconfianza matemática y la actitud hacia la utilidad de la matemática en estudiantes de Ciencias de la Salud de una universidad privada de Costa Rica (Tesis de licenciatura). Instituto Tecnológico de Costa Rica.

Morales-Vallejo, P. (2012). El tamaño del efecto (effect size): análisis complementarios al contraste de medias. Recuperado de: https://web.upcomillas.es/personal/peter/investigacion/Tama%f1oDelEfecto.pdf

Muñoz, J. M. y Mato, MD. (2006). Diseño y validación en un cuestionario para medir las actitudes hacia las matemáticas en alumnos de ESO. Revista galego-portuguesa de psicoloxía e educación: revista de estudios e investigación en psicología y educación, 13, pp. 413-424.

Pérez-Tyteca, P. (2012). La ansiedad matemática como centro de un modelo causal predictivo de la elección de carreras. (Tesis Doctoral). Universidad de Granada. Recuperado de: http://hera.ugr.es/tesisugr/2108144x.pdf

Pérez-Tyteca, P., Monje, J., & Castro, E. (2013). Afecto y matemáticas. Diseño de una entrevista para acceder a los sentimientos de alumnos adolescentes. Avances de Investigación en Educación Matemática. No 4. 65- 82. Sociedad Española de Investigación en Educación Matemática (SEIEM).

Ramos, N. (2015). Estudio de la relación entre "Ansiedad Matemática" y "Autoconfianza Matemática" en tres colegios privados costarricenses. (Tesis de licenciatura inédita) Instituto Tecnológico de Costa Rica.

Sánchez, J. & Jiménez, A. (2016). Estudio de la relación entre las variables de autoconfianza matemática y autoestima en estudiantes de la Sede Interuniversitaria de Alajuela (UCR - UNA - ITCR) (Tesis de licenciatura). Instituto Tecnológico de Costa Rica.

Skaalvik, S., & Skaalvik, E. M. (2005). Self-concept, motivational orientation, and help-seeking behavior in mathematics: A study of adults returning to high school. Social Psychology of Education, 8(3), 285302. doi.org/10.1007/s11218-005-3276-3

Vega, A. (2017). Estudio de la relación entre la “ansiedad matemática”, la “autoconfianza matemática” y la “percepción de la utilidad de la matemática” en estudiantes de una universidad privada de Costa Rica (Tesis de licenciatura). Instituto Tecnológico de Costa Rica.

Wynta, R. & López, V. (2017). Estudio de los niveles de “ansiedad matemática” y “autoconfianza matemática” que manifiestan los estudiantes de la Universidad de Costa Rica, Sede del Caribe (Tesis de licenciatura). Instituto Tecnológico de Costa Rica.

Yaratan, H., & Kasapoğlu, L. (2012). Eight grade students’ attitude, anxiety, and achievement pertaining to mathematics lessons. Social and Behavioral Sciences 46, 162-171. doi: 10.1016/j.sbspro.2012.05.08.

---