Simulación numérica con MATLAB y modelos Probit para calcular las consecuencias por daño pulmonar de explosiones en calderas

Numerical simulation with MATLAB and Probit models to calculate the consequences due to lung damage from boiler explosions

Ricardo A. Morales-Vargas1

Fecha de recepción: 15 de enero, 2024
Fecha de aprobación: 27 de abril, 2024

Morales-Vargas, R Simulación numérica con MATLAB y modelos Probit para calcular las consecuencias por daño pulmonar de explosiones en calderas. Tecnología en Marcha. Vol. 38, No 1. Enero-Marzo, 2025. Pág. 44-58.

https://doi.org/10.18845/tm.v38i1.7022

Palabras clave

Calderas; explosión; evaluación de riesgos; análisis de riesgo; riesgos; regulación; efectos domino; herramientas computacionales; simulación.

Resumen

Las explosiones de calderas generan graves daños en instalaciones de trabajo así como lesiones a los operadores, que pueden ir desde quemaduras y laceraciones hasta la muerte, con altos costes económicos para las empresas usuarias. En entornos industriales como institucionales, la principal causa de las explosiones de las calderas es el bajo nivel de agua, generándose sobrecalentamiento de los tubos de las calderas, vaporización repentina, aumento de la presión y fallas catastróficas. A pesar de estos riesgos, existen escasas herramientas computacionales para calcular sus consecuencias. Prevenir este tipo de accidentes es fundamental en la industria, comercio y servicios ya que éstos deben ser intrínsecamente seguros para cumplir su misión económica y humanitaria, respectivamente. Este artículo revisa los requisitos técnicos para el funcionamiento seguro de las calderas centrándose en la ubicación correcta y el distanciamiento de la sala de calderas para minimizar el efecto dominó y lesiones humanas. Se desarrolló un script y código compilado en el entorno MATLAB® para calcular la sobrepresión máxima resultante en función de la distancia, con parámetros ingresados por el usuario para una variedad de calderas y condiciones de explosión. El daño de la onda de choque se estimó mediante cálculos Probit considerando el daño pulmonar, para facilitar el análisis y recomendar la ubicación ideal o mejorada de la sala o compartimento de calderas. Se concluye que la normativa deba incluir un análisis obligatorio de consecuencias, utilizando modelos numéricos para guiar la distribución de las plantas y proteger a los trabajadores y vecinos ante las explosiones.

Keywords

Boilers, explosions; risk assessment; risk analysis; risks; regulation; domino effects; computing tools; simulation.

Abstract

Boiler explosions around the world cause serious damage to work facilities as well as injuries to operators, which can range from burns and lacerations to death, with high economic costs for user companies. In industrial and institutional environments, the main cause of boiler explosions is low water level, which causes boiler tube overheating, sudden vaporization, pressure rise, and catastrophic failure. Despite these risks, there are few computational tools to calculate their consequences. Preventing this type of accident is essential in industry and commerce, as well as the service sectors since these must be intrinsically safe to fulfill their economic and humanitarian mission, respectively. This article reviews the technical requirements for safe operation of boilers focusing on correct location and distancing from the boiler room to minimize the domino effect and human injuries. The author developed a script and compiled code in the MATLAB® environment to calculate the resulting maximum overpressure as a function of distance, with user-entered parameters for a variety of boilers and explosion conditions. Shock wave damage was estimated using Probit calculations considering lung damage, to facilitate analysis and recommend the ideal or improved location of the boiler room or compartment. It is concluded that regulations must include a mandatory analysis of consequences, using similar or more elaborate numerical models, to guide the distribution of plants and protect workers and neighbors from explosion overpressure effects.

Introducción

Las calderas, independientemente del tipo de combustible utilizado, normalmente funcionan a altas presiones y temperaturas, lo que presenta riesgos importantes para los operadores, el resto del personal de la planta y los equipos vulnerables al efecto dominó. Es necesario contar con un estricto marco de seguridad durante todo su ciclo de vida, comenzando por la ubicación del proyecto y distanciamiento de las operaciones críticas de la sala de calderas, construcción del cuarto de calderas, la instalación y puesta en servicio, así como capacitación, procedimientos de operación, mantenimiento, inspección, almacenamiento y desmantelamiento de los equipos. De ahí que resulte de primordial importancia planificar la adecuada ubicación de las calderas y analizar los principales riesgos que pueden generar (explosión de la caldera y propagación de ondas expansivas) mediante técnicas apropiadas de simulación numérica, tal y como han propuesto varios autores [1- 3].

Como lo analizó el autor en un trabajo anterior [4], esto desafortunadamente no ha encontrado resonancia en la comunidad reguladora, y la ubicación de la caldera rara vez se guía por un estricto análisis de riesgo respaldado por cálculos de ingeniería. Ese trabajo analizó las regulaciones de varios países de habla hispana, entre ellos Perú, México, España, Chile, Colombia y Costa Rica, así como las de Estados Unidos y Nueva Zelanda. En los países latinoamericanos los riesgos por explosión o sobrepresión no están específicamente considerados en los requisitos de instalación, para orientar el espaciamiento o la resistencia estructural de las edificaciones que los contienen. La mayoría de estos instrumentos legales se limitan a referencias genéricas sobre la ventilación, la resistencia al fuego de los muros, indicaciones generales para el uso del código sísmico de cada nación y aspectos básicos de higiene y salud ocupacional. Si bien las normas favorecen el funcionamiento seguro, no se centran en los mayores riesgos que presentan dichos equipos, como los daños por sobrepresión o el impulso energético de los materiales proyectados.

Una publicación de la industria del petróleo y gas [5] dirigida al sector de procesos químicos establece una serie de nomogramas y tablas para la separación de diferentes secciones de dichas operaciones e indica que los “utilities” deben estar a 15 metros de los centros de control eléctrico, salas de máquinas, sistemas de protección contra incendios y otros edificios de servicios; a 30 metros de equipos peligrosos (compresores, salas de control, estaciones de bombeo y otras unidades de proceso) y a 100 metros de tanques presurizados o refrigerados. Específicamente para tanques a presión atmosférica, como lo ejemplifican los tanques de almacenamiento de combustible para calderas, recomienda 75 metros entre éstos y las áreas de servicios generales donde se ubican las calderas y sus equipos auxiliares. Sin embargo, se hace hincapié en la protección de los activos de las empresas, con el objetivo de evitar la cadena de acontecimientos (efecto dominó), pero el documento no proporciona detalles sobre cómo se arribó a a estas distancias.

Sólo el reglamento español del año 2021 sobre calderas y recipientes a presión [6] indica pautas para la clasificación y ubicación de las calderas en función de parámetros energéticos, pero las distancias requeridas a paredes, linderos y otros equipos son bajas en comparación con los posibles riesgos [4].

Los datos tabulados por varias agencias [7] indican que las fallas en las calderas tienen una frecuencia de 0,9 a 4,0 fallas/año, lo que limita la seguridad y confiabilidad. Las fallas en los controladores de nivel ocurren a una tasa de entre 0,03 y 2,0 fallas/año y las fallas en las válvulas de alivio se estiman en 0,03-0,08 fallas/año. Estos aspectos, que contribuyen a la falla catastrófica de las calderas, adquieren una importancia crítica cuando se trata de equipos para generación de energía térmica/eléctrica, cuyas presiones son aún mayores [1] o en entornos institucionales donde la continuidad y confiabilidad de la operación es crítica.

Existen numerosos ejemplos de explosiones de calderas, debidas principalmente a bajos niveles de agua. La investigación y el análisis de estos accidentes ha sido una práctica común en la ingeniería desde el comienzo de la revolución industrial [8], una práctica que sigue siendo de importancia en la actualidad. Los datos estadísticos publicados por la Junta Nacional de Inspectores de Calderas y Recipientes a Presión para el año 2002 [9], indican que el 85% de los accidentes son atribuibles a dos causas; bajo nivel de agua (49%); y error en la operación o mal mantenimiento (36%). Los accidentes asociados con deficiencias de diseño y fabricación, fallas de control y quemadores, instalación inadecuada, fallas de válvulas de seguridad y reparaciones inadecuadas tienen tasas de falla más bajas; pero aun así es necesario abordarlos. Entre 1992 y 2001, hubo un promedio de 2.334 accidentes/año, que resultaron en 127 muertes. El número medio de heridos es de 1 cada 32 accidentes [10]. En 2002, hubo 1.487 accidentes en calderas de generación de energía, vapor y agua caliente, causando 16 heridos y 3 muertes sólo en los EE.UU [9].

La otra causa común de explosiones se origina en el lado del fuego, debido a la acumulación de combustible en los tubos, y la liberación repentina de la energía de la combustión, pero generalmente causando solo daños internos a la caldera, el hogar, tubos, ladrillos refractarios; pero sin exceder los límites mecánicos y materiales de los equipos que contienen presión del lado del agua, por lo que no son analizados en este estudio.

Publicaciones de la Sociedad Americana de Ingenieros de Energía [11] y del Estado de Tennessee [12] citan la explosión de 2007 en una caldera modelo 2000 CB que operaba a 150 psi, que causó lesiones graves a un operador, destruyendo una pared de la sala de calderas, provocando que el equipo se desplazara unos 30 metros hacia otra zona de la planta, que quedó destruida. La puerta trasera de la caldera también salió despedida a casi 30 metros de la planta dañando varios coches en un aparcamiento cercano. El análisis del accidente indicó que durante la operación con poca agua, se introdujo agua de alimentación fría que repentinamente se vaporizó causando una sobrepresión destructiva [11, 12]. En América Latina, durante el primer semestre de 2020 se reportaron 9 accidentes, con un muerto y 12 heridos [13]. Más recientemente, un accidente de caldera en una planta pesquera en Manta (Ecuador) dejó 3 muertos y 7 heridos [14]. Un estudio de Guimaraes et al [15] deja ver que en Brasil, entre el año 2002 y el 2020 se investigó por el Estado un total de 70 accidentes, con un total de 72 víctimas fatales, siendo el sector de fabricación de alimentos y bebidas el más afectado.

Los modelos de consecuencias habituales para este tipo de accidentes, en cuanto a consecuencias humanas y de equipos, corresponden a los modelos BLEVE; una expansión isentrópica, cercana a la presión atmosférica; que se han utilizado a lo largo de los años [2,3,4,16-20]. En estos, la energía del sistema se expresa como equivalente de TNT. Luego, la sobrepresión se puede calcular utilizando correlaciones de distancia normalizada[19, 21-23] junto con modelos Probit para estimar la probabilidad de sufrir consecuencias debido a diferentes efectos, como, hemorragia pulmonar, rotura de tímpanos, daños oculares y daños por impactos de fragmentos [7, 16, 17, 24-27], siendo el daño pulmonar el predominante [28]. Dicho daño se caracteriza por ruptura de los alveolos, sangrado intra-parenquimal, seguido de edema y compromiso respiratorio que puede llevar a la muerte [29], por la dificultad del tratamiento de la inflamación, hemorragia, tratamiento coagulante y trombosis.[30].

Más recientemente estos estudios se han combinado con modelos computacionales para dinámica de fluidos y modelos numéricos para análisis estructural [2, 26-27, 32], que han permitido modelar el efecto rebote o “dominó” [16, 33, 34], ayudando a optimizar la disposición de la planta [4, 35]. Las explosiones de calderas en hospitales e industrias se han estudiado con software numéricamente complejo como LS-DYNA, un programa basado en análisis estructural de elementos finitos [2]. Otros softwares, como PHAST y CHEMCAD, se pueden utilizar para simular muchos problemas de ingeniería que requieren datos termodinámicos y se han utilizado para analizar explosiones de calderas y sus consecuencias [3]. MATLAB se ha utilizado en entornos de enseñanza y en muchos entornos industriales para simular problemas de ingeniería, pero pocas referencias apuntan a MATLAB para calcular las consecuencias de una explosión de calderas [35].

Este artículo describe la implementación de una estrategia guiada por el usuario en MATLAB para analizar las consecuencias de las explosiones para una variedad de tamaños de calderas y guiar la ubicación segura durante la planificación del sitio. Se centra en las consecuencias para las poblaciones humanas y los trabajadores, utilizando la probabilidad de hemorragia pulmonar como criterio de valoración, indicador que se encuentra comúnmente en la literatura [19, 24, 25]. Este análisis y la herramienta computacional propuesta esperan llenar un vacío en las regulaciones de calderas de los países latinoamericanos y de habla inglesa, que tienen muy pocas recomendaciones para su ubicación basadas en consideraciones de energía y explosividad.

Metodología

Los cálculos que se describen a continuación fueron implementados en MATLAB R2023a, bajo licencia a la Universidad de Costa Rica. El programa calcula la energía de explosión de una caldera, para facilitar al usuario un correcto diseño de la planta. El software le solicita información al usuario en inglés o español. El software recibe los datos estimados de presión de estallido, presión atmosférica y solicita al usuario el rango de tamaños de caldera a estudiar en m3 de agua líquida.

Aunque el software solicita dicho dato al usuario, el espacio libre de vapor, puede estimarse en un 10% del volumen del líquido, algo común en la mayoría de las calderas pirotubulares, de las más utilizadas en Latinoamérica y en Costa Rica. Lo anterior considerando la información de los modelos CB de empresa Cleaver-Brooks, fabricante y líder en diseño a nivel internacional, emulado por otras empresas. La sobrepresión para la gama de calderas estudiadas se representa en función de la distancia y su equivalente de TNT en kilogramos, TNT (eq). La Tabla 1 muestra tamaños de caldera típicos en el mercado, que pueden utilizarse por el usuario para guiar la ubicación de éstas, aplicando el software MATLAB propuesto. La clase de caldera corresponde a la clasificación de los equipos según el Decreto 26789-S-MTSS, Reglamento de Calderas de Costa Rica.

Cuadro 1. Tipo de caldera y volúmenes de líquido/vapor

Caso (Clase de Caldera)	Potencia de Caldera (HP)	Generación de vapor (kg/hr)	Volumen líquido normal (m3)	Volumen vapor (m3)
1 (D)*	4	62	0,06	0,006
2 (C)	50	780	1,42	0,178
3 (C)	125	1950	2,61	0,261
4 (B)	200	3120	3,85	0,385
5 (B)	300	4680	5,80	0,580
6 (B)	400	6240	6,97	0,697
7 (A)	600	9360	10,46	1,046
8 (A)	800	12480	12,41	1,241

* Nota: Este caso corresponde a promedios de otros fabricantes, ya que el fabricante líder no trabaja en el rango bajo de la escala.

Luego, el programa solicita al usuario que especifique el número de índice del tamaño de caldera deseado en el que desea centrar su análisis y muestra un gráfico similar y menos poblado de sobrepresión versus distancia y un gráfico de sobrepresión versus el valor Probit para el riesgo. Luego se muestra una tabla Probit para estimar el % de daño a la población expuesta, en este caso, el % de mortalidad por hemorragia de pulmón.

La explosión de la caldera se modeló como una expansión isentrópica de vapor que causa ruptura dúctil [4, 19-24]. La energía liberada durante una expansión isentrópica de un gas ideal se expresa según la ecuación 1 de la termodinámica:

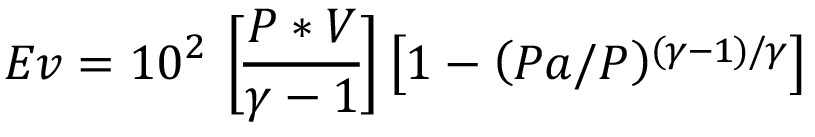(1)

donde,

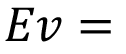Energía liberada por la expansion del vapor (kJ)

P = Presión dentro el recipiente al momento de la explosion (bar)

V = Volumen inicial de vapor (m3)

Pa = Presión atmosférica(bar)

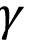= Cp/Cv del vapor, y

Cp = calor específico a presión constante

Cv = calor específico a volume constante

Posteriormente se calculó la masa equivalente de TNT para esta energía, lo que permite utilizar las ecuaciones y nomogramas de distancia normalizada (dn) y sobrepresión desarrollados por varios autores [19, 36-38]. Para el presente estudio, y para eliminar sesgos y dificultades en la lectura de nomogramas, se utilizó la ecuación empírica propuesta por Kinney & Graham citada por Birk [36].

La masa, W(TNT), de TNT equivalente (kg), según Casal et al [19, 24] se calculó con la ecuación 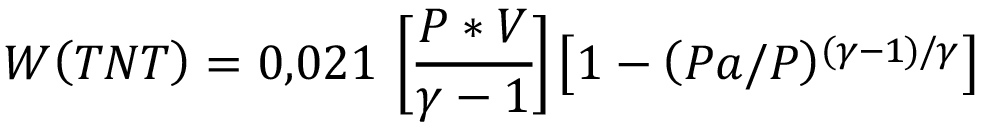2:

(2)

Como describen Casal et al, si el recipiente también contiene líquido sobrecalentado, como en el caso de una explosión isentrópica, la masa de líquido se vaporizará repentinamente al contactar la atmósfera y el volumen que ocuparía este líquido vaporizado debe calcularse a la presión de vapor en el recipiente justo antes de la explosión, sumando este volumen virtual al volumen de vapor real [19]. Así, la masa equivalente de TNT será:

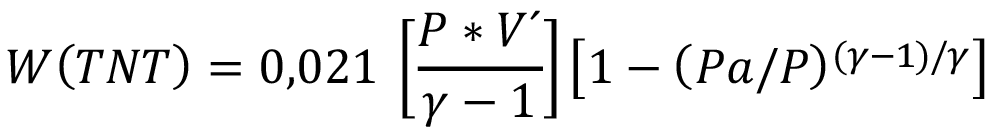(3)

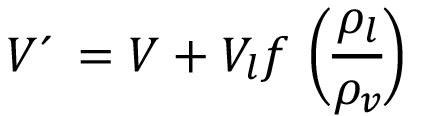(4)

donde V es el volumen de vapor en la caldera, 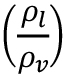es la relación entre la densidad del líquido y el vapor, 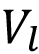es el volume del líquido y f, es la fracción vaporizada (flasheo),

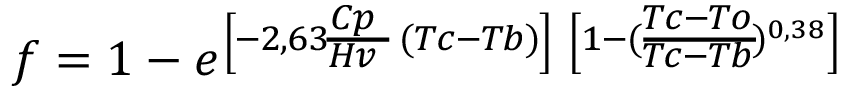(5)

y,

Hv = Entalpía de vaporización (kJ/kg)

Tc = Temperatura crítica (K)

Tb = Temperatura de ebullición a la presión atmosférica (K)

To = Temperatura en el recipiente al momento de la explosion (K)

e = 2.71828

La distancia normalizada dn viene dada por la siguiente ecuación, donde d es la distancia desde el centro de la explosión a la que se estima la sobrepresión, y B es la fracción de la energía que se transforma en una onda de presión, que para los efectps de este estudio, se estimó en un 40% para una fractura dúctil [19]. En el caso de fractura frágil, este valor es aproximadamente un 80%, como proponen Casal et al [19]. Sochet [39] por su parte establece que se da un rendimiento de la explosion que puede rondar entre 0,4 y 0,9. El software, no obstante, permite al usuario indicar este valor. Este aspecto debe analizarse claramente, ya que las calderas pueden estar sujetas a altas variaciones de pH que pueden provocar fracturas frágiles [40] (ej. fragilización cáustica).

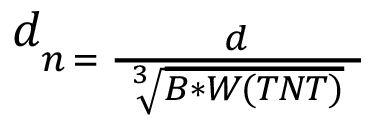(6)

La sobrepresión se calculó para cada distancia d (distancia real) utilizando la ecuación empírica propuesta por otros autores [20, 22, 41], aplicable para explosiones BLEVE en el rango medio y para tanques a presión, respectivamente, en base a su equivalente en TNT:

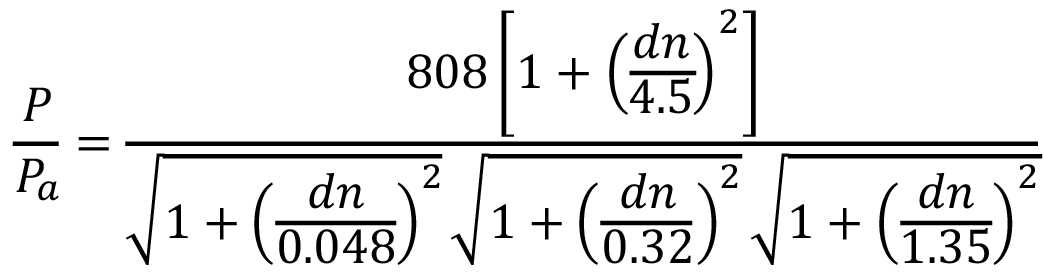(7)

donde:

P = Sobrepresión generada por la explosión (bar)

Pa = presión atmosférica (bar)

dn = distancia normalizada (m/kg1/3)

Las propiedades físicas del vapor se calcularon en MATLAB utilizando las ecuaciones para correlaciones de temperatura y presión reducidas presentadas por Affandi et al [42].

Los daños esperados por sobrepresión se implementaron numéricamente en MATLAB, utilizando las ecuaciones Probit propuestas por Hirsch, como lo discutió Casal para la hemorragia de pulmón [19, 24]. En el caso de daños materiales y equipos a las instalaciones se puede tomar como base el trabajo de diversos autores y resumido por Cozzani et al [43-45]. Se deben utilizar las ecuaciones Probit [17,19,24,35,44] con la tabla de equivalencia propuesta por Finney [45]. Las ecuaciones son de la forma:

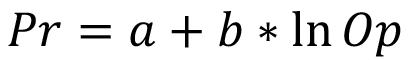
donde:

Pr = valor Probit (valor probabilístico del daño a la población expuesta)

a = constante que depende del tipo de lesión y tipo de carga de exposición

b = constante que depende del tipo de exposición

Op = variable que representa la carga de exposición (en este caso la sobrepresión e la explosion)

Según Finney, la variable dependiente Pr se define como una variable aleatoria según una distribución estadística normal con un valor medio de 5 y una desviación estándar de 1, lo que significa que Pr = 5 corresponde a un valor Probit del 50%. En este estudio se utilizó la ecuación Probit de Hirsch con parámetros para hemorragia pulmonar donde a= -77,1, b=6,91 y Op es la sobrepresión generada (N/m2).

Resultados

A modo de ejemplo, se utilizaron los parámetros de entrada al software MATLAB que se muestran en el cuadro 2 para generar las gráficas que se muestran en la figura 1.

Cuadro 2. Parámetros de entrada al software MATLAB.

Parámetro	Valor	Observaciones
Presión de ruptura	10 bar	Corresponde a 150 psi, presión máxima de operación usual en calderas (Costa Rica
Presión atmosférica	1 bar
Tamaño mínimo de caldera (volumen líquido)	1 m3	Volumen aproximado de una caldera de 50 HP
Tamaño máximo de caldera (volumen líquido)	6 m3	Volumen aproximado de una caldera de 300 HP
Número de calderas a graficar	4	Rango de 50-300 HP (Fig. 1)
Índice de caldera a analizar	2	Fig. 2
% de vapor en la caldera	10%	“Headspace” usual en calderas pirotubulares CB
% de energía liberado como onda de sopresión	40%	Ruptura dúctil

La Figura 1 muestra la salida de MATLAB en un gráfico log-log de la distancia versus la sobrepresión generada, para una variedad de calderas a las condiciones definidas por el usuario: presión de ruptura, presión atmosférica y rango de volumen de líquido y de vapor de la caldera, % de vapor en la caldera y el % de energía incorporado a la onda de sobrepresión. A partir de estos datos se calcula la masa equivalente de TNT como muestra el cuadro de leyenda de la gráfica.

Figura 1. Salida de MATLAB No. 1.

Como se menciona en la sección de metodología, el programa luego solicita un número de índice para el gráfico en el que el usuario desea enfocarse y proporciona una vista menos poblada en formato log-log para facilitar la inspección de la gráfica por el usuario (Figura 2).

Figura 2. Salida de MATLAB No. 2.

Los parámetros Probit predeterminados para la hemorragia de pulmón se utilizan para generar un gráfico semilogarítmico de sobrepresión versus los valores Probit, como se muestra en la Figura 3.

Figura 3. Salida de MATLAB No. 3.

Luego, el programa muestra la tabla de valores probit de Finney (Figura 4), que se utiliza para estimar el % de población afectada en las sobrepresiones de interés, y correspondientes al valor Probit leídos de la Figura 3.

Figura 4. Salida de MATLAB No. 4. Fuente: https://biocomm.eu/2019/04/03/guide-to-essential-biostatistics-i-the-scientific-method-probit/ (Cited: 27-6-2022).

El resultado completo del programa MATLAB R2023a desarrollado se muestra en la Figura 5, que incorpora en una sola ventana las cuatro salidas gráficas simultáneamente. La versión compilada está disponible previa solicitud al autor.

Figura 5. Salida completa del MATLAB No. 5.

Discusión

Las regulaciones nacionales generalmente incorporan especificaciones de fabricación y operación de los equipos, pero omiten requisitos sobre distanciamiento entre salas o compartimentos de calderas y otras exposiciones [4], ignorando los efectos de una sobrepresión en caso de un accidente mayor. El modelo numérico y el procedimiento propuesto permiten a los diseñadores de plantas llegar a “distancias seguras” entre la caldera y otros equipos o exposiciones humanas en caso de falla catastrófica, lo que limita los efectos de la onda expansiva y puede guiar los esfuerzos regulatorios.

Las distancias de seguridad sugeridas determinadas a partir de la salida del software y la ayuda de la tabla Probit de Finney deben considerarse un mínimo de cumplimiento en instalaciones industriales, ya que existen discrepancias entre autores [3, 18, 19] en cuanto a la proporción de la expansión. energía que se transforma efectivamente en una onda de sobrepresión.

El presente estudio se centró en los cálculos de sobrepresión generada por una caldera de vapor BLEVE y no incorpora la energía utilizada en la proyección de fragmentos y sus efectos probabilísticos, que podrían ser de importancia [24]. El resultado del software considera la ruptura dúctil, en la que se supone que el 40% de la energía liberada se transforma en una onda de sobrepresión, lo cual debe verificarse en cada caso, ya que dentro de altas presiones podrían existir otro tipo de condiciones (i.e. fragilización cáustica, en calderas que funcionan a un pH muy alcalino [40].

El autor coincide con el criterio de Sochet [39] de que los modelos utilizados en el presente estudio representan una opción simple y económica, en comparación con los modelos computacionales de dinámica de fluidos u otros modelos numéricos para el análisis estructural de edificios [2,3], ya que estos últimos requieren mayores capacidades computacionales y experiencia del usuario. Dichas aplicaciones también pueden requerir datos estadísticos sobre las condiciones meteorológicas para la simulación, que no siempre están disponibles en todas las instalaciones industriales. Asimismo, dicho análisis podría ser complicado de implementar al considerar los efectos del suelo, las paredes y las aberturas de ventilación o de entrada/salida, así como otros equipos cercanos, lo que solo es possible con software de elementos o diferencias finitas para mecánica de fluidos, con altos requerimientos computacionales.

El software MATLAB desarrollado es fácil de adaptar a otras condiciones que pueden merecer exploración, como valores distintos para la proporción de energía incorporada en la onda expansiva, diferentes proporciones de líquido a vapor en el recipiente y ofrece la ventaja de explorar diferentes tamaños de calderas simultáneamente. La presión de ruptura se ingresa por el usuario, de modo que se podrían utilizar diferentes criterios, como límites operativos o estructurales, para simular la explosión de diferentes tamaños de calderas, en especial ya que en accidentes reales la presión de ruptura es superior a la presión de operación usual.

El criterio de valoración utilizado, la hemorragia de pulmón (0,7-0,9 bar), tomado de Sajja et al [48], es similar al rango en el que se observan la mayoría de los daños serios en los edificios (cuadro 3). El valor anterior y las distancias correspondientes determinadas a partir de los resultados gráficos podrían ser indicativos de la dimensión más corta que debe tener un cuarto de calderas para minimizar la exposición del resto del personal de la planta. El cuadro 3 muestra el daño esperado a personal e instalaciones, tomado de Lees y otros autores [14, 48], Los valores coloreados son los límites umbral recomendados por Fang [3] para el análisis. Si fuera necesario analizar diferentes criterios de valoración citados en la literatura [17,23,44,47], esto se puede implementar fácilmente cambiando dos parámetros en el código MATLAB (parámetros Probit a y b), y cambios menores en los títulos de salida gráfica programados.

Cuadro 3. Daños esperados según sobrepresión (bar).

Daños esperados	Sobrepresión
	(bar)
Ruido fuerte (143 db), “boom sónico”, ruptura de vidrios	0,0028
Presión típica para ruptura de vidrios	0,0103
Daño estructural menor y limitado	0,0300
Ventanas generalmente rotas, algún daño a marcos de ventanas.	0,0345-0,0690
Daño menor a estructuras domésticas	0,0483
Demolición parcial de casas; tornándolas inhabitables	0,0690
Paneles metálicos corrugados fallan y se tuercen. Paneles de madera en casas son derribados	0,0690-0,1379
Rango para heridas por laceración, de leves a serias, por vidrio volante y otros proyectiles.	0,0690-0,5517
Colapso parcial de paredes y techos de casas	0,1379
Concreto no reforzado o paredes de ladrillo se rompen	0,1379-0,2069
Rango para probabilidad del 1 al 90% de ruptura de tímpanos en poblaciones expuestas	0,1655-0,8414
50% destrucción de paredes de ladrillo en casas	0,1724
Marcos de acero en edificios sufren distorsión y son separados de su fundación	0,2069
Postes de madera rotos.	0,3448
Casi completa destrucción de casas	0,3448-0,4828
Vuelco de vagones de tren cargados	0,4828
Demolición de vagones de carga en trenes	0,6207
Probable destrucción total de edificios	0,6897
Daño hemorrágico en pulmones, contusiones, desorientación	0,7-0,9
1-10% de población con daño hemorrágico en pulmones	1.02-1.2
1-99% de fatalidades (muertes) en poblaciones expuestas por efectos directos de la explosión	1,0-2,0

Adaptado de: Lees, Frank P. 1980. Loss Prevention in the Process Industries, Vol. 1. London and Boston: Butterworths y Fang et al, 2012; Sajja et al, 2020.

MATLAB, como herramienta computacional, es fácil de aprender, está bien documentado y se utiliza en las ciencias y la ingeniería, contando con comunidades de apoyo en línea. La utilidad y facilidad de implementación del modelo numérico propuesto y las capacidades gráficas del software, permiten a los reguladores incentivar el cumplimiento de un adecuado análisis de riesgos antes de la instalación de la caldera Los diseñadores, organizaciones profesionales y usuarios de calderas en todos los sectores económicos pueden beneficiarse de este análisis, que sin duda puede contribuir a la reducción de accidentes y pérdidas económicas y humanas de forma significativa. En relación a lo anterior, se compartió el software utilizado y producto de una publicación previa [49] con una empresa consultora de ingeniería [50] que lo utilizaría para informar las decisiones de su cliente sobre ubicación de planta y posicionamiento de la caldera y su cuarto de control dentro de una instalación europea que suministra equipo de defensa.

Es necesario señalar que los accidentes descritos tienen el potencial de volverse más costosos para empresas y gobiernos si los trabajadores o las poblaciones cercanas ponen en marcha procesos legales de responsabilidad civil u otros procedimientos judiciales, lo que hace que la prevención a través del análisis de riesgos, el distanciamiento de las calderas y una mejor construcción sea una inversion provechosa para la economía y la sociedad en general, aspect que debe retomarse en la elaboración de la normativa internacional.

Referencias

[1] Shrivastava R, Patel P. Hazards Identification and Risk Assessment in Thermal Power Plant, International Journal of Engineering Research and Technology. 2014; 3(4): 17-37.

[2] Ibrahim MF, El-Arabaty HA, Moharran I. Effect of steam boiler explosion on boiler room and adjacent building’s structure. International Journal of Engineering Science and Invention. 2019; Vol. 8, No. 02, Series II: 17-37.

[3] Fang Q, Zhe Z, Qingmin S. Application of Phast in the Quantitative Consequence Analysis for the Boiler BLEVE. En: ISDEA ‘13: Proceedings of the 2013 Third International Conference on Intelligent System Design and Engineering Applications; 2013. pp. 369-372 https://doi.org/10.1109/ISDEA.2012.92

[4] Morales-Vargas RA. Simulación numérica de explosiones en calderas: Pautas para la distribución de planta como medida de mitigación de daños. Rev. salud ambient. 2020; 20(2):137-149.

[5] Global Asset Protection Services LLC, Oil and Chemical Plant Layout and Spacing, GAPS Guidelines, GAP 2.5.2, 2015.

[6] Real Decreto 809/2021, de 21 de septiembre, por el que se aprueba el Reglamento de equipos a presión y sus instrucciones técnicas complementarias. https://www.boe.es/boe/dias/2021/10/11/pdfs/BOE-A-2021-16407.pdf

[7] Creus A. Fiabilidad y Seguridad: Su aplicación en procesos industriales. Marcombo. Barcelona, 1992

[8] Scientific American, “Cause of Boiler Explosions” Scientific American 3, 25new, 386 (December 1860) doi:10.1038/scientificamerican12151860-386: https://www.scientificamerican.com/article/cause-of-boiler-explosions/ [consultado:Julio 6, 2022, 3:00 pm].

[9] National Board of Boiler and Pressure Vessel Inspectors, 2002 Incident Report, Bulletin. 2003; 58(2): 2-3

[10] National Board of Boiler and Pressure Vessel Inspectors, 2002 Boiler accidents report: To err is human, Bulletin, 2002; Vol. 57, No. 2. https://www.achrnews.com/articles/87615-boiler-accident-reports-to-err-is-human. [consultado:Julio 6, 2022, 3:00 pm].

[11] American Society of Power Engineers. Your Boiler Room a Time Bomb?: https://asope.org/sites/default/files/Documents/Your_Boiler_Room-A%20_Time_Bomb-2.pdf [Consultado: Julio 6, 2022, 3:10 pm].

[12] State of Tennessee (USA), 2007. Department of Labor and Workforce Development, Division of Boiler And Elevator Inspection. Boiler Accident Dana Corporation, Paris Extrusion Plant. https://www.ipe.org/docs/default-source/ontario-pdfs/incidents/ftsm-boiler-accident-with-pictures.pdf?sfvrsn=16821ed1_2 [Consultado: Julio 7, 2022, 3:16 pm].

[13] Editorial. Combustión, Energía y Ambiente. Relación de accidentes en el primer semestre, Calderas. Guía del Usuario en la Industria y el Comercio. CEACA, 2020 1(1), 6-8.

[14] El Universo, Sube a 3 la cifra de muertos por explosión en empresa atunera de Manta, (August 7th, 2020). Ecuador. https://www.eluniverso.com/noticias/2020/08/07/nota/7933896/explosion-empresa-atunera-manta-muertos/ (Consultado: Julio 5, 2022, 9:41 pm)

[15] Guimarães Landi R, Bandineli Montedo U, Netto Lahoz C,Using systems theory for additional risk detection in boiler explosions in Brazil, Safety Science, Volume 152, 2022,105761,ISSN 0925-7535.https://doi.org/10.1016/j.ssci.2022.105761.

[16] Cozzani V, Salzano B. The quantitative assessment of domino effects caused by overpressure Part I. Probit models, Journal of Hazardous Materials. 2004; A 107, 67-80.

[17] González-Ferradás E, Díaz-Alonso F, Sánchez-Pérez JF, Doval Miñarro M, Miñana-Aznar A, Ruiz-Gimeno J, Martínez-Alonso J. Consequence Analysis to Buildings from Bursting Cylindrical Vessels. Process Safety Progress, 2009; Vol. 28(2): 179-189.

[18] Lees FP. Loss Prevention in the Process Industries, Vol. 1, London and Boston: Butterworths. 1980.

[19] Casal J, Arnaldos J, Montiel H, Planas-Cuchi E, Vílchez JA. Modeling and Understanding BLEVEs (Chapter 22). In Handbook of Hazardous Materials Spills Technology: 22.1-22.27. http://aevnmont.free.fr/SACH-BOOKS/Petrochemistry/Handbook%20of%20Hazardous%20Materials%20Spills%20Technology/Part%20V.%20Spill%20Modeling/22.%20Modeling%20and%20Understanding%20BLEVEs.pdf [Consultado: Julio 6, 2022, 3:19 pm].

[20] Birk AM, Davison C, Cunningham M. Blast overpressures from medium scale BLEVE tests. Journal of Loss Prevention in the Process Industries. 2007; 20: 194-206.

[21] Díaz-Alonso F, González-Ferradás E, Sánchez-Pérez JF, Miñana- Aznar A, Ruiz-Gimeno J, Martínez-Alonso J. Characteristic overpressure-impulse-distance curves for the detonation of explosives, pyrotechnics or unstable substances. J Loss Prev Process Ind 2006; 19, 724-728.

[22] Van de Berg AC, Lannoy A. 1993. Methods for Vapor Cloud Explosion Blast Modelling. J. Hazard Mater 1993; 34, 151-171.

[23] González-Ferradás E, Díaz-Alonso F, Sánchez-Pérez JF, Miñana- Aznar A, Ruiz-Gimeno J, Martínez-Alonso J. Characteristic overpressure-impulse-distance curves for Vessel Burst. Process. Saf. Prog (AICHE) 2006; Vol, 25(3): 250-254.

[24] Casal J, Montiel H, Planas-Cuchi E, Vílchez JA. “BLEVE-bola de fuego” (Chapter 6). In: Análisis del riesgo en instalaciones industriales, Bogotá: Editorial Alfaomega; 2001. pp. 173-205.

[25] Instituto Nacional de Seguridad e Higiene del Trabajo (Ministerio de Trabajo y Asuntos Sociales de España, NTP 291: Modelos de vulnerabilidad de las personas por accidentes mayores: método Probit. https://www.cso.go.cr/legislacion/notas_tecnicas_preventivas_insht/NTP%20291%20-%20Modelos%20de%20vulnerabilidad%20de%20las%20personas%20por%20accidentes%20mayores%20metodo%20Probit.pdf. [Consultado: Julio 5, 2022, 3:22 pm].

[26] Zaghloul A, Ranaweera P, Mohotti D. Assessment of Blast Effects on Passengers in Underground Trains. En: 25th Australian Conference on Mechanics of Structures and Materials (ACMSM25) Brisbane, Australia; 2018.

[27] Kakogiannis D, Van Hemlrijck D, Wastiels J, Palanivelu S, Van Paepegem W, Vantomme J, Kotzakolios T, Kostopoulos V. Assessment of pressure waves generated by explosive loading. (preprint). Computer Modeling in Engineering and Sciences. 2010; 65(1): 1-15. https://www.researchgate.net/publication/228813743_Assessment_of_Pressure_Waves_Generated_by_Explosive_Loading. [Consultado: Julio 5, 2022, 3:24 pm]

[28] Scott TE, Kirkman E, Haque E, Mahoney P, Hardman JG. Primary blast lung injury - a review. British Journal of Anaesthesia, 2017; 118 (3): 311–6.

[29] Scott TE, Johnston A, Keene D, Rana M, Mahoney P. Primary Blast Lung Injury: The UK Military Experience. Military Medicine, 2020; 185, 5/6:e568.

[30] Li J, Zhang J, Shi M, Yu S, Ji M, Liang Y, Meng X. Crosstalk between Inflammation and Hemorrhage/Coagulation Disorders in Primary Blast Lung Injury, Biomolecules 2023, 13, 351. https://doi.org/10.3390/biom13020351.

[31] Jeon D, Kim K, Han S. Modified Equation of Shock Wave Parameters. Computation. 2017; 5(3): 1-14. https://www.mdpi.com/2079-3197/5/3/41 Consultado: Julio 5, 2021, 10:00 am]

[32] Dadashzadeh H, Khan F, Hawboldt K, Amyotte P. An integrated approach for fire and explosion consequence modelling. Fire Safety Journal. 2013; 61: 324-337

[33] Cozzani V, Tugnoli A, Salzano E. Prevention of domino effect: From active and passive strategies to inherently safer design. J Hazard Mater 2007; A139: 209-219.

[34] Khan F, Abbasi SA, Models for Domino Effect Analysis in Chemical Process Industries, Process. Saf. Prog 1998; 17(2): 107-123

[35] Yin-chua, Lu. “Application of Matlab simulation in boiler explosion quantitative safety assessment.” Manufacturing Automation (2012): n. pag.

[36] Birk AM, Davison C, Cunningham M. Blast overpressures from medium scale BLEVE tests. J Loss Prev Process Ind 2007; 20: 194-206.

[37] Van de Berg AC, Lannoy A. 1993. Methods for Vapor Cloud Explosion Blast Modelling. Journal of Hazardous Materials. 1993; 34, 151-171.

[38] Bubbico R, Mazzarotta B. Analysis and comparison of calculation methods for physical explosions of compressed gases. AIDIC Conference Series. 2013; 11: 81-90 DOI: 10.3303/ACOS1311009

[39] Sochet I. Blast effects of external explosions. In: Eighth International Symposium on Hazards, Prevention and Mitigation of Industrial Explosions. Yokohama, Japón: Sep. 2010. https://hal.archives-ouvertes.fr/hal-00629253/document [Consultado: Julio 5, 2022, 3:28 pm]

[40] T. E. Purcell and S. F. Whirl. Protection Against Caustic Embrittlement by Coordinated Phosphate‐pH Control 1943 Trans. Electrochem. Soc. 83 343.

[41] Zareei H, Khosravi-Nikou M, Shariati A. (2016). A Consequence Analysis of the Explosion of Spherical Tanks Containing Liquefied Petreoleum Gas (LPG). Iranian Journal of Oil & Gas Science and Technology. 2016; 5(3): 32-44

[42] Affandi M, Mamat N, Kanafiah S, Khalid N. (2013). Simplified Equations for Saturated Steam Properties for Simulation Purpose. Procedia Engineering 53; 722 – 726.

[43] Cozzani V, Tugnoli A, Salzano E. Prevention of domino effect: From active and passive strategies to inherently safer design. Journal of Hazardous Materials. 2007; A139: 209-219.

[44] Cozzani V, Salzano B. Threshold values for domino effects caused by blast wave interaction with process equipment. Journal of Loss Prevention in the Process Industries. 2004; 17, 437-447.

[45] Cozzani V, Gubinelli G, Salzano B. (2006). Escalation thresholds in the assessment of domino accidental events. Journal of Hazardous Materials. 2006; A129: 1-21.

[46] Finney, D, L. Probit Analysis. Cambridge University Press. Londres, 1971.

[47] López.Molina A, Vázquez-Román R, Sam Mannan M, Félix-Flores MG. An approach for domino effect reduction based on optimal layouts. Journal of Loss Prevention in the Process Industries. 2013; 26: 887-894.

[48] Sajja, V.S., Statz, J.K., Walker, L.P.B. et al. Pulmonary injury risk curves and behavioral changes from blast overpressure exposures of varying frequency and intensity in rats. Sci Rep 10, 16644 (2020). https://doi.org/10.1038/s41598-020-73643-7

[49] Morales-Vargas R. Using MATLAB for calculation of boiler explosion consequences: An application to plant layout using Probit models, J. Res. Technol. Eng. 3 (3), 2022, 21-31

[50] A. Davenport, JACOBS Solutions, comunicación personal, Abril 2023.

Declaración sobre uso de Inteligencia Artificial (IA)

El autor aquí firmante declara que no se utilizó ninguna herramienta de IA para la conceptualización, traducción o redacción de este artículo.

---

1. 1 Departamento de Salud Ambiental- Escuela de Tecnologías en Salud. Facultad de Medicina. Universidad de Costa Rica. Costa Rica.
   ricardo.morales@ucr.ac.cr
   https://orcid.org/0000-0002-8417-992X