Effect of instance selection algorithms on prediction error of numerical variables
Efecto de los algoritmos de selección de instancias sobre el error de predicción de variables numéricas
Martín Solís1, Erick Muñoz-Alvarado2
Fecha de recepción: 7 de diciembre, 2023
Fecha de aprobación: 14 de marzo, 2024
Solís, M; Muñoz-Alvarado, E. Effect of instance selection algorithms on prediction error of numerical variables . Tecnología en Marcha. Vol. 38, No 1. Enero-Marzo, 2025. Pág. 157-171. https://doi.org/10.18845/tm.v38i1.6937
https://doi.org/10.18845/tm.v38i1.6937
Keywords
Instance selection algorithms; regression task; machine learning; noise.
Abstract
The main objective of this study is to analyze the effect of instance selection (IS) algorithms on the prediction error in regression tasks with machine learning. Six algorithms were evaluated; four from literature and two are new variants of one of them. Different percentages and magnitudes of noise were added to the output variable of 52 datasets to evaluate the algorithms. The results show that not all IS algorithms are effective. RegENN and its variants improve the prediction error (RMSE) of the regression task in most datasets for high percentages and magnitudes of noise. However, when the magnitude and percentage of noise are lower, for example, 10%-10%, 50%-10%, or 10%-30%, there is no evidence of improvement in most datasets. Other results are presented to answer four new questions about the performance of the algorithms.
Palabras clave
Algoritmos de selección de instancias; tareas de regresión; aprendizaje automático; ruido.
Resumen
El objetivo principal de este estudio es analizar el efecto de los algoritmos de selección de instancias (IS) sobre el error de predicción en tareas de regresión con machine learning. Se evaluaron seis algoritmos; cuatro de la literatura y dos son nuevas variantes de uno de ellos. Se agregaron diferentes porcentajes y magnitudes de ruido a la variable de salida de 52 conjuntos de datos para evaluar los algoritmos. Los resultados muestran que no todos los algoritmos IS son efectivos. RegENN y sus variantes mejoran el error de predicción (RMSE) de la tarea de regresión en la mayoría de los conjuntos de datos para altos porcentajes y magnitudes de ruido. Sin embargo, cuando la magnitud y el porcentaje de ruido son menores, por ejemplo, 10 %-10 %, 50 %-10 % o 10 %-30 %, no hay evidencia de mejora en la mayoría de los conjuntos de datos. Se presentan otros resultados para responder a cuatro nuevas preguntas sobre el rendimiento de los algoritmos.
Introduction
Instance selection (IS) is useful to choose a subset of data without noise or with more relevant instances [1]. Two of the main purposes of instance selection are reducing a dataset and improving performance in data mining or machine learning tasks by cleaning redundant instances, outliers, and noise instances [2]. Our work analyzes how the application of instance selection algorithms affects performance in regression tasks when there is noise in the training dataset.
In supervised tasks, an instance is noisy when it has suffered a corruption that alters the relationship between the informative features and the output [1]. When the noise is present in the input attributes, it is known as attribute noise, and when it is present in the output variable is known as class noise [3]. The last one is more harmful in supervised classification tasks [5], and maybe, for this reason, several filters have been developed for its detection. These filters have been effective for the classification task. For example, Garcia et al. [1] show the effect of three noise filters to detect and delete instances in datasets with uniform class noise and pair-wise class noise at ranges from 5 to 20%. SVM, Ripper, and C4.5’s mean accuracy was better when the filter was applied to delete noise instances from datasets. Also, in [5], it is shown how some filter algorithms contribute to improve the classification performance in problems with different percentages of class noise.
As well as these studies, many others have emerged that analyze the performance of noise detection algorithms in classification problems, for example [6, 10,11,12, 18, 19]. However, for regression problems, the development and performance evaluation of filter algorithms has not been widely studied. Some of the most relevant studies come from [7, 8, 9].On the hand, the findings for noise detection in classification supervision tasks cannot be generalized to regression tasks. In classification, the instance selection algorithm looks for deviations at a class between a finite number of classes; however, in regression, the output could be continuous or with a broad range of values [7]. Therefore, in regression, the IS algorithm should set a variable threshold of the difference between the predicted and the actual value of the vector output to define an instance as noisy [9].
The main objective of this study is to analyze the effect of IS algorithms on the prediction error in regression tasks. Arnaiz-González et al. [7, 17] analyzed the effect of a few IS algorithms on performance prediction in the regression task, including different noise percentages in 29 datasets. However, in our study, we consider the percentage of noisy instances and the magnitude of noise, while including more datasets, four algorithms taken from literature, and two new variants of one of them. Precisely, we aim to answer the following new questions about IS algorithms for regression:
1.Are the IS algorithms effective in improving the prediction error of the regression task at different percentages of noisy instances and magnitudes of noise in the output variable?
2.Are the IS algorithms effective in improving the prediction error of the regression task when there is no noise in the output variable?
3.Which of the IS algorithms is the best at reducing the prediction errors in the regression task, considering different percentages of noisy instances and magnitudes of noise?
Related work
A few studies have proposed algorithms, for instance selection in regression tasks. These algorithms can be used for noise detection in the output variable [8], but also in data reduction, deleting redundant instances [8] or outlier detection [9].
According to [4], there are two kinds of Instance selection algorithms for regression: evolutionary-based and nearest neighbor-based. In the first group, we found the genetic algorithm developed by [16] to detect outliers in regression problems and the multi-objective evolutionary learning of fuzzy rule-based systems proposed by [15]. In the second group, there are more options: Kordos and Blahnik [9] adapted the Edited Nearest Neighbor rule (ENN) and Condensed Nearest Neighbor rule (CNN) for instance selection in classification problems to regression problems. They were called RegENN and RegCNN, respectively. Arnaiz-González et al. [4, 7, 17] proposed several variations using KNN, for example, 1) discretizes the output variable to apply ENN and CNN, 2) Create a bagging ensemble with RegENN and RegCNN, 3) ensemble of discretization-based ENN and ensemble of discretization-based CNN, 4) adaptations and variants of DROP instance selection methods used in classification. Song et al. [8] developed a KNN algorithm named DISKR that deletes noise or redundant instances to reduce the training dataset.
In [22] the authors evaluate the performance of an evolutionary algorithm, for instance, selection in regression. They evaluated different parameters of the algorithm and its influence on the results. Also, [23] used a genetic algorithm, for instance, selection in regression. The authors demonstrate that their proposal improves the predictive model performance compared to instance selection performed on the complete training dataset. In order to attend to the problem of instance selection for multi-target regression tasks [24], proposed an ensemble algorithm. They showed the effectiveness of their proposal using 18 datasets. Finally, [25] developed an interactive nonparametric evidential regression algorithm with instance selection.
From the previous algorithms, we evaluated RegENN because is considered a noise filter [17] and shows the best RMSE when applied to datasets with 10% of noise [7]; DROP2-RE was selected because shows good performance detecting 10%, 20% and 30% of noisy instances in the datasets; DiscENN because when applied with 20%, 30%, and 40% of noise, the RMSE was the best; DISKR, since it has not been tested in problems with noise as far as we know, and shows good results reducing the dataset and keeping good performance in regression tasks [4, 8]. We propose two new options derived from RegENN, named RegENN2 and RegENN3. In the next section, we will describe these algorithms.
Algorithms 3
RegENN was proposed by [9] as an adaptation of Wilson ENN (used for classification instance selection). For each instance, 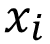 : a) A model (kNN in our case) for regression is trained without the instance; b) Get k-nearest neighbors of the instance
: a) A model (kNN in our case) for regression is trained without the instance; b) Get k-nearest neighbors of the instance 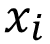 based on T; c) Compute the threshold θ that depends on the standard deviation of the k-nearest neighbors real values and a parameter α; d) Exclude an instance from T if the prediction error of is bigger than the threshold θ. The purpose of this model is to exclude an instance that has a prediction error α times greater than the variability of the numerical target in similar instances. The algorithm gets more rigorous at excluding instances when α decreases.
based on T; c) Compute the threshold θ that depends on the standard deviation of the k-nearest neighbors real values and a parameter α; d) Exclude an instance from T if the prediction error of is bigger than the threshold θ. The purpose of this model is to exclude an instance that has a prediction error α times greater than the variability of the numerical target in similar instances. The algorithm gets more rigorous at excluding instances when α decreases.
|
Algorithm1: Edited Nearest Neighbor for regression (RegENN) |
|
Data : Training set T = { (
Result : Instance set S ⊆ T |
|
1 for i = 1 . . . n do |
|
2 |
|
3 R = kNN (T\ |
|
4 ѳ= α.std(y( |
|
5 If | |
|
6 T = T\ |
|
end |
|
end |
|
7 S=T |
|
Return S |
We proposed two variations to RegENN. The first one was named RegENN2 and had two main differences. One is that the instances considered noisy were removed simultaneously instead of sequentially. We did this change to avoid the influence of the dataset order in the instance selection process. The second and most important, is that we changed the formula of the threshold ѳ. In RegENN2 ѳ is the product of the parameter α and the mean absolute error of the k-nearest neighbors. The idea of this change is to exclude an instance that has an absolute error prediction greater α times than the mean absolute error of its more similar instances. The algorithm is more rigorous when α decreases.
|
Algorithm2: RegENN2 |
|
Data : Training set T = { (
Result : Instance set S ⊆ T |
|
1 |
|
2 for i = 1 . . . n do |
|
3 |
|
4 |
|
5 ѳ= α .(MAE( |
|
6 If | |
|
7 |
|
end |
|
end |
|
8 S ={ T: |
|
Return S |
The second was named RegENN3. It assigns a weight to the features when the Euclidean distance is computed in the kNN prediction. The weights are taken from Random Forest Feature importance. This change pretends to reduce the importance of features that are less related to the target. Furthermore, a weight is assigned to the neighbor instances when the mean absolute error is computed. Closer instances of a specific instance have more weight. To that end, we divide the inverse distance of each instance neighbor by the sum inverse distances from all neighbors.
|
Algorithm3: RegENN3 |
|
Data : Training set T = { ( Result : Instance set S ⊆ T |
|
1 |
|
2 Imp= RandomForest(T\ |
|
3 for i = 1 . . . n do |
|
4 |
|
5 |
|
6 foreach k (instance neighbor) in 7 |
|
end |
|
8 ѳ= α .(MAE_weight\ |
|
9 If | |
|
10 |
|
end |
|
end |
|
11 S ={ T: |
|
Return S |
DiscENN was also proposed by [7] and showed better performance than RegENN to improve the regression prediction model when there is more than 10% noise [7]. A similar version was used in this paper, but we established the number of discretization categories k as a parameter instead of using leave-one-out entropy to be estimated. In this algorithm, the target value is discretized with equal-width binning. After that ENN instance selection algorithm for classification is applied, and the categorical target is restored to get the subset S finally.
|
Algorithm4: Discretization for Edited Nearest Neighbor |
|
Data : Training set T = { (
Result : Instance set S ⊆ T |
|
1 |
|
2 Apply ENN on (x, |
|
3 Restore the numerical value of |
|
Return S |
Song et al. [8] developed a kNN algorithm named DISKR that deletes noise or redundant instances to speed up executing prediction and improve the learners’ performance in regression tasks. They compare the performance of DISKR with other algorithms that had a similar purpose, using 19 datasets. The results showed that the application of DISKR did not display better or worse R² in regression tasks, when compared to other instance selection algorithms. However, the DISKR lowers the storage ratio and therefore speeds up the execution time. This algorithm has three parts: First, excluding outliers instances with a higher absolute prediction error than the threshold (1 - ѳ) multiplied by the target. Second, ordering the included instances by the absolute difference between target and prediction. Third, the objective is to remove the instances that generate a higher residual sum of squares when excluded from the dataset.
|
Algorithm 5: Decremental instance selection for kNN regression (DISKR) |
|
Data : Training set T = { (
Result : Instance set S ⊆ T |
|
1 |
|
2 for i = 1 . . . n do |
|
3 |
|
4 if | |
|
5 |
|
end |
|
end |
|
6 S ={ T: |
|
7 |
|
8 foreach instance i in |
|
9 compute |
|
10 if |
|
11 S= S-{i} |
|
12 foreach j ϵ |
|
13 Find another instance h to replace j in |
|
14= |
|
end |
|
end |
|
end |
|
Return S |
DROP2-RE is an adaptation of Drop methods [20] used in classification problems. According to [17], the idea is to remove an instance if it does not increase its associates prediction error. The instances that have p as one of its k nearest neighbors are called associates of p. DROP2- RE was between the two best algorithms considering the accuracy in the prediction task, when there was a noise percentage of 10%, 20%, and 30%, according to experiments in [17].
|
Algorithm 6: DROP2-RE: adaptation to regression of DROP2 by using error accumulation. |
|
Data : Training set T = { (
|
|
Result : Instance set S ⊆ T |
|
Let S =T |
|
1 foreach instance x in S do |
|
2 find x. 3 Add x to each of its list of the associates of the neighbours |
|
4 foreach instance x in S do |
|
5 Let ewith=0 |
|
6 Let ewithout=0 |
|
7 Foreach associate a of x do |
|
8 Add |
|
9 Add |
|
10 if ewithout <= ewith then |
|
11 Remove x from S |
|
12 Foreach associate a of x do |
|
13 Remove x from a list of nearest neighbours |
|
14 Find a new nearest neighbour for a |
|
15 Add a to its new neighbour’s list of associates |
|
Return S |
Methods
Datasets
We used 52 datasets from the Keel repository [13] and UCI machine-learning repository [14]. The datasets used are in Repository. The number of instances of the datasets are between 209 and 5723, with an average of 2429. The number of input features is between 3 and 82. The average correlation between the input features is between 0.03 and 0.86.
Instance selection algorithms and parameters
The algorithms explained in the previous sections could be used with different methods. For example, in RegENN, the model (T\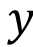 ,
,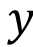 ) could be calculated with KNN or another option. However, we decided to use KNN because of its simplicity. KNN was applied with k=9 following the recommendation of the authors [7].
) could be calculated with KNN or another option. However, we decided to use KNN because of its simplicity. KNN was applied with k=9 following the recommendation of the authors [7].
On the other hand, five of the six algorithms have one parameter that should be defined. We evaluated each algorithm with four different parameter values considering what was used in other studies [7, 8, 17]. The parameters used in the experiments are shown below:
•RegENN, RegENN2, RegENN3 were applied with alpha = 0.5, 1, 3, 5.
•DiscENN with bins = 2,3,4,5.
•DISKR with alpha = 0.05, 0.1, 0.2, 0.3
•DROPRE2 = It does not have a parameter
Experimental setup
We followed some principles of the method used by [7, 19] to evaluate the six algorithms’ effect on the prediction error of the regression task. Figure 1 describes the experimental process applied for each dataset.
4.First, we split the dataset in training and test (we used 5-fold cross-validation).
5.A magnitude of noise was added to the output variable of some instances of the training set. For the noise incorporation, a percentage of instances were selected randomly. We multiplied the value of the output variable by the magnitude of noise, and the result was added or subtracted to the output variable.
6.Next, we applied the IS algorithm to the training set in order to detect the noisy instances. Each instance classified as noisy was deleted from the training set.
7.Then, we trained a Random Forest Regressor with the training set to predict the output variable. The Random Forest was trained with 100 trees, and a maximum depth of 9. We chose the Random Forest because it is highly used in regression tasks with good performance [26, 27], and has been successfully insensitive to over-fitting [28].
8.Finally, with the model trained, we predicted the output variable of the test dataset and computed the Root Mean Square Error.
Figure 1.Experimental process, based on [7]
The process depicted in figure 1 was applied 13 times for each dataset. The first time is applied using the original dataset without noise incorporations into the output variable in the step 2. In the following twelve times, we used different magnitudes and percentages of noise. The magnitudes of the noise used were: 10%, 50%, 100% and 200% while the percentages of noisy samples were: 10%, 30% and 50%. Thus, in each of the twelve times, we applied a combination of the percentage of noisy instances and the noise magnitude. In experimental terms, it is a factorial design 4*3 for repeated measures. A random seed was fixed to guarantee the comparability. The algorithms and the experimental setup were programmed in Python, and the data analysis in R.
Results
Influence of IS algorithms on the prediction error of the regression task
In order to show pieces of evidence to questions one and two, we calculated the relative change in the RMSE when using an IS algorithm versus not using it for each percentage and magnitude of noise. Figure 2 shows the confidence interval of the proportions of cases (datasets) where the relative change decreases when the IS algorithm was used at different percentages (percentage) and magnitudes of noise. Figure 3 complements the information of figure 2 with a box plot of the relative change.
According to the punctual percentage estimation and the box plots, the algorithms RegENN, RegENN2 and RegENN3 tend to be more effective as the noise magnitude increases independent of the noise percentage. Based on the interval confidence, we cannot conclude that these algorithms are effective in most cases when there is no noise or when the magnitude and percentage noise are: 10%-10%, 10%-30%. DiscENN is effective in most cases when noise magnitude is 100% and 200% with a noise percentage of 10%, and DROPRE2 is effective when the magnitude is 200% with noise percentages of 10% and 30%, although the percentage decrease in RMSE tends to be modest in these cases for both algorithms (Figure 2).
Figure 2. Confidence intervals of the proportion of datasets where the RMSE decreases when the IS algorithm is applied vs not applied, according to magnitude and percentage of noise.
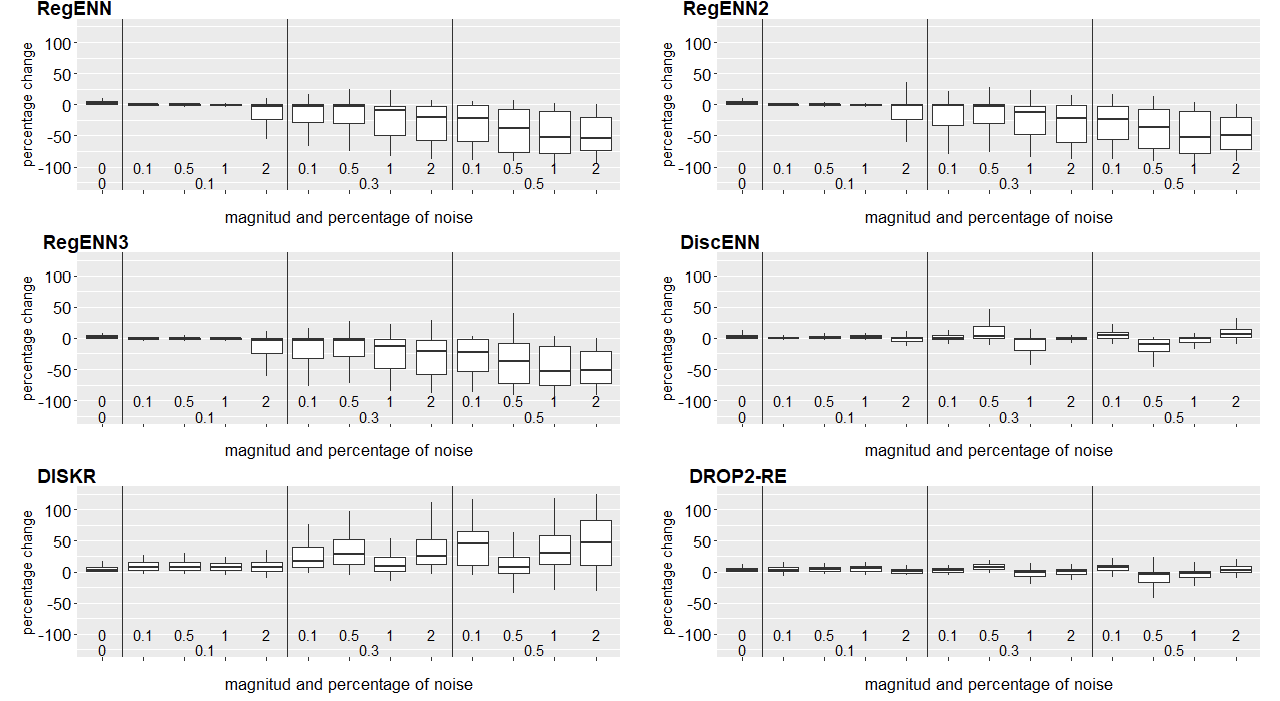
Figure 3. Box plot of the relative change in the RMSE when the IS algorithm is applied vs. not applied, for each percentage and magnitude of the noise
Best algorithm
Table 1 presents evidence for question 3. This table has the average rank of each algorithm for each combination of noise percentage and noise magnitude. For example, the first number in RegENN shows that in the 52 datasets, this algorithm got an average position of 2.1 between the six algorithms when the dataset has 0% of noise. The Anova test indicates that at least one mean differs from the others in each scenario (a combination of percentage and magnitude of noise), p<0.05. Because of the previous result, we applied paired t-test with Bonferroni correction to analyze which means have a significant statistical difference with the best mean. This test showed that RegENN, RegENN2, RegENN3 were the best algorithms in 11 scenarios, while in the scenarios where the percentage of noise was 0.1, and the magnitudes were 1 and 2, the best were RegENN2, RegENN3.
Although the algorithms DiscENN, DISKR, and DROP2-RE had the worst performance on average, in some datasets, these got the best performance (table 2). For example, with a percentage and magnitude of 10%, there were 17% (9 datasets) of datasets where DiscENN gave the best reduction in RMSE.
Table 1. Average rank over the relative change in RMSE when IS is used (vs. not used), for each algorithm.
|
Percentage |
Magnitude |
Algorithms |
|||||
|---|---|---|---|---|---|---|---|
|
RegENN |
RegENN2 |
RegENN3 |
DiscENN |
DISKR |
DROP2-RE |
||
|
0 |
0 |
2.1a |
2.7a |
2.6a |
3.5 |
5.3 |
4.8 |
|
0.1 |
0.3 |
2.5a |
2.4a |
2.4a |
3.5 |
5.4 |
4.8 |
|
0.1 |
0.5 |
2.3a |
2.5a |
2.1a |
3.9 |
5.6 |
4.6 |
|
0.1 |
1 |
2.6 |
2.2a |
2a |
3.8 |
5.7 |
4.7 |
|
0.1 |
2 |
2.6 |
1.8a |
2.1a |
4.2 |
5.6 |
4.6 |
|
0.3 |
0.1 |
2.2a |
2.5a |
2.2a |
3.8 |
5.5 |
4.8 |
|
0.3 |
0.5 |
2.1a |
2.4a |
2.2a |
4.1 |
5.7 |
4.5 |
|
0.3 |
1 |
2.3a |
2.3a |
2.1a |
4.1 |
5.7 |
4.6 |
|
0.3 |
2 |
2.2a |
2.3a |
1.9a |
4.3 |
5.7 |
4.6 |
|
0.5 |
0.1 |
2.2a |
2.4a |
2.2a |
3.9 |
5.3 |
5.0 |
|
0.5 |
0.5 |
1.9a |
2.4a |
2.4a |
4.0 |
5.8 |
4.5 |
|
0.1 |
1 |
2.3a |
2.3a |
2.2a |
3.9 |
5.8 |
4.6 |
|
0.5 |
2 |
1.9a |
2.1a |
2.2a |
4.5 |
5.8 |
4.5 |
a best algorithms according to paired t-test with Bonferroni correction
Table 2. Relative distribution of the datasets according to the algorithm that got the best relative change in RMSE by each percentage and magnitude of noise.
|
Percentage |
Magnitude |
Algorithms |
||||||
|---|---|---|---|---|---|---|---|---|
|
RegENN |
RegENN2 |
RegENN3 |
DiscENN |
DISKR |
DROP2-RE |
Total |
||
|
0 |
0 |
40% |
15% |
29% |
8% |
4% |
4% |
100% |
|
0.1 |
0.1 |
23% |
31% |
27% |
17% |
2% |
0% |
100% |
|
0.5 |
29% |
13% |
40% |
13% |
4% |
0% |
100% |
|
|
1 |
12% |
31% |
40% |
12% |
4% |
2% |
100% |
|
|
2 |
10% |
54% |
23% |
8% |
4% |
2% |
100% |
|
|
0.3 |
0.1 |
33% |
21% |
33% |
8% |
4% |
2% |
100% |
|
0.5 |
37% |
23% |
29% |
8% |
4% |
0% |
100% |
|
|
1 |
25% |
23% |
42% |
6% |
4% |
0% |
100% |
|
|
2 |
31% |
19% |
44% |
2% |
2% |
2% |
100% |
|
|
0.5 |
0.1 |
27% |
29% |
29% |
8% |
6% |
2% |
100% |
|
0.5 |
42% |
21% |
21% |
13% |
0% |
2% |
100% |
|
|
1 |
29% |
29% |
27% |
12% |
0% |
4% |
100% |
|
|
2 |
46% |
27% |
21% |
4% |
2% |
0% |
100% |
|
Conclusions
This study provides new evidence about the influence of the IS algorithms on the prediction error in learning regression tasks. The research questions posed in the introduction with our answers based on the results are shown below.
1. Are the IS algorithms effective in improving the prediction error of the regression task at different percentages of noisy instances and magnitudes of noise in the output variable?
Not all IS algorithms are effective. The RegENN and its variants tend to improve the prediction error of the regression task in most datasets for high percentages and magnitudes of noise. The RMSE reduction fluctuates between 0% and 100%. Nonetheless, when the magnitude and percentage of noise are lower, for example, 10%-10%, 50%-10%, or 10%-30%, there is no evidence of improvement in most datasets, and when it occurs, it is close to zero. Concerning the other algorithms, these are not effective in over 50% of datasets for the majority percentages and magnitudes of noise.
2. Are the IS algorithms effective in improving the prediction error of the regression task when there is no noise in the output variable?
The IS algorithms are not effective in improving the prediction error of the regression task when there is no noise in the output variable. The RegENN and its variants tend to be effective around 50% of datasets, and with other algorithms, this percentage is lower. Besides, when there is an improvement in performance prediction, the percentage reduction in RMSE is close to 0%.
3. Which of the IS algorithms is the best at reducing the prediction errors in the regression task, considering different percentages of noisy instances and magnitudes of noise?
RegENN, RegENN2, RegENN3 were the best algorithms in 11 scenarios (combination of percentage and magnitude of noise), while in the scenarios where the percentage of noise was 0.1, and the magnitudes were 1 and 2, the best were our proposals RegENN2, RegENN3. Although the algorithms DiscENN, DISKR, and DROP2-RE had the worst on average, in some datasets, these got the best performance. For this reason, it is convenient to develop a model that can tell us which algorithm is the best option, according to the characteristics of the dataset.
Future Research lines
Future studies should analyze what dataset features influence the effectiveness of IS algorithms to reduce the error in the regression task and develop a model that can tell us which algorithm is the best option according to the characteristics of the dataset.
Our findings suggest that the IS algorithm is not effective when the noise percentage and magnitude is lower, for example, 10% of noise with a magnitude of 10% and 50% of the real value. Therefore, new algorithms should be proposed to reduce the error in the regression task for low values of noise percentage and noise magnitude.
References
[1] S. García, J. Luengo, F. Herrera, Data preprocessing in data mining, Springer, 2015. doi:10.1007/978-3-319-10247-4
[2] H.Liu, H.Motoda, On issues of instance selection, Data Min. Knowl. Disc. 6(2) (2002) 115–130
[3] S. García, J. Luengo, F. Herrera, Tutorial on practical tips of the most influential data preprocessing algorithms in data mining, Knowledge-Based Systems, 98 (2016) 1-29 https://doi.org/10.1016/j.knosys.2015.12.006
[4] A. Arnaiz-González, M. Blachnik, M. Kordos, C. García-Osorio, Fusion of instance selection methods in regression tasks, Information Fusion 30 (2016) 69–79 https://doi.org/10.1016/j.inffus.2015.12.002
[5] X. Zhu , X. Wu, Class noise vs. attribute noise: a quantitative study, Artif. Intell. Rev. 22 (2004) 177–210 https://doi.org/10.1007/s10462-004-0751-8
[6] J.Sáez, M. Galar, M. Luengo, F. Herrera, INFFC: an iterative class noise filter based on the fusion of classifiers with noise sensitivity control. Information Fusion 27 (2016) 19-32 https://doi.org/10.1016/j.inffus.2015.04.002
[7] A. Arnaiz-González, J. F. Díez-Pastor, J.J .Rodríguez, C. I. García-Osorio, Instance selection for regression by discretization, Expert Systems with Applications 54 (2016) 340-350. https://doi.org/10.1016/j.eswa.2015.12.046
[8] Y.Song, J. Liang, J.Lu, X.Zhao, X, An efficient instance selection algorithm for k nearest neighbor regression, Neurocomputing, 251 (2017) 26-34 https://doi.org/10.1016/j.neucom.2017.04.018
[9] M.Kordos, M. Blachnik, Instance selection with neural networks for regression problems, in: A.E.P. Villa, W.Duch, P.Érdi, F.Masulli, G.Palm(Eds.),Artificial Neural Networks and Machine Learning ICANN 2012, volume 7553 of Lecture Notes in Computer Science, Springer Berlin Heidelberg, 2012, pp. 263–270 https://doi.org/10.1007/978-3-642-33266-1_33
[10] L. Daza, E. Acuna, An algorithm for detecting noise on supervised classification, in: Proceedings of the 1st World Conference on Engineering and Computer Science (WCECS), October 2007, San Francisco, USA, pp. 701–706.
[11] F. Benoît, M.Verleysen, Classification in the presence of label noise: a survey.” IEEE transactions on neural networks and learning systems 25(5) (2013) 845-869 https://doi.org/10.1109/tnnls.2013.2292894
[12] B.Zerhari, A. Lahcen, S. Mouline. Detection and elimination of class noise in large datasets using partitioning filter technique. in 2016 4th IEEE International Colloquium on Information Science and Technology (CiSt), 2016 https://doi.org/10.1109/cist.2016.7805041
[13] J. Alcalá-Fdez, A. Fernández, J. Luengo, J. Derrac, J, S. García, Keel data- mining software tool: Data set repository, integration of algorithms and experimental analysis framework, Multiple-Valued Logic and Soft Computing, 17 (2011) 255–287.
[14] D, Dua, C. Graff, UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science, 2019
[15] M. Antonelli, P. Ducange, F. Marcelloni, Genetic training instance selection in multi objective evolutionary fuzzy systems: A coevolutionary approach, IEEE Transactions on Fuzzy Systems 20 (2) (2012) 276–290 https://doi.org/10.1109/tfuzz.2011.2173582
[16] J. Tolvi, Genetic algorithms for outlier detection and variable selection in linear regression models, Soft Computing 8 (8) (2004) 527–533 https://doi.org/10.1007/s00500-003-0310-2
[17] A. Arnaiz-González, J.F.Díez-Pastor, J.J. Rodríguez, C.García-Osorio, Instance selection for regression: Adapting DROP, Neurocomputing, 201 (2016) 66-81 https://doi.org/10.1016/j.neucom.2016.04.003
[18] X. Zhu Wu, X, Class noise vs attribute noise: a quantitative study, Artif.Intell.Rev, 22 (3) (2004) 177–210 https://doi.org/10.1007/s10462-004-0751-8
[19] A. Guillen, L. J. Herrera, G. Rubio, H. Pomares, A. Lendasse, I. Rojas, New method for instance or prototype selection using mutual information in time series prediction, Neurocomputing 73 (10) (2010) 2030–2038 https://doi.org/10.1016/j.neucom.2009.11.031
[20] D.R. Wilson, T.R Martinez, Instance Pruning Techniques, ICML’97, 1997, pp. 403-411.
[21] T. Snijders, R. Bosker, Multilevel analysis: an introduction to basic and advanced multilevel modeling, Sage, 1999.
[22] M. Kordos, K. Łapa, Multi-Objective Evolutionary Instance Selection for Regression Tasks, Entropy, 20(10) (2018) 1-34 https://doi.org/10.3390/e20100746
[23] M. Kordos, M. Blachnik, R. Scherer, Fuzzy Clustering Decomposition of Genetic Algorithm-based Instance Selection for Regression Problems, Information Sciences, 587 (2021) 23-40 https://doi.org/10.1016/j.ins.2021.12.016
[24] C. Gong, P. Wang, Z. Su, An interactive nonparametric evidential regression algorithm with instance selection, Soft Computing, 24(5) (2020), 3125–3140 https://doi.org/10.1007/s00500-020-04667-4
[25] O. Reyes, H. M. Fardoun, S. Ventura, An ensemble-based method for the selection of instances in the multi-target regression problem, Integrated Computer-Aided Engineering, 25(4) (2018) 305–https://doi.org/10.3233/ica-180581
[26] M. Belgiu and L. Drăguţ, Random forest in remote sensing: A review of applications and future directions, ISPRS Journal of Photogrammetry and Remote Sensing, 114, (2016) 24–31 https://doi.org/10.1016/j.isprsjprs.2016.01.011
[27] M. Kayri, I. Kayri, and M. T. Gencoglu, The performance comparison of Multiple Linear Regression, Random Forest and Artificial Neural Network by using photovoltaic and atmospheric data, 2017 14th International Conference on Engineering of Modern Electric Systems (EMES), Jun. 2017. DOI: 10.1109/EMES.2017.7980368
[28] M. Čeh, M. Kilibarda, A. Lisec, and B. Bajat, Estimating the Performance of Random Forest versus Multiple Regression for Predicting Prices of the Apartments, ISPRS International Journal of Geo-Information, 7, (2018), 1-16 doi:10.3390/ijgi7050168
Declaración sobre uso de Inteligencia Artificial (IA)
Los autores aquí firmantes declaramos que no se utilizó ninguna herramienta de IA para la conceptualización, traducción o redacción de este artículo.
1 Instituto Tecnológico de Costa Rica. Costa Rica
 marsolis@itcr.ac.cr
marsolis@itcr.ac.cr https://orcid.org/0000-0003-4750-1198
https://orcid.org/0000-0003-4750-11982 Instituto Tecnológico de Costa Rica. Costa Rica
 erickamacr3@gmail.com
erickamacr3@gmail.com https://orcid.org/0000-0002-6244-3398
https://orcid.org/0000-0002-6244-33983 The IS algorithms used are at ……
 ,
,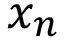 ,
,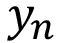
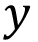 = prediction,
= prediction, 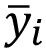 = Model (T\
= Model (T\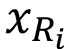 ))
))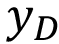 =Apply discretization of
=Apply discretization of 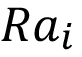 ,
, 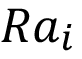
 ) , . . . (
) , . . . (