Caracterización climática de la lluvia del Pacífico Norte de Costa Rica usando análogos construidos

Climatic characterization of rainfall in the North Pacific of Costa Rica using constructed analogues

Kendall Ugalde1, Eric J. Alfaro2, Hugo G. Hidalgo3, Tito Maldonado4

Fecha de recepción: 16 de agosto, 2023
Fecha de aprobación: 6 de diciembre, 2023

Ugalde, K; Alfaro, E. J; Hidalgo, H. G; Maldonado, T. Caracterización climática de la lluvia del Pacífico Norte de Costa Rica usando análogos construidos. Tecnología en Marcha. Vol. 37, No 4. Octubre-Diciembre, 2024. Pág. 3-20.

https://doi.org/10.18845/tm.v37i4.6842

Resumen

Se determina el inicio y término de la estación lluviosa (IELL y TELL respectivamente), además de la duración de la estación seca y lluviosa (DES y DELL respectivamente), con datos de precipitación en rejilla sobre Guanacaste para el periodo 1950-2020 conformado por el acople de dos conjuntos de datos, el primero es el conjunto Climate Hazards group Infrared Precipitation with Stations (CHIRPS) y el segundo siendo el reanálisis ERA5 al que se le aplicó un ajuste de escala para extender la cobertura temporal de los datos de CHIRPS. Se caracterizó su IELL, TELL, DELL y DES con estadísticos como la mediana, desviación estándar, rango inter cuartil y tendencias. Además, se relacionaron con fuentes de variabilidad climática como El Niño-Oscilación del Sur (ENOS), la temperatura superficial del océano Atlántico Tropical Norte (ATN) y la corriente en chorro de bajo nivel del Caribe (CLLJ, por sus siglas en inglés). Los datos representan adecuadamente la climatología del IELL, TELL, DELL, DES y las precipitaciones de la región, además de capturar la variabilidad asociada a la CLLJ y al acople de los océanos (ATN-ENOS), pero no la asociada al ATN y ENOS individualmente. Aunque no se pudo determinar si esto se debe a los datos de ERA5 o al método de reducción de escala usado, por lo que se recomienda verificar si ERA5 captura tal variabilidad oceánica al realizar el mismo análisis en un periodo de tiempo de 1980-2020 donde se tiene mayor disponibilidad de observaciones como estaciones meteorológicas o CHIRPS que ya ha sido validada.

Palabras clave

Duración de la Estación Seca y Lluviosa; Guanacaste; Inicio y Término de la Estación Lluviosa; Reducción de escala; Variabilidad Climática.

Abstract

The onset and demise of the rainy season (IELL and TELL, respectively in Spanish), also the duration of the dry and rainy seasons (DES and DELL, respectively in Spanish) are determined, with gridded precipitation data on Guanacaste for the period 1950-2020 constructed by coupling two data sets: 1) the dataset Climate Hazards group Infrared Precipitation with Stations (CHIRPS), and 2) the ERA5 reanalysis to which a downscaling method was applied to extend the data beyond the period covered by CHIRPS. Their IELL, TELL, DELL, and DES were characterized with statistics such as the median, standard deviation, interquartile range, and trends. In addition, were related to sources of climate variability such as El Niño Southern-Oscillation (ENSO), the sea surface temperature of the tropical north Atlantic (TNA) and the Caribbean Low-Level Jet (CLLJ). The dataset adequately represents the IELL, TELL, DELL, DES and the precipitations of the region, in addition to capturing the variability associated with the CLLJ and the coupling of the oceans (TNA-ENSO), but not that associated with the TNA and ENSO individually. Although it could not be determined if this is due to the ERA5 dataset or the downscaling method used, so it is recommended to verify if ERA5 captures such oceanic variability when performing the same analysis in a period of time from 1980-2020 where there is greater availability of observations such as meteorological gauge stations or CHIRPS that has already been validated.

Keywords

Climate Variability, Downscaling, Guanacaste, Onset and demise of the rainy season, Rainy and dry season duration.

Introducción

El establecimiento de las lluvias en América Central es un fenómeno que se ha estudiado por diversos autores [1]–[3], encontrando que el inicio de la estación lluviosa (IELL) tiende a ocurrir temprano (tarde) en los países al sur (norte) de la región, mientras el término de la estación lluviosa (TELL) exhibe un comportamiento contrario, asociando el fenómeno a la traslación latitudinal de la Zona de Convergencia Intertropical (ZCIT). Además, se ha determinado que fuentes de variabilidad climática como las temperaturas superficiales del mar en el Pacífico Tropical del Este y el Atlántico o la corriente en chorro de bajo nivel del Caribe (CLLJ, por sus siglas en inglés; [4], [5]) influyen en las lluvias de la región [1], [6], [7].

Son diversos los métodos usados para determinar las fechas del IELL y TELL, uno de los más comunes consiste en reducir las series temporales de precipitación en pentadas (promedios de 5 días) y buscar las que superen cierto umbral de precipitación de unos 25 mm para establecer el IELL, mientras que para el TELL se hace lo mismo recorriendo la serie en sentido contrario [3]. Sin embargo, en [8] se aplica un método más complejo basado en el estudio de [9] donde se buscan puntos de inflexión en las series de precipitaciones.

En [10] se usó el método de [8] para determinar el IELL y TELL, además de la duración de la estación seca y lluviosa (DES y DELL respectivamente) sobre Guanacaste usando datos de alta resolución espacial y temporal del conjunto denominado “Climate Hazards group Infrared Precipitation with Stations (CHIRPS)” de 1981 a 2020 [11]. Se encontró que los IELL ocurren antes en cantones centrales de Guanacaste cerca de la desembocadura del Tempisque, y más tarde hacia regiones costeras, al este y al norte de la provincia. Se determinó que los TELL son muy uniformes en la provincia, siendo más tardes al sur y más tempranos en la zona central y norte. Mientras que la DES y DELL, son simétricas entre sí y muy uniformes en la provincia mostrando las condiciones más secas al norte y las más húmedas al sur y este de la región. Además, las tendencias indican comportamientos hacia IELL más tempranos, TELL más tardíos, DES más cortas y DELL más largas.

Por otro lado, [10] también estudió la relación entre las fechas de la estación seca y lluviosa con diferentes fuentes de variabilidad climática como El Niño-Oscilación del Sur (ENOS), la Oscilación Multidecenal del Atlántico (OMA; [12], [13]) y la CLLJ. Principalmente determinó que un calentamiento relativo del Atlántico con respecto al Pacífico ecuatorial favorece que las lluvias inicien antes y acaben tarde, es decir la estación lluviosa se prolonga y la seca se acorta, para un enfriamiento relativo de los océanos se esperan condiciones contrarias. En el caso de una CLLJ intensa se favorecen condiciones secas, es decir las lluvias inician tarde y acaban antes, prolongando la estación seca y acortando la lluviosa, si la CLLJ es débil se esperan condiciones contrarias.

El conjunto de datos de CHIRPS permitió a [10] representar la estación seca y lluviosa sobre Guanacaste en un periodo de 40 años, sin embargo, contar con series de tiempo más extensas permitiría contemplar la variabilidad a mayor plazo. Existen conjuntos de datos temporalmente más extensos que CHIRPS, aunque cuentan con una resolución espacial mucho menor, lo que evitaría la captura de posibles fenómenos más locales en Guanacaste.

La resolución espacial se puede aumentar, como indican en [14] existen en general dos métodos de reducción de escala. El primero de ellos es el método de ajuste dinámico el cual usa un modelo regional de alta resolución con condiciones de frontera como función del tiempo derivadas del modelo de menor resolución, se puede considerar como un modelo regional inmerso en uno global, por lo que es muy importante identificar un modelo global que aporte la información más relevante al modelo regional (e.g. [15]). Mientras el segundo es el método de ajuste estadístico, el cual utiliza el mismo modelo de baja resolución y construye la información de alta resolución a partir de parámetros estadísticos o series de tiempo históricas, basados en relaciones empíricas entre predictores globales y predictantes regionales (e.g.[16]). Uno de estos métodos es el propuesto por [17] conocido como “Constructed Analogues (CA)” que consiste en construir un análogo de un patrón meteorológico diario de baja resolución espacial combinando patrones meteorológicos de varios días (predictores) de una biblioteca con patrones de alta resolución.

Esta investigación busca determinar las fechas del IELL, TELL, DES y DELL, utilizando la metodología de [9] modificada por [8] sobre datos de precipitación en rejilla que cubren toda la zona de Guanacaste, provenientes del acople de dos bases de datos, la primera el reanálisis ERA5 (1950-1980) [18] al que se le aplicó el método de reducción de escala CA y CHIRPS (1981-2020) [11] para conformar una base de datos a largo plazo llamada ERA5+CHIRPS (1950-2020). También se busca determinar la relación de estas fechas con fuentes de variabilidad climática que modulan las precipitaciones en América Central.

Materiales y métodos

Se utilizaron los datos de precipitación del reanálisis ERA5 [18] producidos por el Centro Europeo de Previsiones Meteorológicas a Plazo Medio (ECMWF por sus siglas en inglés). El reanálisis ERA5 se basa en el Sistema Integrado de Pronóstico operativo desde el 2016, que aprovecha los desarrollos posteriores al reanálisis ERA-Interim. ERA5 aumenta la resolución espacial a 31 km y su resolución temporal es de una hora, con datos disponibles desde 1950 hasta la actualidad. Comparaciones del ERA5 con otras bases de datos muestran una mejora para diversas variables, como lo es el aumento en la correlación de la media mensual de los datos de precipitación del Proyecto de Climatología de Precipitación Global (GPCP) [18].

El estudio se limitó sobre la región de Guanacaste, por lo que la resolución espacial de aproximadamente 31 km de ERA5 es baja. Sobre los datos de precipitación de ERA5 se aplicó el método de reducción de escala de CA según la metodología de [17], para obtener una base de datos con una mayor resolución espacial, de unos 5 km y que además de esta ventaja, permite extender el período de los datos a la cobertura temporal disponible de ERA5. La aplicación de la técnica de CA sobre los datos de ERA5 se hizo para generar una base de datos a largo plazo de 1950 a 2020, esta consistió en un acople de los datos de ERA5 con reducción de escala y los datos de CHIRPS usados por [10].

El conjunto de datos de precipitación (ERA5+CHIRPS) fue sometido a la metodología para determinar el IELL, TELL, DELL y DES de acuerdo con [8], que modifica el método expuesto por [9]. Esta fue usada recientemente por [10] en la región del Pacífico Norte de Costa Rica donde se explica detalladamente, en resumen el método aplica la ecuación 1 a las series de precipitación para calcular la desviación del acumulado de precipitación, luego la serie se suaviza usando una media móvil de 31 días y se buscan los puntos de inflexión que se relacionan con el IELL y TELL.

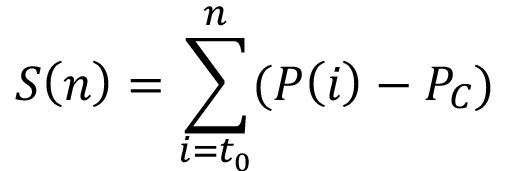Ecuación 1

Donde 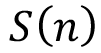es la desviación del acumulado de precipitación con respecto a la media anual en el día 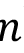, 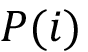es la precipitación diaria en el día 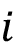, 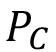es el promedio diario anual de precipitación y 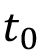es el día de inicio para los cálculos.

Se calcularon algunos parámetros estadísticos para caracterizar el comportamiento climatológico de los fenómenos en la región para el periodo de estudio. Estos fueron la media aritmética y mediana como medidas de localización y la desviación estándar y rango inter cuartil como medidas de dispersión. Además, se calcularon las tendencias mediante el método de mínimos cuadrados como una regresión lineal simple.

Diversas fuentes de variabilidad climática pueden influenciar en la época lluviosa y seca en América Central, en este caso se estudia el ENOS, la temperatura superficial del mar (TSM) del Atlántico Tropical Norte (ATN), la CLLJ y el dipolo entre las TSM del Pacífico y el Atlántico que ya han demostrado en influir en las lluvias de América Central (eg. [7], [20], [21]), aunque se debe tener en consideración que otros fenómenos con periodo intraestacional también afectan la climatología de las precipitaciones en la región como la oscilación Madden-Julian (OMJ) [22].

Para el ENOS, se usó la región del Niño 3.4 (N3.4) descrita por [23], abarcada entre las latitudes 5° N – 5° S y longitudes 170° O – 120° O, el índice asociado a estas anomalías de las TSM del N3.4 se encuentra disponible en el sitio web https://www.cpc.ncep.noaa.gov/data/indices/ersst5.nino.mth.81-10.ascii. Para el ATN se tomó el índice del sitio web https://psl.noaa.gov/data/correlation/tna.data, el índice abarca solo el Atlántico Tropical Norte (5.5° N – 23.5° N), para representar una región más tropical y cercana a América Central. Mientras que para calcular el índice asociado al dipolo entre las TSM del Atlántico y el Pacífico se normalizaron las series del ATN y N3.4 para luego realizar la resta ATN-N3.4.

Para el último índice asociado a la CLLJ se hizo lo mismo que en [7], promediando los datos de viento zonal a 925 hPa en la región 7.5° N – 12.5° N y 85° O – 75° O, esto según las características para la CLLJ descritas por [5], [19], [24].

Estos índices mensuales se promediaron en las mismas fechas usadas por [10], es decir como el IELL ocurre rondando mayo y el TELL rondando noviembre [1], se promediaron los índices de abril y mayo para relacionarlo al IELL, de octubre y noviembre para relacionarlo al TELL, de mayo a octubre para relacionarlo a la DELL y de noviembre (del año anterior) a abril (del año posterior) para relacionarlo a la DES, por la forma en la que se define esta última siempre contará con un año menos que el resto de índices. Como ejemplo, la figura 1 muestra el comportamiento del índice ATN-N3.4 en el periodo de 1950-2020.

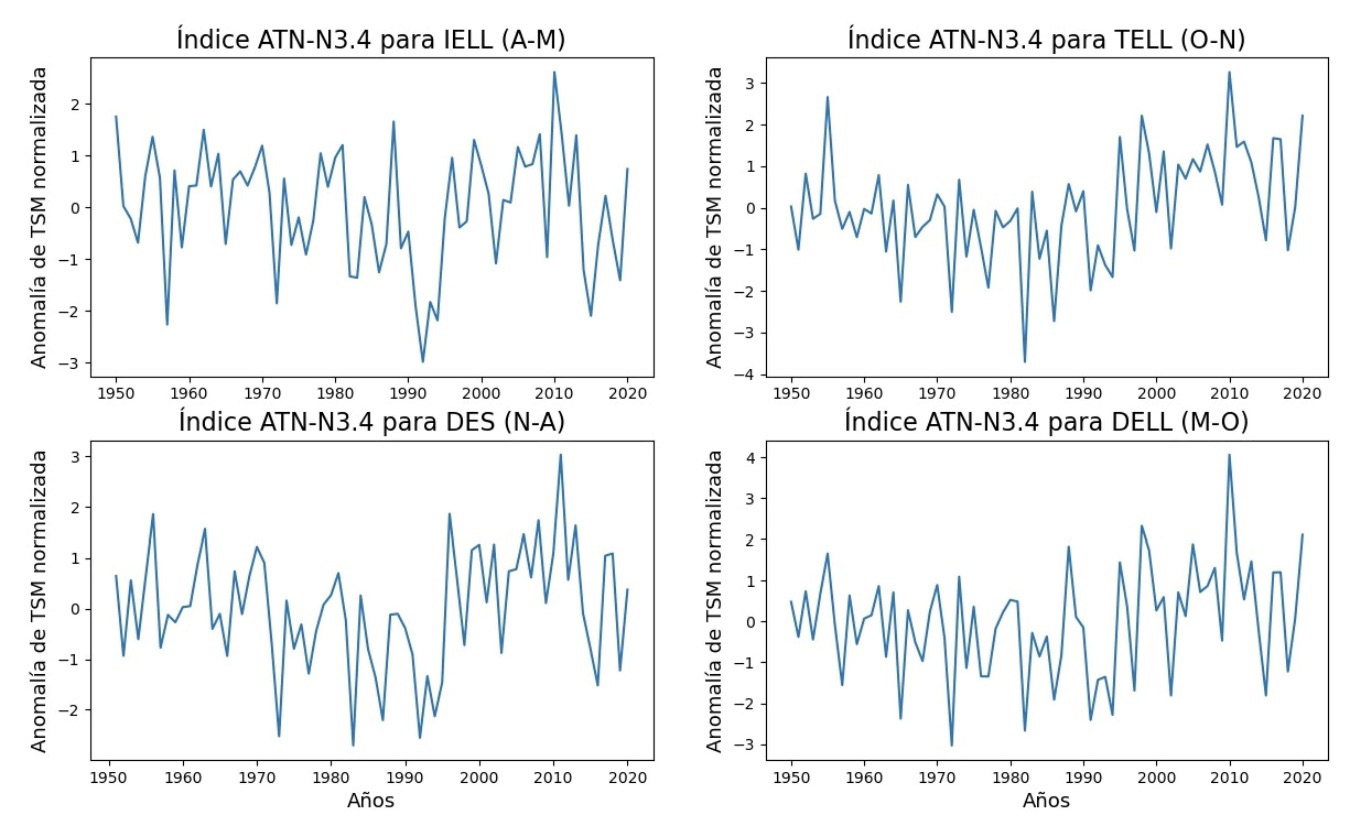
Figura 1. Índice ATN para 1950-2020 promediado en los periodos de abril-mayo para el IELL, de octubre-noviembre para el TELL, de noviembre (año anterior)-abril (año posterior) para la DES y de mayo-octubre para la DELL.

Para simplificar el proceso se usó el análisis de componentes principales (ACP) para reducir todo el conjunto de las series del IELL, TELL, DELL y DES obtenidos de ERA5+CHIRPS a unas pocas variables según indica [25]. Este consiste en generar un nuevo conjunto a partir de los autovalores y autovectores de la matriz de correlación de los datos originales. El método se adaptó a Python a partir de la rutina “EOFMOD.m” programada en Matlab por D.B. Enfield y con correcciones de F. J. Soley, la matriz de correlación se calculó con la paquetería Pandas de Python [26] y los autovalores y autovectores haciendo uso de las funciones de algebra lineal ofrecidas por la paquetería NumPy de Python [27]. Finalmente, con el scree-plot y la correlación de Pearson entre las primeras componentes principales (CP) con los datos originales se logró simplificar todo el conjunto ERA5+CHIRPS a una sola serie de tiempo.

Para comparar las CP asociadas al IELL, TELL, DELL y DES con los índices de variabilidad climática se calcularon entre ellos sus correlaciones de Pearson y se llevó a cabo una prueba t-student de dos colas para evaluar su significancia estadística. Además también se aplicó el análisis de tablas de contingencia detallado por [28], donde se usa la función de correlación cruzada entre una variable dependiente e independiente, siguiendo las recomendaciones de [28] usando solo tres categorías divididas por terciles indicando condiciones bajo lo normal (BN), normales (N) y arriba de lo normal (AN). Finalmente, se evaluó la significancia estadística de este método con una prueba χ2 y una prueba de Montecarlo.

Resultados

La figura 2 representa la mediana para las series del IELL, TELL, DES y DELL con resultados muy similares a los obtenidos usando solo CHIRPS (figura 3.1 de [10]). Se aprecia que la época lluviosa empieza más temprano en las zonas centrales, cerca del 5 de mayo y más tarde en las fronteras de la provincia de Guanacaste, cerca del 13 de mayo alcanzando valores más tardes al norte (La Cruz) de hasta el 18 de mayo. Por otro lado, las lluvias terminan más temprano en las zonas centrales, cerca del 3 de noviembre y más tarde al sur y este de la provincia, rondando el 14 de noviembre, a pesar de esto la distribución es bastante uniforme en casi todo Guanacaste.

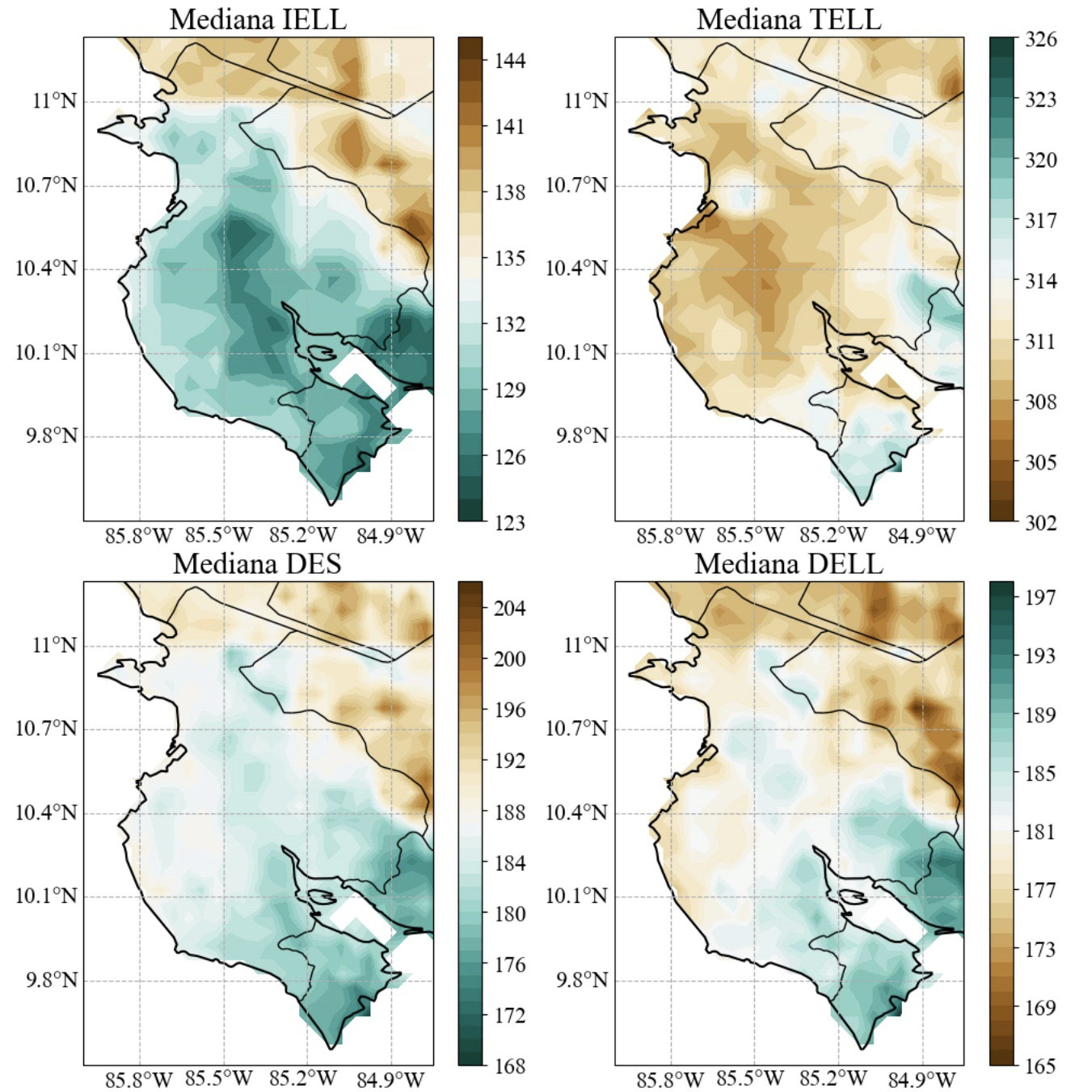
Figura 2. Mediana del día juliano del IELL y TELL, y mediana de la cantidad de días de la DES y DELL de la base de datos de ERA5+CHIRPS en la región de Guanacaste para el periodo 1950-2020.

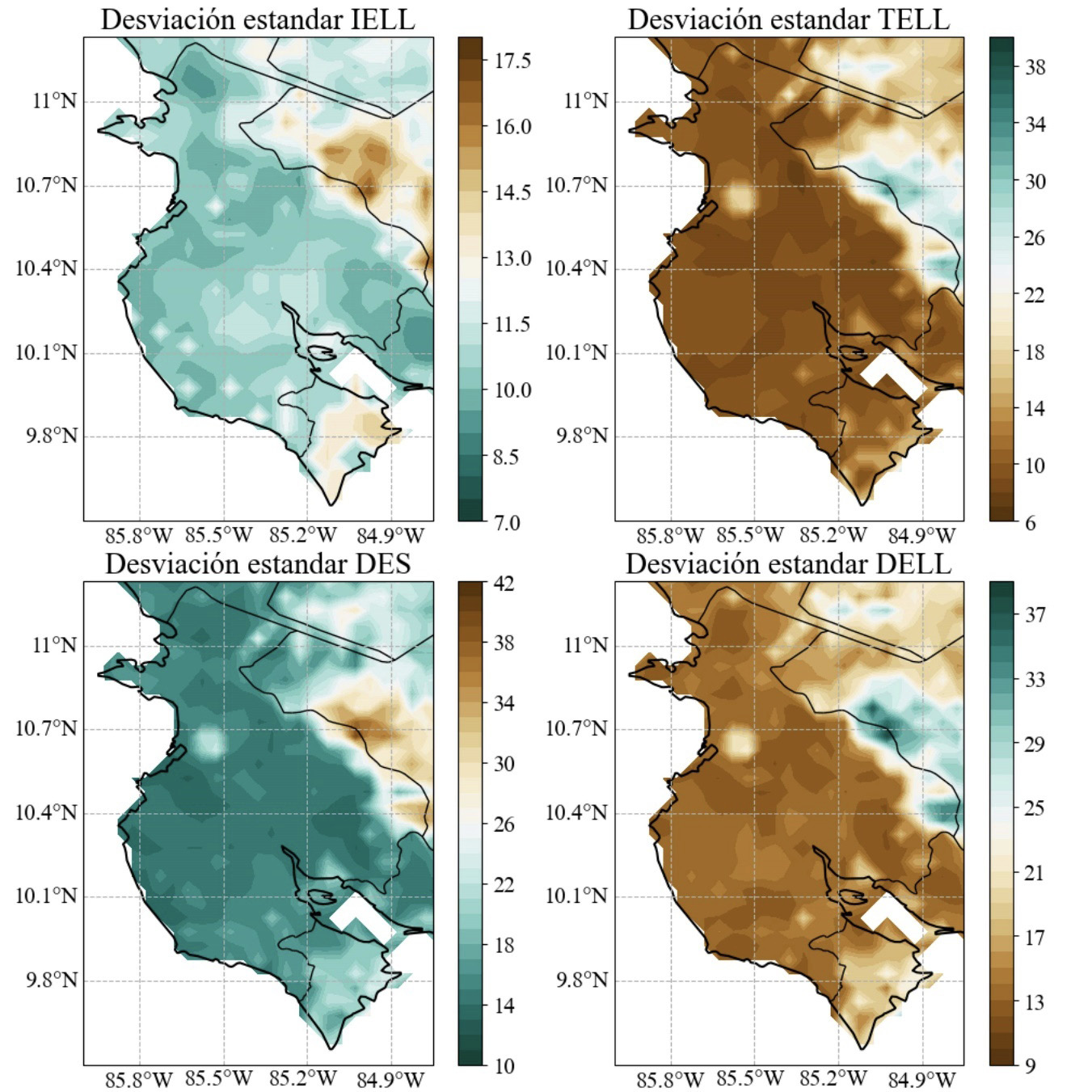
Figura 3. Desviación estándar para las series de IELL, TELL, DES y DELL de la base de datos de ERA5+CHIRPS en la región de Guanacaste para el periodo 1950-2020.

Por otro lado, la época seca y lluviosa muestran comportamientos uniformes en todo Guanacaste con las condiciones más secas al norte (unos 190 días para la DES y 174 para la DELL) y más húmedas al sur y oeste (unos 177 días para la DES y 190 para la DELL), lo que indica un comportamiento muy simétrico entre la DES y DELL.

La desviación estándar y rango inter cuartil (figura 3 y figura 4) rondan las dos semanas en prácticamente toda la región, con las dispersiones más altas fuera de la región de estudio, aunque abarcando una pequeña zona del cantón de Tilarán.

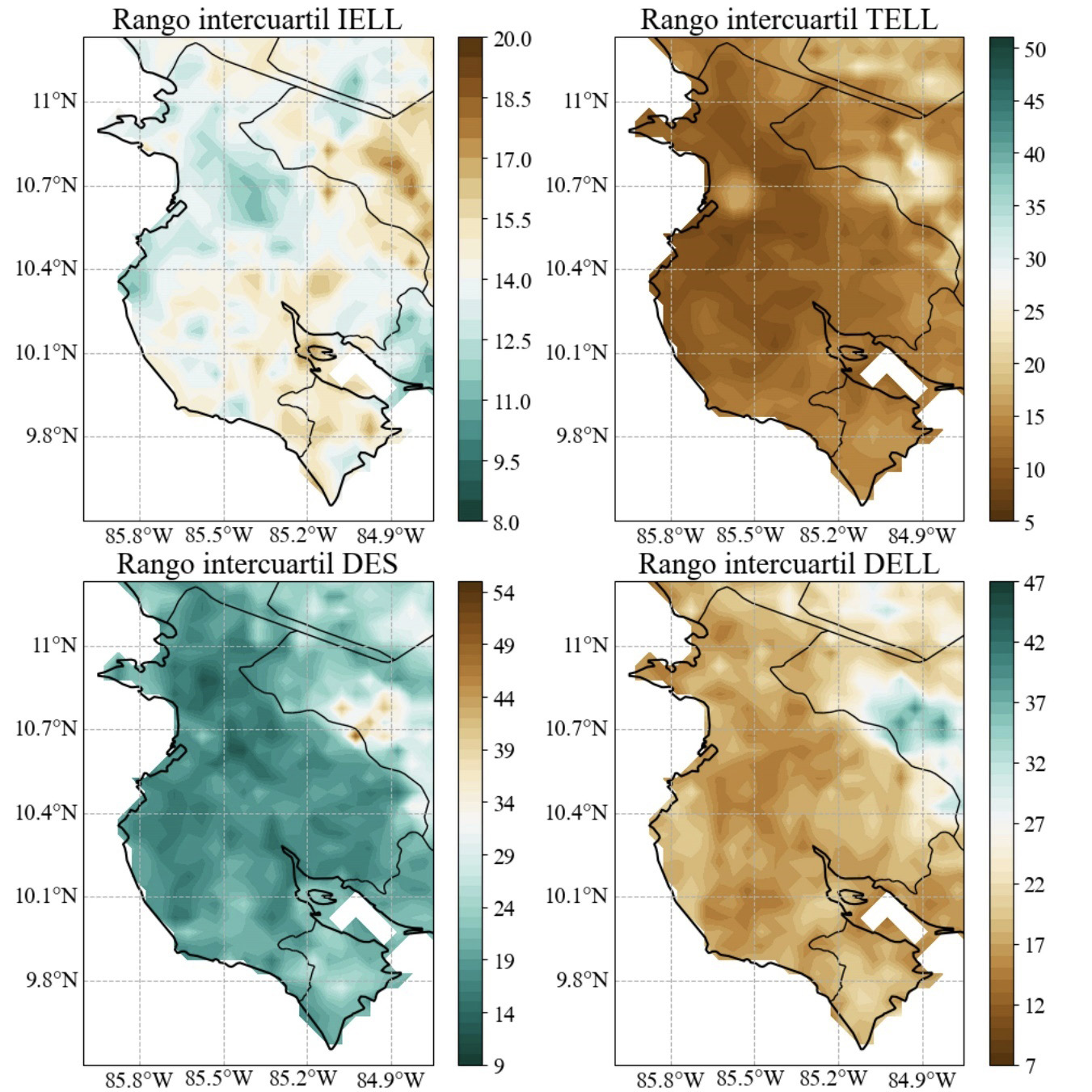
Figura 4. Rango Inter cuartil para las series de IELL, TELL, DES y DELL de la base de datos de ERA5+CHIRPS en la región de Guanacaste para el periodo 1950-2020.

Con respecto a las tendencias (figura 5) estas indican que tanto se atrasan o adelantan el IELL, TELL, DES y DELL, por ejemplo, una tendencia de -0.50 en el TELL implica un adelanto de medio día por cada año transcurrido para que ocurra el TELL. En general las tendencias muestran condiciones húmedas en prácticamente toda la región, implicando inicios tempranos de la estación lluviosa y términos tardíos, disminuyendo la duración de la estación seca, aunque se aprecia una zona al norte hacia condiciones secas en todas las fechas.

El cuadro 1 presenta un resumen numérico para las figuras 2, 3, 4 y 5 usando los percentiles 25, 50 y 75 (P25, P50 y P75, respectivamente), permitiendo una visualización clara de los valores medios de cada figura y los umbrales entre los cuales se encuentra el 50% de los datos en cada fecha (IELL, TELL, DES, DELL) de la región.

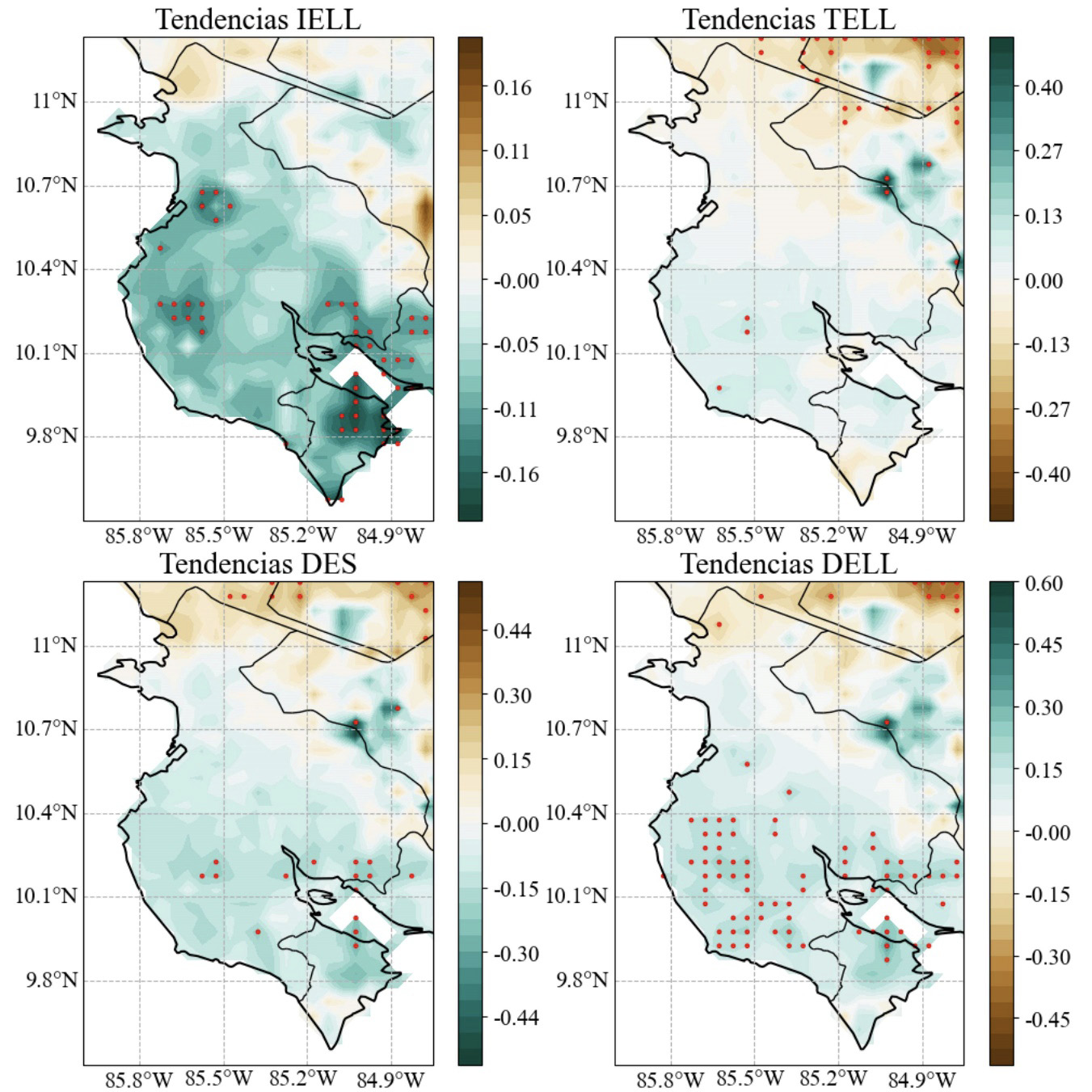
Figura 5. Tendencias para las series del IELL, TELL, DES y DELL de la base de datos de ERA5+CHIRPS en la región de Guanacaste para el periodo 1950-2020 con unidades de día año-1. Los puntos rojos representan zonas con significancia estadística del 95% (α < 0.05).

Cuadro 1. Valores de los percentiles 25, 50 y 75 para el IELL, TELL, DES y DELL para los estadísticos: mediana, desviación estándar, rango inter cuartil y tendencias de ERA5+CHIRPS.

Parámetros	IELL			TELL			DES			DELL
	P25	P50	P75	P25	P50	P75	P25	P50	P75	P25	P50	P75
Mediana	129	132	136	310	311	313	183	186	189	176	180	184
Desviación estándar	10,1	10,7	11,8	9,1	9,8	15,4	14,5	15,6	20,4	13,2	14,3	19,0
Rango inter cuartil	13,3	14,0	15,0	11,0	13,0	15,0	17,5	19,8	22,5	16,5	18,0	21,0
Tendencias	-0,09	-0,06	-0,01	-0,05	0,00	0,05	-0,12	-0,06	0,04	-0,02	0,08	0,13

Al determinar las CP sobre los datos de ERA5+CHIRPS, se encontró que la CP1 representa la gran mayoría de la varianza en la región y muestra una alta correlación en la provincia de Guanacaste, mientras la CP2 explica una varianza bastante inferior a la CP1 (cuadro 2).

Cuadro 2. Porcentaje de la variabilidad explicada por la CP1 y CP2 asociada al IELL, TELL, DELL y DES.

% de variabilidad explicada	IELL	TELL	DES	DELL
CP 1	72.13	45.00	59.85	53.59
CP 2	7.81	11.01	7.84	7.16

Cuadro 3. Correlación de Pearson entre la CP1 asociada al IELL, TELL, DES y DELL y los índices ATN, N3.4, ATN-N3.4 y CLLJ en su respectivo periodo.

Índices	Correlación de Pearson CP1	Índices	Correlación de Pearson CP1
ATN vs IELL	-0,17	ATN-N3.4 vs IELL	-0,25
ATN vs TELL	0,04	ATN-N3.4 vs TELL	0,23
ATN vs DES	-0,12	ATN-N3.4 vs DES	-0,31
ATN vs DELL	0,19	ATN-N3.4 vs DELL	0,37
N3.4 vs IELL	0,11	CLLJ vs IELL	0,36
N3.4 vs TELL	-0,25	CLLJ vs TELL	-0,41
N3.4 vs DES	0,23	CLLJ vs DES	0,28
N3.4 vs DELL	-0,30	CLLJ vs DELL	-0,41

*Los valores en negrita representan significancia estadística al 99% y en itálica al 95% (α < 0.01 y 0.05, respectivamente).

El cuadro 3 muestra las correlaciones de Pearson entre los diferentes índices de variabilidad climática (N3.4, ATN, N3.4-ATN y CLLJ) y la CP1 asociada al IELL, TELL, DELL y DES. Como se puede apreciar no existe correlación significativa en ningún caso para el ATN. El índice N3.4 muestra correlaciones negativas significativas contra el TELL y DELL. El índice ATN-N3.4 muestra correlaciones significativas (a excepción del TELL) que coinciden a los ya obtenidos con CHIRPS por [10] indicando que un calentamiento relativo del Atlántico con respecto al Pacífico ecuatorial favorece que las lluvias inicien antes, que la estación seca sea más corta y la lluviosa más larga, por tanto, un enfriamiento de los océanos favorece condiciones contrarias. En el caso de la CLLJ su comportamiento es inverso al del ATN-N3.4.

Cuadro 4. Tablas de contingencia de las probabilidades empíricas condicionales (%) para la CP1 de la DELL de ERA+CHIRPS según los índices ATN-N3.4 (arriba) y CLLJ (abajo), promediados de mayo a octubre, M-0. Los valores entre paréntesis son las frecuencias empíricas absolutas y las categorías usadas son bajo lo normal (BN), neutral (N) y arriba de lo normal (AN), separadas por los percentiles 33 y 67, mostrados en los paréntesis en negrita.

		DELL
		BN (<-5.94)	N	AN (>5.53)
ATN-N34 (M-O) χ2=14.77 (0.98)	BN (<-0.42)	63(15)***	21(5)**	17(4)***
	N	22(5)**	43(10)*	35(8)
	AN (>0.58)	17(4)***	33(8)	50(12)***
CLLJ (M-O) χ2=11.45 (0.98)	BN (<1.84 ms-1)	13(3)***	33(8)	54(13)***
	N	35(8)	39(9)	26(6)*
	AN (>2.48 ms-1)	54(12)***	25(6)	21(5)**

* Significancia estadística al 90% (α < 0.10).
** Significancia estadística al 95% (α < 0.05).
*** Significancia estadística al 99% (α < 0.01).

El cuadro 4 muestra los resultados del análisis de contingencia destacando solo las correlaciones entre la DELL y los índices ATN-N3.4 y la CLLJ dada la significancia estadística. Con respecto a la tabla de contingencia entre la DELL y ATN-N3.4 las categorías más probables son (BN, BN), (N, N) y (AN, AN) sugiriendo que un ATN-N3.4 bajo lo normal es más probable que propicie una DELL más corta, un ATN-N3.4 normal implica una DELL dentro lo normal y una ATN-N3.4 arriba de lo normal es probable que propicie una DELL larga. Por otro lado, la tabla de contingencia entre la DELL y la CLLJ muestra un comportamiento contrario donde las categorías más probables son (BN, AN), (N, N) y (AN, BN), esto implica que una CLLJ bajo lo normal (arriba de lo normal) propicia una DELL más larga, condiciones normales de la CLLJ sugieren DELL normales y una CLLJ arriba de lo normal es probable que propicie DELL cortas.

Conclusiones

La alta resolución de los datos de CHIRPS y ERA5 con reducción de escala usados en la provincia de Guanacaste, permitieron caracterizar la época seca y lluviosa determinando las fechas del IELL, el TELL, la DES y la DELL para el periodo 1950-2020 (71 años), lo cual hace más robustos los resultados climatológicos.

En forma similar a los resultados obtenidos por [10] usando los datos de CHIRPS para un periodo más corto, con los datos usados de CHIRPS+ERA5 sobre Guanacaste, se encontró que las fechas del IELL ocurren más temprano en cantones centrales de Guanacaste alrededor de la desembocadura del Tempisque, donde las fechas son cada vez más tardías al desplazarse hacia regiones costeras y limítrofes con Alajuela, alcanzado los IELL más tardíos al norte de la provincia en el cantón de La Cruz, sugiriendo una dependencia latitudinal para el IELL como se ha visto en otros trabajos [1], [3], pero al tratarse de una región tan pequeña no es posible asegurar que tal comportamiento se mantenga.

Por otro lado, las fechas del TELL presentan valores más tardíos al sur y oeste de la región, mientras los valores más tempranos en la zona central y norte de Guanacaste. Además, se debe resaltar la alta uniformidad del TELL, ya que como se aprecia del cuadro 1 la diferencia entre su P25 y P75 es de tan solo 3 días por lo que la gran mayoría de los datos tienen baja dispersión en Guanacaste, lo que podría sugerir que no hay dependencia latitudinal para el TELL, pero al igual que el IELL al tratarse de una región tan pequeña es difícil asegurar que el comportamiento se mantenga geográficamente.

Con respecto a la DES y DELL, su comportamiento es bastante uniforme en gran parte de la región con las condiciones más secas al norte y las más húmedas al sur de la península de Nicoya y al área limítrofe entre Guanacaste y Puntarenas, además el periodo entre ambas duraciones es bastante simétrico, donde aproximadamente una mitad del año exhibe una estación seca y la otra estación lluviosa, aunque esto varía un poco en las regiones más secas y húmedas de la provincia.

Los cuatro índices muestran tendencias consistentes espacialmente, aunque en general no estadísticamente significativas, hacia condiciones húmedas en los tres conjuntos de datos, lo que indica que se esperan IELL más tempranos, TELL más tardíos, DES más cortas y DELL más largas, lo que coincide con [10] al usar solo el conjunto de CHIRPS para el periodo 1981-2020. Sin embargo, solo destaca significativamente al 95% (α < 0.05) una pequeña zona en el cantón de Abangares en el IELL y DELL (con unos pocos puntos en rejilla de la DES), otra sobre una pequeña parte de Liberia y Santa Cruz en el caso del IELL, para el DELL esta zona es más amplia y abarca casi todos los cantones al sur de Guanacaste, aunque no sobre Liberia, y finalmente una zona en la provincia de Puntarenas ubicada sobre la península de Nicoya en el caso del IELL y DELL, difiriendo con los resultados de [10] en la distribución de las zonas significativas.

El análisis de CP resultó en algunas correlaciones significativas entre los índices de variabilidad climática y la CP1 asociada al IELL, TELL, DES y DELL en los datos de ERA5+CHIRPS para los 71 años considerados, donde se destaca principalmente las correlaciones debidas al ATN-N3.4 y la CLLJ. Estas implican que un índice del ATN-N3.4 positivo (negativo) favorece las condiciones húmedas (secas), mientras la CLLJ muestra un comportamiento inverso, esto posiblemente esté ligado al movimiento latitudinal de la ZCIT y los eventos convectivos en la región influenciados por las condiciones del océano Atlántico, océano Pacífico y la intensidad de la CLLJ como se ha visto en diversos trabajos [1], [7], [20], [29]. Además estas correlaciones son similares a las obtenidas por [10] usando los datos CHIRPS y el índice OMA en lugar del ATN para los años 1981-2020.

Por su parte la correlación entre la CP1 asociada al IELL, TELL, DES y DELL del conjunto de datos ERA5+CHIRPS y los índices de variabilidad climática, muestra resultados similares a los que se obtienen usando únicamente CHIRPS [10], aunque con menor significancia en los índices oceánicos (ATN-N3.4 principalmente). Según [10], esto posiblemente se deba a que por separado los datos de ERA5 presenten menor o poca correlación contra los índices oceánicos. De modo que las correlaciones significativas del conjunto de datos ERA5+CHIRPS se debe principalmente a la contribución de los datos de CHIRPS, esto podría indicar que el reanálisis de ERA5 o el método de reducción de escala aplicado no son capaces de representar la variabilidad asociada a los océanos, aunque si la de la CLLJ (al menos para el IELL y TELL). Sin embargo, se deben tener en consideración los alcances de ERA5, este conjunto tiene originalmente una baja resolución comparado con la de CHIRPS, razón por la cual se aplicó el método de CA sobre los mismos y Guanacaste es una región con cierta complejidad orográfica debido a su diversidad en suelos y a la presencia de pequeños cerros dispersos en la provincia, así como la presencia de diversos cuerpos de agua e importantes humedales, de modo que la interacción de estos factores y las condiciones atmosféricas pueden ser más complejas y no capturadas por el reanálisis o el método de CA.

En esta investigación se encontró concordancia entre ERA5 y CHIRPS en términos climatológicos (ver figura A1 y cuadro A1 y A2 incluidos en el Anexo), pero no en las correlaciones de variabilidad climática contra índices oceánicos (ATN y N3.4), por lo que se debería trabajar también con datos de ERA5 que abarquen un periodo común con datos de estaciones meteorológicas o CHIRPS que ya se ha mostrado que representa bien la región [10], [30]. Lo anterior también permitiría comparar los datos de ERA5 con reducción de escala contra fuentes de variabilidad climática en el periodo de 1981-2020 para verificar si estos logran capturar la variabilidad climática asociada a los océanos como hace CHIRPS, ya que no fue posible determinar si ERA5 no explica de manera eficiente la variabilidad oceánica de la región debido a la propia base de datos, al método de reducción de escala aplicado de CA o al periodo utilizado.

Agradecimientos

Agradecemos a los proyectos B9454 (Fondo de Grupos), C3991 (UCREA), A1715, B0810, A5719, C2103, C3721 y A4906 (PESCTMA) inscritos a la Universidad de Costa Rica dentro de los cuales se enmarca este trabajo y del apoyo brindado por el Centro Internacional de Investigaciones para el Desarrollo (IDRC), Ottawa, Canadá y el Consejo Superior Universitario Centroamericano (CSUCA) al proyecto RC4 (C4-468, CR-66, SIA 0054-23). Las opiniones aquí expresadas no representan necesariamente las del IDRC, CSUCA o las de la Junta de Gobernadores.

El autor Hugo Hidalgo revisó este artículo cuando se encontraba en licencia sabática de la Universidad de Costa Rica.

Referencias

[1] E. Alfaro, «Some Characteristics of the Annual Precipitation Cycle in Central America and their Relationships with its Surrounding Tropical Oceans», Tópicos Meteorológicos Ocean., vol. 9, n.o 2, Art. n.o 2, 2002, doi: www.kerwa.ucr.ac.cr/handle/10669/15428.

[2] S. G. Díaz, «Inicio de las lluvias de verano en las costas del Pacífico Mesoamericáno». [Tesis de licenciatura, Universidad Nacional Autónoma de México], 2019. [En línea]. Disponible en: https://repositorio.unam.mx/contenidos/3466119

[3] R. H. Gramzow y W. K. Henry, «The Rainy Pentads of Central America», J. Appl. Meteorol. Climatol., vol. 11, n.o 4, Art. n.o 4, jun. 1972, doi: 10.1175/1520-0450(1972)011<0637:TRPOCA>2.0.CO;2.

[4] J. A. Amador, «A Climate Feature of the Tropical Americas: The Trade Wind Easterly Jet», Rev. Tópicos Meteorológicos Oceonográficos, vol. 5, n.o 2, Art. n.o 2, jun. 1998.

[5] J. A. Amador, «The Intra-Americas Sea low-level jet: overview and future research», Ann. N. Y. Acad. Sci., vol. 1146, pp. 153-188, dic. 2008, doi: 10.1196/annals.1446.012.

[6] D. Enfield y E. Alfaro, «The Dependence of Caribbean Rainfall on the Interaction of the Tropical Atlantic and Pacific Oceans», J. Clim., vol. 12, n.o 7, Art. n.o 7, jul. 1999, doi: 10.1175/1520-0442(1999)012<2093:TDOCRO>2.0.CO;2.

[7] H. G. Hidalgo, A. M. Durán‐Quesada, J. A. Amador, y E. Alfaro, «The Caribbean Low‐Level Jet, the Inter‐Tropical Convergence Zone and precipitation patterns in the Intra‐Americas Sea: A proposed dynamical mechanism», Geogr. Ann. Ser. Phys. Geogr., vol. 97, n.o 1, Art. n.o 1, mar. 2015, doi: 10.1111/geoa.12085.

[8] P. Ureña-Mora y E. Alfaro, «Comparación de métodos de detección del inicio y término de la estación lluviosa basado en datos de precipitación (Comparison of detection methods for the onset and demise of the rainy season based on precipitation)», Rev. Tecnológica En Marcha, 2022, doi: https://doi.org/10.18845/tm.v35i4.5778.

[9] R. J. Bombardi, K. V. Pegion, J. L. Kinter, B. A. Cash, y J. M. Adams, «Sub-seasonal Predictability of the Onset and Demise of the Rainy Season over Monsoonal Regions», Front. Earth Sci., vol. 5, 2017, doi: 10.3389/feart.2017.00014.

[10] K. Ugalde, «Estudio del inicio y término de la estación lluviosa en el Pacífico Norte de Costa Rica en el periodo 1950-2020», Tesis de licenciatura aprobada con distinción sobresaliente, Universidad de Costa Rica, 2022. [En línea]. Disponible en: https://hdl.handle.net/10669/89114

[11] C. Funk et al., «The climate hazards infrared precipitation with stations—a new environmental record for monitoring extremes», Sci. Data, vol. 2, n.o 1, Art. n.o 1, dic. 2015, doi: 10.1038/sdata.2015.66.

[12] D. B. Enfield, A. M. Mestas-Nuñez, y P. J. Trimble, «The Atlantic Multidecadal Oscillation and its relation to rainfall and river flows in the continental U.S.», Geophys. Res. Lett., vol. 28, n.o 10, pp. 2077-2080, 2001, doi: 10.1029/2000GL012745.

[13] S. B. Goldenberg, C. W. Landsea, A. M. Mestas-Nuñez, y W. M. Gray, «The Recent Increase in Atlantic Hurricane Activity: Causes and Implications», Science, vol. 293, n.o 5529, pp. 474-479, jul. 2001, doi: 10.1126/science.1060040.

[14] J. A. Amador y E. J. Alfaro, «Métodos de reducción de escala: aplicaciones al tiempo, clima, variabilidad climática y cambio climático», Rev. Iberoam. Econ. Ecológica, n.o 11, pp. 39-52, 2009.

[15] T. Maldonado, E. J. Alfaro, J. A. Amador, y A. Rutgersson, «Regional precipitation estimations in Central America using the Weather Research and Forecast model», Rev. Biol. Trop., vol. 66, n.o 1, pp. S231-S254, 2018, doi: https://doi.org/10.15517/rbt.v66i1.33303.

[16] H. G. Hidalgo, E. J. Alfaro, y P. M. Pérez-Briceño, «Cambios climáticos proyectados de modelos CMIP5 en La Cruz, Guanacaste, Costa Rica», Rev. Biol. Trop., vol. 69, pp. 60-73, oct. 2021, doi: 10.15517/rbt.v69is2.48307.

[17] H. G. Hidalgo, M. Dettinger, y D. Cayan, «Downscaling With Constructed Analogues: Daily Precipitation and Temperature Fields Over The United States», California Energy Commission PIER Final Project Report CEC-500-2007-123, 2008. Accedido: 20 de enero de 2022. [En línea]. Disponible en: https://www.semanticscholar.org/paper/Downscaling-With-Constructed-Analogues%3A-Daily-and-Le%C3%B3n-Dettinger/2ccaf3294385bc206b751c466b4d6e2ceecf70af

[18] H. Hersbach et al., «The ERA5 global reanalysis», Q. J. R. Meteorol. Soc., vol. 146, n.o 730, Art. n.o 730, 2020, doi: https://doi.org/10.1002/qj.3803.

[19] J. A. Amador, E. J. Alfaro, E. R. Rivera, y B. Calderón, «Climatic Features and Their Relationship with Tropical Cyclones Over the Intra-Americas Seas», en Hurricanes and Climate Change: Volume 2, J. B. Elsner, R. E. Hodges, J. C. Malmstadt, y K. N. Scheitlin, Eds., Dordrecht: Springer Netherlands, 2010, pp. 149-173. doi: 10.1007/978-90-481-9510-7_9.

[20] E. Alfaro, L. Cid, y D. Enfield, «Relaciones entre el inicio y el término de la estación lluviosa en Centroamérica y los océanos Pacífico y Atlántico tropical», Investig. Mar., vol. 26, pp. 59-69, 1998, doi: 10.4067/S0717-71781998002600006.

[21] B. Fallas y E. Alfaro, «Uso de herramientas estadísticas para la predicción estacional del campo de precipitación en América Central como apoyo a los Foros Climáticos Regionales. 1: Análisis de tablas de contingencia.», Rev. Climatol., vol. 12, pp. 61-79, nov. 2012.

[22] D. Poleo, E. Solano León, y W. Stolz, «La Oscilación atmosférica Madden-Julian (MJO) y las lluvias en Costa Rica», Tópicos Meteorológicos Ocean., vol. 13, p. 58, jun. 2014.

[23] K. E. Trenberth y D. P. Stepaniak, «Indices of El Niño Evolution», J. Clim., vol. 14, n.o 8, Art. n.o 8, abr. 2001, doi: 10.1175/1520-0442(2001)014<1697:LIOENO>2.0.CO;2.

[24] K. H. Cook y E. K. Vizy, «Hydrodynamics of the Caribbean Low-Level Jet and Its Relationship to Precipitation», J. Clim., vol. 23, n.o 6, pp. 1477-1494, mar. 2010, doi: 10.1175/2009JCLI3210.1.

[25] D. S. Wilks, Statistical Methods in the Atmospheric Sciences, 4.a ed. Elsevier Science, 2019.

[26] W. McKinney, «Data Structures for Statistical Computing in Python», presentado en Proceedings of the 9th Python in Science Conference, ene. 2010, pp. 56-61. doi: 10.25080/Majora-92bf1922-00a.

[27] C. R. Harris et al., «Array programming with NumPy», Nature, vol. 585, n.o 7825, Art. n.o 7825, sep. 2020, doi: 10.1038/s41586-020-2649-2.

[28] E. Alfaro, F. J. Soley, y D. Enfield, Uso de una Tabla de Contingencia para Aplicaciones Climáticas (Use of a Contingency Table for Climatic Applications). Guayaquil, Ecuador: ESPOL y FUNDESPOL, 2004. Accedido: 3 de marzo de 2021. [En línea]. Disponible en: http://www.kerwa.ucr.ac.cr/handle/10669/76751

[29] E. Quirós y H. G. Hidalgo, «Variabilidad y conexiones climáticas de la zona de convergencia intertropical del Pacífico Este», Rev. Tópicos Meteorológicos Ocean., vol. 15, n.o 1, Art. n.o 1, jul. 2016.

[30] L. Quesada-Hernandez, «Respuesta de la hidrología superficial de la cuenca del río Tempisque a la variabilidad climática y cambio de cobertura de la tierra», 2019. doi: 10.13140/RG.2.2.22256.20485.

Anexos

La figura A1 representa el promedio de precipitación diaria en el periodo de 1950-1980 en caso de los datos de ERA5 con reducción de escala y de 1981-2020 en caso de los datos de CHIRPS.

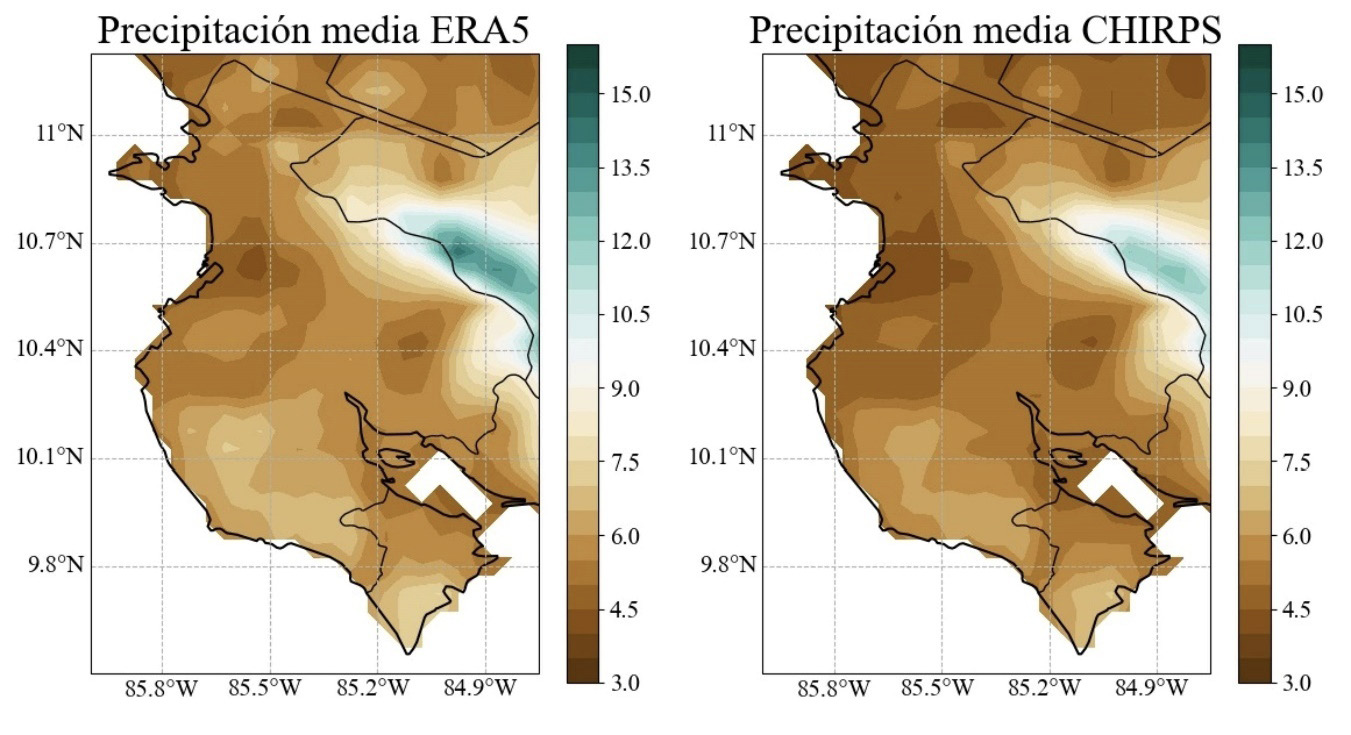
Figura A1. Precipitación media diaria (mm∙día-1) para los datos de ERA5 con reducción de escala, izquierda, (1950-1980) y CHIRPS, derecha (1981-2020).

Al aumentar la resolución de los datos de ERA5 por medio del ajuste de escala para que coincidan con la resolución de CHIRPS, se obtuvieron resultados que representan bien la región de Guanacaste en términos climatológicos. Ugalde [10] validó que los datos de CHIRPS capturan correctamente las precipitaciones en la región, por lo que es posible validar ERA5 usando CHIRPS. Ambos conjuntos de datos muestran los mismos núcleos de bajas precipitaciones (por ejemplo, los que se encuentran alrededor del cantón de Cañas y Liberia), también se observa un núcleo de altas precipitaciones al norte de la cordillera de Guanacaste, aunque este se escapa de la región de estudio. Los percentiles 25, 50, y 75 de los datos de ERA5 en la figura A1 son P25 = 5.31 mm∙día-1, P50 = 5.75 mm∙día-1 y P75 = 6.61 mm∙día-1, mientras que para el caso de CHIRPS son P25 = 4.73 mm∙día-1, P50 = 5.16 mm∙día-1 y P75 = 5.96 mm∙día-1 indicando que CHIRPS presenta menores precipitaciones. De los datos que componen la figura A1 se calculó el EMA y el índice KGE obteniendo valores de 0.65 mm∙día-1 y 0.88 respectivamente, indicando que ambos mapas coinciden adecuadamente entre sí. Sin embargo, es conveniente realizar la comparativa con periodos iguales en ambos conjuntos de datos, lo que permitiría calcular métricas para validar los resultados como la correlación de Pearson, el EMA o el índice KGE.

Cuadro A1. Valores de los percentiles 25, 50 y 75 para el IELL, TELL, DES y DELL para los estadísticos: mediana, desviación estándar, rango inter cuartil y tendencias para ERA5.

Parámetros	IELL			TELL			DES			DELL
	P25	P50	P75	P25	P50	P75	P25	P50	P75	P25	P50	P75
Mediana	131	133	138	308	311	315	185	188	190	176	179	182
Desviación estándar	9,9	10,6	12,14	9,0	9,9	11,3	12,9	14,9	17,3	12,5	14,0	16,6
Rango inter cuartil	12,5	13,8	14,8	12,0	15,0	17,0	16,0	18,5	21,5	16,5	18,5	20,5
Tendencias	-0,21	-0,14	-0,05	0,10	0,22	0,33	-0,38	-0,22	-0,05	0,24	0,36	0,50

En la cuadro A1 se presenta un resumen numérico para los P25, P50 y P75, lo que ayuda a visualizar más claramente el comportamiento medio del IELL, TELL, DES y DELL para los estadísticos: mediana, desviación estándar, rango inter cuartil y tendencias para ERA5 y los umbrales entre los cuales se encuentra cada índice para el 50% de la región, en general mostrando un comportamiento similar al de CHIRPS [10]. Las tendencias de los cuatro índices de ERA5 muestran también un comportamiento similar a CHIRPS, hacia condiciones húmedas, sin embargo, según Ugalde [10], las regiones significativas difieren en ambos conjuntos de datos, y para ERA5 solo se pueden considerar relevantes el TELL y DELL. Las regiones significativas del TELL abarcan varios cantones en la región este de la provincia y este del golfo de Papagayo, mientras que las significancias de la DELL también abarcan las regiones anteriores solo que cubren un área un poco más amplia.

Cuadro A2. Comparaciones entre los estadísticos del IELL, TELL, DES y DELL calculados con CHIRPS y ERA5, usando el EMA, rS y KGE.

Parámetros	IELL			TELL			DES			DELL
	EMA	rS	KGE	EMA	rS	KGE	EMA	rS	KGE	EMA	rS	KGE
Mediana	2,36	0,93	0,77	2,75	0,46	0,46	4,17	0,77	0,66	4,18	0,76	0,68
Desviación estándar	1,39	0,39	0,40	3,03	0,53	0,64	3,56	0,45	0,51	3,31	0,45	0,64
Rango inter cuartil	2,27	-0,29	-0,31	4,55	0,51	0,20	4,06	0,36	0,35	4,70	0,02	0,12
Tendencias	0,11	0,46	-0,56	0,26	-0,05	-3,61	0,27	0,16	-0,05	0,27	0,05	-0,10

* En la correlación de Spearman valores en negrita representan significancia estadística al 99% (α < 0.01).

En el cuadro A2 se presentan una comparación entre los estadísticos obtenidos con CHIRPS y los respectivos a ERA5. En términos climatológicos se puede apreciar que la mediana de ambos conjuntos de datos se corresponde bastante bien entre sí, en general con EMA bajos en los cuatro índices, además de rS y KGE positivos (rS significativo al 99%). La desviación estándar también se corresponde bien en los cuatro índices, mostrando valores de dispersión bastante similares entre ambos conjuntos. Sin embargo, para el rango inter cuartil este no es el caso, tanto el TELL como la DES muestran una correspondencia entre ERA5 y CHIRPS, pero el IELL y DELL no, el IELL muestra EMA bajos con un rS y KGE negativos, mientras que en la DELL tanto la rS y KGE son muy cercanos a cero. Para las tendencias el único caso que se puede resaltar es el rS del IELL positivo (significativo) el resto de los índices muestran correlaciones muy bajas o incluso negativas.

En general la correspondencia entre CHIRPS y ERA5 es bastante buena para los índices del IELL, TELL, DES y DELL en el caso de la mediana, media (no mostrada, pero con resultados muy similares a la mediana) y desviación estándar, sin embargo, no sucede lo mismo en todos los casos del rango inter cuartil y para las tendencias solo se tiene un caso significativo a resaltar.

Declaración sobre uso de Inteligencia Artificial (IA)

Los autores aquí firmantes declaramos que no se utilizó ninguna herramienta de IA para la conceptualización, traducción o redacción de este artículo.

---

1. 1 Universidad Estatal a Distancia, Escuela de Ciencias Exactas y Naturales. Costa Rica.
   kugaldec@uned.ac.cr
   https://orcid.org/0000-0002-9762-9811

2. 2 Universidad de Costa Rica, Centro de Investigaciones Geofísicas (CIGEFI), Centro de Investigación en Ciencias del Mar y Limnología (CIMAR), Escuela de Física, San Pedro, San José, Costa Rica.
   erick.alfaro@ucr.ac.cr
   https://orcid.org/0000-0001-9278-5017

3. 3 Universidad de Costa Rica, Centro de Investigaciones Geofísicas (CIGEFI), Centro de Investigación en Matemática Pura y Aplicada (CIMPA), Escuela de Física, San Pedro, San José, Costa Rica.
   hugo.hidalgo@ucr.ac.cr
   https://orcid.org/0000-0003-4638-0742

4. 4 Universidad de Costa Rica, Centro de Investigaciones Geofísicas (CIGEFI), San Pedro, San José, Costa Rica.
   tito.maldonado@ucr.ac.cr
   https://orcid.org/0000-0001-9774-9082