Comparative analysis of traditional methods and a deep learning approach for multivariate imputation of missing values in the meteorological field

Análisis comparativo de algoritmos tradicionales y un modelo de aprendizaje profundo para la imputación multivariada de valores faltantes en el campo meteorológico

Ana Cristina Arias-Muñoz1, Susana Cob-García2, Luis-Alexander Calvo-Valverde3

Fecha de recepción: 21 de julio, 2023
Fecha de aprobación: 18 de octubre, 2023

Arias-Muñoz, A.C; Cob-García, S; Calvo-Valverde, L.A. Comparative analysis of traditional methods and a deep learning approach for multivariate imputation of missing values in the meteorological field. Tecnología en Marcha. Vol. 37, No 3. Julio-Setiembre, 2024. Pág. 33-47

https://doi.org/10.18845/tm.v37i2.6746

Keywords

Data imputation; EMB; MissForest; LSTM; time series.

Abstract

Climate observations are the groundwork for several real-world applications such as weather forecasting, climate change monitoring and environmental impact assessments. However, the data is mostly measured and recorded by external devices exposed to numerous variables, causatives of malfunctions and, therefore, missing values. Nowadays, data imputation in the time series field has been researched in depth and a wide variety of methods have been proposed, where traditional classification and regression algorithms predominate, even though there are also deep learning approaches that manage to capture temporal relationships between observations. In this article, a comparative analysis between a classification imputation algorithm, a regression imputation algorithm, and a deep learning imputation model is made: MissForest algorithm, based on random trees; Expectation Maximization with Bootstrap (EMB), the maximum likelihood estimation algorithm; and a proposed deep learning model, based on the Long-Short Term Memory (LSTM) architecture. Data from the Costa Rica meteorological field were used, which consist of multivariate data coming from several weather stations in the same geographical area.

Palabras clave

Imputación de datos; EMB; MissForest; LSTM; series de tiempo.

Resumen

Las observaciones climáticas son la base para varias aplicaciones del mundo real, como el pronóstico del tiempo, el monitoreo del cambio climático y las evaluaciones de impacto ambiental. Sin embargo, la mayoría de los datos son medidos y registrados por dispositivos externos expuestos a numerosas variables, causantes de mal funcionamiento de los dispositivos y, por lo tanto, de los valores faltantes. En la actualidad, se ha investigado en profundidad la imputación de datos en el campo de las series temporales y se han propuesto una gran variedad de métodos, donde predominan los algoritmos tradicionales de clasificación y regresión, no obstante, también existen enfoques de aprendizaje profundo que logran capturar relaciones temporales entre observaciones. En este artículo se realiza un análisis comparativo entre un algoritmo de clasificación, un algoritmo de regresión y un modelo de aprendizaje profundo: algoritmo MissForest, basado en árboles aleatorios; Expectation Maximization with Bootstrap (EMB), el algoritmo de estimación de máxima verosimilitud; y una propuesta de un modelo de aprendizaje profundo, basado en la arquitectura Long-Short Term Memory (LSTM). Se utilizaron datos del campo meteorológico de Costa Rica, los cuales consisten en datos multivariados provenientes de varias estaciones meteorológicas en una misma zona geográfica.

Introduction

In the field of time series, missing data is a common problem and, at the same time, it’s difficult to solve. Missing data can be a result of multiple reasons: noisy data, chaotic signals, network communication failures, sensor maintenance problems, damage to observation equipment, etc.

Among the options researchers have used to solve the missing data problem are data interpolation and data imputation. Both solutions seek to fill in or “guess” those missing data using the available information. By using statistical methods for imputation, good estimates can be obtained from uncollected data when the time series have a small number of gaps. However, it’s difficult to predict consecutive data in time series [1].

Filling in missing data in time series usually involves some assumptions, but data should be imputed as precisely as possible to avoid data distortions that can lead to flawed or undesirable results, including inaccurate predictions depending on the use cases or problems in the decision-making process for policy formulation [2]. Most of the best performing standard algorithms for data imputation rely on correlations between attributes to estimate missing data values.

Since the mid-1980s, sophisticated imputation methods have been introduced, including expectation maximization (EM), weight estimation methods, K-Nearest Neighbors, multiple imputation, and Bayesian imputation.

The current research focuses on the Expectation Maximization with Bootstrap (EMB) and MissForest (Random Forests for missing data) algorithms, and a proposed LSTM neural network. An evaluation and comparison of the aforementioned imputation methods is carried out in regards to their performance in the multiple and multivariate imputation of time series, with data from the Costa Rican climatology area.

One of the advantages of using machine learning is that they are usually more flexible than standard statistical models, as they can capture high-order interactions between data, resulting in better predictions. Deep learning methods hold great promise for time series forecasting, namely machine learning of time dependency and automatic handling of time structures such as trends and seasonality [3].

To successfully execute a comparative analysis and performance evaluation, we used the metrics Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Coefficient of determination (R2) and execution time (time the algorithm or model takes to complete the data imputation process). For the execution time of the model, training time is not considered.

In this paper, we will refer to season or weather station as a specific area or zone that has been used to obtain, measure and process data from the different meteorological phenomena that occur in the atmosphere. This research proposes the use of multiple (several geographical seasons with similar climatology) and multivariable (several variables) data for the prediction of missing data.

Related work

It is of interest, for this research, to evaluate time series imputation in multiple and multivariable data using the algorithms: Expectation Maximization with Bootstrap (EMB), MissForest (a type of Random Forest) and a deep learning model based on Long Short-Term Memory (LSTM).

In the article by Jerez et al. [4], it is concluded that the use of machine learning techniques is the best approach when it comes to imputing data and obtaining significant improvements in terms of accuracy prediction. In the article by Liu et al. [5], results show that multiple data imputation methods outperform other approaches in handling missing data. In the article by Quinteros et al. [6], it’s determined that multiple data imputation can be successful in reconstructing a dataset with better performance when covariates from other seasons are included.

To expand on the EMB algorithm, the following results presented by Chen et al. [7] were used. Here, EMB was used to solve the problems of scarcity of rain registered in the available time series and it was compared against the DA (Data Augmentation) algorithm. With the increase in the scarcity rate from 0% to 60%, in general, the variance in the EMB algorithm was not less than 86.00 and it fitted the observed value better than the DA algorithm. Therefore, the dataset interpolated by the EMB algorithm was much better than the one interpolated by the DA algorithm since it was closer to the observed value [7]. Also, the EMB imputation method can be applied to the imputation of missing data during periods of high flow, periods of normal flow, or periods of low flow. This fact should be considered an important advantage of the EMB algorithm [7].

The other algorithm of interest is Random Forest, used in [2, 8]. [2] show that, in general, Random Forests performed adequately and slightly better compared to linear interpolation and ARIMA. RMSE is used as a metric to assess the effectiveness of data imputation. It is worth mentioning that in this research the main analysis does not focus on the behavior of the Random Forest algorithm. Different algorithms were compared regarding missing gaps in water flow patterns, Random Forest shows an acceptable behavior (close to the average). 

In the research carried out by Cao in [9], most RNN-based methods, except GRU-D, demonstrate significantly better performance on imputation tasks than non-RNN (Non-Recurrent Neural Networks) algorithms. It is emphasized that GRU-D does not impute the missing values explicitly. M-RNN uses an explicit imputation procedure and achieves remarkable imputation results. The BRITS (Bidirectional Recurrent Imputation for Time Series) model significantly outperforms all reference models. The results of the experiments indicate that BRITS demonstrates more accurate results for both imputation and classification/regression than state-of-the-art methods. It is important to clarify that the recurrent layer in the BRITS architecture is based on LSTM as RNN [9].

Experimental design

Data statement

Data not available. For this research, climatological data captured by ICAFE (Instituto del Café de Costa Rica), a non-state public entity, is used, strictly, to evaluate the process of planting and harvesting coffee by said institution.

In this section, it is furtherly described the data available for this research. In summary, we used data on weather stations belonging to the same geographical area. Each weather station has the variables: precipitation, maximum temperature, outdoor temperature, dew point and outdoor humidity. The amount of data available ranges from December 1st, 2013 to April 30th, 2015, giving a total of 12,382 observations (recorded per hour) for each weather station.

Evaluation metrics

The response variables correspond to the metrics that will be used as a comparative value between the algorithms and the model. MAE (Mean Absolute Error), RMSE (Root Mean Squared Error), R2 (Coefficient of determination) and execution time (time taken by the algorithm to perform the imputation of data).

Dataset

The dataset used in this research was provided by the Costa Rican Coffee Institute (ICAFE), which has a series of sensors in different areas around the country where multiple variables of the Costa Rican weather are monitored. However, for various reasons, data has not always been able to be collected effectively.

ICAFE datasets are made up of 32 weather stations or seasons, where each weather station has multiple variables. For the purposes of this study, the variables are technically delimited to outdoor temperature (in Celsius), maximum temperature (in Celsius), outdoor humidity (percentage of relative humidity), dew point (in Celsius) and precipitation (in cubic millimeters).

It is important to clarify that each station has 2 sensors, one outdoors and the other located in a warehouse, so indoor and outdoor humidity may not be correlated due to factors such as air conditioning or fans in the warehouse.

Four datasets were used in this research (seasons 9, 10, 11 & 12), coming from weather stations located in the Los Santos area, so all of them have very similar characteristics to each other (regarding their geographic location and climatic characteristics).

Figure 1 shows the data analysis carried out at the 32 stations provided by ICAFE, the columns represent the year, the rows the weather station number and the blank spaces represent missing days in the time series. When the blank space between the data is small, it can be assessed whether what is missing are hours or days that could be filled in in order to achieve a more complete time series (under criteria explained later). When the blank space is greater than 2 pixels, according to the graph, it can be understood that more than 2 consecutive days of data are missing.

The weather stations are grouped according to the geographical area they belong to (geographical zones are distinguished from each other by different colors). Some of the cells in white can be worked on (filled in), assuming that these are days or hours that don’t usually show very variant weather behaviors and that the edges (previous and after hours) that surround the missing gap in the data exhibit that the weather has not changed significantly during that time. The idea of filling in this data is to convert the blanks to the respective color of the zone, in order to produce a more robust dataset to use in training.

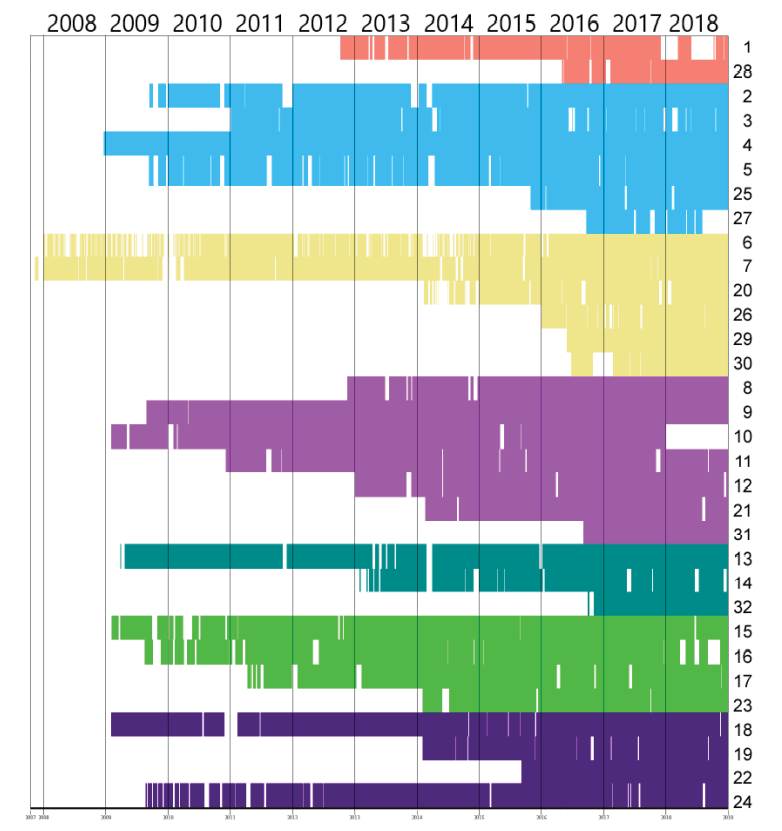
Figure 1. Analysis of the 32 ICAFE weather stations.

Factor selection

All possible factors that influenced the experiments are listed below.

•Datasets: Real data provided by ICAFE was used, data on weather stations belonging to the same geographical area identified by the numbers 9, 10, 11 and 12. Each season has the variables: precipitation, maximum temperature, outdoor temperature, dew point and outdoor humidity. These variables were chosen because they share some correlation between them. The amount of data available for each weather station ranges from December 1st, 2013 to April 30th, 2015, giving a total of 12,382 observations (recorded per hour).

•Train, validation and test sets: The data was divided into 80% for training, 10% for validation and 10% for testing.

•Missing data: Time series datasets with missing data at 1%, 3%, 5%, 10% and 20% rates were generated from the original datasets previously mentioned. This means, for each original dataset (each weather station), another five datasets were generated, each one with a different missing data rate.

Selection of the experimental design

The proposed machine learning model was trained, validated and tested with season 9 and it predicted data for seasons 10, 11 and 12, resulting in 15 experiments. It was compared to another 30 new experiments from the EMB and MissForest results, resulting in a total of 45 experiments in this section.

Development environment

Next, the necessary tools and requirements for the preprocessing, implementation, execution and validation of the experiments are detailed.

•Python programming language: Use of the keras library, missForest library and other libraries: pandas, numpy, random, math, statsmodels, scipy, sklearn, matplotlib, ipython, wandb, tensorflow, kerastuner, keras, math, seaborn.

•R programming language: Use of the Amelia library and Rcpp.

•Operating system and minimum hardware: The tests were executed in Google Colab (Jupyter Notebooks), therefore, the technical specifications of the machine used are, Windows HP Pavilion with an Intel Core i3, 8GB RAM of 2.0 GHZ processor.

Data preprocessing

With the purpose of preprocessing the dataset, many factors had to be analyzed in order to obtain a dataset with similar characteristics between the seasons and their periodicity. The preprocessing process involves carrying out a series of transformations to the content of each weather station in order to reduce the noise present in the time series data and thus make the dataset as uniform as possible.

•From the 32 stations, new weather stations with the 5 variables of interest were generated: outdoor temperature (Temp Out), maximum temperature (Hi Temp), outdoor humidity (Out Hum), dew point (Dew Pt.) and precipitation (Rain).

•For each of the new weather stations, we proceeded to generate stations only with observations every 60 minutes, since it works as an adequate combination in quantity of data and periodicity according to the stations available in the study.

•The presence of the data in the 32 stations is analyzed. Two or more stations from the same geographical area are required and they must share the same time interval of data. This, in order to choose weather stations with similar characteristics (in their geographical location) and that contain an insignificant number of missing values (preferably cells with very small blank spaces), since the data group to be used must be as complete as possible to avoid introducing observations that deviate from the normal behavior of the data, which in turn can introduce noise to algorithms.

•Together with an expert from ICAFE, we proceeded to analyze the set of extracted data: the identification of stations with similar weather conditions (it is determined that the area of Los Santos, represented in purple, meets these characteristics), which datasets contain complete (or almost complete) data, the definition of the data filling criteria according to the number of missing hours (only blank spaces less than 4 hours are filled in) and the season of the year in which said data is missing. All the above was done in order to define the weather stations and intervals in the time series that will be the basis for training the machine learning model.

•We carried out an automatic data filling process through all stations 9, 10, 11 and 12 in the Los Santos area. This process consists of filling in any missing data less than or equal to 4 hours of data in a day. If the range of missing hours is greater, interval files are generated indicating the initial day with its initial time and the final date with its final time, thus identifying when the data could not be filled in since there was a time gap greater than 4 hours.

•The interval files generated for each station were analyzed to verify if it is feasible to manually fill in the data. The number of days in the missing gap were examined: which month of the year it is located, and, through observation of all the variables’ behaviors, it is decided whether to fill in the data with data from previous days and check that the variables share a behavior similar to the days that directly adjoin the missing days.

According to the steps detailed above, it is determined that stations 9, 10, 11 and 12, with dates between December 2013 and April 2015, give us the possibility of having 4 stations with similar geographical conditions and each one with 12,382 observations, one observation per hour every day from December 2013 to April 2015.

Next, it was evaluated if the data follow a normal distribution, by using skewness and kurtosis. Skewness and kurtosis values between -2 and +2 are considered acceptable to demonstrate a normal univariate distribution (George Mallery, 2010). Cabello et al. (2010) and Bryne (2010) argued that the data is considered normal if the skewness is between -2 and +2 and the kurtosis is between -7 and +7 [10].

Unlike the other variables, precipitation has a distribution like the Pareto distribution [11]. Precipitation was the only variable that did not meet the requirement of following a normal distribution and is one of the assumptions required by the EMB algorithm when imputing the data, however, in the results section it will be expanded how EMB performed, with and without precipitation. The algorithm was able to impute missing values even when dealing with precipitation, without significantly raising the error.

Proposed machine learning architecture using LSTM

A couple of variations of LSTM architectures were considered by hyperparameterization with different tools such as Keras Tuner and Wandb. The deep learning architecture developed in this research is based on the architecture proposed by Alhamid in [12]. In his work, Alhamid proposes an architecture based on 2 hidden layers, followed by 2 bidirectional LSTM layers and an additional hidden layer. The input is a sequence of events, and the output is the prediction of the next event in the sequence. 

Based on the study by Sucholutsky [13], some recommendations and guidelines provided in his research are compiled for the present research: the use of the Adam optimizer and the suggestion of including a bidirectional RNN as future work; he uses 5 hidden layers, however, he concludes that additional layers do not improve performance.

The input layer of our model is a Sequential layer, followed by an LSTM layer with 64 units and uses 24 steps in the past (for prediction) and the 5 variables. The next layer is a Bidirectional layer that wraps an LSTM layer with 32 units and a 0.5 dropout. Next, there’s a Gaussian Noise layer to add robustness (mitigate overfitting). 

The next layer is a Repetition Vector with 1 step to the future, this layer works as a bridge between the encoder and decoder. Next, the decoder is defined as a mirror of the first LSTM encoder layer. Then, a Gaussian Dropout layer with a dropout probability of 0.5 is used.

Finally, the output layer is a Time Distributed layer that wraps a Dense layer, which outputs 1 step in the future for the 5 variables and has “relu” as activation function.

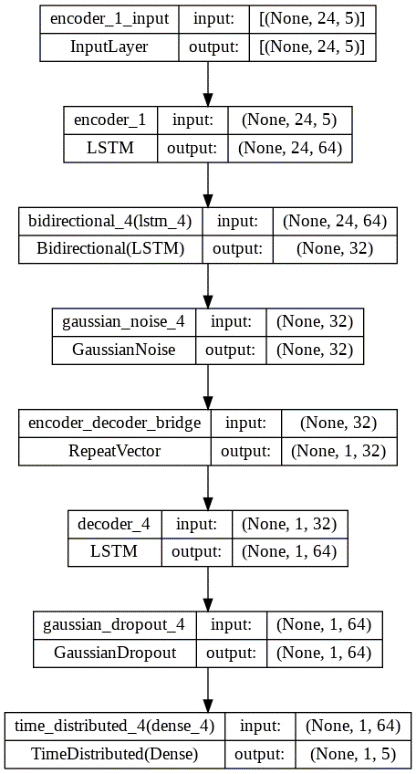
Figure 2. Proposed LSTM architecture.

Hyperparameterization

EMB

The EMB algorithm did not require any hyperparameterization (since trying to parameterize it did not provide improvements to the performance and added execution time), the missing data were imputed with the “default” configuration. The algorithm is represented in its most basic form by not specifying a time column, since this generates more processing time, therefore, the time complexity is not limited by some polynomial (referring to polytime and splinetime parameters from the Amelia library in R).

MissForest

The MissForest algorithm was not hyperparameterized (except for experimental design B, however, the “default” configuration neither other variant in configuration managed to address the problem of filling in consecutive data gaps). Adding more decision trees did not show improvements and the other default parameters applied well for the current case. Within the possibilities presented by the algorithm, the “fit” can be done on a weather station and the “transform” can be done on another weather station, unlike EMB, which can only impute on a weather station without carrying out any prior training or analysis.

LSTM

The LSTM model was hyperparameterized using the random search methodology on the parameters: timesteps, epochs, learning rate, merge mode and loss. The model that seems to minimize (RMSE, MAE) or maximize (R2) the metrics was chosen.

Table 1 shows the variables and values tested during hyperparameterization. To reduce the number of experiments, station 9 and station 10 sets were always used. To choose the best model, the results produced by RMSE, MAE and R2 were considered when predicting data for the 1%, 3%, 5%, 10%, and 20% missing rates.

Table 1. Hyperparameters and values used in the random search of the LSTM model parameters.

Hyperparameter	Tested Values	Selected Value
Batch size	128, 64, 32, 16	32
Activation function	relu, sigmoid	relu
Timesteps	72, 48, 24, 12, 5	24
Epochs	100, 80, 50, 20, 10	100
Learning rate	0.0001	0.0001
Merge mode	sum, mul, concat, ave	concat
Loss	mse	mse

Experiments: Results & Discussion

Experimental Design A

Weather station 9 dataset is used for training, validation and testing the proposed LSTM architecture. Then, the model predicts missing data from weather stations 10, 11 and 12. Missing data is selected at completely random cells (timestamp x variable cell).

Table 2 shows the results obtained for station 10. We evaluated metrics MAE, RMSE, R2 and Execution time for each algorithm (EMB, MissForest and LSTM model) at 1%, 3%, 5% and 10% of missing data. This means, 1% represents imputation on a station 10 dataset in which 1% of its data is missing, and so on with each of the percentages.

LSTM does show a higher error rate compared to MissForest and EMB. As limitations, it is found that EMB can only impute data using the same station (station 10 is used), MissForest can fit with one station and impute another station (fit with station 9 and imputation on station 10; only 80% of station 9 was used for fitting, since for the LSTM model 80% is for training).

The results based on RMSE metric show that MissForest and EMB do much better than the proposed LSTM architecture, indicating greater error when imputing, being MissForest the one with the best metrics overall. However, for 1%, 3%, 5% and 10% of missing data in R2, LSTM architecture competes with good metrics against MissForest and EMB algorithms.

Table 2. Experimental design A. Metrics resulting from data imputation on weather station 10 and training with station 9.

	EMB				MissForest				LSTM model
	MAE	RMSE	R2	Execution time	MAE	RMSE	R2	Execution time	MAE	RMSE	R2	Execution time
1%	0.01	0.11	0.99	1.86 sec	0.001	0.05	0.99	56.00 sec	0.02	0.54	0.99	4.00 sec
3%	0.03	0.32	0.99	2.48 sec	0.01	0.24	0.99	55.00 sec	0.07	0.91	0.98	4.00 sec
5%	0.05	0.42	0.98	1.72 sec	0.02	0.30	0.99	65.00 sec	0.12	1.20	0.97	5.00 sec
10%	0.12	0.88	0.93	2.08 sec	0.05	0.65	0.96	37.00 sec	0.26	1.74	0.91	5.00 sec
20%	0.31	1.70	0.88	2.84 sec	0.17	1.24	0.92	52.00 sec	0.58	2.47	0.82	4.00 sec

Experimental Design B

This variant contemplates the possibility that the missing data is presented sequentially for all the variables, replicating the use case for when the sensor recording the weather data completely loses tracking of the variables for a period of 2 to 5 consecutive days until reaching 1%, 3%, 5%, 10% and 20% of missing data. Among the important findings, it was observed that MissForest completely fails to handle the imputation of consecutive data on all variables. Even though EMB assumes that the missing data is found randomly (missing at random assumption), it still manages to impute the missing data more effectively than the other algorithms in comparison. The proposed LSTM algorithm repeats data from previous windows, since it doesn’t have information from other variables (only from the 24-hour window of past steps) and, therefore, imputation is not good.

Experimental Design C

Considering that recurrent neural networks require a lot of data for training and in the previous experiments the amount of data present per season is relatively little (1 year and 4 months), we proceeded to evaluate other ranges (in years).  Seasons 8 and 9 coincide with data from 2014 to 2018 (doubling the amount of data). The algorithms are re-trained and retested, but with more data. Essentially, this design is like experimental design A, but using more data, and training with season 8 and imputing on season 9. 

Metrics are very similar to the results from experiment A (less than half the data), regardless, there was a small improvement.

Table 3. Experimental design C. Metrics resulting from data imputation on weather station 9 and training with station 8.

	EMB				MissForest				LSTM model
	MAE	RMSE	R2	Execution time	MAE	RMSE	R2	Execution time	MAE	RMSE	R2	Execution time
1%	0.01	0.10	0.99	4.66 sec	0.001	0.07	0.99	144.00 sec	0.02	0.52	0.99	12.00 sec
3%	0.02	0.21	0.99	4.9 sec	0.004	0.15	0.99	142.00 sec	0.06	0.79	0.98	12.00 sec
5%	0.03	0.30	0.98	5.00 sec	0.01	0.20	0.99	114.00 sec	0.10	1.03	0.96	12.00 sec
10%	0.07	0.55	0.96	5.17 sec	0.03	0.38	0.98	198.00 sec	0.22	1.43	0.92	23.00 sec
20%	0.22	1.21	0.89	5.43 sec	0.11	0.88	0.93	111.00 sec	0.50	2.04	0.79	23.00 sec

Experimental Design D

In this experimental design, a new dataset was created by using each variable from the season that was best correlated with the variable in question. A new mixed dataset that contains the 5 variables taken from the best correlated stations is created. To illustrate the above, if the precipitation variable from season 9 is to be imputed, one looks for which of the nearby stations 10, 11 or 12 has the best correlation regarding the precipitation variable and extracts that entire column of data. This goes the same way for the remaining variables. 

We train the model with the new mixed dataset and impute on the original dataset with missing gaps. This experiment was not performed on EMB nor MissForest since it focuses on the training phase. EMB and MissForest results from experiment A were compared against the results of experiment D of the proposed LSTM. When comparing experiments A and D it was concluded that, despite the fact that the stations are imputed by variable in correlation with other stations in the same geographical area, when combining the station variables, the metrics do not improve and this could be explained due to the loss of the real behavior of the data and trend between the variables.

Experimental Design E

In this experimental design test, it is intended to simulate the scenarios of real cases to which ICAFE is exposed to when there is data loss (lack of battery in the solar sensor, missing at random hours due to short circuit, missing in ranges less than 24 hours due to desynchronization with the datalogger, among others). It is important to clarify that the missing data developed in this section were generated manually, simulating the possible scenarios of missing data in ICAFE (missing only a few or all variables for multiple consecutive or non-consecutive hours; mixing these cases for a weather station until reaching the missing data rate). 

Next, in Table 4 the metrics obtained in this design are shown and it can be deduced that the LSTM model performs better than the EMB and MissForest imputation algorithms.

Table 4. Experimental design E. Metrics resulting from data imputation on weather station 10 and training with station 9.

	EMB				MissForest				LSTM model
	MAE	RMSE	R2	Execution time	MAE	RMSE	R2	Execution time	MAE	RMSE	R2	Execution time
1%	0.05	0.78	0.98	2.18 sec	0.03	0.43	0.99	76.00 sec	0.02	0.40	0.99	5.00 sec
3%	0.14	1.32	0.94	2.35 sec	0.09	1.00	0.97	40.00 sec	0.08	0.93	0.98	5.00 sec
5%	0.23	1.68	0.92	2.18 sec	0.15	1.32	0.95	40.00 sec	0.13	1.25	0.96	5.00 sec

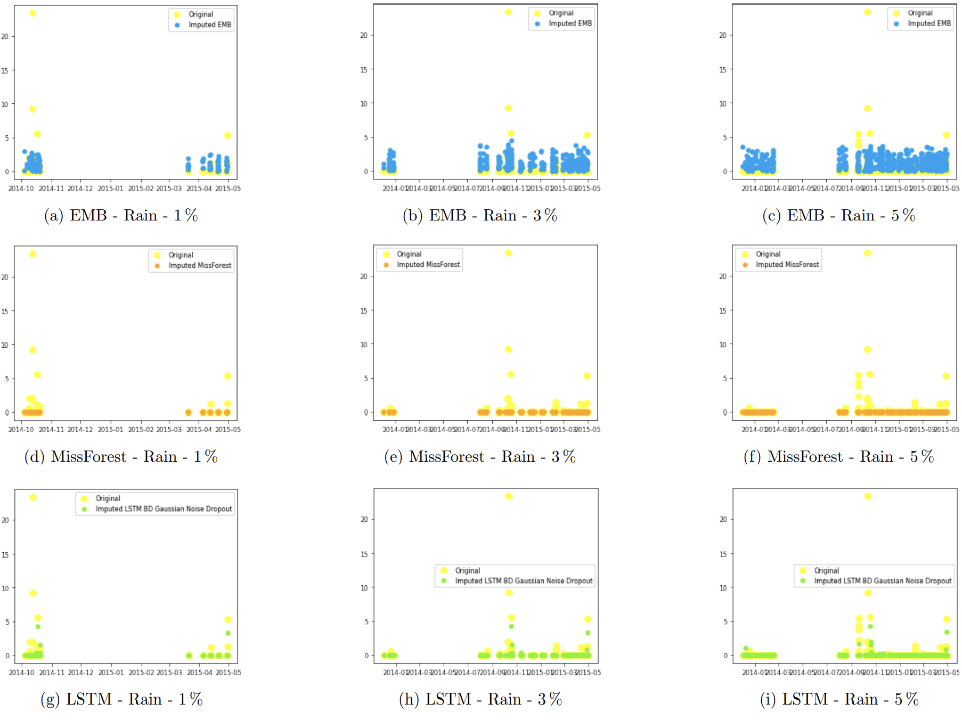
Figure 3. Experiment E, imputation for variable Rain with missing data at 1%, 3% and 5% rate.

If we look at the algorithm’s predictions per variable (the original value is in yellow and the predicted value by the algorithm is in the other color), we can conclude that:

•Regarding the Rain variable, Figure 3 shows that EMB keeps imputing data, almost at random, in a range. MissForest does not try to predict the values or get close to an approximate and LSTM tries to predict the missing data in a more intelligent way by trying to follow the behavioral pattern of the data.

•Results for dew point, maximum temperature,outdoor humidity and outdoor temperature show that EMB is the algorithm that best deals with imputation of the missing data, MissForest does not try to predict the values or come close to an approximate and LSTM tries to predict the missing data the same by following the behavior patterns, however it has a lower limit that does not allow it to impute below itself, still, LSTM demonstrates it looks for trends and seasonalities to predict missing values.

•We raise the question if evaluating the same LSTM model but without an activation function will have an effect on the lower limit indicated in the previous point.

•Additionally, for each of the variables, it is evaluated an acceptance range (using a scale of minimums and maximums provided by ICAFE per variable and, furthermore, evaluating the website https://www.tiempo3.com/north-america/costa-rica?page=today and determining what could be the ranges in which a variable can vary from one hour to another). In this way it is established that:

»Rain: In the morning it changes little, about 0.33 mm every 3 hours, and at night the change between hours can go up to 6 mm. Minimum and maximum acceptable values: 0 – 25 mm. Accepted difference respecting the original value vs. the imputed value: 1 mm.

»Temp Out (outside temperature): There’s abrupt changes when the sun comes in and out; can be up to 4 degrees. Minimum and maximum acceptable values: 10 – 40 degrees Celsius. Accepted difference respecting the original value vs. the imputed value: 2 degrees.

»Hi Temp (maximum temperature): Must be greater than or equal to Temp Out. Minimum and maximum acceptable values: 10 – 40 degrees Celsius. Accepted difference respecting the original value vs. the imputed value: 2 degrees.

»Out Hum (outside humidity): It can vary by 3% and when the sun rises, can change up to 5%. Minimum and maximum acceptable values: 40 – 100 %. Accepted difference respecting the original value vs. the imputed value: 3%.

»Dew Pt. (dew point): May vary by 2 degrees and cannot be greater than the outside temperature. Minimum and maximum acceptable values: 10 – 40 degrees Celsius. Accepted difference respecting the original value vs. the imputed value: 2 degrees.

To calculate if a value is accepted, it is only evaluated if the imputed value falls within the acceptance range established by variable or if it meets the restrictions of being greater than another variable (in the case of dew point and outside humidity), in any other case said imputation is rejected. The results obtained from evaluating the algorithms with acceptance ranges can be seen in Table 5; for each season, it was calculated the percentage accepted values represented in the total count.

It is perceptible that given the acceptance ranges described, the acceptance percentages achieved by LSTM demonstrate better performance against the imputations made by the other algorithms.

Table 5. Experimental Design E. Metrics obtained by evaluating EMB, MissForest and LSTM with acceptance ranges.

	EMB				MissForest				LSTM model
	S9	S10	S11	S12	S9	S10	S11	S12	S9	S10	S11	S12
1% 3% 5%	0.40 0.37 0.35	0.34 0.33 0.31	0.37 0.37 0.35	0.30 0.30 0.28	0.48 0.60 0.58	0.51 0.50 0.50	0.45 0.53 0.51	0.43 0.43 0.46	0.71 0.66 0.67	0.51 0.52 0.54	0.66 0.63 0.62	0.43 0.44 0.46

Concluding remarks

The MissForest algorithm has the best results in experiments A, C and D, based solely on metrics. However, MissForest fails to impute missing data consecutively for all columns simultaneously: in the experimental design E, it is shown that MissForest, despite having acceptable general metrics, gets stuck at mean imputation (which is the first step on the algorithm). At the level of visualization per variable, the graphs demonstrate MissForest isn’t trying to impute missing data at all. MissForest needs multivariate data, but in experimental design B and E, data was missing consecutively for all variables. The EMB algorithm seems to be the best option for experimental design B, but metrics were not competitive compared to the ones obtained in other experimental designs.

The LSTM model in experimental case C shows that the greater the amount of data for training, the model shows small improvements in the imputation metrics. However, there is little availability of data between stations in the same area that allow us to verify if with a substantial number of years of data, the algorithm improves significantly. Similarly, the results obtained in experimental design D did not represent a significant improvement. Even though its metrics compete with the results from experimental design A, it is not recommended to use this approach, especially when dealing with time series data, given that when you create a new dataset that does not represent the original behavior of data, you can introduce noise and lose seasonality and trends.

When an analysis is performed per variable on experimental design E, with acceptance ranges or rejection criteria for each imputation made by the proposed LSTM, EMB and MissForest algorithms, it is concluded that the imputations made by LSTM have better acceptance rates compared to the other algorithms. Even though, visually, EMB seems to follow the data patterns to an extent, predictions fail to fall into the acceptance ranges in its majority. LSTM did a better job at understanding the actual behavioral model of the data, since predictions fulfill the acceptance criteria for the most part. However, LSTM predictions have a lower limit that does not allow it to impute below itself.

References

[1] Y. Zhang, P. J. Thorburn, W. Xiang and P. Fitch, “SSIM—A Deep Learning Approach for Recovering Missing Time Series Sensor Data” in IEEE Internet of Things Journal, vol. 6, no. 4, pp. 6618-6628, 2019, doi: 10.1109/JIOT.2019.2909038.

[2] N. Bokde, M. W. Beck, F. Martínez-Alvarez and K. Kulat, “A novel imputation methodology for time series based on pattern sequence forecasting” in Pattern Recognition Letters, vol. 116, no. 7, pp. 88-96, 2018, doi: 10.1016/j.patrec.2018.09.020.

[3] N. Donges. “A Guide to Recurrent Neural Networks: Understanding RNN and LSTM Networks” Built In, 2021, builtin.com/data-science/recurrent-neural-networks-and-lstm. Accessed 18 Apr. 2022.

[4] J. M. Jerez, I. Molina, P. J. García-Laencina, E. Alba, N. Ribelles, M. Martín and L. Franco, “Missing data imputation using statistical and machine learning methods in a real breast cancer problem” in Artificial Intelligence in Medicine, vol. 50, no. 2, pp. 105-115, 2010, doi: 10.1016/j.artmed.2010.05.002.

[5] T. Liu, H. Wei, and K. Zhang, “Wind power prediction with missing data using Gaussian process regression and multiple imputation” in Applied Soft Computing, vol. 71, pp. 905-916, 2018, doi: 10.1016/j.asoc.2018.07.027.

[6] M. E. Quinteros, S. Lu, C. Blazquez, J. P. Cárdenas-R, X. Ossa, J.-M. Delgado-Saborit, R. M. Harrison, and P. Ruiz-Rudolph, “Use of data imputation tools to reconstruct incomplete air quality datasets: A case-study in Temuco, Chile” in Atmospheric Environment, vol. 200, pp. 40-49, 2019, doi: 10.1016/j.atmosenv.2018.11.053.

[7] L. Chen, J. Xu, G. Wang, and Z. Shen, “Comparison of the multiple imputation approaches for imputing rainfall data series and their applications to watershed models” in Journal of Hydrology, vol. 572, pp. 449-460, 2019, doi: 10.1016/j.jhydrol.2019.03.025.

[8] S. Moritz, A. Sardá, T. Bartz-Beielstein, M. Zaefferer, and J. Stork, “Comparison of different Methods for Univariate Time Series Imputation in R”, 2015, doi: 10.48550/arXiv.1510.03924.

[9] W. Cao, D. Wang, J. Li, H. Zhou, L. Li, and Y. Li, “BRITS: Bidirectional Recurrent Imputation for Time Series”, in Advances in Neural Information Processing Systems 31 (NeurIPS 2018), 2018, doi: 10.48550/arXiv.1805.10572.

[10] F. Oppong and S. Yao, “Assessing Univariate and Multivariate Normality, A Guide For Non-Statisticians”, in Mathematical Theory and Modeling, vol. 6, no. 2, pp. 26-33, 2016.

[11] Y. Kim, H. Kim, G. Lee, and K.-H. Min, “A Modified Hybrid Gamma and Generalized Pareto Distribution for Precipitation Data”, in Asia-Pacific Journal of Atmospheric Sciences, vol. 55, no. 4, pp. 609-616, 2019, doi: 10.1007/s13143-019-00114-z.

[12] A. Mohammed, “LSTM and Bidirectional LSTM for Regression - Towards Data Science”, Medium, 2022, towardsdatascience.com/lstm-and-bidirectional-lstm-for-regression-4fddf910c655. Accessed 10 Feb. 2022.

[13] I. Sucholutsky, A. Narayan, M. Schonlau, and S. Fischmeister, “Deep Learning for System Trace Restoration”, 2019 International Joint Conference on Neural Networks (IJCNN) (2019): 1-8, doi: 10.48550/arXiv.1904.05411.

[14] J. Honaker, G. King, and M. Blackwell, “Amelia II: A Program for Missing Data”, in Journal of Statistical Software, vol. 45, no. 7, pp. 1-47, 2011, doi: 10.18637/jss.v045.i07.

[15] J. J. Miró, V. Caselles, and M. J. Estrela, “Multiple imputation of rainfall missing data in the Iberian Mediterranean context”, in Atmospheric Research, vol. 197, pp. 313-330, 2017, doi: 10.1016/j.atmosres.2017.07.016.

[16] A. V. Desherevskii, I. Zhuravlev, N. Nikolsky, and Y. Sidorin, “Problems in Analyzing Time Series with Gaps and Their Solution with the WinABD Software Package” in Izvestiya, Atmospheric and Oceanic Physics, vol. 53, no. 7, pp. 659-678, 2018, doi: 10.1134/S0001433817070027.

[17] A. Andiojaya and H. Demirhan, “A bagging algorithm for the imputation of missing values in time series”, in Expert Systems With Applications, vol. 129, no. 3, pp. 10-26, 2019, doi: 10.1016/j.eswa.2019.03.044.

[18] L. Campozano, E. Sanchez, A. Avilés, and E. Samaniego, “Evaluation of infilling methods for time series of daily precipitation and temperature: The case of the Ecuadorian Andes”, in Maskana¸ vol. 5, no. 1, pp. 99-115, 2014, doi: 10.18537/mskn.05.01.07.

[19] M. B. Richman, T. B. Trafalis, and I. Adrianto, “Multiple imputation through machine learning algorithms”, 87th AMS Annual Meeting, 2007.

[20] C. Zhai, “A Note on the Expectation-Maximization (EM) Algorithm”, 2004.

[21] J. Honaker, and G. King, “What to do About Missing Values in Time Series Cross-Section Data”, in American Journal of Political Science, vol. 54, no. 2, pp. 561-581, 2010, doi: 10.1111/j.1540-5907.2010.00447.x.

[22] T. Khampuengson and W. Wang, “Novel Methods for Imputing Missing Values in Water Level Monitoring Data”, in Water Resources Management, vol. 37, no. 2, pp. 851-878, 2023, doi: 10.1007/s11269-022-03408-6

---

1. 1 Instituto Tecnológico de Costa Rica, Cartago, Costa Rica.
   cristina.arias.munoz@gmail.com

1. 2 Instituto Tecnológico de Costa Rica, Cartago, Costa Rica.
   susanacob254@gmail.com

1. 3 Instituto Tecnológico de Costa Rica, Cartago, Costa Rica.
   lcalvo@itcr.ac.cr