Modelación computacional de la corrosión del refuerzo metálico de un concreto carbonatado

Computational modelling of steel rebars corrosion in carbonated concrete

Bruno Chinè-Polito1, Ronald Jiménez-Salas2, Rommel Cuevas-Kauffmann3

Fecha de recepción: 1 de febrero, 2023
Fecha de aprobación: 28 de mayo, 2023

Chinè-Polito, B; Jiménez-Salas, R; Cuevas-Kauffmann,R. Modelación computacional de la corrosión del refuerzo metálico de un concreto carbonatado. Tecnología en Marcha. Vol. 37, No 1. Enero-Marzo, 2024. Pág. 51-64.

https://doi.org/10.18845/tm.v37i1.6532

Palabras claves

Concreto; carbonatación; corrosión del refuerzo metálico; ensayos de resistencia a polarización; modelación computacional.

Resumen

En el sector civil de la construcción, el concreto y el refuerzo metálico representan aun los materiales de mayor importancia, aunque sean muy vulnerables por los agentes atmosféricos, como en el caso de su degradación por corrosión. En este artículo se presenta un trabajo de modelación computacional de la corrosión del refuerzo metálico de un concreto carbonatado, basado en datos experimentales de un proceso de carbonatación acelerada y sucesiva corrosión de las varillas metálicas. El modelo ha sido completado incorporando los datos cinéticos experimentales de las reacciones electroquímicas de los electrodos que están en relación con el avance del frente de carbonatación. A partir de los valores experimentales del potencial de corrosión, densidad de corriente de corrosión, pendientes anódicas y catódicas de la curva de Tafel, se estiman las corrientes de intercambio anódicas y catódicas y finalmente se simula la corrosión de las varillas metálicas de muestras de concreto reforzado.

Keywords

Concrete; carbonation; metallic rebars corrosion; polarization resistance tests; computational modelling.

Abstract

In the construction sector, the concrete and the steel bars represent still the key components, although they are very vulnerable by the atmospheric agents, as in the case of their degradation caused by corrosion. In this work we present a computational modelling work of reinforced bars corrosion in a carbonated concrete, based on experimental data obtained form an accelerated carbonation process and successive corrosion of metallic bars. The model has been completed incorporating experimental kinetic data of the electrochemical electrode reactions linked to the carbonation front progress. Starting from the experimental values of corrosion potential, corrosion current density, and anodic and cathodic slopes of the Tafel curve, the values of anodic and cathodic exchange currents have been computed and then used to simulate the corrosion of the reinforcing bars in concrete samples.

Introducción

Aunque el concreto y el refuerzo metálico son muy vulnerables por los agentes atmosféricos, representan los materiales de mayor uso para la realización de obras civiles. Debido al aumento de CO2 en la atmosfera por el cambio climático, se hace necesario evaluar el impacto de la corrosión sobre las estructuras civiles [1,2] por razones de seguridad y por los altos costos asociados a su reparación o sustitución. En Costa Rica el problema es relativamente importante por la insuficiencia de métodos de monitoreo de las estructuras existentes y la deficiente política preventiva en términos de mantenimiento. El concreto es fundamentalmente un material cerámico poroso [3], con una estructura expuesta a procesos de corrosión atmosférica originados por la carbonatación. Este mecanismo ataca el metal del concreto reforzado, el cual presenta una capa oxidada en su superficie, estable termodinámicamente y que lo protege de la corrosión (pasivación). Sin embargo, el dióxido de carbono CO2 difundiendo en el concreto modifica las condiciones alcalinas de la solución dentro de los poros (reacciones de neutralización) y la superficie metálica pierde la capa de protección (depasivación) [4]. Una serie de artículos fundamentales sobre el proceso de carbonatación se deben al autor Papadakis [5,6,7,8,9]. Los efectos de la carbonatación sobre propiedades mecánicas y durabilidad del concreto son estudiados mediante pruebas aceleradas [10], evaluando el rol de CO2 y humedad relativa [11] y con un análisis estadístico para estimar la velocidad del fenómeno [12]. Se investigan las propiedades mecánicas de los refuerzos metálicos deteriorados por la corrosión [13] y se evalúan las velocidades de corrosión máxima y mínima de refuerzos metálicos [14]. Numerosos trabajos investigan el proceso de corrosión del refuerzo metálico, uno de los autores pioneros es Bazant [15]. Un estudio computacional de la corrosión por cloruros se desarrolla en [16], la dependencia del mecanismo de reacción catódica en función del grado de saturación de agua es objeto del trabajo de Huet el al. [17] y en [18] se analiza la cinética de la corrosión de varillas metálicas por carbonatación del concreto. También se desarrolla el acoplamiento del transporte de oxígeno con un modelo de corrosión micro-celda [19] y una evaluación de corrosión por cloruros en morteros de cemento [20]. Además, se simula la corrosión del refuerzo en un concreto carbonatado por CO2 atmosférico [21] y más recientemente se investiga la corrosión del refuerzo en un proceso de carbonatación de un concreto binario alcalino-activado [22]. También han sido publicados numerosos trabajos computacionales, para estudiar la corrosión en muestras de aleaciones de aluminio usando Comsol Multiphysics [23] y para los casos de corrosión inducida por iones cloruros [24], entre otros. Se representa numéricamente el mecanismo electroquímico de re-alcalinización [25], el transporte de los agentes corrosivos y el sistema de reacciones electroquímicas [26]. Otros autores proponen una relación inversa entre densidad de corriente y potencial [27] o un algoritmo no-linear para la modelación de la corrosión del acero [28]. Por otro lado, se usan reconstrucciones microestructurales del concreto con tomografía de rayos X computarizada [29] y se acoplan fenómenos de carbonatación y corrosión [30]. En [31] se estudia la corrosión bajo ataque salino y en [32] se implementa un modelo 3D para las fallas en refuerzos metálicos. También se brindan modelos para la propagación de la corrosión del acero [33], la carbonatación de materiales cementicos introduciendo una porosidad aleatoria [34] y el análisis de estructuras fisuradas por corrosión [35]. Se incorporan métodos computacionales de phase field parar describir la superficie de un ánodo metálico [36] y se desarrollan estudios de las reacciones de corrosión [37]. Boukhlef et al. [38] sugieren un modelo computacional con soluciones analíticas y numéricas obtenidas por elementos finitos, otros analizan teóricamente la pendiente de la curva de Tafel anódica y el potencial eléctrico [39] o estudian el sistema de corrosión localizada [40]. Finalmente, varios trabajos recientes aplican métodos computacionales para la modelación de fenómenos de carbonatación y corrosivos, entre otros [41,42,43].

Modelación computacional del proceso de corrosión

Hipótesis del modelo

El proceso corrosivo puede romper la capa de pasivación que protege el acero, cuando la alcalinidad de la solución acuosa (electrolito) de los poros del concreto decrece por la carbonatación [15,4,44]. Consiste en la disolución de hierro en el agua de los poros, pues el hierro se oxida y los iones 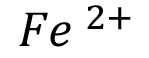pasan en solución, según la reacción anódica:

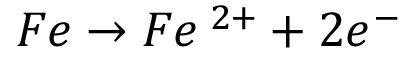(ánodo) (1)

siendo 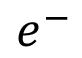es el electrón. Las regiones de la superficie del acero cercanas a las áreas anódicas se desempeñan como áreas catódicas y los 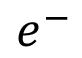se mueven hacia allí, creando una corriente eléctrica desde regiones catódicas hacia anódicas. Simultáneamente, el oxígeno atmosférico difunde en el concreto hacia la superficie metálica y, en los sitios catódicos a contacto con la solución acuosa, reacciona con los electrones de la reacción 1. Se origina la siguiente reacción de reducción con la formación de iones hidroxilo OH --:

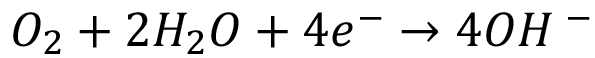(catodo) (2)

La corriente eléctrica pasa a través del electrolito, desde la superficie anódica hacia el área

catódica y es originada por el transporte en sentido contrario de las cargas negativas OH --. Por otro lado, los iones OH -- que llegan a la región anódica neutralizan eléctricamente los iones 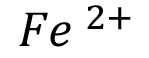disueltos y forman una solución de hidróxido ferroso Fe(OH)2 :

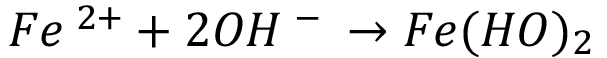(ánodo) (3)

La reacción global de celda, sumando las reacciones 1, 2 y 3 es por lo tanto:

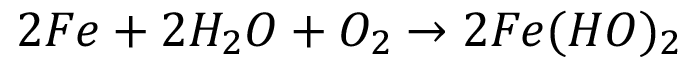(celda) (4)

Las ecuaciones. 2,3,4 evidencian que el O2 es fundamental para el fenómeno corrosivo del refuerzo metálico. Se asume que en los poros el agua es suficiente para el desarrollo de las reacciones anteriores, influenciando el proceso de corrosión mediante dos mecanismos [15]: a) el grado de saturación del agua afecta la resistividad eléctrica del concreto; b) del mismo grado de saturación depende el coeficiente de difusión de los gases O2 y CO2.

Consecuentemente, se fijan las siguientes hipótesis para el modelo computacional:

a.el concreto es un medio poroso no completamente saturado con agua, donde el fenómeno de carbonatación modifica el estado de pasivación del refuerzo metálico;

b.el proceso de óxido-reducción se modela mediante oxidación de Fe y reducción del O2 en la superficie total del refuerzo metálico (carbonatación tipo micro-celda);

c.el O2 atmosférico circunstante el concreto difunde en la fase gaseosa de los poros, hacia los refuerzos metálicos;

d.las reacciones electroquímicas de corrosión son controladas por la concentración del O2 en proximidad del refuerzo metálico, en presencia de suficiente agua;

e.se desprecia el material oxidado del refuerzo y los cambios volumétricos de este;

f.el fenómeno de corrosión se modela en condiciones estacionarias.

Para el modelo, se brindan en las secciones sucesivas la geometría y propiedades físicas de las muestras de concreto reforzado, los parámetros del proceso de carbonatación desarrollado experimentalmente en cámara acelerada y los valores de las mediciones electroquímicas [45].

Desarrollo del modelo con el software Comsol Multiphysics

La figura 1 esquematiza la geometría de una muestra de concreto reforzado [45], preparada con cemento hidráulico Holcim MP/A-28 y con los materiales y relativas cantidades del cuadro 1. La relación final agua/cemento en el concreto es de 0.57 con una tasa agregados/cemento de 4.17, aproximadamente. En la parte superior de figura 1 se muestra una vista vertical de la muestra y una sección metálica expuesta de 50 mm de largo para una barra de 130 mm de altura, indicando además los recubrimientos de silicona superior e inferior que aíslan estas regiones metálicas. La parte inferior de la figura brinda una sección horizontal con la posición, desde la superficie lateral, de las 5 varillas de acero de 10 mm de diámetro. En la misma figura se indica el sistema de coordenadas cartesianas rectangulares, x,y,z del modelo computacional desarrollado en Comsol Multiphysics v5.4 [46] en condiciones estacionarias, isotérmicas a 25 °C y presión de 1 atm. Se estudia el caso de la corrosión de la muestra carbonatada por 33 días, excluyendo la varilla central en los cómputos, pues representa solo un electrodo de referencia. Para el O2 gaseoso, se fija la concentración de 8.58 mol/m3 en los bordes, que corresponde a un volumen parcial de oxígeno de 21% en la cámara de carbonatación. Con excepción de las superficies metálicas expuestas, donde se desarrollan las reacciones de reducción, todas las restantes paredes se consideran impermeables al O2. Usando una correlación de Papadakis et al. [7], al medio poroso se asigna una porosidad de 0.32 y una saturación de agua igual a 0.27, para una relación agua/cemento de 0.57 y humedad relativa de 65% en la cámara de carbonatación. Se asume que el O2 se desplaza en la fase gaseosa de los poros, se estima su coeficiente de trasporte efectivo en 2.5x10-8 m2/s en función de la porosidad y de la humedad relativa [7] y se fija también igual a 8.58 mol/m3 la concentración inicial de O2 en el dominio. Para la corrosión de las cuatro varillas de refuerzo, se modela el concreto como medio electrolítico con conductividad eléctrica efectiva de 0.005 S/m [31]. Con excepción de las regiones expuestas del metal, se impone que todas las restantes superficies son aisladas eléctricamente, en el electrolito y en el electrodo. Se desprecia el cálculo de la corriente eléctrica en el interior del metal, siendo la conductividad de este mucho mayor que la del electrolito. Finalmente, la malla computacional tridimensional desarrollada en Comsol Multiphysics para aplicar el método de elementos finitos numérico, se compone de 2.0x106 elementos tetraédricos y de 1.2x105 elementos triangulares, generando un modelo con alrededor de 8.55x105 grados de libertad.

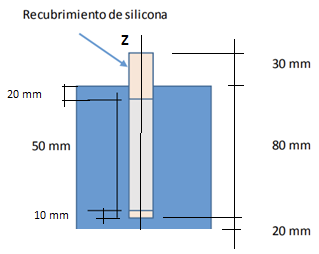
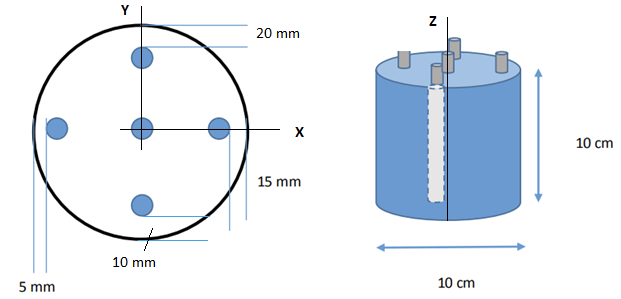
Figura 1. Esquema de la muestra de concreto reforzado con las barras de acero, dimensiones y orientación del sistema de coordenadas cartesianas rectangulares, x, y, z.

Cuadro 1. Dosificaciones de los materiales para la elaboración de la mezcla de concreto.

Material	Condición	Peso (kg)	Dosificación
Cemento Hidráulico (MP/A-28)	Seco	381.97	1
Arena	Húmeda	687.31	1.80
Piedra	Húmeda	907.12	2.37
Agua	Sin aditivo	197.45	0.52

Nota: la dosificación de agua/cemento es de 0.52; el valor final de la relación agua/cemento en el concreto es de 0.57, según los valores de humedad de la arena y piedra medidos en laboratorio.

Cinética de las reacciones electroquímicas

Parte fundamental del modelo computacional es la definición de la cinética de las reacciones electroquímicas en las superficies de los electrodos. Inicialmente, con el indicador fenolftaleína se estiman las profundidades carbonatada del concreto, que para la muestra carbonatada 33 días en la cámara acelerada, a una concentración de CO2 del 25% y humedad relativa de 65%, es de es aproximadamente 18 ± 1 mm desde la superficie exterior. Para la misma muestra, el cuadro 2 reporta los valores experimentales del ensayo de polarización para las cuatro varillas colocadas a diferentes profundidades. A medida que la carbonatación es más intensa, cerca de las varillas que se encuentran a 5 mm y 10 mm desde la superficie externa, los potenciales de corrosión son más negativos y la intensidad de corriente es mayor. Para las varillas a 15 mm y 20 mm de profundidad los resultados son muy similares entre sí y evidencian que el metal mantiene aún un cierto grado de pasividad. Con los valores de potencial de corrosión Ecorr, densidad de corriente de corrosión icorr, pendientes anódicas ba y catódicas bc de la curva de Tafel, se pueden estimar las corrientes de intercambio anódicas y catódicas [44] de las varillas metálicas. La corriente de intercambio iO para la oxidación del Fe se obtiene extrapolando la curva de Tafel anódica hacia el valor del potencial de equilibrio del Fe (- 0.631 V vs electrodo de Ag/AgCl en solución 1M de KCl a 25 °C). Para la reducción del O2, la corriente de intercambio se determina extrapolando la curva de Tafel catódica hacia el valor del potencial de equilibrio del O2 (1.007 V vs electrodo de Ag/AgCl en solución 1M de KCl a 25 °C). En el cuadro se brindan los valores de iO, de oxidación y reducción, para las cuatro barras de acero. Los valores de iO , ba y bc se usan en el modelo para describir la cinética electroquímica de las interfaces metal/concreto.

Cuadro 2. Corrientes de intercambio de oxidación del hierro y de reducción del oxígeno, para las varillas de la muestra con 33 días de carbonatación, mediante ensayos de polarización (el potencial de corrosión Ecorr se mide con respecto a un electrodo de Ag/AgCl saturado, a 25°C).

Muestra	Ecorr (V)	icorr (A/cm2)	ba (V/dec)	bc (V/dec)	iO de oxidación de Fe (A/cm2)	iO de reducción de O2 (A/cm2)
33-5 mm	-0,6507	9,1468E-06	0,92964	-0,91109	0.1017 E-04	0.1308 E-06
33-10mm	-0,6051	7,5005E-06	0,88559	-0,82915	0.0744 E-04	0.0800 E-06
33-15mm	-0,5685	4,0430E-06	0,64922	-0,60148	0.0351 E-04	0.0089 E-06
33-20mm	-0,5239	6,4684E-06	1,0871	-0,8971	0.0541 E-04	0.1199 E-06

Resultados y análisis

La figura 2 muestra el potencial eléctrico y las líneas de densidad de corriente del electrolito para la corrosión del refuerzo metálico. Cuando fluye corriente eléctrica, el concreto (electrolito) en las regiones donde las reacciones anódicas son más intensas, presenta un potencial eléctrico más positivo que el concreto de las regiones donde estas son menos intensas. Por lo tanto, cuando el Fe se oxida, los iones Fe++ se disuelven en el concreto cercano, mientras que los 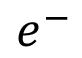de la reacción se desplazan en el metal y, en correspondencia de la región catódica, son disponibles para la reducción del O2. En figura 2 la densidad de corriente eléctrica en el electrolito es directamente proporcional a la diferencia de potencial eléctrico. Esta cantidad está dada por la diferencia entre el potencial del electrolito cercano a las regiones anódicas más intensas, menos el potencial del electrolito de aquella región donde el fenómeno corrosivo es menos intenso. La diferencia de potencial eléctrico permite el cálculo de la densidad de corriente, a través de la ley de Ohm. La figura 3 muestra la distribución de O2 en un plano horizontal que secciona el cilindro en correspondencia de la mitad de su altura (z = 50 mm), intersecando las regiones metálicas de hierro. Se nota la disminución de O2 en las áreas próxima a las varillas metálicas, en particular en las regiones que miran hacia el centro, debido al consumo de O2 en las reacciones de reducción y que representa un sumidero modelado por la ley de Faraday.

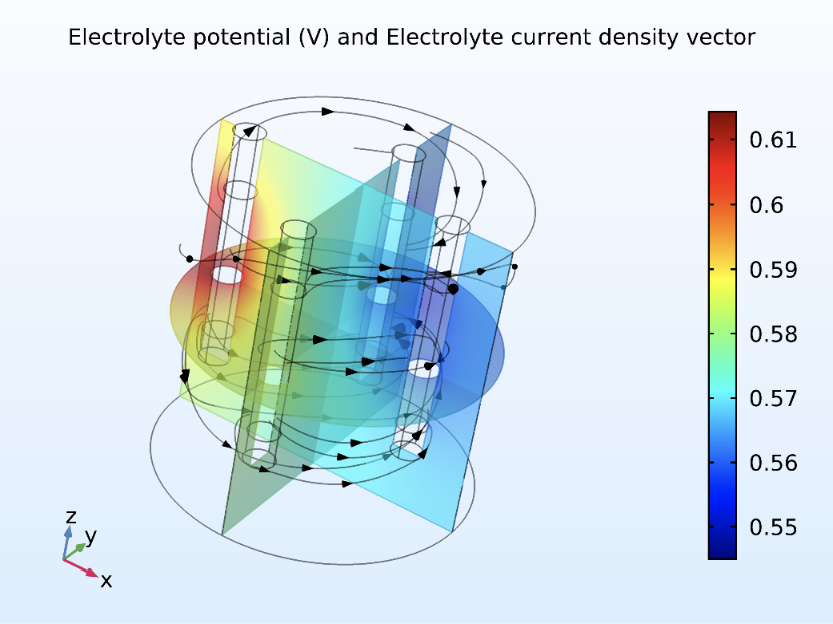
Figura 2. Valores de potencial eléctrico y líneas de densidad de corriente en el electrolito, para el proceso de corrosión del refuerzo metálico.

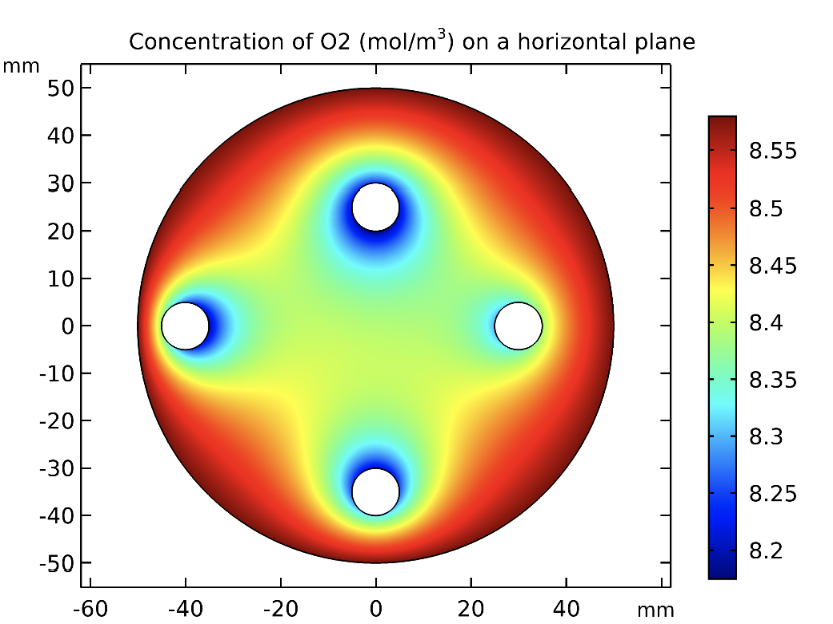
Figura 3. Concentración de oxígeno sobre un plano horizontal del concreto reforzado (z = 50 mm).

La figura 4 muestra las líneas de la densidad de corriente en el volumen del electrolito. Se nota que en proximidad de la barra posicionada a 5 mm de la superficie exterior en el lado negativo del eje x, la corriente eléctrica es más intensa y la concentración de O2 es baja, por las reacciones de reducción que lo consumen. Para la barra ubicada a 20 mm de la superficie externa en lado positivo del eje y, la concentración de O2 es aún más baja, pues este electrodo es más distante de la periferia, donde la concentración es alta. Para el modelo, que implementa la cinética electroquímica de las ecuaciones de Tafel y desprecia el cálculo de la corriente eléctrica en el interior del metal, se define nulo el potencial 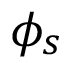de la fase metálica y se calcula el sobre-potencial 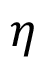con la expresión 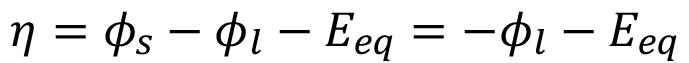, donde 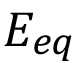es el potencial de equilibrio y 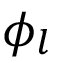el potencial del electrolito. Del cuadro 2 se obtienen las distintas corrientes de intercambio y pendientes de Tafel, para representar la reducción del O2 y la oxidación del Fe para las cuatro varillas. La figura 5 muestra las líneas de densidad en el electrolito y el potencial eléctrico de los electrodos versus el de referencia. Las líneas de densidad de corriente del electrolito nacen en las regiones donde la oxidación del Fe es más intensa, es decir en las varillas más externas, en la zona carbonatada. El mecanismo se evidencia también en la figura 6 que traza el potencial del electrolito con la densidad de corriente en un plano horizontal a z = 50 mm. Se puede observar que las áreas con potencial mayor se ubican cerca de las varillas oxidadas más externas.

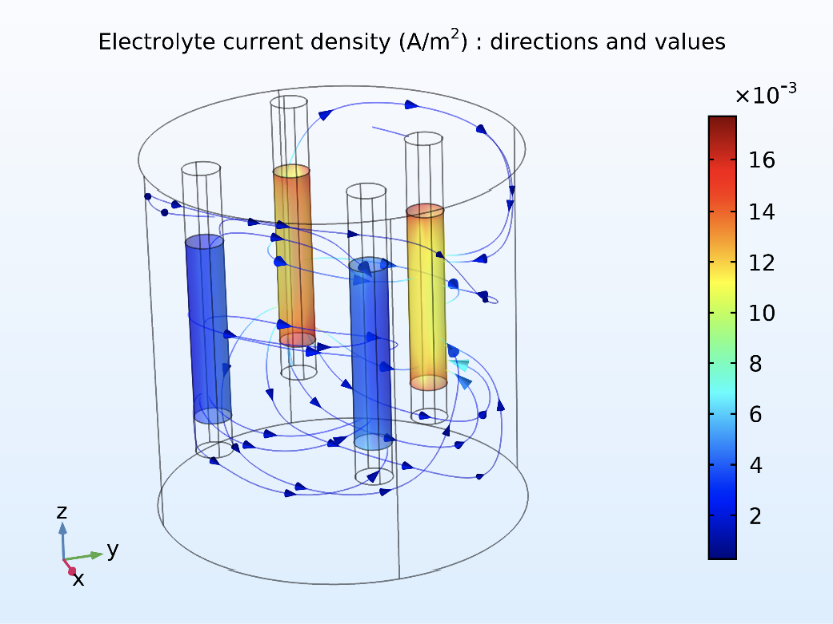
Figura 4. Líneas de densidad de corriente en el electrolito y valores en las fronteras de las varillas, para la corrosión metálica del refuerzo.

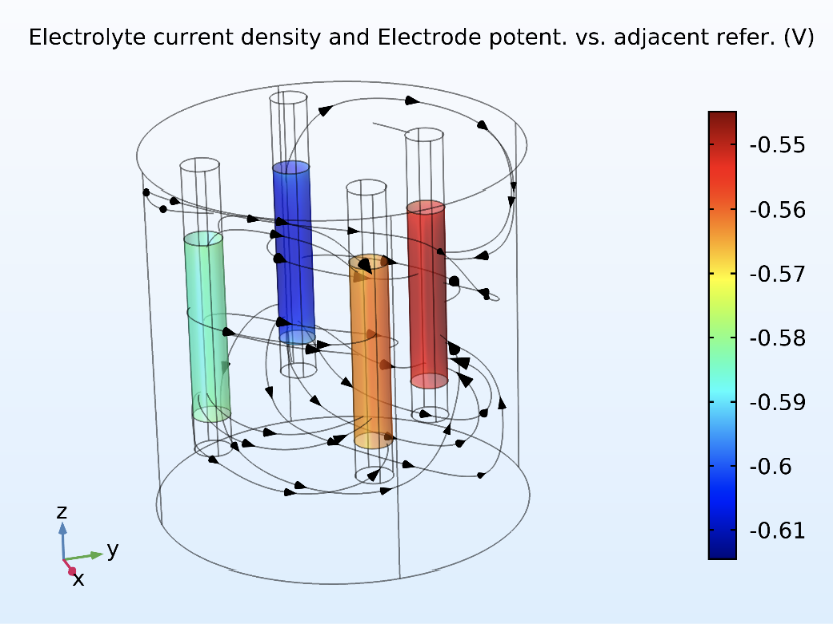
Figura 5. Líneas de densidad de corriente en el electrolito y potencial eléctrico de los electrodos vs referencia en el proceso de corrosión del refuerzo metálico.

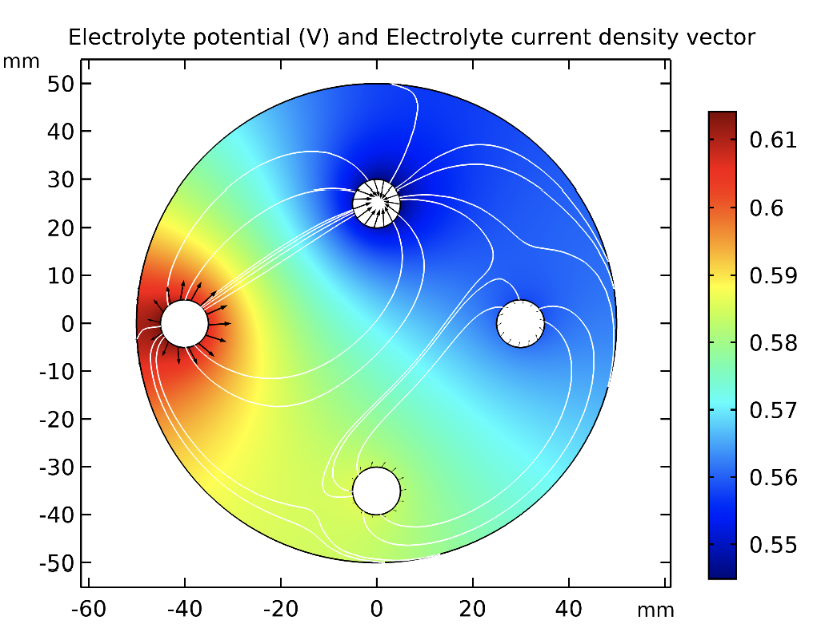
Figura 6. Valores de potencial eléctrico y líneas de densidad de corriente en el electrolito, sobre un plano horizontal del concreto reforzado (z = 50 mm).

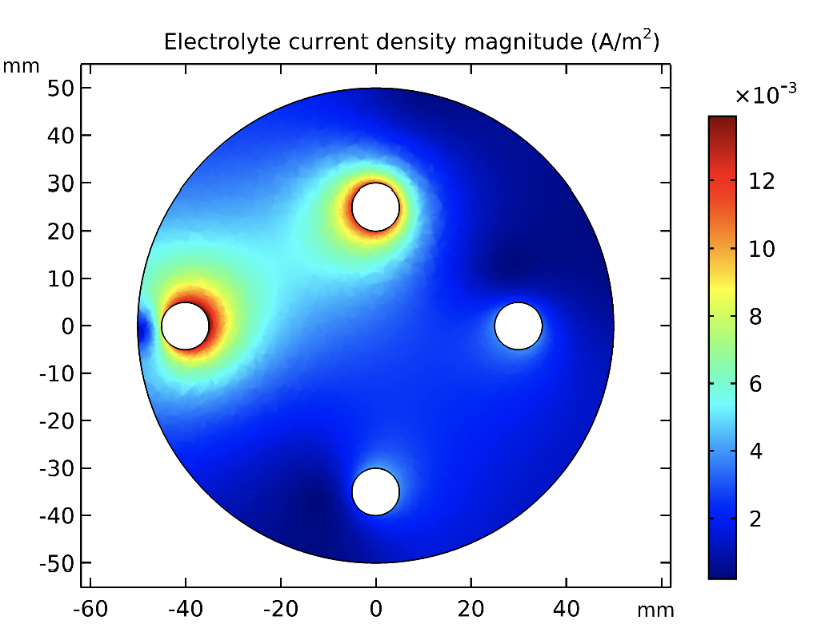
Figura 7. Valores de la magnitud de la densidad de corriente en el electrolito, sobre un plano horizontal del concreto reforzado (z = 50 mm).

En la figura 7 se brinda la magnitud de la densidad de corriente en el electrolito, en plano horizontal z = 50 mm. En el gráfico de figura 8 se muestra la densidad de corriente de la oxidación (o de corrosión) del Fe, para todas las varillas metálicas con su posición desde la superficie exterior. Las interfaces donde se calcula la corriente son líneas verticales opuestas al centro del espécimen de concreto y mirando hacia el externo. Por otro lado, la figura 9 reporta los resultados de la reducción del O2 en las mismas interfaces. Se observa que la corriente de oxidación del Fe para la varilla a 5 mm de la superficie exterior es mayor que las de las restantes, pues se encuentra en una región carbonatada, donde los mecanismos electro-químicos de corrosión son más favorables.

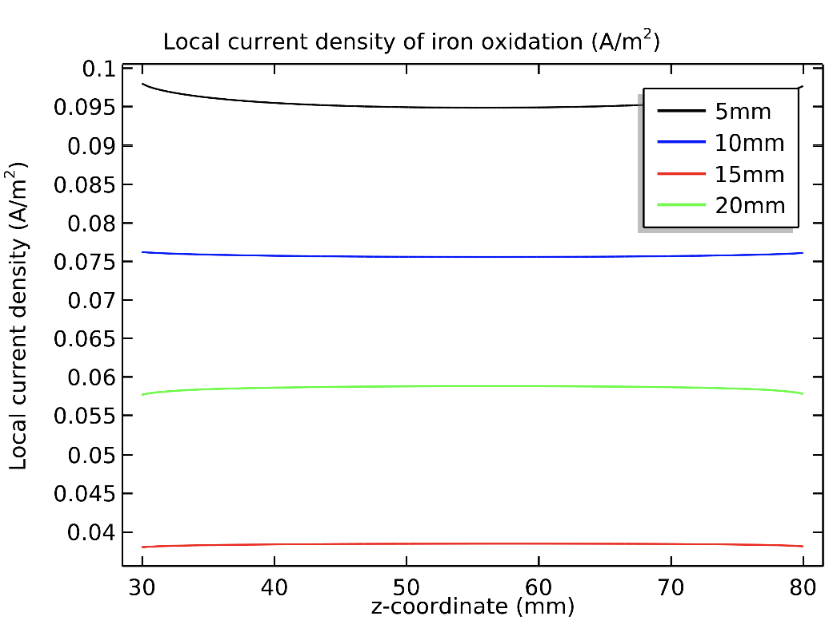
Figura 8. Densidad de corriente de oxidación del hierro en la interfaz superficie metálica-concreto, para las 4 varillas posicionadas a diferentes distancias de la superficie exterior.

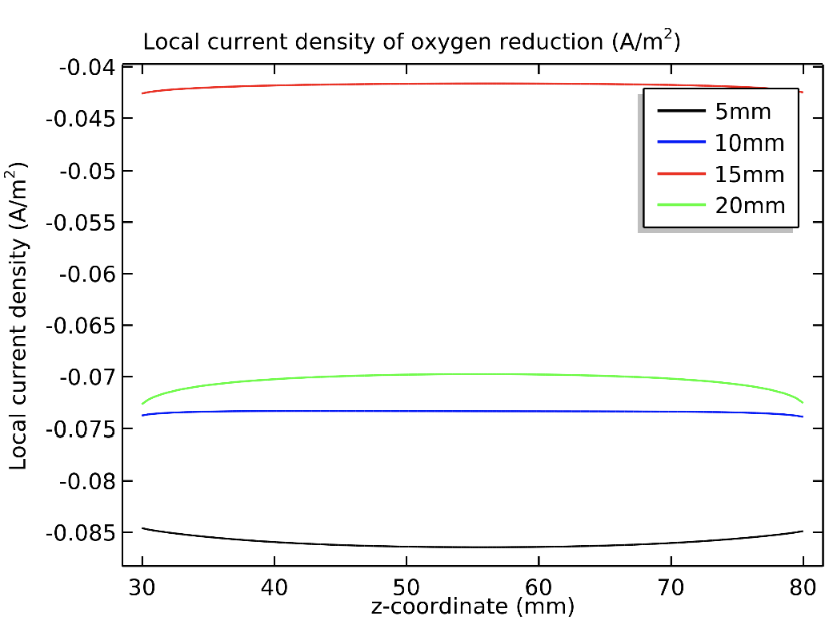
Figura 9. Densidad de corriente de reducción del oxígeno en la interfaz superficie metálica-concreto, para las 4 varillas posicionadas a diferentes distancias de la superficie exterior.

Según el cuadro 2, las varillas, con excepción del refuerzo puesto a 20 mm del exterior, se caracterizan por una corriente de corrosión que decrece con la profundidad de estas. Los resultados de la figura 9 muestran un comportamiento similar para la corriente de reducción del O2, es decir la densidad de corriente de reducción es mayor para la varilla más externa, donde además el O2 difunde más rápidamente desde el ambiente. Los valores de las densidades de corrientes anódicas, para las dos varillas más externas, a 5 y 10 mm de profundidad, son superiores a las de las correspondientes corrientes catódicas. Estos resultados se analizan con del potencial de interfaz, es decir con la sobretensión anódica 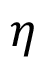. Cuando en algunas regiones el potencial 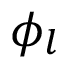es menor, allí 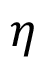es mayor y así la corriente de corrosión dada por la ecuación de oxidación de Tafel. Para el caso del O2, la velocidad de reducción aumenta con su concentración en el electrolito y, por la ecuación catódica de Tafel, con los valores más negativos de 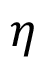correspondientes a las interfaces colocadas en regiones donde el potencial 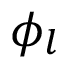es mayor.

Conclusiones

El modelo ha sido desarrollado incorporando datos cinéticos experimentales de las reacciones electroquímicas de los electrodos, que están en relación con el mecanismo de carbonatación en una cámara de carbonatación acelerada. En particular en el software se han usado datos del ensayo de polarización para las cuatro varillas colocadas a diferentes profundidades en el espécimen de concreto reforzado. El análisis de los resultados obtenidos ha indicado que a medida que la carbonatación es más intensa, como ocurre con las varillas más cercanas a la superficie externa, los potenciales de corrosión son más negativos y la intensidad de corriente presenta valores más grandes. Finalmente, a partir de los valores de potencial de corrosión, densidad de corriente de corrosión, pendientes anódicas y catódicas de la curva de Tafel, se han estimado las corrientes de intercambio anódicas y catódicas y simulado la corrosión de las varillas metálicas de las muestras de concreto reforzado.

Agradecimientos

Los autores agradecen la Vicerrectoría de Investigación y Extensión del ITCR para el apoyo al proyecto 5401-1411-3001 “COrrosión del concreto reforzado y DEgradación de sus propiedades MECánicas (CODE_MEC3): Estudio experimental y modelación de la degradación de propiedades mecánicas del concreto reforzado por causa de la corrosión”.

Referencias

[1] ASCE, “Report card for America’s infrastructure”, American Society of Civil Engineers, Reston, VA, 2013.

[2] X. Wang, M. Nguyen, M. Stewart, M. Syme and A. Leitch, “Analysis of climate change impacts on the deterioration of concrete infrastructure”. Part 1: Mechanisms, Practices, Modeling and Simulations - A Review, CSIRO, Canberra, 2010.

[3] W. Hayden, W.G. Moffatt and J. Wulff, “The structure and properties of materials”, Vol. III Mechanical Behavior, John Wiley and Sons, New York, 1965.

[4] Tuutti K., “Corrosion of steel in concrete”, Swedish Cement and Concrete Institute RIT-Stockholm, 1982.

[5] V.G. Papadakis, C.G. Vayenas and M.N. Fardis, “A reaction engineering approach to the problem of concrete carbonation”, American Inst. of Chemical Engineers, 35, N.10, 1639-1650, 1989.

[6] V.G. Papadakis, C.G. Vayenas and M.N. Fardis, “Experimental investigation and mathematical modeling of the concrete carbonation problem”, Chemical Engineering Science, 46, N.5/6, 1333-1338, 1991.

[7] V.G. Papadakis, C.G Vayenas and M.N. Fardis, “Physical and chemical characteristics affecting the durability of concrete”, ACI Materials Journal, 88, N.2, 186-196, 1991.

[8] V.G. Papadakis, M.N. Fardis and C.G. Vayenas, “Hydration and carbonation of pozzolanic cement”, ACI Materials Journal, 89, N.2, 119-130, 1992.

[9] V.G. Papadakis, M.N. Fardis and C.G. Vayenas, “Effect of composition, environmental factors and cement-lime mortar coating on concrete carbonation”, Materials and Structures, 25, 293-304, 1992.

[10] J.M. Chi, R. Huang and C.C. Yang, “Effects of carbonation on mechanical properties and durability of concrete using accelerated testing method”, Journal of marine science and technology, 10, N.1, 14-20, 2002.

[11] N. Zhiguon and Y. Ri, “Experimental investigation of concrete carbonation under different conditions”, Study of Civil Engineering and Architecture (SCEA), 2, N.4, 114-117, 2013.

[12] T.P. Hills, F. Gordon, N.H. Florin and P.S. Fennell, “Statistical analysis of the carbonation rate of concrete”, Cement and Concrete Research, 72, 98-107, 2015.

[13] S. Imperatore, Z. Rinaldi and C. Drago, “Degradation relationships for the mechanical properties of corroded steel bars”, Construction and Building Materials, 148, 219-230, 2017.

[14] Jaśniok M. and Jaśniok T., Evaluation of maximum and minimum corrosion rate of steel rebars in concrete structures, based on laboratory measurements on drilled cores, Procedia Engineering, 193, 486-493, 2017.

[15] Z.P. Bazant, “Physical model for steel corrosion in concrete sea structures”, Journal of the structural division-Proceedings of the ASCE, 105, n. ST6, 1137-1153, June 1979.

[16] T. Maruya, K. Hsu, H. Takeda and S. Tangtermsirikul, “Numerical modeling of steel corrosion in concrete structures due to chloride ion, oxygen and water movement”, Journal of advanced concrete technology, 1, N.2, 147-160, 2003.

[17] B. Huet, V. L’Hostis, G. Santarini, D. Feron and H. Idrissi, “Steel corrosion in concrete: deterministic modeling of cathodic reaction as a function of water saturation degree”, Corrosion Science, 49, 1918-1932, 2007.

[18] P. Dangla and W. Wridi, “Rebar corrosion in carbonated concrete exposed to variable humidity conditions. Interpretation of Tuutti’s curve”, Corrosion Science, 51, 1747-1756, 2009.

[19] R.R. Hussain and T. Ishida, “Development of numerical model for FEM computation of oxygen transport through porous media coupled with micro-cell corrosion model of steel in concrete structure”, Computers and Structures, 88, 639-647, 2010.

[20] M.I. Prieto, A. Cobo, A. Rodriguez and V.Calderón, “Corrosion behavior of reinforcement bars embedded in mortar specimens containing ladle furnace slag in partial substitution of aggregate and cement”, Construction and Building Materials, 38, 188-194, 2013.

[21] T.T.H. Nguyen, B. Bary and T. de Larrard, “Coupled carbonation-rust formation-damage modeling and simulation of steel corrosion in 3D mesoscale reinforced concrete”, Cement and Concrete Research, 74, 95-107, 2015.

[22] R.A. Robayo-Salazar, A.M. Aguirre-Guerrero and R. Mejia de Gutierrez, “Carbonation-induced corrosion of alkali-activated binary concrete based on natural volcanic pozzolan”, Construction and Building Materials, 232, 117189, 2020.

[23] N. Murer, N. Missert and R. Buchheit, “Towards the modeling of microgalvanic corrosion in aluminum alloys: the choice of boundary conditions”, Proceedings of the Comsol Users Conference, Boston (USA), 2008.

[24] C.Y. Kim and J.K Kim, “Numerical analysis of localized steel corrosion in concrete”, Construction and Building Materials, 22, 1129-1136, 2018.

[25] M. Jaśniok and A. Zybura, “Modeling the carbonated concrete realkanilization”, Journal of civil engineering and management, 15, N.2, 159-168, 2009.

[26] P. Ghods, K. Karadakis, O.B. Isgor and G. McRae, “Modeling the chloride-induced corrosion initiation of steel rebar in concrete”, Proceedings of the Comsol Conference 2009 Boston, Boston, Ma, 2009.

[27] L.T.N. Dao, V.T.N. Dao, S.H. Kim and K.Y. Ann “Modeling steel corrosion in concrete structures- Part 1: A new inverse relation between current density and potential for the cathodic reaction”, International Journal of Electrochemical Science, 5, 302-313, 2010.

[28] L.T.N. Dao, V.T.N. Dao, S.H. Kim and K.Y. Ann, “Modeling steel corrosion in concrete structures- Part 2: A unified adaptive finite element method for simulation of steel corrosion”, International Journal of Electrochemical Science, 5, 314-326, 2010.

[29] Y. Lu, E. Garboczi, D. Bentz and J. Davis, “Modeling the chloride transport in cracked concrete: a 3D image-based microstructure simulation”, Proceedings of the Comsol Conference 2012 Boston, Boston, Ma, 2012.

[30] M.G. Sohail, “Corrosion of steel in concrete: Development of an accelerated test by carbonation and galvanic coupling”, PhD thesis, Université de Toulouse, 2013.

[31] C. Cao, “3D simulation of localized steel corrosion in chloride contaminated reinforced concrete”, Construction and Building Materials, 72, 434-443, 2014.

[32] I. Fernandez, J.M. Bairán and A.R. Marí, “3D FEM model development from 3D optical measurement technique applied to corroded steel bars”, Construction and Building Materials, 124, 519-532, 2016.

[33] A. Michel, M. Otieno, H. Stang and M.R. Geiker, “Propagation of steel corrosion in concrete: Experimental and numerical investigations”, Cement and Concrete Composites, 70, 171-182, 2016.

[34] M. Yu, H. Bao, J. Ye and Y. Chi, “The effect of random porosity field on supercritical carbonation of cement-based materials”, Construction and Building Materials, 146, 144-155, 2017.

[35] J. Zhang, X. Ling and Z. Guan, “Finite element modeling of concrete cover crack propagation due to non-uniform corrosion of reinforcement”, Construction and Building Materials, 132, 487-499, 2017.

[36] W. Mai and S. Soghrati, “ New phase field model for simulating galvanic and pitting corrosion processes”, Electrochimica Acta, 260, 290-304, 2018.

[37] F. Babaghayou, B. Zegnini and T. Seghier, “Numerical study and remediation of AC interference corrosion on neighboring pipelines”, Journal of Engineering Science and Technology, 13, N.7, 2047-2064, 2018.

[38] D. Boukhlef, D. Boughrara and H. Mohellebi, “Simulation of border deformation in corrosion system by coupling analytical solution and finite element method”, Journal of Materials and Engineering Structures, 5, 267-277, 2018.

[39] J. Xia, T. Li, J. Fang and W. Jin, “Numerical simulation of steel corrosion in chloride contaminated concrete”, Construction and Building Materials, 228, 116745, 2019.

[40] C. Liu and R.G. Kelly, “A review of the application of finite element method (FEM) to localized corrosion modeling”, Corrosion Journal Org., 75, Issue 11, 1285-1299, 2019.

[41] N. Seigneur, E. Kangni-Foli, V. Lagneau, A. Dauzeres, S. Poyet, P. Le Bescop, E. L’Hopital and J.B. d’Espinose de Lacaillerie, “Predicting the atmospheric carbonation of cementitious materials using fully coupled two-phase reactive transport modelling”, Cement and Concrete Research, 130, 105966, 2020. https://doi.org/10.1016/j.cemconres.2019.105966

[42] P. Liu, Z. Yu and Y. Chen, “Carbonation depth model and carbonated acceleration rate of concrete under different environment”, Cement and Concrete Composites, 114, 103736, 2020. https://doi.org/10.1016/j.cemconcomp.2020.103736

[43] Y. Yu, W. Gao, A. Castel, A. Liu, Y. Feng, X. Chen and A. Mukherjee, “Modelling steel corrosion under concrete non-uniformity and structural defects”, Cement and Concrete Research, 135, 106109, 2020. https://doi.org/10.1016/j.cemconres.2020.106109

[44] D.A. Jones, “Principles and prevention of corrosion”, 2nd Ed., Macmillian Publishing Company, New York, 1992.

[45] B. Chiné, R. Jimenez and R. Cuevas, “Corrosión del concreto reforzado y DEgradación de sus propiedades MECánicas (CODE_MEC2): Etapa 2 Estudio experimental y modelación computacional de la carbonatación y corrosión del concreto reforzado”, código 1490020, Informe Final, Dirección de Proyectos VIE, ITCR, 2021.

[46] Comsol AB, Corrosion Module, User’s Guide, Version 5.4, 2018.

---