Accelerating machine learning at the edge with approximate computing on FPGAs

Acelerando aprendizaje de máquina en el Edge con computación aproximada en FPGAs

Luis Gerardo León-Vega1, Eduardo Salazar- Villalobos2, Jorge Castro-Godínez3

León-Vega, L.G.; Salazar-Villalobos, E.; Castro-Godínez, J. Accelerating machine learning at the edge with approximate computing on FPGAs. Tecnología en Marcha. Vol. 35, special issue. IEEE International Conference on Bioinspired Processing. December, 2022. Pág. 39-45.

https://doi.org/10.18845/tm.v35i9.6491

Keywords

Approximate computing; edge computing; machine learning; neural networks; linear algebra.

Abstract

Performing inference of complex machine learning (ML) algorithms at the edge is becoming important to unlink the system functionality from the cloud. However, the ML models increase complexity faster than the available hardware resources. This research aims to accelerate machine learning by offloading the computation to low-end FPGAs and using approximate computing techniques to optimise resource usage, taking advantage of the inaccurate nature of machine learning models. In this paper, we propose a generic matrix multiply-add processing element design, parameterised in datatype, matrix size, and data width. We evaluate the resource consumption and error behaviour while varying the matrix size and the data width given a fixed-point data type. We determine that the error scales with the matrix size, but it can be compensated by increasing the data width, posing a trade-off between data width and matrix size with respect to the error.

Palabras clave

Computación aproximada; computación periférica; aprendizaje por computador; redes neuronales; álgebra lineal

Resumen

La inferencia en algoritmos complejos de aprendizaje automático (ML, por sus siglas en inglés) en edge computing está tomando importancia para desvincular la funcionalidad de un sistema de la nube. Sin embargo, los modelos de ML incrementan en complejidad más rápido que los recursos de hardware disponibles. Esta investigación tiene como objetivo acelerar el aprendizaje por automático al delegar el cálculo computacional a FPGAs de baja gama y usar computación aproximada para optimizar el uso de los recursos aprovechando la naturaleza inexacta de los modelos de aprendizaje automático. En este artículo, proponemos un diseño de un elemento de procesamiento genérico de multiplicación-suma de matrices, parametrizado en el tipo de dato, tamaño de la matriz y ancho del dato. Evaluamos el comportamiento del consumo de recursos y del error mientras variamos el tamaño de la matriz y el ancho del dato dato un tipo de datos de punto fijo. Determinamos que el error escala con el tamaño de la matriz pero que puede ser compensado al incrementar el ancho del dato, representando un compromiso entre el ancho del dato y el tamaño de la matriz con respecto al error.

Introduction

Deep neural network (DNN) models constantly increase in complexity over time, while edge computing systems tend to be steady in their capabilities [1]. Power consumption is a common concern when moving inference to the edge, adding complexity to dealing with the trade-off between resources and inference time. One possibility to add more control over this trade-off is to use Field Programmable Gate Arrays (FPGA), which are devices capable of reconfiguring their logic and implementing custom hardware designs. This implies exploring the synthesis of inference algorithms described with Hardware Description Languages (HDL) or using High-Level Synthesis (HLS), tools capable of converting C/C++ untimed code to Register Transfer Level (RTL) [2,3]. There are also pre-built alternatives to leverage inference to FPGAs using vendor IP cores, such as Vitis AI and OpenVINO [4,5]. However, most alternatives focus on mid-end to high-end FPGAs, leaving aside the low-end solutions that exhibit less power consumption.

One downside of the pre-built alternatives is that they limit the optimisation opportunities beyond pruning and fixed-point representation. This research aims to address the use of FPGAs to accelerate machine learning operations rather than represent the whole model in hardware, precisely placing the accelerators required for the model execution, improving hardware utilisation, and achieving better energy consumption. The key contribution of this research is the proposal of a framework for creating custom architectures according to the model requirements, in particular, tuned in arbitrary numerical representation, number of processing elements (PE), and quantisation techniques.

Background and Related-Work

According to the state-of-the-art, there are implementations for accelerating matrix-matrix multiplications and convolutions at the industry level. Intel and NVIDIA propose AMX and Tensor cores, respectively, which accelerate matrix fused multiply-add (FMA) [6,7]: D = AB + C integer arithmetic. Convolutions have been optimised through mathematical manipulation. For instance, the Winograd algorithm reduces the number of multiplications involved in the convolution by using a domain transformation [8]. It presents multiple advantages, such as memory footprint and better performance than the spatial convolution, achieving more than 3x in speedup [8].

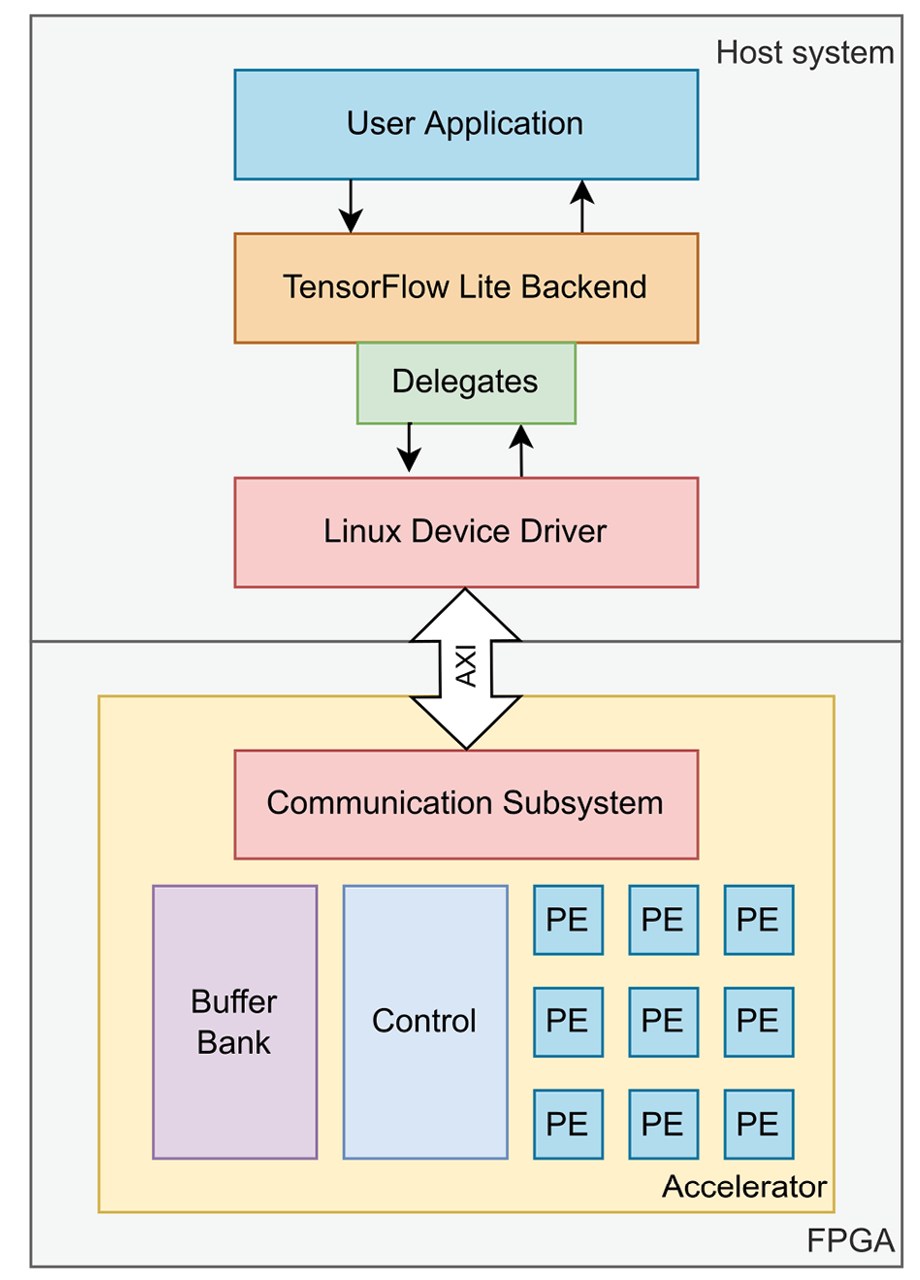
Figure 1. Structure of the research proposal.

Our proposal is presented in Figure 1. It considers the implementation of 1) a set of generic accelerators implemented in standard C++, synthesised using Vivado HLS, and parameterised in datatype, the number of bits, arithmetic operands and number of PEs. 2) A device driver to communicate the accelerators to Linux as the host Operating System and sample implementations using Tensorflow for benchmarking. These implementations are part of a framework for accelerating inference in low-end FPGAs.

The research analyses common mathematical operations performed during model inference, mainly matrix-matrix multiplications, convolutions and non-linear activations. It leads to having a baseline for the accelerators library, which is parameterised to make the designs more flexible than the typical implementations offered in CPUs, GPUs and TPUs, allowing the designer to explore optimisation opportunities. After the first set of implementations in HLS, the PEs will be analysed to model their behaviour when tuning the numerical precision and varying the operand sizes, observing their impact on resource utilisation, numerical errors and energy consumption. It will help users create and evaluate accelerator candidates according to the complexity of the ML model and their design constraints.

For this work, we will focus on the first stage of our framework (the set of accelerators), particularly with a fixed-width matrix fused multiply-add (FMA) PE, parameterised in datatype, data width, and matrix size. In this case, the FMA operator implementation keeps the data width in the output, involving a scaling factor that depends on the matrix dimensions to mitigate the overflow:

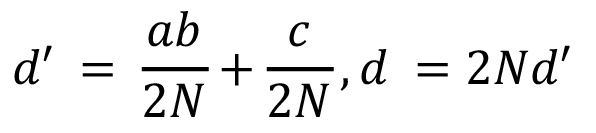(1)

where a, b, and c are the input operands, N is the number of rows considering a square matrix, and d is the output.

Methodology

We start the implementation of the matrix FMA by using standard C++ to define the algorithm itself. After having a correct implementation using floating-point numbers, we start by parameterising the implementation at the data type, matrix size, and the number of bits level. It will lead to inaccuracies in the results that must be evaluated before applying the implementation to an actual application. In this case, we evaluate the errors by using a normalised mean error and its standard deviation 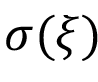, computed as

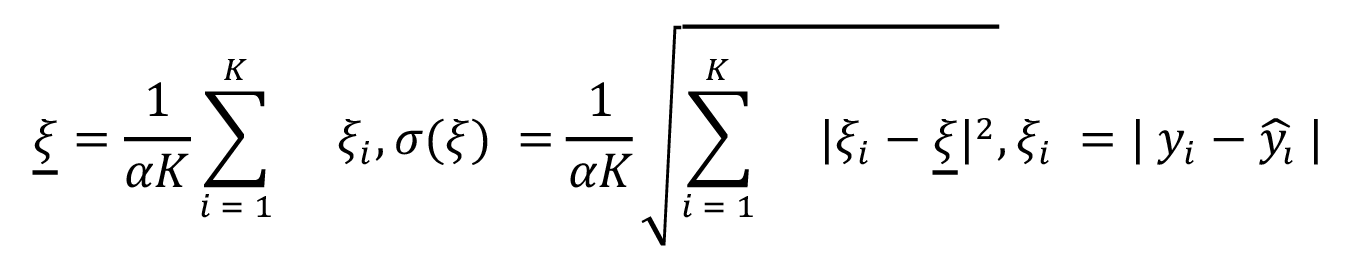(2)

where K is the number of elements of the matrix evaluated (including 10 iterations with different seeds), yi is the i-th floating-point result (matrix entries), 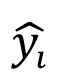is the measured value in a custom data type and a number of bits, and α is the normalisation factor (set to 2 given the numerical range from ] –1,1 [ ).

After evaluating the numerical impact, we proceed with the iterative design optimisation, adding pipelining, registers, and concurrency to the implementation. These optimisations are added through Vivado HLS directive files. In this case, we will present our Pareto’s optimal solution.

Results

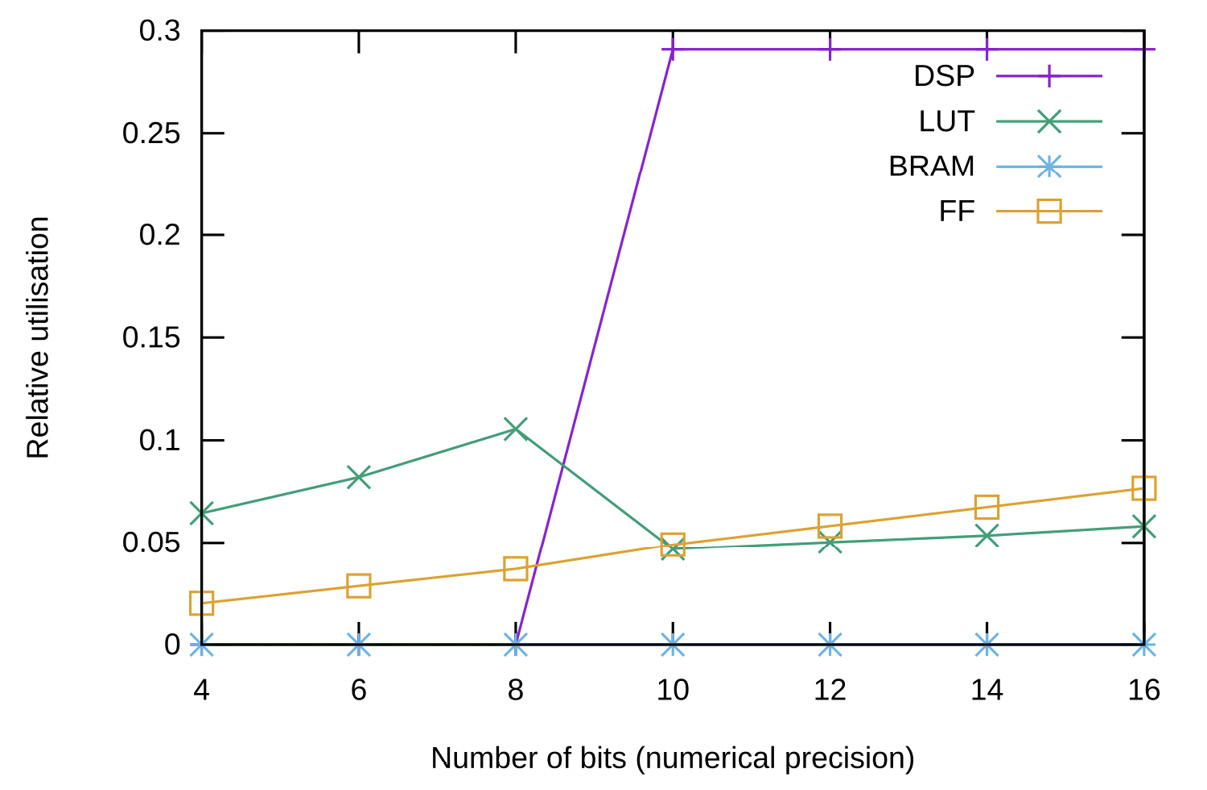
Figure 2. Resource consumption of the current best FMA processing element for 8x8 matrices. The resources analysed are Digital Signal Processors (DSPs), Look-Up Tables (LUTs), Block Random Access Memories (BRAMs), and Flip-Flops (FFs).

Figure 2 presents the results of our current FMA implementation (see [9]). It scales linearly with respect to the data width concerning the FFs used in the design. It has a discontinuity in the LUTs, switching the logic from LUTs to DSPs when the number of bits reaches more than 10 bits, consuming almost 30% of an Avnet Zedboard (based on the Xilinx XC7Z020). Neither of the implementations consumes BRAMs since the PE corresponds to an operator, and no memory is needed. However, the consumption depends on the design mapping when implementing the logic into RTL and the user requirements.

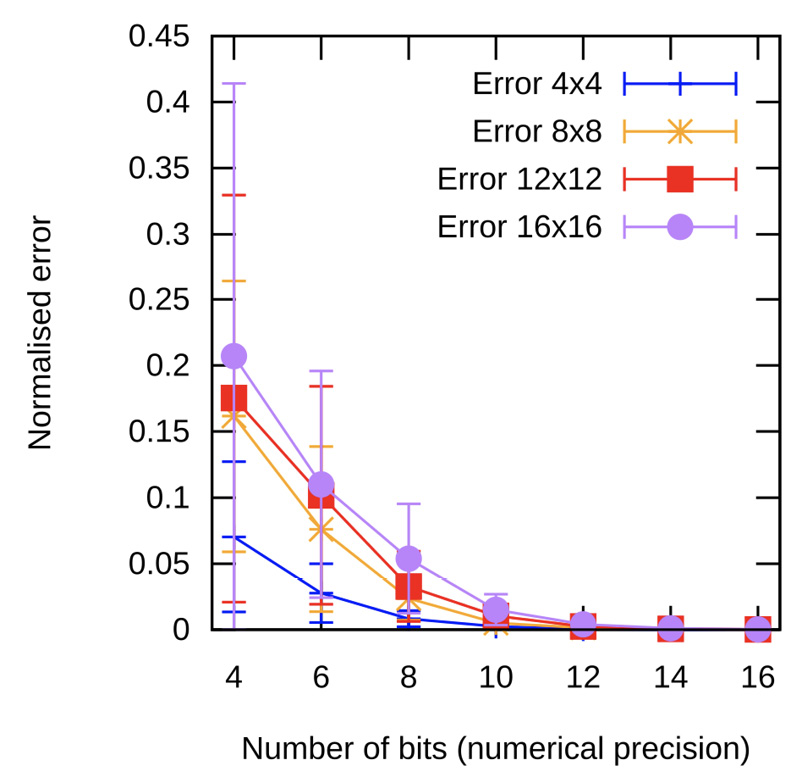
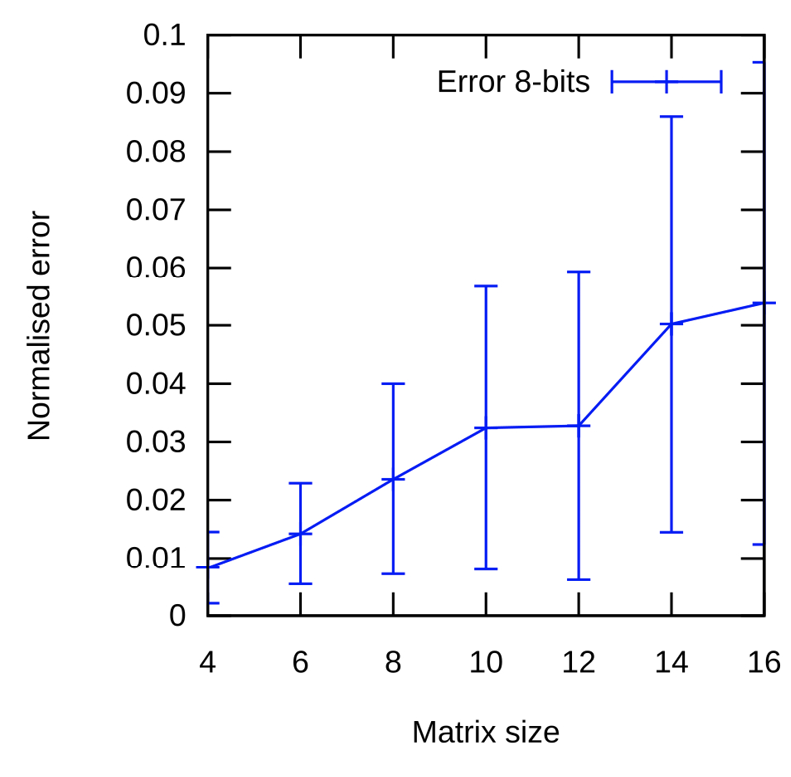
Normalised error while varying the number of bits of the fixed-point numerical representation for four matrix sizes	Normalised error while varyingø the matrix size for an 8-bits fixed-point representation

Figure 3. Resource consumption of an 8-bit fixed-point 8x8 matrix MAC. The FMA with registers results is the intermediate case in resource utilisation.

Since our FMA can specialise in arbitrary precisions, Figure 3 explores the numerical errors when tuning the numerical representation using (2). Figure 3.a shows how the error evolves as the number of bits invested increases, leading to an exponential decreasing behaviour.

The preservation of the number of bits of the output with respect to the input through the scaling of one of the registers, as described in (2), introduces a dependency on the matrix size in the error as presented in Figure 3.b. In this case, the bigger the matrix, the greater the error. It can also be noticed in Figure 3.a, showing that the most compressed precisions are heavily affected by the matrix size. A 4-bit representation scales the mean relative error from 7.5% up to 21%, having more than 40% peaks. As the number of bits increases, the error brought by the matrix size is compensated.

Conclusions

This work presented our matrix FMA as the first accelerator analysis of our deep learning inference framework for FPGAs. This framework aims to automate the generation of PEs for accelerating inference tasks while adding approximate computing to address issues concerning resource and energy consumption on low-end FPGAs. Our matrix FMA implementation shows a linear scaling in the resource consumption before less than 10 bits in the data width, showing for an 8-bit 8x8 matrix FMA a consumption of up to 11%. When having more bits, the consumption becomes constant at almost 30%, where the scaling in resource consumption becomes agnostic to the number of bits from 10 up to 16 bits. In terms of errors, we noticed the influence of the matrix size on the error, where large matrix sizes lead to high variance and coarse errors, which can be compensated by increasing the numerical precision.

In future work, we are extending the analysis in the error characterisation to get models without the need for simulations. Moreover, more PEs are being developed.

Acknowledgements

This work is supported by RidgeRun LLC, through its Master’s scholarship for collaborators, and by the Instituto Tecnológico de Costa Rica.

References

[1] C. J. Wu, D. Brooks, K. Chen, D. Chen, et al., “Machine learning at facebook: Understanding inference at the edge” Proceedings 25th IEEE International Symposium on High Performance Computer Architecture, HPCA 2019, pp. 331–344, 2019. https://doi.org/10.1109/HPCA.2019.00048

[2] B. C. Schafer and Z. Wang, “High-Level Synthesis Design Space Exploration: Past, Present, and Future” in IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 39, no. 10, pp. 2628-2639, Oct. 2020, https://doi.org/10.1109/TCAD.2019.2943570.

[3] Z. Wang and B. C. Schafer, “Learning from the Past: Efficient High-Level Synthesis Design Space Exploration for FPGAs” in ACM Transactions on Design Automation of Electronic Systems, vol. 27, no. 4, Jul. 2022, https://doi.org/10.1145/3495531.

[4] T. Liang, J. Glossner, L. Wang, S. Shi and X. Zhang, “Pruning and quantization for deep neural network acceleration: A survey”, Neurocomputing, vol. 461, pp. 370-403, 2021. https://doi.org/10.1016/j.neucom.2021.07.045

[5] T. González, J. Castro-Godínez. “Improving Performance of Error-Tolerant Applications: A Case Study of Approximations on an Off-the-Shelf Neural Accelerator” in V Jornadas Costarricenses de Investigación en Computación e Informática (JoCICI 2021), Virtual Event, Oct. 2021.

[6] Intel, “Intel® Architecture Instruction Set Extensions and Future Features”, Intel Corporation, May 2021. [Online]. Available: https://software.intel.com/content/www/us/en/develop/download/intel-architecture-instruction-set-extensions-programming-reference.html

[7] NVIDIA Corporation, “NVIDIA TESLA V100 GPU ARCHITECTURE” 2017. [Online]. Available: https://images.nvidia.com/content/volta-architecture/pdf/volta-architecture-whitepaper.pdf

[8] Andrew Lavin and Scott Gray. 2016. Fast algorithms for convolutional neural networks. In Proc. of the IEEE Conference on Computer Vision and Pattern Recognition. 4013–4021. https://doi.org/10.1109/CVPR.2016.435

[9] Salazar-Villalobos, Eduardo, and Leon-Vega, Luis G. (2022). Flexible Accelerator Library: Approximate Matrix Accelerator (v1.0.0). Zenodo. https://doi.org/10.5281/zenodo.6272004

---