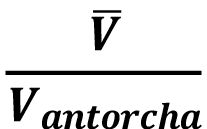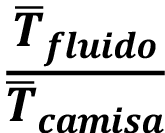Optimización del diseño de un reactor de gasificación por plasma a través de simulaciones computacionales numéricas
Design optimization of a plasma gasification reactor utilizing computational numerical simulations
Alberto Castillo-Benavides1, Gustavo Richmond-Navarro2, Esteban Zamora-Picado3, Carlos Arias-Arguedas4
Fecha de recepción: 2 de septiembre, 2022
Fecha de aprobación: 12 de diciembre, 2022
Castillo-Benavides, A; Richmond-Navarro, G; Zamora-Picado, E; Arias-Arguedas, C. Optimización del diseño de un reactor de gasificación por plasma a través de simulaciones computacionales numéricas. Tecnología en Marcha. Vol. 36, No 3. Julio-Setiembre, 2023. Pág. 34-49. https://doi.org/10.18845/tm.v36i3.6375
https://doi.org/10.18845/tm.v36i3.6375
Palabras clave
Plasma; reactor de gasificación; residuos; syngas; optimización geométrica; simulación
Resumen
El objetivo principal de esta investigación fue el desarrollo de una geometría optimizada para un reactor de gasificación de residuos municipales con plasma. Se realizó una simulación numérica de la geometría bidimensional de un reactor de gasificación por plasma con el fin de conseguir un rendimiento optimizado con el uso del software COMSOL Multiphysics. Se definieron condiciones iniciales del reactor y se crearon 16 distintas combinaciones geométricas que varían cuatro aspectos geométricos del reactor: los radios inferior y superior de la cámara de gases, la longitud central de la cámara y el volumen de la cámara de fundición. De estas, fueron halladas dos combinaciones que optimizan los aspectos de mezclado de gases y transferencia de calor hacia el ambiente. Se confirmó que los diseños planteados alcanzan las temperaturas necesarias para la fundición y gasificación de los desechos. Además, el material fundido teórico alcanza la viscosidad necesaria menor a 10 Pa s para poder fluir fuera del reactor.
Keywords
Plasma; gasification reactor; wastes; syngas; geometric optimization; simulation
Abstract
The main objective was the development of an optimized municipal waste gasification reactor geometry utilizing plasma. Here, numerical simulation utilizing the COMSOL Multiphysics software was used to achieve an optimized bidimensional geometry. Initial conditions for the reactor were defined using the researchers’ experience. Then, 16 different combinations of four geometric parameters were set, where the gas chamber’s superior, and inferior radius, it’s length and lastly the fusing chamber volume were varied. Of these, two combinations that optimized the mixing of gases and heat exchange with the exterior were found. It was confirmed that these designs allowed for the proper melting and gasification of the theoretical waste. Further, the smelted material also possessed a viscosity lower than 10 Pa s needed to flow out of the reactor.
Introducción
La gasificación de desechos sólidos es una de las tecnologías térmicas que convierte los desechos en energía aprovechable; otras opciones son la combustión y la pirolisis. En la gasificación los residuos son expuestos a temperaturas suficientemente altas (entre los 800 K y los 4000 K) lo que transforma los compuestos orgánicos en gas de síntesis que puede ser utilizado como fuente de potencia (generación de vapor, motores y celdas combustibles), sustituto de combustibles y reactivo para la fabricación de biocombustibles. Los compuestos inorgánicos son fundidos por completo, y de esta parte se recuperan metales y se produce un vitrificado inerte, no dañino con el medio ambiente, que puede ser utilizado como material para la construcción [1].
I-PLARE REACTOR (Etapa 2) fue parte de una línea de investigación la cual cuenta como antecedentes un estudio preliminar de la tecnología y su potencial para Costa Rica [2] y un proyecto de investigación previo denominado I-PLARE REACTOR, en el cual se inició formalmente el análisis de la tecnología. El proyecto I-PLARE REACTOR (Etapa 2) implementó la optimización del rendimiento del reactor de gasificación por plasma desarrollado en I-PLARE REACTOR (Etapa 1). Esta optimización se enfocó en el rediseño geométrico parametrizado para determinar las características geométricas óptimas del reactor con la finalidad de mejorar su rendimiento, además de una caracterización del funcionamiento del reactor considerando variaciones en la composición de residuos de alimentación. El proceso de optimización se realizó a través de simulaciones computacionales de dinámica de fluidos (CFD, por sus siglas en inglés) utilizando el software COMSOL Multiphysics.
Algunos autores como [3] destacan que una comprensión profunda de los flujos y la química, obtenidos a través del modelado computacional, puede ayudar en gran medida el proceso de diseño. Los trabajos de simulación CFD han demostrado ser un medio eficaz para el análisis de diseño y la optimización de procesos de conversión de energía [4], [5], [6], [7], [8], y en particular para la gasificación por plasma térmico [1], [9], [10], donde ahorra costos económicos y permite tener acceso a datos que ni siquiera podrían ser medidos experimentalmente.
Marco teórico
Ante la creciente producción de los residuos sólidos urbanos (RSU) y residuos industriales peligrosos se han propuesto varios procesos térmicos que permitan la destrucción de la parte orgánica de los residuos y la conversión del sobrante inorgánico en un residuo inerte, reutilizable, que no sea dañino para el ambiente y que no tenga que ser almacenado en un vertedero de residuos. La incineración, pirolisis, fundición o vitrificación, son algunos ejemplos de estos procesos [11]. Los plasmas térmicos fueron utilizados durante mucho tiempo únicamente para destruir desechos peligrosos y en procesos industriales. Sin embargo, debido al creciente interés en tecnologías que permitan aprovechar la energía latente en los desechos (“waste-to-energy processes” [12]) se han desarrollado varias tecnologías que permiten obtener gas de síntesis (syngas) de los residuos sólidos, una de ellas es la gasificación por plasmas térmicos [12].
Según [13] la gasificación es una tecnología de proceso que está diseñada con el propósito de producir gas de síntesis a través de la conversión química de los materiales carbonosos en un proceso que implica la oxidación parcial de materiales. Este proceso se lleva a cabo en una atmósfera reductora en presencia de un agente gasificante, a temperaturas suficientemente altas para convertir la materia inorgánica a un material sólido vítreo.
Los gasificadores por plasma térmico presentan varias ventajas en comparación con tecnologías convencionales: altos rendimientos con reactores relativamente compactos, altas tasas de enfriamiento y calentamiento (>106 K/s), bajos flujos de gases de escape y gran facilidad para fundir los residuos inorgánicos [11]. Por otro lado, aunque la viabilidad económica de este tipo de tecnologías ya ha sido demostrada, una de las grandes desventajas es el alto costo de inversión inicial para la puesta en marcha de una planta de tratamiento de este tipo [14].
La simulación numérica mediante la dinámica de fluidos computacional (CFD), es un medio eficaz para el análisis y la optimización de los procesos de conversión de energía [4]. En [15] han utilizado aplicaciones actuales de la herramienta de CFD en el diagnóstico de los sistemas de incineración de residuos y la evaluación de los cambios en las condiciones de funcionamiento. En [4] se ha realizado el estudio en detalle de los modelos CFD de la capa de combustión fluidizado burbujeante de plantas de conversión de residuos en energía y demostraron que los modelos en 3-D basados en CFD pueden predecir con éxito el comportamiento del sistema de combustión de lecho fluidizado. En un estudio similar, [5] demuestra que las simulaciones CFD pueden proporcionar información fundamental sobre la naturaleza de las características de flujo y el subsiguiente patrón de flujo de gas en la cámara de reacción de un gran incinerador de residuos sólidos municipales. Varios otros estudios ( [6], [7], [8] y [16]) han señalado que la simulación numérica mediante CFD se puede utilizar con eficacia en la evaluación del diseño y optimización de procesos de conversión de residuos en energía.
En [1] se plantea un modelado matemático para el proceso del reactor de Yblin, Israel, el cual se pudo validar a través de mediciones experimentales. Su trabajo comprendió el desarrollo de un modelo 0-dimensional para la compresión del proceso químico al interior del reactor y un modelado 2-dimesional que comprendía la interacción de los fluidos dentro del reactor, las reacciones químicas y la transferencia de calor. Además, se consideraron variaciones en parámetros como: flujos de aire secundario, potencia de las antorchas de plasma y alimentación de vapor de agua sobrecalentado al proceso. Su trabajo logró definir un rango de parámetros de operación bajo los cuales se logra extraer un gas de síntesis con un mayor valor calorífico (LHV por sus siglas en inglés). Gracias a la simulación numérica del modelo planteado por Zhang, la optimización de los parámetros de operación del reactor fue posible y brindó un mejor entendimiento del proceso.
En la fase previa a esta investigación, [17] implementó un modelo computacional basado principalmente en los trabajos de [1], en el cual se incorporaba la dinámica de fluidos, la transferencia de calor y el transporte de especies diluidas para modelar el reactor en diseño. Se utilizaron los resultados de [1] para validar sus modelos y con base en ellos, analizó el diseño existente de reactor en ese momento y valoró la variación de ciertos parámetros geométricos y térmicos del proceso. Se logró determinar, para el diseño propuesto, cuáles parámetros tenían poca influencia en el rendimiento del reactor y cuales tenían gran influencia.
En esta misma fase previa, [18] implementó otro modelo computacional en donde incluía la dinámica de fluidos, la transferencia de calor y además el transporte de especies concentradas basado principalmente en el trabajo previo de [10], validando sus resultados contra esta misma referencia.
Tanto el trabajo de [17], como el de [18] forman la base común de la presente investigación a nivel de modelos computacionales, donde los aspectos comunes a ambos trabajos se resumen, en el caso de los reactores ideales, al conjunto de modelos representados por las ecuaciones (1k), (2i), (3), (4), (5), (6) y (7).
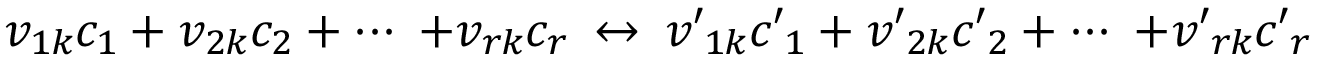 (1k)
(1k)
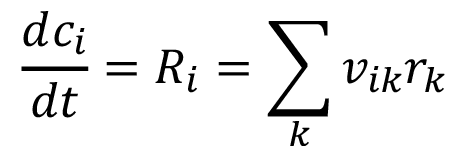 (2i)
(2i)
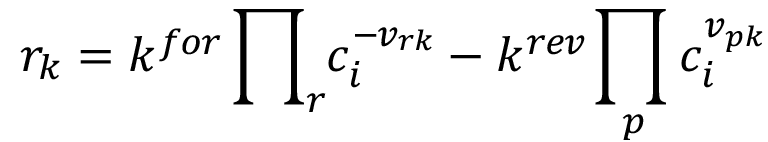 (3)
(3)
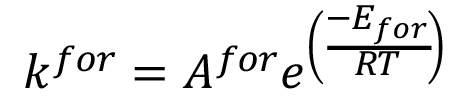 (4)
(4)
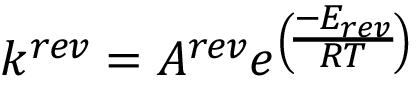 (5)
(5)
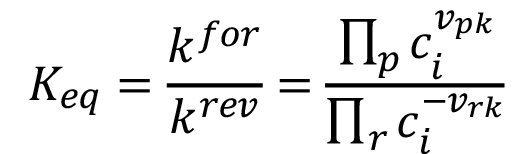 (6)
(6)
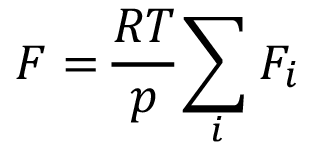 (7)
(7)
En el caso de los reactores no ideales, ambos trabajos coinciden en la mayoría de aspectos y los modelos comunes son representados por (8), (9), (10), (11), (12), (13), (14), (15), y (16).
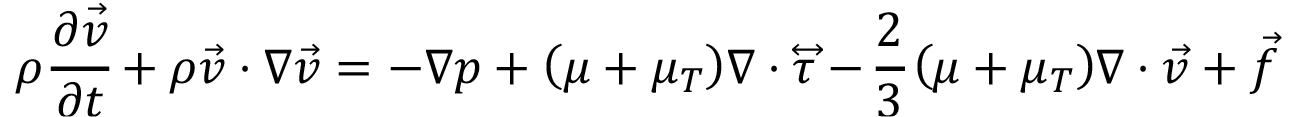 (8)
(8)
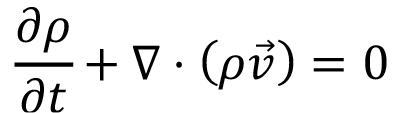 (9)
(9)
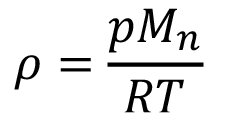 (10)
(10)
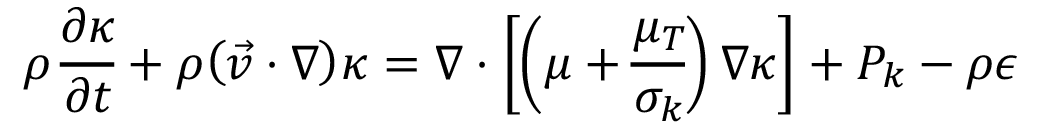 (11)
(11)
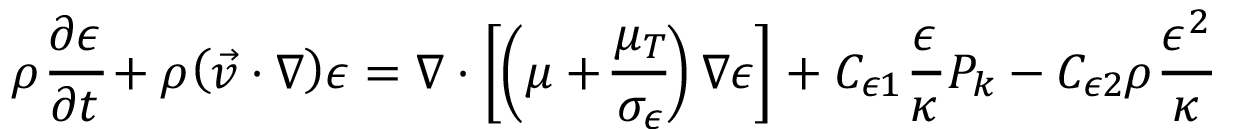 (12)
(12)
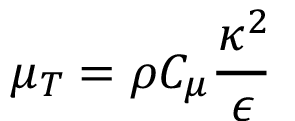 (13)
(13)
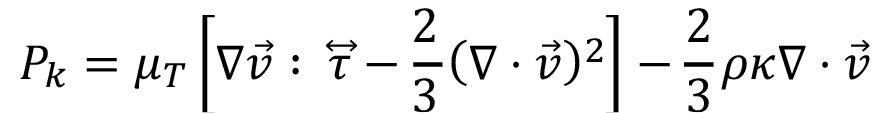 (14)
(14)
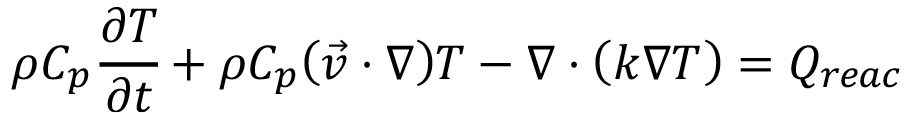 (15)
(15)
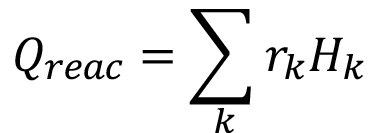 (16)
(16)
Cabe destacar que el presente modelo permite estimar la composición de gases de síntesis en conjunto con la variabilidad de las familias de componentes químicos presentes en los residuos sólidos municipales. Este modelo se basa no solo en los compuestos biomásicos, sino también en especies plásticas que pueden estar presentes.
Finalmente, la tecnología de gasificación ha demostrado ser un medio eficiente para lograr procesos de conversión de desechos en fuentes energéticas utilizables, un ejemplo de ello es el gas de síntesis. Esta tecnología contribuye a la reducción de grandes volúmenes de desechos que, de otra manera, deberían ser depositados en un vertedero a cielo abierto. El proceso de gasificación de desechos sólidos envuelve fenómenos químicos y físicos muy complejos (ecuaciones 1-16), sensibles a cambios por variaciones en la geometría del reactor, la potencia de las antorchas y los flujos de alimentación y extracción de las materias. Las simulaciones computacionales de la mecánica de fluidos son una herramienta que permite comprender estos fenómenos y optimizar las variables del proceso y la geometría de los reactores de gasificación con la finalidad de alcanzar procesos cada vez más eficientes, que permitan reducir costos y obtener gas de síntesis de un grado energético más alto.
Materiales y métodos
Se establecieron, en orden de prioridad, las variables geométricas a optimizar para el diseño nuevo planteado por el grupo comparándolas con los procesos de optimización presentes en la literatura y tomando en cuenta los puntos de mejora del diseño presentado en la etapa 1 del proyecto I-PLARE REACTOR. Se estableció como criterios de optimización la obtención de la mayor temperatura promedio de la fase gaseosa para asegurar condiciones cercanas al equilibrio químico y la mayor velocidad promedio en el dominio gaseoso del reactor con el fin de asegurar el mezclado de las especies gaseosas presentes, así como el mayor poder calorífico inferior del syngas obtenido. Se crearon los modelos 2D del reactor con las diferentes variaciones geométricas a evaluar en AutoCAD. Se implementó el modelo matemático con las respectivas condiciones de frontera, en el modelo 2D del reactor y se realizaron las simulaciones utilizando COMSOL Multiphysics. Las simulaciones se realizaron considerando los módulos de dinámica de fluidos, químicos y transporte de especies utilizados y consideraciones de los trabajos previos [17] y [18]. Con base en los criterios de optimización indicados anteriormente, se analizaron los datos brindados por las simulaciones y se determinó la geometría óptima para el diseño del reactor.
El proyecto I-PLARE REACTOR (etapa 1) permitió una primera aproximación al grupo de investigadores al tema del modelado y al diseño del reactor en varios aspectos generales y otros específicos. Respecto a los específicos es importante retomar algunos de ellos:
Respecto al diseño del reactor desarrollado por [19] se indica que esencialmente consiste en un escalamiento geométrico del reactor de [1] considerando la taza de consumo de RSU de 1 a 2 toneladas diarias. Si bien los análisis realizados por [17] y [18] avalan el funcionamiento de ese diseño de reactor de gasificación, este último indica varias opciones de mejora tales como incluir más consideraciones operativas y prácticas en el diseño, así como apuntar a un diseño más compacto con menos pérdidas de energía dado el tipo de tecnología, pero principalmente por la taza de procesamiento del reactor. El presente grupo de trabajo considerando estas recomendaciones, y de igual forma, otras tales como incluir más variables geométricas de diseño, incluir más aspectos relacionadas con el proceso químico y termodinámico, y retroalimentándose con experiencia proveniente de la industria, optó por plantear una nueva geometría, configuración de reactor y materiales obteniendo un diseño base que posteriormente fue optimizado geométricamente.
Respecto al modelo computacional del reactor desarrollado por [17] y [18] los cuales corresponden a implementaciones locales de los trabajos de [1] y [10] respectivamente, ambos indican posibilidades de mejora en sus modelos, lo cual se tomó en cuenta de la siguiente manera: la mejora en el modelo de turbulencia, en la inclusión del dominio sólido (aislantes de la cámara interna) y líquido (cámara de fundición) y una ampliación de la materia prima que el reactor puede admitir en su ingreso dada la ampliación de las especies químicas consideradas en el modelo computacional. Algunas consideraciones al final no fueron tomadas en cuenta por la alta razón costo/beneficio (se presentaban problemas de convergencia al realizar acoples multifísicos, lo cual aumentaba la no linealidad del grupo de ecuaciones del modelo computacional) que implicaba incluirlas en el modelo. Estos son los casos de las reacciones heterogéneas de múltiples fases e inclusión de los RSU propiamente como una fase sólida que pasaba a gaseosa. Una consideración que sí se incluyó parcialmente fue incluir la transferencia de calor por radiación en el modelo, pero al considerarse simultáneamente con las reacciones químicas resultó tener un impacto poco significativo, pero sí un aumento considerable en las demandas computacionales, lo que llevó a descartar su inclusión en los modelos finales.
En el diseño del reactor de gasificación estudiar el comportamiento de los fluidos y el calor es esencialmente obligatorio, permitiendo evaluar la eficacia de la geometría en transferir la energía para asegurar la presencia de equilibrios termodinámicos que permitan la conversión completa de las reacciones principales del proceso de gasificación y generación de syngas. Por tanto, el modelo básicamente se limita a un sistema gaseoso y otro líquido a alta temperatura, con el fin de separar el proceso de gasificación en dos principales procesos, el primero la epata de volatilización rápida del RSU por las antorchas de plasma gobernado por fluidos gaseosos de alta temperatura y una segunda etapa de fundición de metales y escorias dentro de la sección de fundición en la parte baja del reactor.
Geometría
La simulación numérica permite evaluar modelos geométricos en cero, una, dos o tres dimensiones para comprender y predecir el flujo de los fluidos y el calor. El proceso de simulación inicia definiendo la geometría del reactor, la cual se puede separar en tres etapas de operación (ver Figura 1), en específico:
•Etapa 1 – Descomposición térmica del RSU: Relacionada con la trayectoria seguida por los materiales a gasificar, que generalmente tienen exceso de humedad y están a temperaturas muy inferiores a los necesarios para que ocurra la gasificación. Resulta necesario incrementar su temperatura transfiriendo calor de las paredes del reactor y de los gases generados en la siguiente etapa.
•Etapa 2 - Gasificación: En esta etapa se da la gasificación de los desechos, ya sea en las instancias de las paredes del gasificador o al interactuar con el fundido y los gases calientes de la antorcha de plasma.
•Etapa 3 - Fundición: Es una fase fundida, alimentada con las cenizas de los desechos, las que a su vez se encapsulan en un vitrificado.
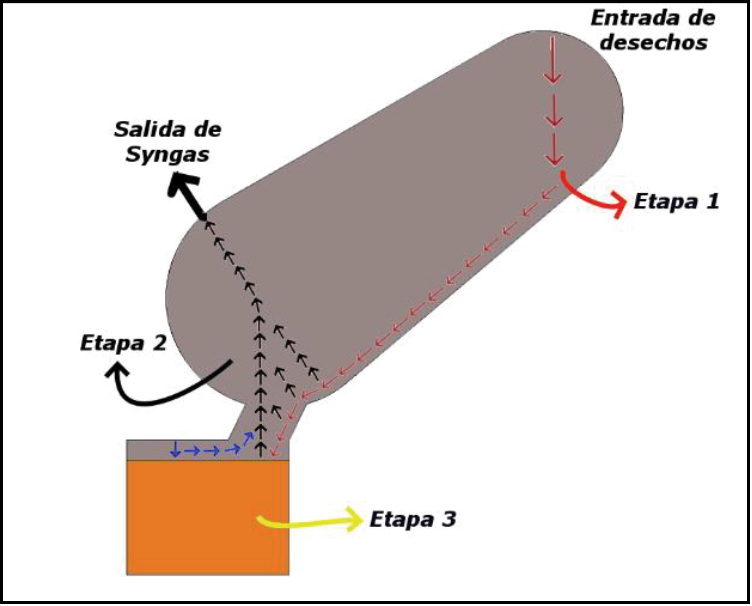
Figura 1. Geometría del sistema de gasificación propuesto y sus etapas.
Es muy importante notar que la Figura 1 representa los primeros planteamientos geométricos del reactor, pero esta geometría fue cambiada cuando se notaron las necesidades calóricas elevadas en la cámara de fundición. A partir de la Figura 4 se notará que la entrada de los desechos se da por el lado de la cámara inferior de fundición y la salida del Syngas sucede por la parte superior del reactor.
Una vez superado el proceso de planteo de la geometría del reactor es necesario evaluar su funcionamiento simulando numéricamente los principales fenómenos fluidodinámicos y térmicos con el fin de observar el comportamiento de los gases en la geometría y evaluar las variables que permitirán mejorar el diseño y maximizar su desempeño.
Para su modelado y posterior simulación, no se toma en cuenta los desechos sólidos previos a su gasificación, principalmente por la complejidad que conllevaría asumir una simulación de este tipo, y por lo tanto el modelo se simplifica en dos dominios, como se muestra en la Figura 2.
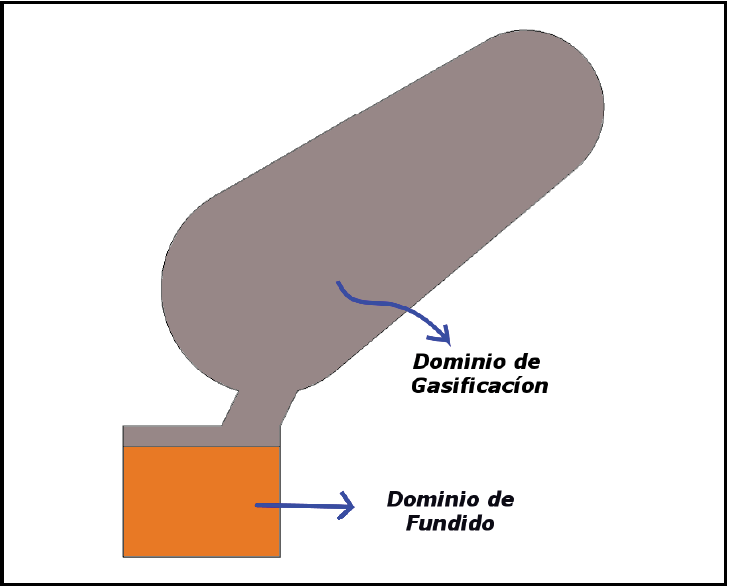
Figura 2. Modelo geométrico del reactor.
•Dominio de gasificación: como se observa en la Figura 2 representa el mayor volumen en el sistema y se modela como un fluido compuesto por los gases calientes de la antorcha de plasma y el gas generado del sólido por gasificación.
•Dominio de fundición: Consiste en un fluido vítreo, cuyas temperaturas deberían permanecer alrededor de 1200 K. La transferencia de calor para mantener el material fundido debe realizarse en gran medida desde los gases calientes de la antorcha de plasma, pero también de igual forma con electrodos eléctricos internos para reducir el enfriamiento interno y eventuales estancamientos.
Modelos físicos y matemáticos
En el modelamiento físico y matemático de un sistema como el dominio de gasificación se debe incluir principios básicos como la conservación de energía, la masa y el momento. Del estudio en conjunto de estos tres fenómenos y asumiendo que el fluido objeto de estudio es del tipo newtoniano y compresible, las ecuaciones de Navier-Stokes siguen tomando la forma de las ecuaciones (8), (9) y (10) consideradas en el modelo base de [18].
Es necesario incluir el efecto de la turbulencia en los gases, lo cual en este nuevo trabajo constituye una mejora del modelo base, ya que se considera un modelo más elaborado que el modelo κ-ω de [20]. De esta forma las ecuaciones (11, 12 y 13) son sustituidas por sus formas primadas (11’, 12’ y 13’):
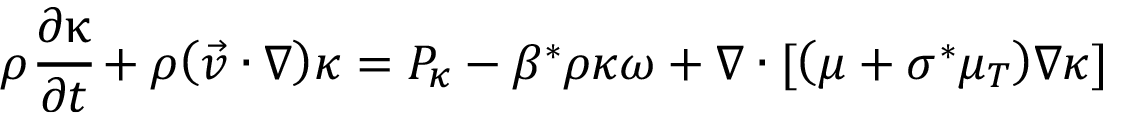 (11’)
(11’)
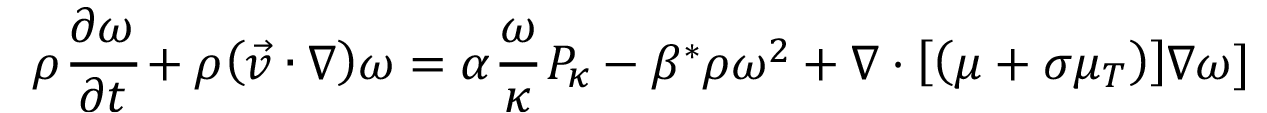 (12’)
(12’)
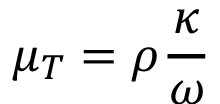 (13’)
(13’)
Donde la energía cinética turbulenta κ, la tasa de disipación específica ω y la viscosidad de Eddy μT se calculan de acuerdo con esas ecuaciones. Pκ se sigue calculando de la misma forma (ecuación 14), pero además de eso es necesario incorporar los coeficientes de cierre para el modelo [20].
 (14’)
(14’)
En relación con la transferencia de calor en el dominio de gasificación y fundición, se estudian los mecanismos de conducción y convección, por medio de las ecuaciones para la ley de Fourier y de balance de energía. Para el dominio de fundición se aproxima como un sólido, por lo que el mecanismo de transferencia es conducción y el modelo matemático permanece igual a la ecuación anterior.
Planteamiento del diseño de experimentos para el estudio del diseño de la geometría del reactor
El diseño de la geometría se realiza de forma colaborativa tomando en cuenta la experiencia en sistemas de gasificación, manejo de sólidos, diseño mecánico, ingeniería en materiales y previas investigaciones del equipo investigador, cuya propuesta inicial fue la geometría de la Figura 1. De esta nueva geometría se identifican los parámetros geométricos que podrán tener una incidencia sobre el desempeño del reactor, se detallan en el Cuadro 1.
Cuadro 1. Parámetros geométricos del modelo.
|
Parámetro |
Unidades |
Valor |
Descripción |
|
S |
(cm) |
0 |
Separación de la salida respecto al punto de tangencia |
|
D ent |
(cm) |
10 |
Diámetro de entrada |
|
D syn |
(cm) |
10 |
Diámetro de salida del syngas |
|
D sal |
(cm) |
15 |
Diámetro de la salida inferior |
|
β inclinación |
(°) |
35 |
Inclinación |
|
delta |
(°) |
65 |
Inclinación de la conexión entre módulos |
|
Base |
(cm) |
40 |
Base de la cámara de fundición |
|
D antorcha |
(cm) |
1 |
Diámetro de la antorcha |
|
S antorcha |
(cm) |
4 |
Separación de la antorcha respecto del borde |
|
H gases |
(cm) |
5 |
Alto de cámara de gasees en módulo de fundición |
|
H vidrio |
(cm) |
10 |
Alto del sector lleno de vidrio fundido |
|
D slag |
(cm) |
1 |
Diámetro de salida del slag |
|
D ash |
(cm) |
1 |
Diámetro de entrada de ceniza |
En la Figura 3 se presentan estos parámetros de forma visual.
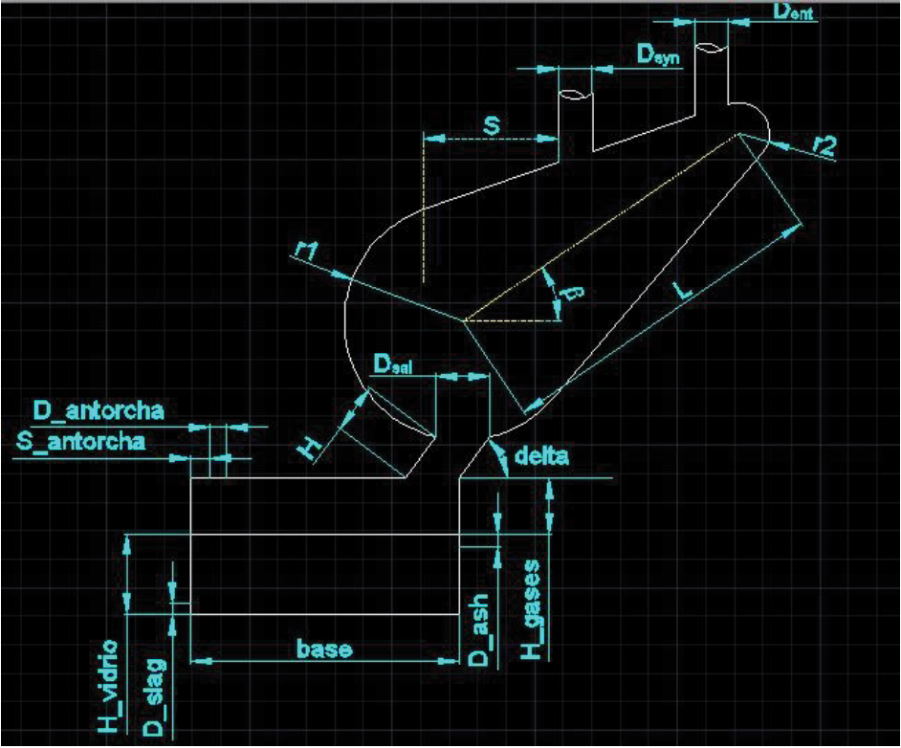
Figura 3. Todos los posibles parámetros a dimensionar en el volumen interno del reactor.
Las condiciones iniciales de la simulación, así como los niveles a los que serán probados los parámetros R1, R2, L y H se presentan en el Cuadro 2.
Cuadro 2. Condiciones iniciales para el modelado del sistema de gasificación.
|
Condición |
Unidades |
Valor |
Descripción |
|
P inicial |
(Pa) |
0 |
Presión inicial del sistema |
|
U inicial |
(m/s) |
0 |
Velocidad inicial del sistema |
|
U 0 antorcha |
(m/s) |
15 |
Velocidad salida de gases de antorcha |
|
P 0 gases desechos |
(Pa) |
0 |
Presión inicial de salida de gases |
|
U 0 gases desechos |
(m/s) |
0,8 |
Velocidad de entrada de gases de desechos |
|
T inicial del sistema |
(K) |
600 |
Temperatura inicial del sistema |
|
T antorcha |
(K) |
2500 |
Temperatura de antorcha |
|
T desechos |
(K) |
450 |
Temperatura de desechos |
|
P b potencia fundida |
(W) |
5000 |
Potencia suministrada al fundido |
|
T ext |
(K) |
293,15 |
Temperatura externa |
|
R1 |
(cm) |
0,25 – 0,3 |
Radio inferior cámara de gases |
|
R2 |
(cm) |
0,1 – 0,2 |
Radio superior cámara de gases |
|
L |
(cm) |
0,7 – 0,8 |
Longitud central cámara de gases |
|
H |
(cm) |
5 - 15 |
Longitud de la sección de conexión entre la región de gasificación y fundición |
Con este gran número de parámetros se plantea un diseño de experimentos del tipo 24 con tratamientos R1 R2 L y H para determinar el conjunto de combinaciones que maximizan el mezclado de los gases y minimiza la transferencia de calor hacia el exterior del reactor. Como variables a impactar se establecen la velocidad promedio de los fluidos dentro del reactor (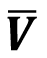 ), la temperatura promedio del fluido (
), la temperatura promedio del fluido ( ) y la temperatura promedio en la carcasa externa del aislante térmico del reactor (
) y la temperatura promedio en la carcasa externa del aislante térmico del reactor (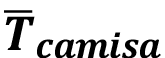 ), para las condiciones iniciales del Cuadro 2. Este diseño de experimentos, con cada una de las pruebas a realizar se detalla en el Cuadro 3.
), para las condiciones iniciales del Cuadro 2. Este diseño de experimentos, con cada una de las pruebas a realizar se detalla en el Cuadro 3.
Cuadro 3. Diseño de experimentos empleado para los parámetros a variar.
|
Prueba |
R1 (cm) |
R2 (cm) |
L (cm) |
H (cm) |
|
1 |
25 |
10 |
70 |
5 |
|
2 |
25 |
10 |
70 |
15 |
|
3 |
25 |
10 |
80 |
5 |
|
4 |
25 |
10 |
80 |
15 |
|
5 |
25 |
20 |
70 |
5 |
|
6 |
25 |
20 |
70 |
15 |
|
7 |
25 |
20 |
80 |
5 |
|
8 |
25 |
20 |
80 |
15 |
|
9 |
30 |
10 |
70 |
5 |
|
10 |
30 |
10 |
70 |
15 |
|
11 |
30 |
10 |
80 |
5 |
|
12 |
30 |
10 |
80 |
15 |
|
13 |
30 |
20 |
70 |
5 |
|
14 |
30 |
20 |
70 |
15 |
|
15 |
30 |
20 |
80 |
5 |
|
16 |
30 |
20 |
80 |
15 |
Con estas pruebas definidas, se procede a realizar la simulación de cada una de ellas con el objetivo de encontrar la configuración óptima del reactor.
Resultados y discusión
Resultados térmicos y de los fluidos
En esta sección se presentan los resultados junto con su discusión correspondiente de las simulaciones realizadas. Primero, se presentan en el Cuadro 4 los resultados numéricos de las variables a medir (definidas adelante) junto con el cálculo de un indicador que maximiza el desempeño deseado del reactor. Posteriormente, se realiza un análisis de los campos de velocidad y temperatura de las configuraciones que resulten óptimas.
Las variables medidas para cada una de las pruebas de los reactores simulados son las siguientes: 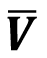 : Velocidad promedio,
: Velocidad promedio,  : Temperatura del fluido,
: Temperatura del fluido, 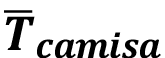 :Temperatura de la camisa,
:Temperatura de la camisa,  : Velocidad de la antorcha. Con estas mediciones se obtienen las relaciones de
: Velocidad de la antorcha. Con estas mediciones se obtienen las relaciones de 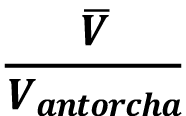 y
y 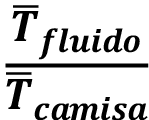 junto con el indicador
junto con el indicador 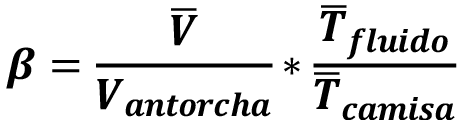 . Ambas de estas relaciones junto con el indicador se desean maximizar.
. Ambas de estas relaciones junto con el indicador se desean maximizar.
Además, la primera de estas relaciones busca maximizar el mezclado de los gases, la segunda de estas minimiza la transferencia de calor hacia el ambiente y el indicador representa la configuración que tendrá la mejor relación respecto a mezclado y pérdidas de calor al exterior.
Cuadro 4. Resultados de las diferentes configuraciones empleadas.
|
Prueba |
(m/s) |
(K) |
(K) |
|
|
Indicador b |
|
1 |
5,296 |
1922,8 |
1708,1 |
0,211 840 |
1,125 695 |
0,238 467 |
|
2 |
5,1591 |
1948,2 |
1706,5 |
0,206 364 |
1,141 635 |
0,235 592 |
|
3 |
5,2023 |
1930,2 |
1705,4 |
0,208 092 |
1,131 817 |
0,235 522 |
|
4 |
5,0289 |
1955,3 |
1700,2 |
0,201 156 |
1,150 041 |
0,231 338 |
|
5 |
4,9763 |
1930,1 |
1686,2 |
0,199 052 |
1,144 645 |
0,227 844 |
|
6 |
4,8047 |
1968,1 |
1698,0 |
0,192 188 |
1,159 069 |
0,222 759 |
|
7 |
4,8053 |
1923,9 |
1672,1 |
0,192 212 |
1,150 589 |
0,221 157 |
|
8 |
4,6197 |
1968,9 |
1687,3 |
0,184 788 |
1,166 894 |
0,215 628 |
|
9 |
5,2192 |
1939,8 |
1688,3 |
0,213 168 |
1,148 966 |
0,244 923 |
|
10 |
5,0814 |
1960,6 |
1701,2 |
0,203 256 |
1,152 481 |
0,234 249 |
|
11 |
5,2731 |
1953,2 |
1692,5 |
0,210 924 |
1,154 032 |
0,243 413 |
|
12 |
4,9295 |
1970,4 |
1689,8 |
0,197 180 |
1,166 055 |
0,229 923 |
|
13 |
4,9099 |
1937,9 |
1666,8 |
0,196 396 |
1,162 647 |
0,228 339 |
|
14 |
4,7159 |
1974,1 |
1680,8 |
0,188 636 |
1,174 500 |
0,221 553 |
|
15 |
4,7248 |
1940,3 |
1658,9 |
0,188 992 |
1,169 630 |
0,221 051 |
|
16 |
4,5395 |
1982,1 |
1679,4 |
0,181 580 |
1,180 243 |
0,214 309 |
Magnitud de velocidad de los gases y campo vectorial de velocidades
En las siguientes figuras (Figura 4 y Figura 5) se muestra el campo de velocidades generado por el flujo de los gases en el reactor. Se puede observar como los gases de la antorcha al incidir sobre el fundido y mezclarse con los gases de los desechos sólidos transfieren su calor, incrementando su temperatura como se observa en la Figura 6 y de igual manera la magnitud de la Figura 5.
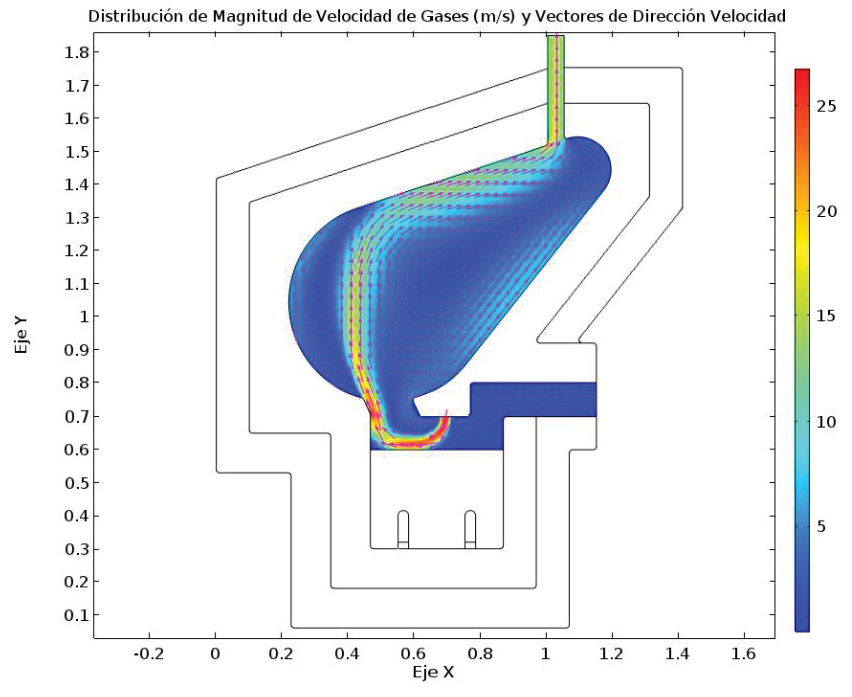
Figura 4. Resultados del campo de velocidad en la configuración 9.
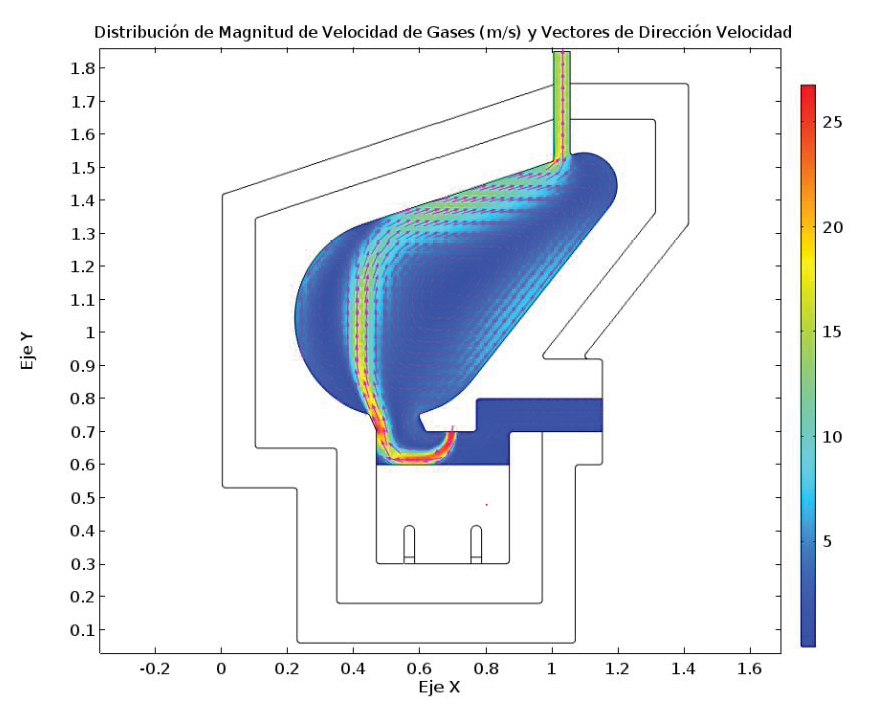
Figura 5. Resultados del campo de velocidad en la configuración 16.
Notar que a partir de esta Figura 4 se da el cambio en la geometría y la entrada de desechos del reactor. El cambio se llevó a cabo luego de algunas pruebas preliminares de CFD y calor sobre la cámara de fundición. Con estas pruebas se concluyó que era necesario realizar la alteración y una inclusión adicional de dos electrodos de fundición, los cuales constituyen elementos de calefacción (estos electrodos también son utilizados en la industria de fundición de vidrio).
De la Figura 6 se destaca como los gases en la cámara tienen una temperatura alta y su distribución es bastante uniforme, comparando con los gases generados por los desechos sólidos. Esto evidencia que sí hay una adecuada transferencia de energía.
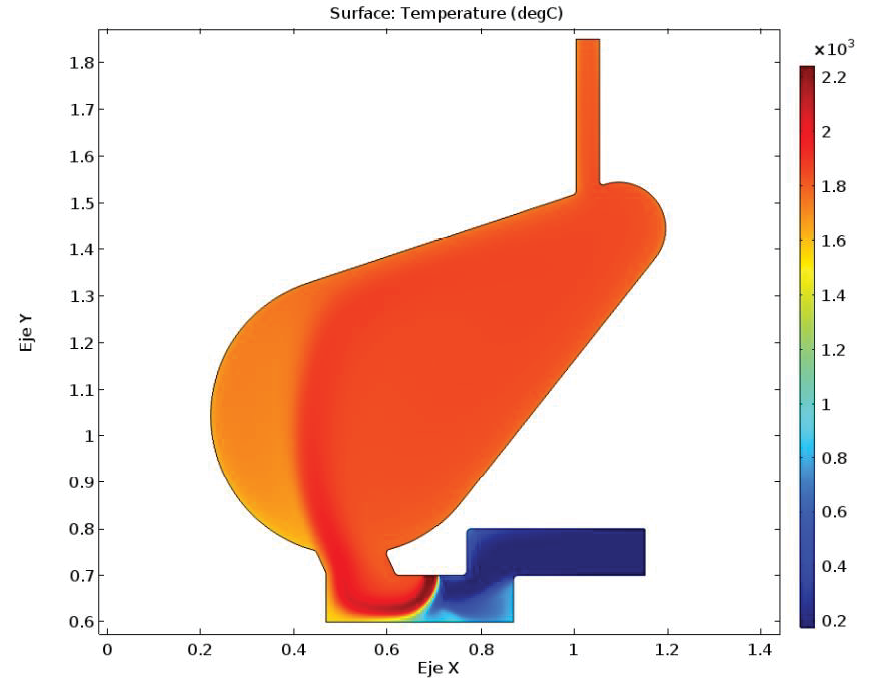
Figura 6. Resultados del campo de temperatura de la configuración 9, para del dominio fluido.
En relación con la pérdida de energía por conducción hacia el ambiente, la Figura 7 muestra la distribución de la temperatura para la configuración 16, cuyas variantes presentaron el mejor desempeño en cuanto a la transferencia de calor hacia las capas externas del aislante térmico, en donde las temperaturas alcanzan los alrededores de los 240 °C.
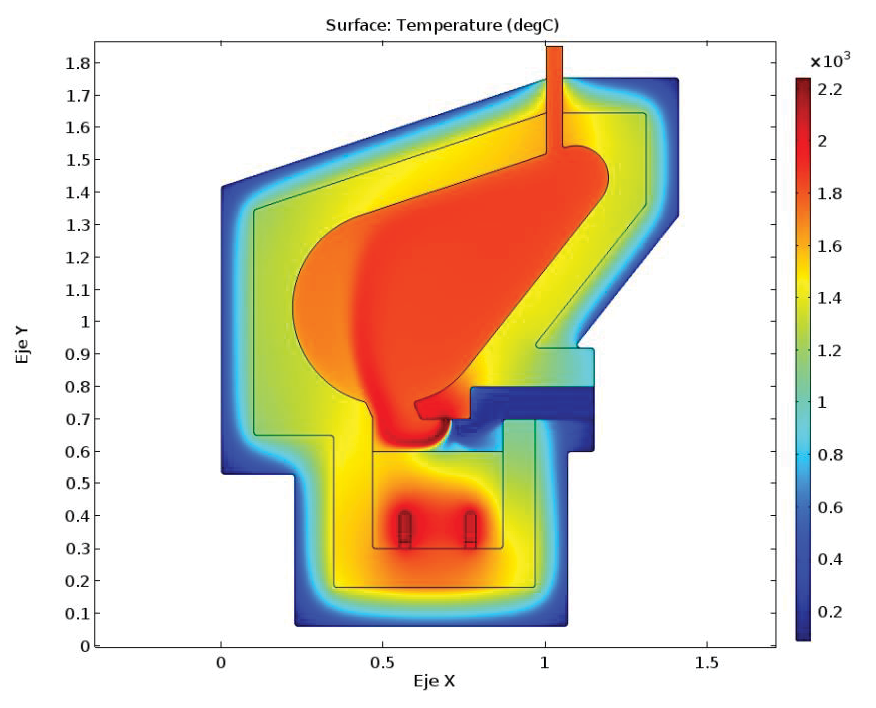
Figura 7. Resultados del campo de temperatura en la configuración 16 para todo el dominio.
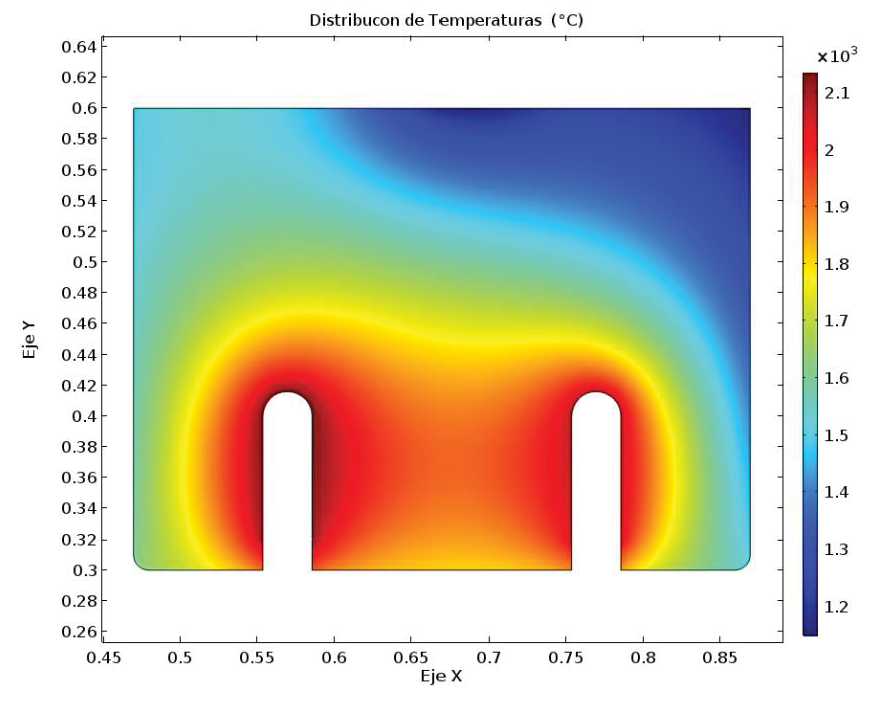
Figura 8. Resultados del campo de temperatura para el dominio del fundido en la configuración 16.
Para el dominio del fundido, el análisis se centra en el hecho de que el material debe alcanzar temperaturas de alrededor de 1200 °C, para lograr establecer una viscosidad menor a 10 Pa s. Así, el fundido podrá fluir por si solo fuera de la cámara. Para lograr esto último se incluyeron dos regiones de calentamiento simulando electrodos de fundición, práctica muy común en la industria de fundición de vidrio.
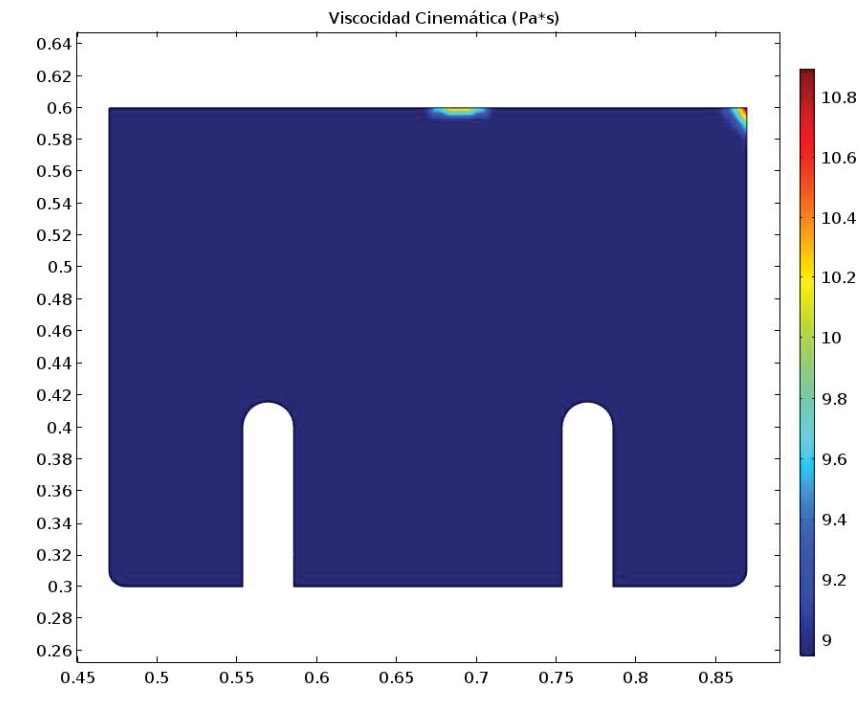
Figura 9. Resultados del campo de viscosidad para el dominio del fundido.
En la Figura 8 se muestra como el fundido alcanza temperaturas mayores a 1200 °C en todo el dominio, lo que permite afirmar que el material se encontrará a una viscosidad centrada en 10 Pa s en general, y específicamente con su mayoría de volumen en viscosidad menores a 9,2 Pa s como se observa en la Figura 9. Nótese de igual forma la uniformidad, lo cual es un resultado deseado para evitar solidificación y atascamiento.
Conclusiones
Con base en lo evidenciado en la sección de resultados y discusión, se pueden obtener las siguientes conclusiones respecto a la optimización de la geometría del reactor:
Se establece que la configuración 9 del diseño experimental desarrollado maximiza el mezclado de los gases con un indicador de razón de velocidades de 0,213.
Se establece que la configuración 16 minimiza la transferencia de calor hacia el ambiente con un indicador de temperaturas igual a 1,180.
Se establece que la configuración 9 del diseño experimental brinda el mejor desempeño en cuanto a la relación de mezclado y pérdidas de calor hacia el exterior con un indicador Beta de 0,245.
El diseño propuesto y su condición de operación permiten transferir la energía necesaria al material inorgánico para lograr su fundición y alcanzar una distribución de temperatura mínima de 1200 °C, lo cual permite alcanzar el equilibrio termodinámico de las reacciones químicas propuestas en el modelo cinético.
El campo de temperaturas de las simulaciones obtenidas, indica que el suministro de calor debido a las antorchas y electrodos de fundición permiten alcanzar viscosidades en el material fundido menores a 10 Pa s, lo cual permite su flujo hacia el exterior de la cámara de fundición.
Referencias
[1] Q. Zhang, L. Dor, A. Biswas, W. Yang y W. Blasiak, «Modeling of steam plasma gasification for municipal solid waste.,» Fuel processing technology, nº 106, pp. 546-554, 2013.
[2] V. Vargas y S. Tallents, «Determinación del potencial y los requerimientos para aplicar la tecnología de gasificación por plasma en el tratamiento de desechos y la producción de energía eléctrica en el país.,» Instituto Tecnológico de Costa Rica, Cartago, 2012.
[3] J. Heberlein y A. Murphy, «Thermal plasma waste treatment,» Journal of physics D: Applied Physics, vol. 41, nº 5, p. 053001, 2008.
[4] S. Ravelli, A. Perdichizzi y G. Barigozzi, «Description, applications and numerical modelling of bubbling fluidized bed combustion in waste-to-energy plants.,» Progress in Energy and Combustion Science, vol. 34, nº 2, pp. 224-253, 2008.
[5] C. Ryu, Y. Yang, V. Nasserzadeh y J. Swithenbank, «Thermal reaction modeling of a large municipal solid waste incinerator,» Combustion Science and Technology, vol. 176, nº 11, pp. 1891-1907, 2004.
[6] C. Ryu y S. Choi, «3-dimensional simulation of air mixing in the MSW incinerators,» Combustion Science and Technology, vol. 119, nº 1-6, pp. 155-170, 1996.
[7] C. Ryu, D. Shin y S. Choi, «Combined simulation of combustion and gas flow in a grate-type incinerator,» Journal of the Air & Waste Management Association, vol. 52, nº 2, pp. 189-197, 2002.
[8] C. Goddard, Y. G. J. Yang, V. Sharifi, J. Swithenbank, J. Chartier y S. Moseley, «Optimization study of a large waste-to-energy plant using computational modelling and experimental measurements.,» Journal of the Energy Institute, vol. 78, nº 3, pp. 106-116, 2005.
[9] S. Janssens, Modeling of heat and mass transfer in a areactor for plasma gasification using a hybrid gas-water torch, 2006.
[10] S. Mashayak, CFD modeling of plasma thermal reactor for waste treatment, 2009.
[11] E. Gómez, D. Rani, C. Cheeseman, D. Deegan, M. Wise y A. Boccaccini, «Thermal plasma technology for the treatment of wastes: a critical review,» Journal of Hazardous Materials, vol. 161, nº 2, pp. 614-626, 2009.
[12] H. Huang y L. Tang, «Treatment of organic waste using thermal plasma pyrolysis technology,» Energy Conversion and Management, vol. 48, nº 4, pp. 1331-1337, 2007.
[13] D. Orr y D. Maxwell, «A comparison of gasification and incineration of hazardous wastes,» 2000.
[14] F. Fabry, C. Rehmet, V. Rohani y L. Fulcheri, «Waste gasification by thermal plasma: a review,» Waste and Biomass Valorization, vol. 4, nº 3, pp. 421-439, 2013.
[15] W. Yang, H. Nam y S. Choi, «Improvement of operating conditions in waste incinerators using ingeneering tools,» Waste Management, vol. 27, nº 5, pp. 604-613, 2017.
[16] M. Miltner, A. Makaruk, M. Harasek y A. Friedl, «Computational fluid dynamic simulation of a solid biomass combustor: modelling approaches,» Clean Technologies and Environmental Policy, vol. 10, nº 2, pp. 165-174, 2008.
[17] C. Vega-Sánchez, «I-Plare Reactor 1: Diseño y Simulación de un Reactor para Gasificación por Plasma,» Escuela de Ingeniería Electromecánica. Instituto Tecnológico de Costa Rica, Cartago , 2016.
[18] F. Rojas-Pérez, «I-Plare Reactor 1: Diseño y Simulación de un Reactor para Gasificación por Plasma,» Escuela de Física. Instituto Tecnológico de Costa Rica, Cartago, 2017.
[19] L. Barillas-Mora, «I-Plare Reactor 1: Diseño y Simulación de un Reactor para Gasificación por Plasma,» Escuela de Ingeniería Electromecánica. Instituto Tecnológico de Costa Rica, Cartago, 2016.
[20] D. Wilcox, «Turbulence Modeling for CFD,» DCW Industries, pp. 11-170, 1998.
1 Universidad de Costa Rica. Costa Rica.
Correo electrónico: jose.castillobenavides@ucr.ac.cr https://orcid.org/0000-0001-5177-3482
https://orcid.org/0000-0001-5177-3482
2 Instituto Tecnológico de Costa Rica. Costa Rica.
Correo electrónico: grichmond@tec.ac.cr  https://orcid.org/0000-0001-5147-5952
https://orcid.org/0000-0001-5147-5952
3 Instituto Tecnológico de Costa Rica. Costa Rica.
Correo electrónico: ezamora@tec.ac.cr  https://orcid.org/0000-0002-1753-8291
https://orcid.org/0000-0002-1753-8291
4 Instituto Tecnológico de Costa Rica. Costa Rica.
Correo electrónico: carlosluis111@estudiantec.cr  https://orcid.org/0000-0002-0463-353X
https://orcid.org/0000-0002-0463-353X