Simulación Monte Carlo de un haz de radiación de una fuente de cobalto 60 en condiciones de referencia

Monte Carlo simulation of radiation beam of cobalt 60 source in reference conditions

Walter Vargas-Segura1, Anthony Cordero-Ramírez2

Fecha de recepción: 18 de febrero, 2022
Fecha de aprobación: 6 de julio, 2022

Vargas-Segura, W; Cordero-Ramírez, A. Simulación Monte Carlo de un haz de radiación de una fuente de Cobalto 60 en condiciones de referencia. Tecnología en Marcha. Vol. 36, No 3. Julio-Setiembre, 2023. Pág. 115-126.

https://doi.org/10.18845/tm.v36i3.6137

Palabras clave

Simulación Monte Carlo; Geant4; validación; Cobalto 60; porcentaje de dosis en profundidad; perfil de dosis; radioterapia.

Resumen

El propósito de este estudio es generar la simulación y validación de un haz de cobalto 60 de un equipo de radioterapia en condiciones de referencia, mediante el uso de parámetros de evaluación correspondientes a sistemas de planificación comerciales. Para esto, se utilizaron datos de perfiles de dosis y de porcentaje de dosis en profundidad (PDD) para un tamaño de campo de 10 cm x 10 cm a una distancia fuente superficie (DFS) de 80 cm del maniquí de agua. El programa utilizado para la simulación fue el Geant4, incorporando el haz de radiación, un sistema de colimación y el maniquí. Al comparar los resultados de la simulación con los datos medidos, se obtuvo una diferencia de 3.50 % en la región definida entre el máximo de dosis y el 50 % en la curva de PDD, así como una desviación máxima de 0.96 mm en la zona de acumulación del PDD, además de una desviación de 1.42 mm en la zona de penumbra para el perfil dosis. Para la zona fuera del eje central en el perfil de dosis y en la zona de bajas dosis fueron del 2.41 % y del 2.56 %, respectivamente. Por los resultados obtenidos, se realizó la validación de las condiciones simuladas.

Keywords

Monte Carlo Simulation; Geant4; validation; Cobalt 60; percentage depth dose; perfil dose; radiotherapy.

Abstract

The purpose of this study is to generate the simulation and validation of a cobalt 60 beam of a radiotherapy equipment under reference conditions, using evaluation parameters corresponding to commercial planning systems. For this, we used dose profile and percentage depth dose (PDD) data for a field size of 10 cm x 10 cm at a surface source distance (DFS) of 80 cm from the water phantom. The program used to simulate the radiation beam was Geant4, including a collimation system and the phantom. When comparing the simulation results with the measured data, a difference of 3.50 % was obtained in the region defined between the maximum dose and 50 % in the PDD curve, as well as a maximum deviation of 0.96 mm in buildup region in the PDD. In addition, there is a deviation of 1.42 mm in the penumbra region for the dose profile. For the zone outside the central axis in the dose profile and in the zone of low doses, they were 2.41 % and 2.56 %, respectively. Based on the results obtained, this paper validates the simulated conditions.

Introducción

El uso de programas de simulación que permiten la determinación de la distribución de dosis en diferentes materiales, son utilizados ampliamente en clínica e investigación en diferentes ámbitos de trabajo como radiodiagnóstico, medicina nuclear, radioterapia y protección radiológica [1].

Geant4 es uno de estos programas, el cual ha sido desarrollado en el CERN y cuenta con una amplia comunidad a nivel mundial que contribuyen en su mejora constante [2], [3]. Este ambiente de simulación trabaja mediante el lenguaje de programación C++ y puede ser instalado en diversos sistemas operativos [4].

Por décadas los equipos de teleterapia que utilizan fuentes de cobalto 60 han contribuido a la lucha contra el cáncer [5], hay países que aun utilizan estos equipos, incorporándoles mejoras tecnológicas como un colimador multiláminas [6], [7], que les permitan brindar otros tipos de tratamiento como Radioterapia de Intensidad Modulada (IMRT) [8]. En la actualidad, Costa Rica ya no cuenta con este tipo de equipos, pero se cuenta con los datos dosimétricos de unidades que fueron utilizadas en clínica por muchos años. El haz de radiación generado por un haz de cobalto 60, tiene parámetros dosimétricos bien establecidos y reportados [9]. Por lo que, al ser las fuentes cobalto ampliamente estudiadas resulta de gran valor utilizar este tipo de fuente para el ajuste del ambiente de simulación, y delimitar la forma en que se determinará la dosis y a la vez analizar las capacidades computacionales con que se cuenta, previo a la aplicación de esta técnica en otros equipos emisores.

El propósito de este estudio es la simulación Monte Carlo de un haz de radiación generado por una fuente de cobalto 60 de un equipo de teleterapia utilizando el programa Geant4 para su validación con datos dosimétricos en condiciones de referencia.

Materiales y métodos

Parámetros del haz de radiación

Los datos consultados para este trabajo correspondieron a un haz de radiación de una fuente de cobalto 60 que había sido instalada en un equipo de radioterapia de la marca Theratron 780, con una tasa de dosis aproximada de 368.3 cGy/min en el momento de la medición de los datos dosimétricos, lo cuales fueron el porcentaje de dosis en profundidad (PDD) y los perfiles de dosis en el plano XY, para un tamaño de campo de 10 cm x 10 cm. En el registro se indica que se utilizó un maniquí de agua de dimensiones de 40 cm x 40 cm x 40 cm de la marca PTW colocado a una distancia fuente superficie (DFS) de 80 cm y una cámara de ionización tipo Semiflex de 0.125 cm3 de la marca PTW, colocada a 5 cm de profundidad para la medida de los perfiles de dosis.

Simulación

Para este estudio se utilizó una computadora de escritorio de la marca DELL, con un procesador INTEL CORE i7, el ambiente de simulación utilizado en este trabajo fue el programa Geant4 10.7, instalado en el sistema operativo Ubuntu 20.04. No se simuló la fuente radiactiva de Co-60, ni el cabezal del equipo. Lo simulado fue un haz de radiación, de forma plana y circular de 0.5 cm de radio, considerando una apertura máxima del haz de 5° y con las características energéticas para este tipo de fuente radiactiva. Para fines ilustrativos y visualizar la posición del lugar en que se generó el haz de radiación, en la figura 1 aparece un pequeño cilindro cuyo material no interviene en el proceso de simulación.

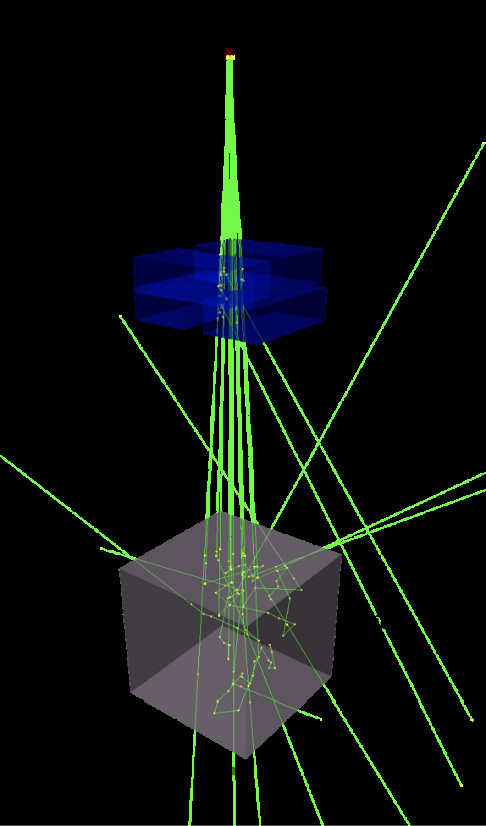
Figura 1. Ilustración de las condiciones de simulación. Las líneas verdes son los rayos gamma generados y dispersados.

Para definir el tamaño de campo se generó en el programa un sistema de colimación que consiste en 4 láminas de plomo de 5 cm de espesor, por 8 cm de ancho y 20 cm de largo. Las láminas que definen el tamaño de campo en la coordenada X, fueron colocadas a 32.5 cm de la fuente y para las láminas de la coordenada Y, fueron colocadas a una distancia de 27.5 cm de la fuente. La posición de las láminas fue modificada para la proyección de un tamaño de campo de (10 x 10) cm2 a un DFS de 80 cm sobre un maniquí de agua de dimensiones de 30 cm x 30 cm x 30 cm, donde la diferencia en dimensiones respecto al maniquí utilizado en mediciones no es significativa [10] (ver figura 1).

Para verificar el PDD en la simulación, se generó un volumen con las dimensiones de 1 mm x 1 mm x 175 mm, el cual está dividido en segmentos de 1 mm x 1 mm x 1 mm y desplazados para que el centro del primer segmento se encuentre a 1 mm de profundidad. Para el caso del perfil de dosis, se generó un volumen con dimensiones de 20 cm x 20 cm x 0.1 cm dividido en segmentos de 1 mm x 1 mm x 1 mm, colocados a 5 cm de la superficie del maniquí, la cual coincide con la profundidad en que se midieron los perfiles de dosis en el equipo. Y sobre la superficie del maniquí se crea un área con dimensiones de 10 cm x 10 cm en que se contabiliza la fluencia de fotones para obtener el espectro de energía.

Para esta simulación se utilizó en el PhysicsList la biblioteca G4Penelope para la interacción del haz de radiación con la materia y una cantidad de 6.0x109 eventos (para obtener el PDD y los perfiles de dosis, en el caso del espectro de energía se generaron 1.0x109 eventos). Este paquete fue desarrollado específicamente para simulación Monte Carlo, el cual proporciona resultados confiables para energías que van desde algunos cientos de eV hasta 1 GeV [11].

Análisis de los datos de simulación

J. Venselaar et al. [12] establece una serie de pruebas para comparar datos dosimétricos medidos con los calculados en los sistemas de planificación comerciales, lo cual corresponde a una metodología para su cálculo, límite de confianza y tolerancias. Basado en esta metodología, los resultados de la simulación, fueron comparados con los datos medidos con el maniquí de agua por la cámara de ionización. Además de la validación, el fin es establecer los alcances de la simulación al ser evaluada con estos criterios, considerándolos parámetros máximos alcanzables. El cuadro 1 resume la información separada en regiones, su descripción y la tolerancia en la evaluación de cada una.

Cuadro 1. Parámetros y tolerancias para la evaluación de PDD y perfiles. [12]

Región	Descripción	Campo homogéneo de geometría simple
d1	Datos sobre el eje central del campo de radiación para la curva de PDD. Zona de alta dosis y de pequeño gradiente de dosis, hasta el 50 % dosis.	2 %
d2	Zona de acumulación en el eje central del campo de radiación en curva de PDD. En la región de penumbra del perfil de dosis, zona de alta dosis y alto gradiente de dosis (región comprendida del 80 % al 20 % del perfil de dosis).	2 mm o 10 %
d3	Zona fuera del eje central del campo de radiación, zona de alta dosis y pequeño gradiente de dosis, hasta el 90 % del perfil de dosis.	3 %
d4	Zona fuera del haz de radiación, de baja dosis y bajo gradiente de dosis, por debajo del 7 % en el perfil de dosis.	3 % (30 %*)

*El autor propone una tolerancia del 30 % si se utiliza la ecuación 1.

La figura 2 muestra los rangos en que son aplicados y evaluados cada uno de los d, al ser comparadas las curvas de PDD y perfiles.

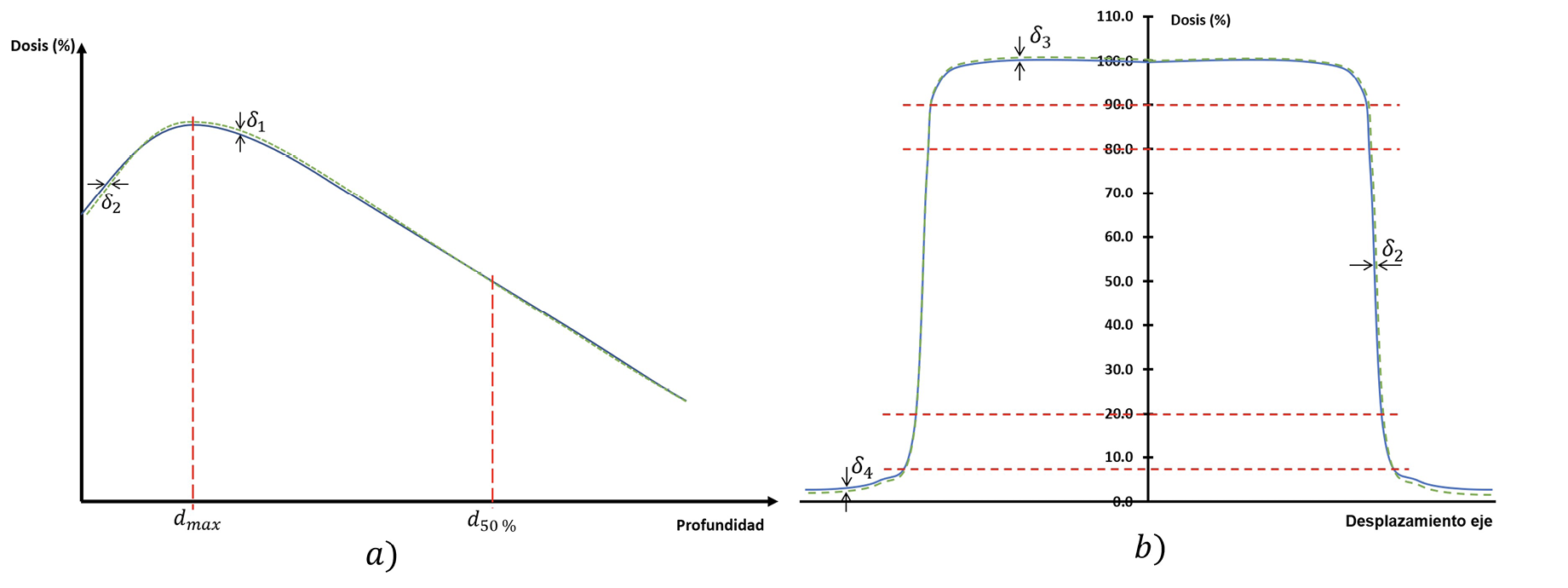
Figura 2. Regiones en que son comparadas las curvas, a) PDD y b) perfil de dosis. Las líneas punteadas delimitan el rango de cada región. Fuente [12]

Los porcentajes para las regiones d1 y d3, fueron calculados mediante la ecuación:

(1)

Dcalc es la dosis obtenida de la simulación y Dmed es resultado de la medida con cámara de ionización. Para el caso de d4 el cálculo fue realizado mediante la ecuación:

(2)

Para la ecuación 2, Dmed,cax es la medida de la dosis en el centro del tamaño de campo. Para el caso de d2, este parámetro trata de medir la variación de la posición de la curva de isodosis de determinado porcentaje que se encuentre en esta región. Para este estudio se determinó la máxima variación de las curvas de isodosis del 20 % al 80 %, en pasos de 10 % para los perfiles de dosis; la zona demarcada por estos porcentajes define la penumbra del campo de radiación [13] y para el caso del PDD, la comparación se realizó con los porcentajes obtenidos a las profundidades de 0.1 cm a 0.4 cm, tomando como referencia la curva medida con la cámara de ionización.

Finalmente, J. Venselaar et al., hace referencia al trabajo realizado por Welleweerd y van der Zee W. [14], que introducen una cantidad llamada límite de confianza, como una medida de la evaluación de las pruebas (d1, d2, d3), el cual se basa en la determinación de la desviación media entre el cálculo y la medición para un número de puntos de datos en situaciones comparables y a una desviación estándar (SD) de la diferencia. Esta cantidad fue calcula mediante la ecuación:

(3)

Aquí se asume una distribución gaussiana de las diferencias entre los valores de dosis calculadas y medidas, siendo el límite de confianza el que determine de manera global si hay o no diferencia. Además, recomiendan el uso del factor de 1.5 en lugar de 1.96. Este valor fue determinado de forma arbitraria y corresponde a una probabilidad P = 0.065, valor el cual ha sido descrito por varios autores como un valor útil en la práctica clínica [14], [15]. Para la valoración global de las regiones se toman las tolerancias indicadas en el cuadro 1.

Resultados

La figura 3 muestra la distribución energética obtenida en la superficie del maniquí simulado, en el que se puede apreciar los dos picos característicos de la energía de los fotones emitidos por el estado exitado del Níquel 60, que es parte de los productos del proceso de decaimiento de los núcleos de Cobalto 60. En la simulación se consideró, la generación de un fotón por evento en la fuente, también fue considerada la probabilidad de emisión, que es ligeramente mayor para los fotones con energía de 1.33 MeV, presentado en su esquema de desintegración [16].

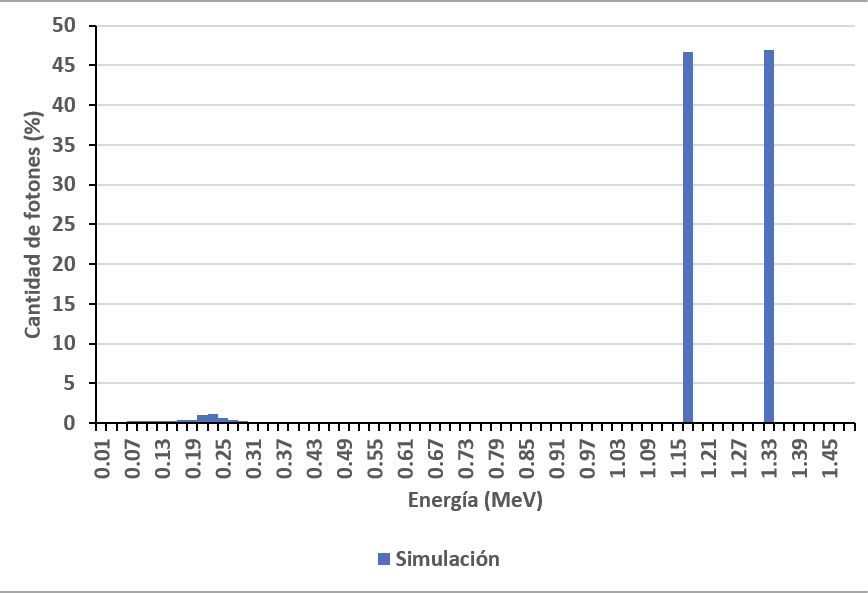
Figura 3. Espectro de energía obtenido en la superficie del maniquí de agua.

La figura 4.a, presenta el espectro mostrado en figura 3 con escala logarítmica en el eje Y para una mejor visualización del porcentaje de fotones contabilizados. En la figura 4.b se observa la contribución de fotones en el espectro de energía por la presencia del maniquí y del colimador.

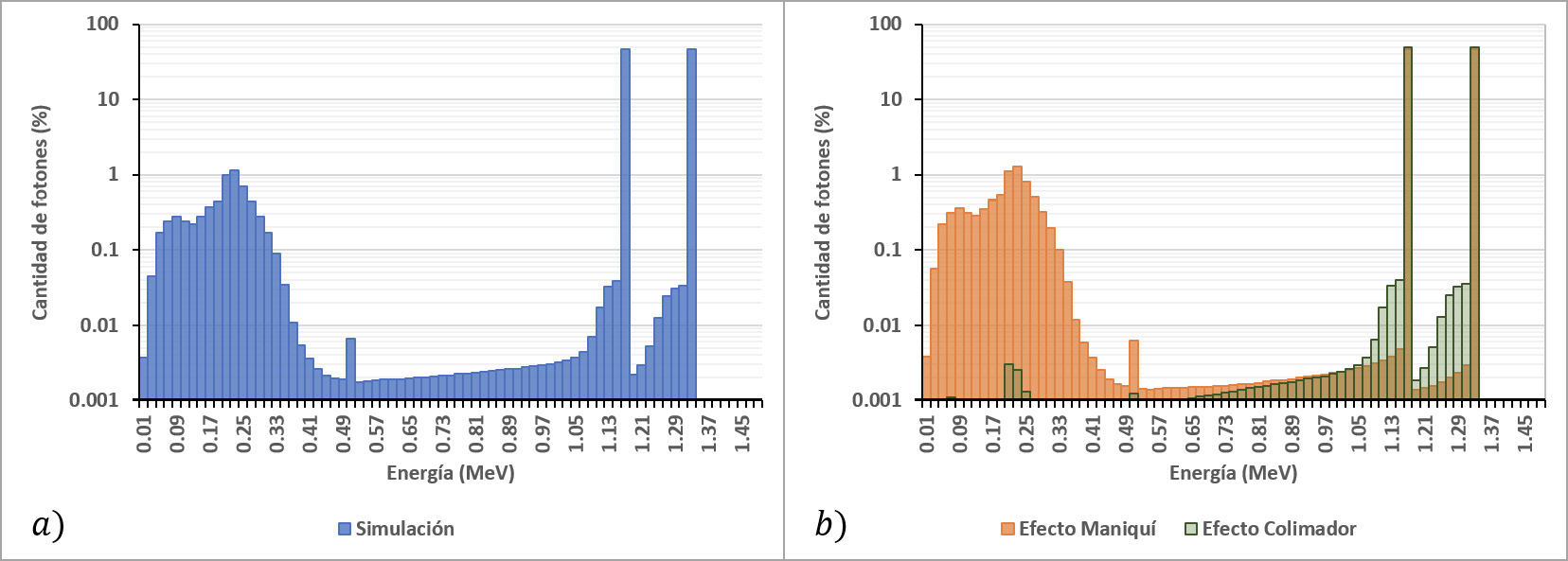
Figura 4. Espectro de energía con escala logarítmica en el eje Y, a) Resultado de la simulación y b) influencia de los componentes simulados.

La figura 5a muestra el PDD obtenido en la medida con cámara de ionización y lo obtenido del proceso de simulación, en ambos casos los datos fueron normalizados al valor de máxima dosis. En la figura 5b se presentan los resultados de la comparación de los datos simulados con los medidos en la región d1, donde las líneas rojas delimitan en la gráfica la zona de ± 2%. En la figura 6 se presenta las variaciones en la posición de las curvas de isodosis en la zona de acumulación (d2). La máxima desviación encontrada de la curva de isodosis en la zona de acumulación fue de 0.96 mm a la profundidad de 1.0 mm, encontrándose dentro de tolerancia.

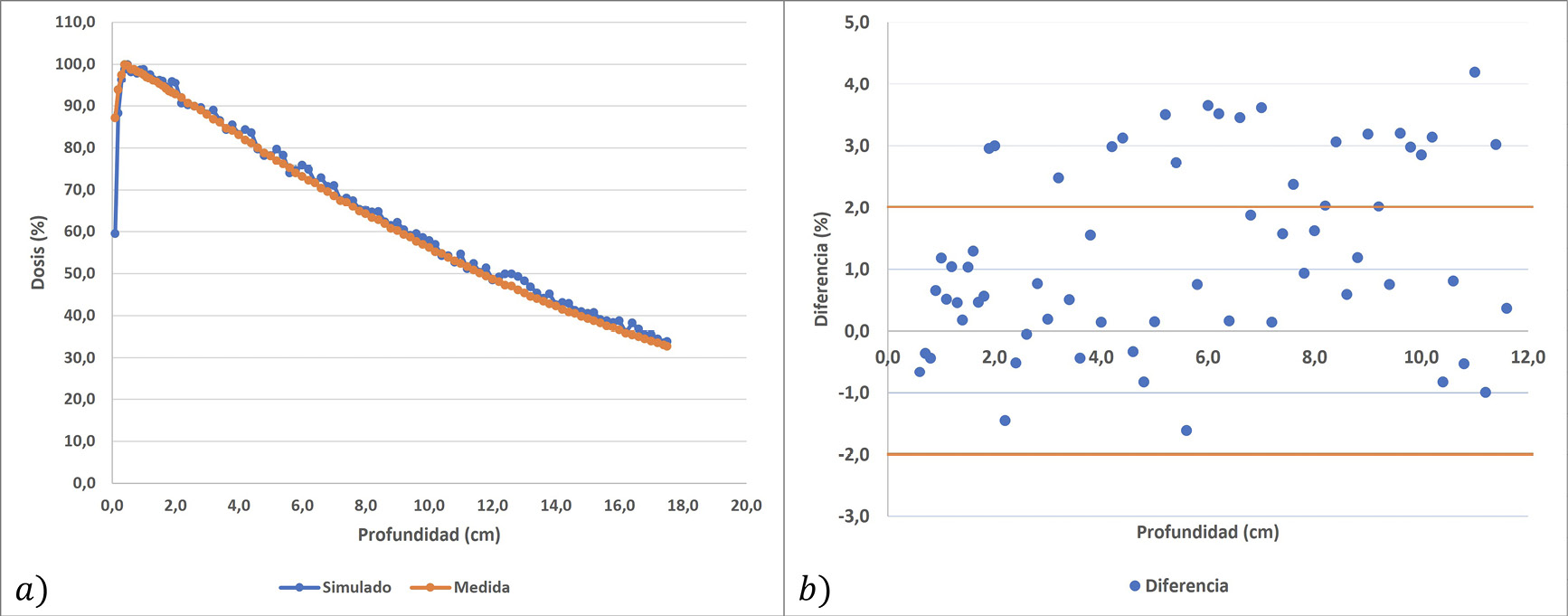
Figura 5. a) PDD simulado y medido. b) diferencia porcentual punto a punto entre PDD simulado y medido.

Figura 6. Variación absoluta de la posición de las curvas de isodosis en la región d2, a) en la curva PDD y b) en los perfiles de dosis.

En la figura 7 se muestran los resultados de los perfiles obtenidos, donde se puede apreciar una gran coincidencia entre los datos simulados con los medidos. En más detalle, las figuras 8 y 9 presentan las variaciones de ambos datos en las regiones d3 y d4, respectivamente. El resultado de la evaluación global de las comparaciones realizadas se presenta en el cuadro 2.

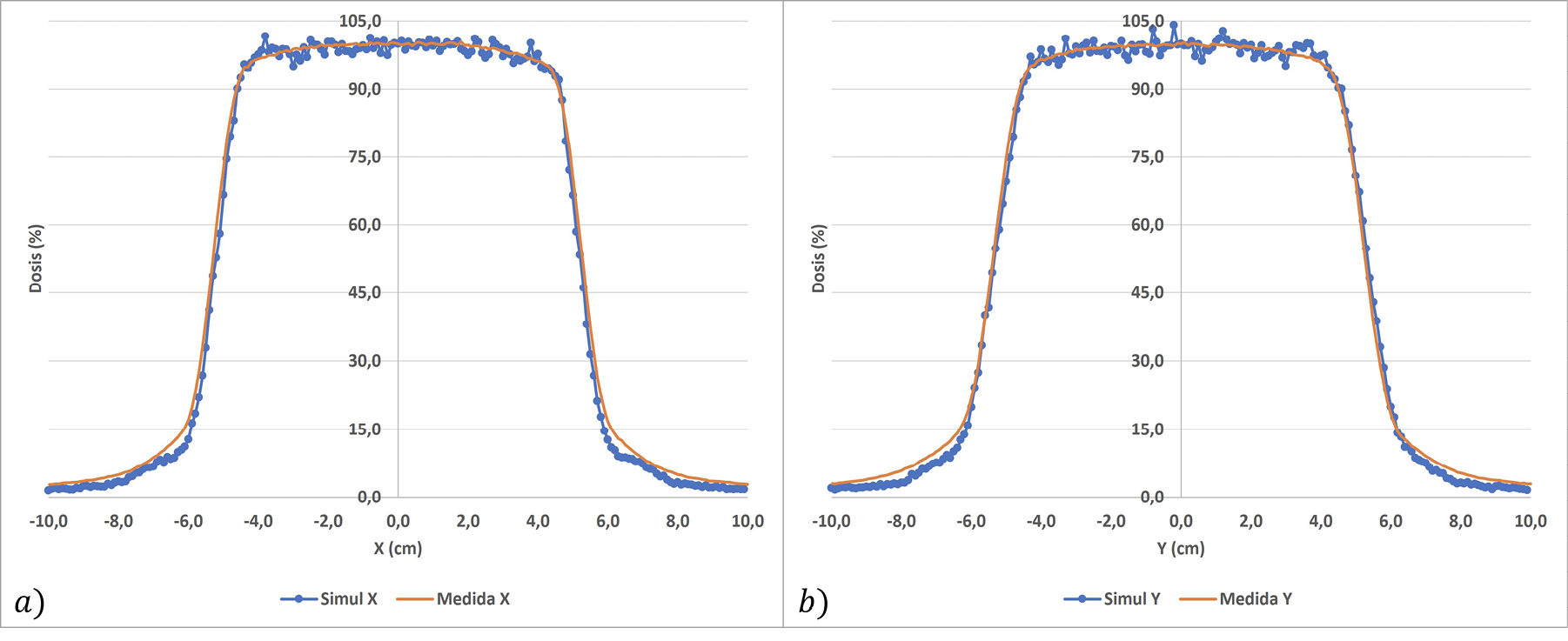
Figura 7. Perfiles de dosis obtenidos del proceso simulación, junto con los valores medidos, a) coordenada X y b) en la coordenada Y.

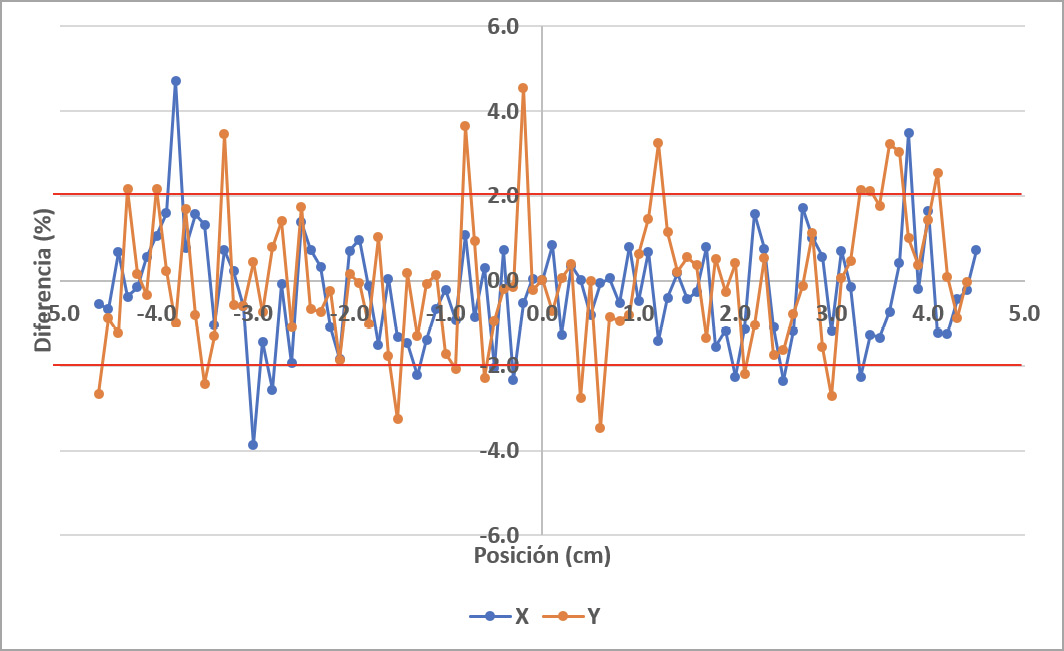
Figura 8. Comparación de los resultados en la región d3.

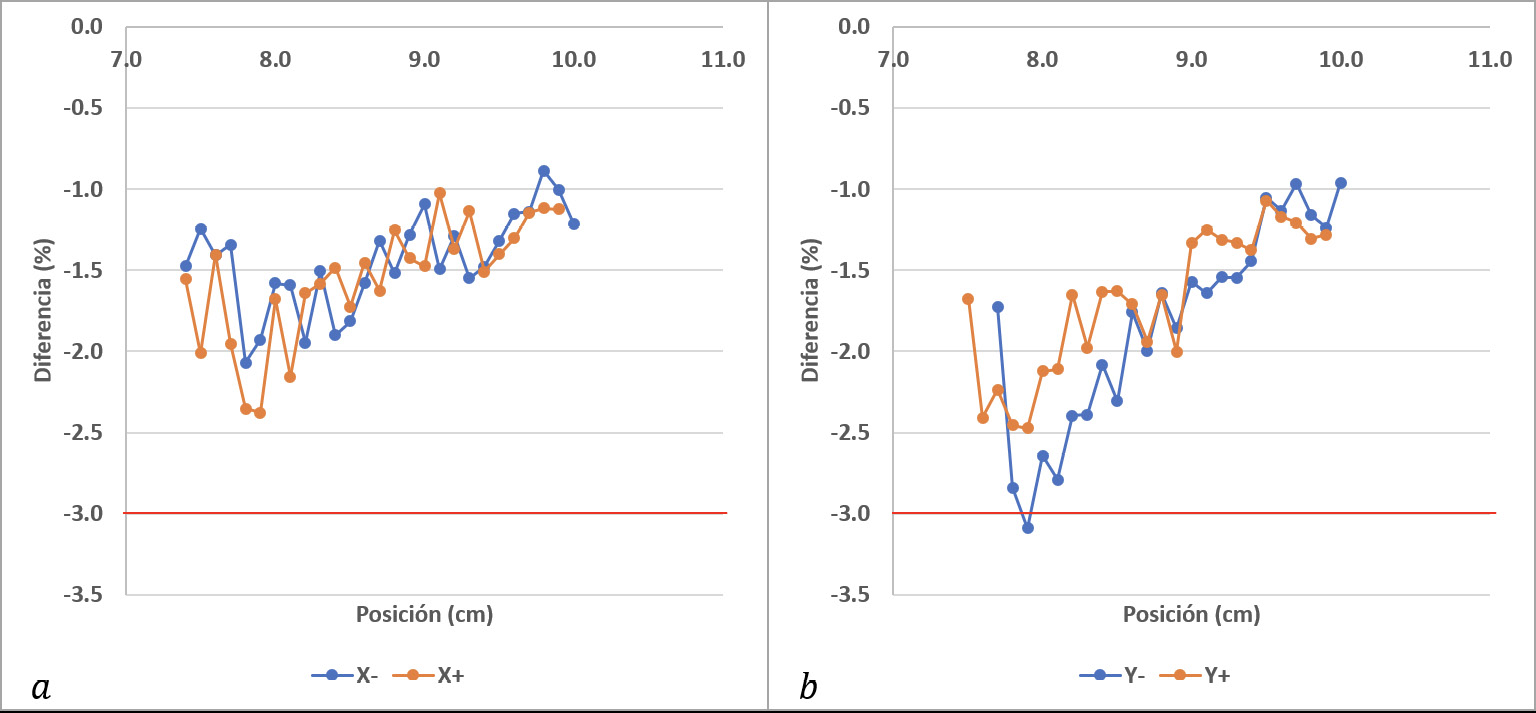
Figura 9. Comparación de los resultados en la región d4, a) en la coordenada X y b) en la coordenada Y.

Cuadro 2. Resultados de los límites de confianza obtenidos en cada región.

Región	Resultado	Tolerancia
d1	3.50 %	2 %
d2	PDD: 0.96 mm	2 mm o 10 %
	Perfiles: 1.40 mm
d3	Coordenada X: 2.20 %	3 %
	Coordenada Y: 2.41 %
d4	Coordenada X: 2.00 % (46.70 %)	3 % (30 %)
	Coordenada Y: 2.56 % (48.93 %)

Discusión

El uso de programas la simulación se convierte en una herramienta muy útil en la determinación de los efectos de los elementos presentes en la distribución de dosis [1]. Para este caso, se estudió la influencia de los elementos simulados (colimador y maniquí) en el espectro de energía. La influencia al incluir en la simulación el blindaje de la fuente radiactiva, el cabezal del equipo y el colimador primario se pueden encontrar en diversos trabajos [17]-[19], en que su contribución se da a bajas energías. Al igual que en esos trabajos, lo mostrado en la figura 4 se aprecia el efecto de retrodispersión del maniquí, mientras que la dispersión generada en el colimador, su influencia se aprecia en las energías cercanas a 1.17 MeV y 1.33 MeV. Además, se puede observar un pico en el rango de 0.5 a 0.52 MeV, el cual es debido a la aniquilación de positrones, generados del proceso de formación de pares, en la interacción del haz de radiación primario sobre el sistema de colimación y el maniquí.

Los resultados obtenidos en la región d1, presentan variaciones importantes (figura 5b) y al calcular el límite de confianza se obtuvo un valor de 3.50 % como resultado global de esta prueba, estando por encima de la tolerancia establecida en el cuadro 1. Esto se debe a que en el proceso de simulación, la medida de la dosis se dio en un medio homogéneo en que el detector de radiación tiene la misma densidad que el maniquí, por lo que no existe perturbación del medio por la presencia del detector [20] y esto es apreciable en la figura 5a, donde la curva de PDD de la simulación presenta valores por encima de los datos medidos en gran parte del intervalo y se confirma con lo mostrado en la figura 5.b en que se aprecia una mayor cantidad de datos en la zona positiva de la gráfica; este resultado es similar al presentado en otros estudios [17]-[19], confirmándose además que la forma y el volumen de la cámara de ionización utilizada en las mediciones influye en el determinación de valores y curva de PDD [21].

Por lo expuesto anteriormente, al trabajar en un medio homogéneo en que no se toma en cuenta el material y movimiento de la cámara de ionización en el ambiente de simulación, se presenta un error sistemático en el resultado del PDD, aunque se obtuvo una diferencia por debajo del 5 % con la cantidad de eventos simulados. De forma similar sucede en la zona de acumulación (d2), y es más evidente a profundidades cercanas a la superficie, en que se obtuvieron valores de porcentaje de dosis a la profundidad de un 1,0 mm de 87.11 % para la medida con cámara de ionización y del 59.40 % en el resultado de la simulación. Esto es corroborado por L. Apipunyasopon et al. [22] que en su estudio comparativo demuestra que la forma y el volumen de diversas cámaras de ionización, influyen en la medida de PDD en la zona de acumulación. Por lo que, al no tener iguales condiciones en la determinación de la distribución de la dosis, se opta por utilizar como parámetro de tolerancia, la desviación en la posición de la curva de isodosis expresada en milímetros, en lugar del porcentaje de la diferencia.

Para el caso de los perfiles de dosis se obtuvieron resultados dentro de las tolerancias presentadas en el cuadro 1. En la región de bajas dosis y bajo gradiente de dosis (d4) al utilizar la ecuación 1 se presentaron grandes diferencias entre las curvas simuladas respecto a las medidas, esto se debe a que es una zona fuera del campo de radiación, en que las partículas cargadas generadas por la radiación dispersa son quienes depositan la dosis [23], factor que no se toma en cuenta en la simulación. Como se mencionó al analizar el espectro de energía obtenido, existen diferentes factores que producen esta radiación dispersa: el maniquí, la radiación de fuga en el cabezal y la dispersión generada en el sistema de colimación. Los resultados obtenidos se deben a que no se simuló el cabezal y el colimador primario, por lo tanto, también el sistema de colimación empleado en la simulación contribuye a esta diferencia.

El método empleado para la comparación de los datos simulados con los medidos, permitió replantear los valores de tolerancia en las que se toma en consideración las capacidades computacionales con que se cuentan y las condiciones de simulación: 4.0 %, 2.0 mm, 3.0 % y 3.0 %, para las regiones d1, d2, d3, d4, respectivamente. Para el caso de d4, solo utilizando la ecuación 2.

Conclusión

Al utilizar en el presente estudio una unidad de cobalto 60 y el uso de criterios de aceptación utilizados en el comisionamiento de sistemas de planificación de tratamiento comerciales, se tiene las suficientes evidencias para delimitar las condiciones del proceso de simulación con el fin de validarlo y aplicarlo en un posterior trabajo en la determinación de dosis absorbida con variadas condiciones física.

Referencias

[1] D. W. O. Rogers. “Fifty years of Monte Carlo simulation for medical physics”, Phys. Med. Biol., Vol. 51, pp: R287-R301, 2006. DOI:10.1088/0031-9155/51/13/R17

[2] Geant4 Collaboration (2020, December 4). Toolkit Developers Guide [Online]. Available: http://cern.ch/geant4

[3] J. Allison et al. “Recent development in Geant4”, Nuclear Instruments and Methods in Physics Research A, 835, pp: 186-225, 2016. http://dx.doi.org/10.1016/j.nima.2016.06.125

[4] Geant4 Collaboration (2020, December 4). Installation Guide [Online]. Available: http://cern.ch/geant4

[5] J. Van Dyk et al. “A retrospective of cobalt-60 radiation therapy: the atom bomb that saves lives”, Medical Physics International Journal, 4, pp: 327-350, 2020.

[6] G. Sri Krishna et al. “DVH Analysis of Cobalt-60 treatment plans incorporating a recently developed MLC”, Int J Cancer Ther Oncol, 4(3):431, 2016. DOI: 10.14319/ijcto.43.1

[7] K. M. Ayyangar et al. “Monte Carlo study of MLC fields for cobalt therapy machine”, Journal of Medical Physics, vol. 39, n° 2, pp: 71-84, 2014.

[8] M. Mathuthu et al. “Dosimetric evaluation of cobalt-60 teletherapy in advanced radiation oncology”, Journal of Radiotherapy in Practice, Vol. 18, pp: 88-92, 2019. DOI: 10.1017/S1460396918000390

[9] M. Cohen. “Central axis Depth dose data for use in radiotherapy. General introduction”, Br. J. Radiol., 11: Suppl 11, pp: 8-11, 1972.

[10] IAEA. “Absorbed Dose Determination in External Beam Radiotherapy. An International Code of Practice for Dosimetry Based on Standards of Absorbed Dose to Water”, Technical Reports Series No.398. Vienna, 2000.

[11] Geant4 Collaboration (2020, December 4). Guide for Physics Lists [Online]. Available: http://cern.ch/geant4

[12] J. Vanselaar et al. “Tolerance for the accuracy of photon beam dose calculations of treatment planning systems”, Radiotherapy and Oncology, 60, pp: 191-201, 2001. DOI: 10.1016/s0167-8140(01)00377-2

[13] H. E. Johns and J. R. Cunningham. “The Physics of Radiology”, fourth edition, Springfield, Illinois: Charles C Thomas Publisher, 1983, ch 10, sec 10.13 pp: 369-371.

[14] J. Welleweerd and W. van der Zee. “Dose calculation for asymmetric fields using Plato version 2.01.”, Abstrac in: Proc. Annual ESTRO Meeting, Edinburgh. Radiother Oncol, 48 (suppl. 1): 134, 1998.

[15] J. Vanselaar and J. Welleweerd. “Application of a test package in an intercomparison of the performance of treatment planning systems used in a clinical setting”, Radiother Oncol, 60, pp: 203-213, 2001. DOI: https://doi.org/10.1016/S0167-8140(01)00304-8

[16] H. E. Johns and J. R. Cunningham. “The Physics of Radiology”, fourth edition, Springfield, Illinois: Charles C Thomas Publisher, 1983, ch. 3, sec. 3.08 pp: 81-84.

[17] A. Kajaria et al. “Monte Carlo simulation of Co-60 teletherapy unit and validation of outcome with dosimetric data published in BJR 25”, JBERR, Vol. 2, No. 2, pp: 30-34, 2015.

[18] J. Won Shin et al. “Application of a Geant4 simulation to a 60Co therapy unit”, Journal-Korean Physical Society, Vol. 59, No. 1, pp: 30-34, 2011. DOI: 10.3938/jkps.59.12

[19] R. Miró et al. “MCNP simulation of a Theratron 780 radiotherapy unit”, Radiation Protection Dosimetry, Vol. 116, No. 1-4, pp: 65-68, 2005. Doi:10.1093/rpd/nci125

[20] P. Andreo. “Monte Carlo simulation in radiotherapy dosimetry”, Radiation Oncology, Vol. 13, 2018. https://doi.org/10.1186/s13014-018-1065-3

[21] W. Cruz et al. “Dosimetric comparison of water phantom, ion chamber, and data acquisition modes for LINAC characterization”, Radiation Measurements, Vol. 82, pp: 108-114, 2015. http://dx.doi.org/10.1016/j.radmeas.2015.09.005

[22] L. Apipunyasopon et al. “An investigation of the depth dose in the build-up region, and surface dose for a 6-MV therapeutic photon beam: Monte Carlo simulation and measurements”, Journal of Radiation Research, Vol. 54, pp: 374-382, 2013. DOI: 10.1093/jrr/rrs097

[23] J. M Bordy et al. “Radiotherapy out-of-field dosimetry: Experimental and computational results for photons in a water tank”, Radiation Measurements, Vol. 57, pp: 29-34, 2013. https://doi.org/10.1016/j.radmeas.2013.06.010

---