Uso de regresión de soporte vectorial para el control de espuma metálica

Using support vector regression for metal foam control

Alexis Sanabria-Castro1, Marcela Meneses-Guzmán2, Bruno Chiné-Polito3

Fecha de recepción: 8 de octubre, 2021
Fecha de aprobación: 17 de febrero, 2022

Sanabria-Castro, A., Meneses-Guzmán, M., Chiné-Polito, B. Uso de regresión de soporte vectorial para el control de es puma metálica. Tecnología en Marcha. Vol. 36, No 1. Enero-Marzo, 2023. Pág. 42-53.

https://doi.org/10.18845/tm.v36i1.5891

Palabras clave

Máquinas de soporte vectorial; máquinas de soporte de regresión; monitoreo de perfiles; perfil de densidad; espuma metálica; control estadístico de procesos.

Resumen

El monitoreo de perfiles se enfoca en aquellas variables de proceso o producto que son caracterizadas por una relación funcional de esta variable respecto del tiempo o el espacio. El objetivo de este trabajo es desarrollar una metodología basada en Regresión de Soporte Vectorial, SVR, para el monitoreo de perfiles no lineales, e implementarla a los perfiles de densidad de un material celular, espuma metálica de aluminio. La forma de un perfil en control está asociada a ciertas características mecánicas del producto, por lo que un cambio significativo de su forma seria detectado como un fuera de control por un método de monitoreo diseñado para este fin; si esto sucediera, se puede concluir que las propiedades mecánicas de la espuma son diferentes a las requeridas. La metodología considera el cálculo de curvas percentiles que serán la base para definir los límites de un gráfico de control, la estimación de parámetros del modelo de SVR con un Kernel Gausseano y con la ayuda de validación cruzada; se evalúa el desempeño del gráfico de control establecido apoyados en la técnica de boostrapping. El método propuesto es sencillo de interpretar y práctico. De acuerdo con los resultados, si la forma del perfil de densidad llegara a cambiar más allá de la indicada variabilidad natural del perfil, el método implementado lo detectaría como fuera de control con un error tipo I de 0.341% (ARLreal= 293).

Keywords

Support vector machines; support regression machines; profile monitoring; density profile; metal foam; statistical process control.

Abstract

Profile monitoring focuses on the process or product variables that are characterized by a functional relationship of this variable with respect to time or space. The objective of this research is to develop a methodology based on Support Vector Regression, SVR, for no linear profiles monitoring and implement it to the density profiles of a cellular material, aluminum metal foam. The shape of a profile is associated to certain mechanic characteristics of a product which means that a significant change in the shape would be detected as an out-of-control observation by a monitoring method designed for this purpose; if this happened, it can be concluded that the mechanic properties would be different from those required. The methodology considers the estimation of percentile curves that will be the basis to define the control chart limits, and the estimation of the parameter Cost and Sigma of a SVR model with a Gaussian Kernel with the aid of cross-validation. The performance of the established control chart is evaluated supported by the boostrapping technique. The proposed method is practical and of simple interpretation. According to the results, if the shape of the density profile were to change beyond the shape indicated by the natural variability of the profile, the implemented method would detect it as out-of-control with a type I error of 0.341% (ARLreal = 293).

Introducción

En algunas situaciones, la calidad de un producto o de un proceso se caracteriza mejor por la relación funcional entre una variable de respuesta y una o más variables explicativas; esta relación funcional que se captura y monitorea a lo largo del tiempo se llama “perfil” y la técnica que se utiliza para su análisis es el Monitoreo de Perfiles, área del Análisis Funcional de Datos (FDA) [1] con un enfoque de Control Estadístico de Procesos (SPC). La literatura ofrece una colección de métodos y técnicas que consideran el tratamiento de perfiles lineales, no lineales y técnicas para reducir la dimensionalidad de los datos, [2], [3], [4]; los estudios se basan en modelos de datos paramétricos y no-paramétricos y la dinámica de funcionamiento consiste en monitorear cambios en los parámetros del modelo por medio de gráficos de control [5]. En muchas aplicaciones un modelo de regresión lineal no es suficiente para representar la forma del perfil, encontrando en literatura propuestas de regresión no lineal, modelos mixtos, splines y wavelets y más recientemente algoritmos de minería de datos, como Redes Neuronales, Árboles de decisión y Máquinas de Soporte Vectorial (SVM). Inicialmente, SVM fue un algoritmo desarrollado para ser utilizado como un clasificador [6], evolucionando hacia algoritmos con aplicaciones de clasificación y regresión para una amplia gama de problemas, desempeñándose con gran exactitud, bajo sesgo en presencia de datos atípicos y con la ventaja de que no tiende a sobreajustarse a los datos, [7], [8].

SVM aplicado a modelos de regresión, llamado Support Vector Regression (SVR), ha demostrado tener buen desempeño generalizado, baja sensibilidad a la dimensionalidad, y la obtención de una solución única que evita óptimos locales, [9], [10]. En el monitoreo de perfiles no lineales, [11] utiliza las SVR para diseñar límites de control que se adapten a la forma de los datos, esta metodología monitorea las curvas regularizadas con el modelo definido. Partiendo de esta propuesta, el objetivo de este trabajo es desarrollar una metodología basada en máquinas de soporte de regresión para el monitoreo de perfiles no lineales. La propuesta en general entrega paso a paso un procedimiento de control de perfiles no lineales basado en SVR, y su validación se muestra mediante la aplicación a perfiles de densidad de una espuma metálica.

Para conocer la estructura interna de un material celular se recurre a métodos de ensayo destructivos y no destructivos que permitan la medición de esta estructura interna y la detección de defectos. Las propiedades mecánicas como por ejemplo de tracción, compresión o torsión, están directamente relacionadas a esta estructura interna que viene representada por la forma del perfil de densidad del material. Entonces, lo interesante del control de calidad de un material como este consiste en medir, mediante un método no destructivo su perfil de densidad y comparar su forma contra un perfil de densidad en control o ideal, para determinar si su estructura interna corresponde o no a un material conforme; por tanto, se concluye que sus propiedades mecánicas, si se midieran, estarían dentro de los parámetros establecidos como de un material conforme.

En las siguientes secciones estaremos abordando la teoría que fundamenta el desarrollo del trabajo. La sección Metodología especifica el procedimiento seguido para diseñar el sistema de control de calidad y se describe el caso de estudio; La sección de resultados muestra la implementación de la propuesta paso a paso y su discusión. En las conclusiones se resumen los hallazgos principales de la investigación y se sugieren futuras investigaciones.

Marco teórico

El algoritmo de Máquinas de Soporte Vectorial para regresión estima una función multivariada de valores continuos la cual puede ser representada por la ecuación 1.

f(x) = wTx + b (1)

Donde:

w = Un vector de pesos o magnitud del valor del hiperplano

x = Un vector de variables

b = Vector de sesgo asociado a la función

La generalización de SVM a SVR se logra introduciendo una región insensible alrededor de la función, llamada margen, que incluyen la mayor cantidad de puntos posible, razón por la cual errores menores que este margen no son penalizados, [6]. El objetivo es encontrar el margen más plano, con el apoyo de vectores de soporte, que mejor se aproxima a la función de valores continuos, mientras que balancea la complejidad del modelo y el error de predicción, para esto, se debe minimizar la norma cuadrada del vector de pesos, [8], [12], ecuación 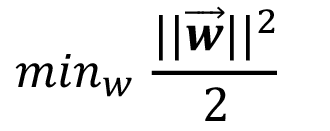2.

(2)

En la Figura 1. vemos que no todos los puntos están dentro del margen, por lo tanto, el problema no es factible, y se debe introducir las variables de holgura 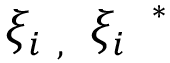. Con esto se obtiene el problema de optimización convexa, ecuación 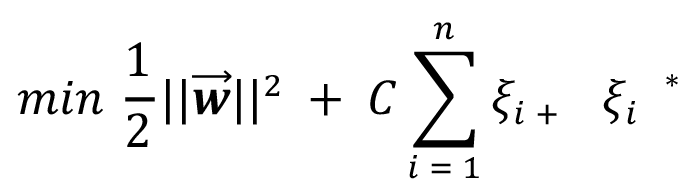3.

(3)

Sujeto a las siguientes restricciones;

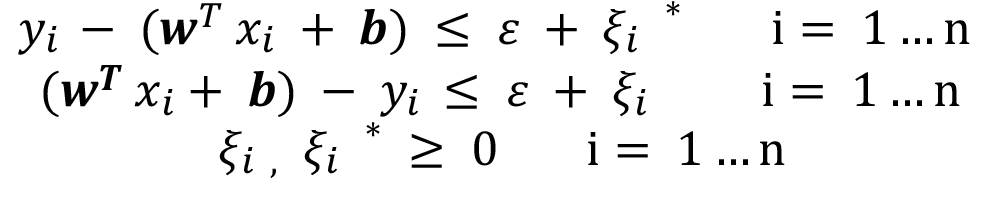
Donde:

yi = Valor real de la variable bajo estudio

wT = Vector de pesos

xi = Valor de la variable de posición

b = Vector de sesgo asociado a la función

C = parámetro de penalización o costo

y = Variables de holgura que determinen cuantos puntos pueden ser tolerados afuera del margen.

ε = Umbral al partir del cual se penaliza el error entre el valor estimado y el valor real

La primera parte de la ecuación (3) maximiza el margen, minimizando la magnitud de los pesos del hiperplano, la segunda parte de la ecuación minimiza el error de entrenamiento. El parámetro C determina el equilibrio entre la regularidad del hiperplano y la cantidad hasta la cual toleramos desviaciones mayores que el margen. Entre mayor es la magnitud del parámetro de costo C, mayor es el interés en minimizar los errores del modelo, mientras que si este tiende a 0, se tendría un número alto de puntos mal representados. Por otro lado, entre menor sea el umbral a partir del que se penaliza el error entre el valor estimado y el valor real, el modelo es menos tolerante con los errores. Este problema de optimización cuadrática se resuelve construyendo una función de Lagrange de la función objetivo y sus restricciones, de esta manera se obtienen los valores 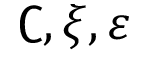óptimos, [8], [12].

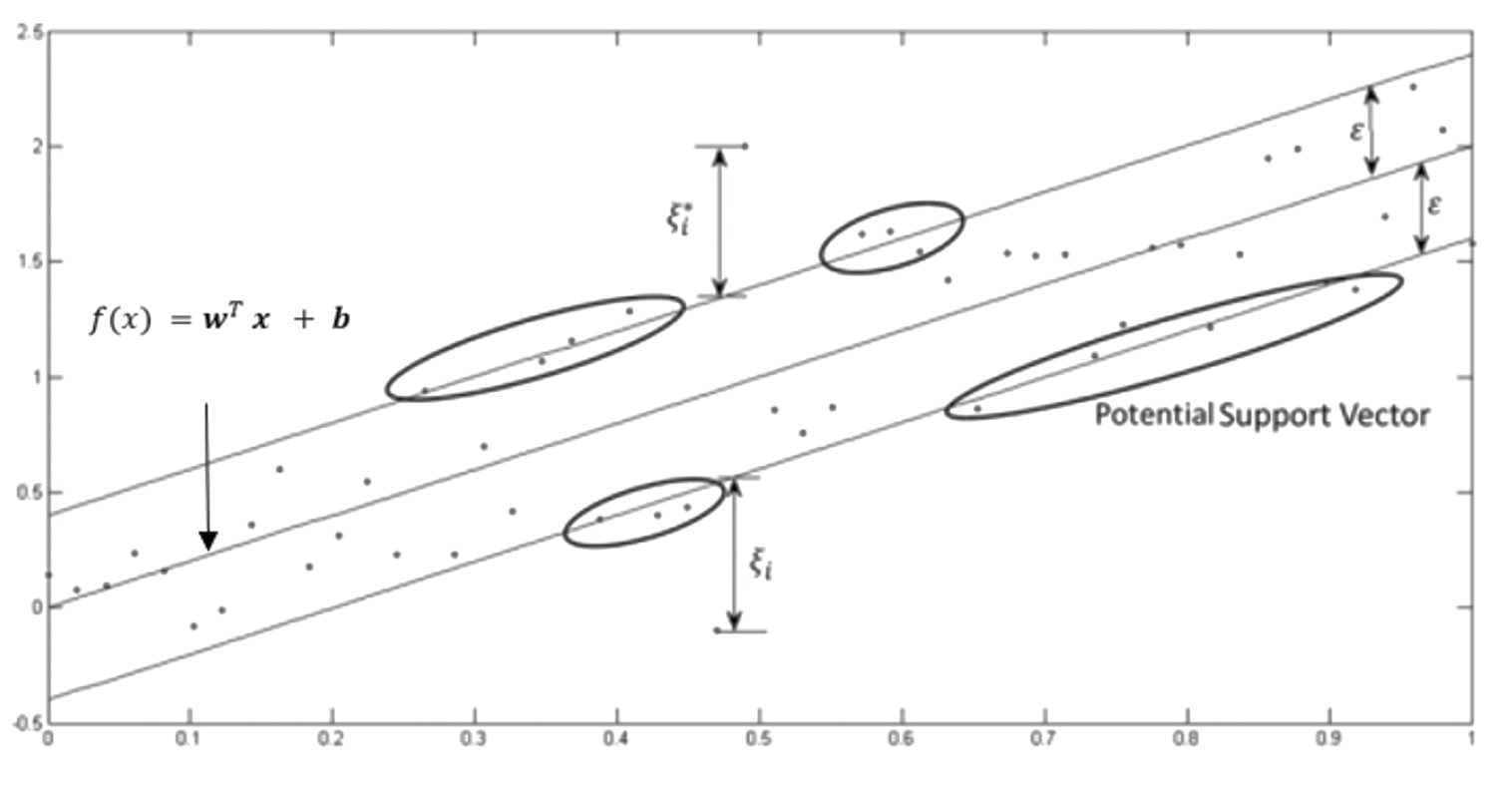
Figura 1. Ejemplo de regresión linear con SVR.

Fuente: Awad et al. 2015

La figura 1 muestra un ejemplo de datos en los que podemos utilizar la función f(x) lineal. Si la relación entre las variables no es lineal, se requiere una transformación de los datos a una dimensión mayor. Esto generalmente se realiza con una función Kernel, la cual convierte relaciones no lineales en lineales; las restricciones para el problema de optimización se establecen de la siguiente manera,

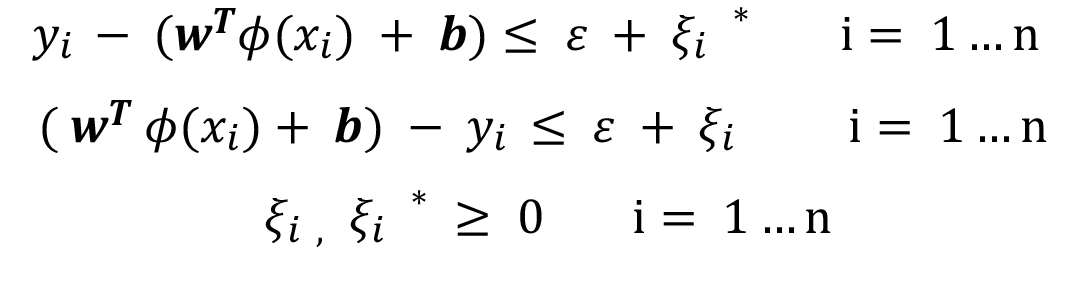
Donde ϕ es la función kernel, una de las más utilizadas es el kernel RBF Gaussiano.

Cuando se está escogiendo un modelo de regresión o clasificación, se debe evaluar y comparar el desempeño de los modelos bajo estudio, normalmente utilizando un set de datos de entrenamiento para definir los parámetros del modelo modelo y otro de prueba para probar el desempeño del modelo, comparando su resultado con la respuesta real. Como la selección de los datos de prueba y entrenamiento podrían proporcionar sesgo en las métricas de desempeño, se suele utilizar alguna técnica de validación como K fold cross validation que utiliza varios conjuntos de datos, los cuales intercalan entre ellos para ser utilizados como conjunto de entrenamiento o de prueba; es usual que en cada una de las iteraciones se registre una métrica de desempeño para obtener al final un promedio de esta, [13].

Bootstrapping es una técnica de estadística inferencial para obtener un estimado de un estadístico de la población. De una muestra bajo estudio se toman muestras aleatorias con remplazo, de las cuales se obtiene una distribución del estadístico de interés, [14], estimando así los parámetros de la distribución, como la media. En este trabajo utilizaremos esta técnica para estimar el número esperado de muestras tomadas antes de que se presente una señal fuera de control o el ARL (average run length), es una métrica para evaluar y comparar métodos de gráficos de control en la fase I o fase de diseño de los gráficos. Dado que se asume que el proceso está en control, entre mayor sea el ARL mejor es el desempeño del gráfico de control. Se calcula como: 1/α, donde α es la probabilidad de que una observación se clasifique como fuera de control, cuando en realidad se encuentra en control estadístico (error tipo I), [15].

Caso de estudio

Una espuma metálica (metal foams) es un sólido celular formado por una red de celdas unidas entre sí formando mallas en su matriz interior, con celdas cerradas, [16]; sus propiedades son la baja densidad y las propiedades típicas de los metales que la componen como lo son, mecánicas, térmicas, eléctricas y acústicas. Las espumas son utilizadas en múltiples aplicaciones con objetivos relacionados a absorción de energía, gestión térmica, aislamiento térmico y acústico y para amortiguamiento mecánico y de vibraciones, entre otras. Las propiedades de los materiales son importantes para definir sus aplicaciones [17] y estas dependen no solo de la composición de la aleación con la cual fue manufacturado, sino que también de la estrategia de producción y las condiciones del proceso. La espuma de aluminio analizada en este trabajo proviene de material espumado de precursores formados por compactación de polvos de aleaciones metálicas con agente espumante (powder compact melting technique), el cual es sometido a calentamiento en hornos de convección en moldes; estas son materiales no homogéneos, caracterizados por la presencia de gradientes de densidad, amplia distribución de dimensiones de celdas y defectos, [18], producto de un proceso aún no completamente dominado y la inestabilidad de producción de espumas con propiedades constantes, [19], [16], [17]. Gracias a que la estructura de las espumas metálicas está relacionada al perfil de densidad del material y que su forma está relacionada a las propiedades mecánicas del material, se tiene el interés de entender esta relación y de definir un método indirecto que contribuya al control de estas propiedades mediante el uso de controles no destructivos.

La muestra de espuma de aluminio 170 – 05, figura 2, es cuadrada con sección 166mm por 40 mm. Para medir la densidad se utilizó la técnica de “gamma scanning” descrita en [20]. Entre otras, se tomaron mediciones de frente X (rayos gamma pasan el espesor Z en dirección X) y frente Y (rayos gamma pasan el espesor Z en dirección Y).

El registro de la intensidad de radiación en diferentes puntos de la pieza permite construir un perfil de intensidad. La densidad del material puede ser determinada por medio de la relación que existe entre esta y la atenuación de los rayos gamma, Ley de Beer – Lambert. En este trabajo usaremos los perfiles de intensidad de radiación de frente X y Y. Se registran 39 perfiles cada 4mm, en cada frente; tres mediciones por cada posición, con periodo de muestreo de 30 segundos por medición. Cada perfil está formado de 82 observaciones separadas cada 2 mm, y registrándolas para las posiciones de 0 mm a 162 mm.

Figura 2. Sistema de referencia para la toma de muestras de la espuma metálica 170 – 05.

Fuente: Bruno et al., 2017

Metodología

Las etapas del análisis y su objetivo fueron desarrolladas con el software R y son:

1.Análisis Exploratorio: Describir los perfiles bajo estudio e identificar y eliminar valores atípicos; estadística descriptiva y visualización.

2.Calcular curvas percentiles que cubra el 99.5% de los perfiles: con los puntos máximos de las mediciones de toda la muestra de perfiles, para cada posición, se determina la curva superior; con los puntos mínimos de las mediciones de toda la muestra de perfiles, para cada posición, se determina la curva inferior. La curva percentil superior e inferior se calcula determinando los percentiles, para cada curva.

3.Selección de parámetro de modelo de SVM: Determinar parámetros de Costo (C) y sigma (σ) para un modelo de SVM con un kernel gaussiano mediante validación cruzada aplicado a la muestra de percentiles superior e inferior. Se obtiene dos pares de parámetros y que son utilizados para regularizar cada percentil superior e inferior y medir cuál de ellos genera un mejor modelo; función tune(svm, ..., tunecontrol = tune.control(cross = 2)).

4.Diseño de límites de control para el monitoreo de perfiles no lineales: Determinar límites de control por medio de la regularización de las curvas percentiles superior e inferior con el modelo SVM seleccionado.

5.Regularización de perfiles muestra: Regularizar por medio del modelo de SVM seleccionado la muestra de perfiles bajo estudio.

6.Identificar curvas fuera de control estadístico: Definir un fuera de control de un perfil mediante la cantidad de puntos de un solo perfil que salen de los límites y utilizar este índice de estabilidad como tolerancia, ej. 10%.

7.Analizar comportamiento de los fuera de control: Determinar si existen patrones de comportamiento de los perfiles fuera de control estadístico por posición, y valores afuera de límites de control.

8.Aplicar 1000 iteraciones de la metodología propuesta a perfiles creados por Bootstrapping, evaluando el desempeño de la propuesta por medio de la métrica ARL.

Resultados y Discusión

Análisis exploratorio

Las figura 3 muestra los 39 perfiles del frente X en azul y los 39 perfiles del frente Y en rojo; la densidad es más alta en los extremos, y progresivamente disminuye hacia la parte central, típica forma de un perfil de densidad de este tipo de materiales; los perfiles X, en general, tiene valores de densidad a lo largo de su comportamiento más bajos que el comportamiento de los perfiles del frente Y; los perfiles del frente Y presentan saltos más pronunciados en las posiciones centrales y hacia la derecha que las que presenta el frente X mostrando picos y valles más pronunciados.

Curvas percentiles

En cada posición en el eje hay 78 observaciones que describen la intensidad de radiación registrada en esa posición y cada una de ellas proviene de un perfil diferente. El punto debajo del que se encuentra un 99.5% de los datos (percentil 99.5%) es el 77.61, redondeado es el punto máximo; el punto debajo del que se encuentra un 0.5% de los datos (percentil 0.5%), es el 0.39, redondeado es el punto mínimo. Se calcula el punto máximo y mínimo en cada posición para construir la curva percentil superior e inferior respectivamente, el conjunto de puntos máximos es la curva percentil superior, y el conjunto de puntos mínimos la curva percentil inferior. La media, el punto máximo y mínimo de la curva percentil 99.5% y 0.5%, superior e inferior son de 1106.7 g/cm3 y 730.1 g/cm3 ;1630.0 g/cm3, y 955.1 g/cm3 ;1011.5 g/cm3 y 624.9 g/cm3 respectivamente.

Figura 3. Perfiles de densidad para las mediciones de frentes X-Y de la espuma metálica 170 – 05.

Selección de modelos de SVR

Utilizando un kernel gaussiano y utilizando valores alternativos de los parámetros costo (C) y sigma (σ) que aumenten de manera exponencial para cada parámetro, y validación cruzada con iteraciones con parámetro de desempeño el error cuadrado promedio (MSE), se determina que el modelo con mejor resultado es de parámetros C = 8 y σ = 16; este modelo se obtiene aplicando el procedimiento a los datos de entrenamiento y es utilizado para regularizar ambas curvas, la de percentiles superior e inferior y que de esta forma pasan a ser los límites de control del gráfico de control. Las curvas percentiles regularizadas con el modelo son representadas en la figura 4 con el color azul. Con estos límites de control, se puede determinar los perfiles que se encuentran fuera de control estadístico.

Aplicación del modelo

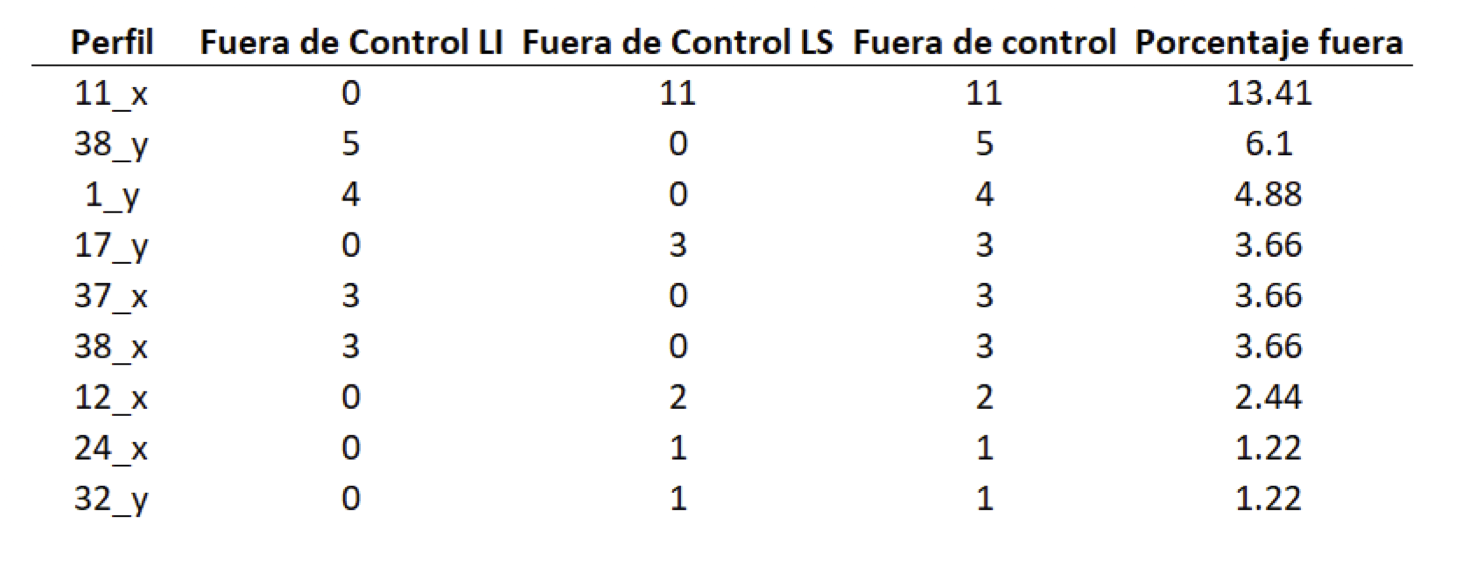
Se aplica un modelo de Máquinas de Soporte Vectorial con sigma de 16 y costo de 8 a cada uno de los 78 perfiles de la muestra, luego se determina si alguno de estos perfiles regularizados tiene puntos fuera de los límites de control. La Figura 4 muestra los 78 perfiles regularizados juntos con los límites superior e inferior del gráfico de control. Se encuentran 9 perfiles fuera de control estadístico (en rojo), cinco son del frente X (55%), perfiles de densidad 11,37,38,12, y 14 y cuatro del frente Y (45%), perfiles de densidad 38,1,17y 32 como muestra la primera columna del cuadro 1.

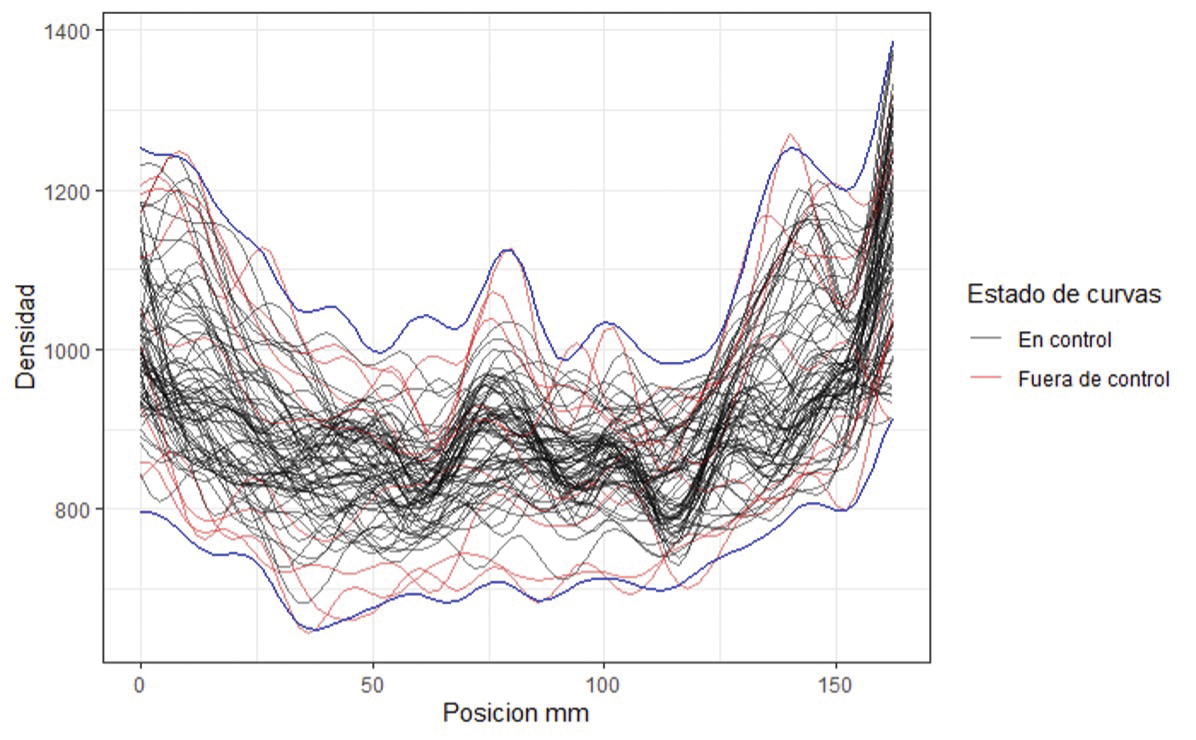
Figura 4. Gráfico de control para los frentes X - Y de la espuma metálica 170 – 05

En las dos siguientes columnas del cuadro se muestra la cantidad de puntos que salen de los límites; de las 33 observaciones fuera de control estadístico, 15 sucedieron en el límite superior (45%), y 18 por el límite inferior (55%). Las 33 observaciones fuera de control estadístico se encuentran distribuidas aleatoriamente a través de la posición. Utilizando como tolerancia para clasificar un perfil fuera de control un índice de inestabilidad mayor al 10%, solamente el perfil 11 en el frente X se encontraría fuera de control estadístico como señala la última columna del cuadro, donde el 100% de las veces que salió de control estadístico fue por el límite superior.

Cuadro 1. Perfiles de densidad fuera de control estadístico para los frentes X-Y de la espuma metálica 170 - 05

Evaluación del desempeño

Se crear 78 perfiles por Bootstrapping, donde cada perfil es el conjunto de puntos promedio en cada posición entre dos perfiles reales muestreados aleatoriamente. A estos perfiles se les aplica el modelo de SVR propuesto y son evaluados en el gráfico de control definido y se cuenta la cantidad de puntos fuera de control estadístico; este proceso se realiza 1000 veces. En promedio, de cada 78 perfiles, 0.266 de los perfiles son clasificados fuera de control estadístico incorrectamente, la cantidad máxima y mínima de perfiles fuera de control estadístico a través de las 1000 iteraciones es de 3 y 0 respectivamente. Por otro lado, asumiendo que cada uno de los perfiles creados está en control estadístico, se calcula la media de esta distribución, y se estima que hay una probabilidad aproximada del 0.341% de clasificar un perfil fuera de control, cuando se encuentra en control estadístico. Por lo tanto, en control estadístico, se espera que cada 293 perfiles (ARLreal), se clasifique un perfil fuera de control incorrectamente.

Conclusiones

Se ha implementado una metodología de monitoreo o control de perfiles no lineales basada en SVR a los perfiles de densidad de una espuma metálica. El modelar el comportamiento de una forma funcional considerada en control, permite determinar un espacio o área de referencia para comparar nuevas mediciones de perfiles limitadas por una curva superior y una curva inferior, que define el espacio dentro del cual una tercera función o perfil podría estar en control si se encuentra dentro de estos límites; si en cambio existieran perfiles de densidad que se salen de estos límites, entonces se clasificaría como un perfil fuera de control y se debería evaluar la gravedad del fuera de control. El método propuesto es sencillo de interpretar, y por lo tanto práctico, y su implementación para el control de perfiles tiene un alcance mayor cuando la forma de este perfil de densidad es asociada a las propiedades mecánicas de la espuma. Si la forma del perfil de densidad llegara a cambiar en forma extraordinaria a los cambios que considera el método implementado, entonces los límites detectarían un fuera de control y se puede asegurar que sus propiedades mecánicas son otras, diferentes a las establecidas. Entonces, los límites de control establecidos para los perfiles de esta espuma, con un nivel alfa de 0.341% (ARLreal = 293), asegurarían que los materiales equivalentes cuyos perfiles de frentes X - Y se encuentren dentro de estos límites, tendrían las propiedades mecánicas que test mecánicos puedan definir para esta muestra.

Los aportes innovadores de esta propuesta están relacionados al cálculo de las curvas percentiles, los cuales son la base para crear los límites de control, y la estrategia de selección de parámetros del modelo de SVR, que es utilizado para regularizar los límites de control y todos los perfiles antes de ser evaluados en el gráfico de control. Futuras investigaciones pueden considerar formas alternativas para definir los límites de control, evaluar el desempeño de la propuesta y comparar esta con otros métodos para comprobar su eficiencia.

Agradecimientos

Los autores agradecen a la Vicerrectoría de Investigación y Extensión del Instituto Tecnológico de Costa Rica, por el apoyo al proyecto 1351022.

Referencia

[1] J. Wang, J. Chiou y H. Muller, “Functional data analysis”, Annual Review of Statistics and Its Application, vol.17, pp. 1- 41, 2015.

[2] W. H. Woodall. “Current research on profile monitoring”, Production, vol.17, pp. 420-425, 2007. https://www.scielo.br/j/prod/a/S6nScq3CJGWnbsCsByxHfJq/?format=pdf&lang=en

[3] L. A. Jones-Farmer, W. H. Woodall, S. H. Steiner y C. W. Champ, “An overview of phase I analysis for process improvement and monitoring”, Journal of Quality Technology, vol.46, pp. 265-280, 2014. https://www.tandfonline.com/doi/abs/10.1080/00224065.2014.11917969

[4] M. Maleki, A. Amiri y P. Castagliola, “An overview on recent profile monitoring papers (2008–2018) based on conceptual classification scheme”, Computers & Industrial Engineering, vol.126, pp. 705-728, 2018. https://doi.org/10.1016/j.cie.2018.10.008

[5] M. Meneses-Guzmán,B. Chiné-Polito, F. Rodríguez-Méndez, V. Mussi, “Characterization of aluminium foams produced via a powder metallurgy route”, Proceedings of the 1st Iberic Conference on Theoretical and Experimental Mechanics and Materials/11th National Congress on Experimental Mechanics, 2017. https://paginas.fe.up.pt/~tem2/Proceedings_TEMM2018/data/papers/7320.pdf

[6] J. Goddard, S. Gerardo, B. Rosa y M. Gutiérrez, “Un algoritmo para el entrenamiento de Máquinas de Soporte para regresión”, Revista de Matemática: Teoría y Aplicaciones, vol.17, p. 107–116, 2000. DOI 10.15517/RMTA.V7I1-2.183

[7] B. Lantz, Machine Learning with R, Packt Publishing, 2013.

[8] M. Awad y R. Khanna, Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers, Springer, pp. 221-232, 2015.

[9] S. Cuentas, R. Peñabaena-Niebles y E. Garcia, “Support vector machine in statistical process monitoring: a methodological and analytical review”, The International Journal of Advanced Manufacturing Technology, vol.91, pp. 485-500, 2017. https://link.springer.com/article/10.1007/s00170-016-9693-y

[10] M. Reis y G. Gins, “Industrial Process Monitoring in the Big Data/Industry 4.0 Era: From Detection, to Diagnosis, to Prognosis”, Processes, vol.5, p. 35, 2017.

[11] J. M. Moguerza, A. Muñoz y S. Psarakis, “Monitoring nonlinear profiles using support vector machines”, de Iberoamerican congress on pattern recognition, Berlin, Heidelberg, 2007. https://link.springer.com/chapter/10.1007/978-3-540-76725-1_60

[12] A. Smola y B. Scholkopf, “A Tutorial on Support Vector Regression”, Statistics and Computing, vol.14, p. 199 – 222, 2004.

[13] P. Refaelizadeh, L. Tang y H. Liu, “Cross – Validation”, Encyclopedia of database systems, vol.5, pp. 532-538, 2009.

[14] G. James, D. Witten, T. Hastie y R. Tibshirani, An Introduction to Statistical Learning with Applications in R, Springer, 2013.

[15] D. Montgomery, Introduction to statistical quality control. John Wiley & Sons, 2020.

[16] J. Banhart, “Manufacture, characterization and application of cellular metals and metal foams”, Progress in Materials Science, vol.46, pp. 559-632, 2001. https://didattica-2000.archived.uniroma2.it//tbs2/deposito/Manufacture,_characterisation_and_application_of_cellular_metals_and_metal_foams.pdf

[17] F. García-Moreno, “Commercial Applications of Metal Foams: Their Properties and Production”, Materials, vol.9, p. 85, 2016.

[18] E. Solorzano, M. A. Rodriguez-Perez, J. A. Reglero y J. A. De Saja, “Density gradients in aluminium foams: characterisation by computed tomography and measurements of the effective thermal conductivity”, Journal of Materials Science, vol.42, pp. 2557-2564, 2007.

[19] C. Körner y R. F. Singer, “Processing of metal foams—challenges and opportunities”, Advanced Engineering Materials, vol.4, pp. 159-165, 2000. https://onlinelibrary.wiley.com/doi/pdf/10.1002/%28SICI%291527-2648%28200004%292%3A4%3C159%3A%3AAID-ADEM159%3E3.0.CO%3B2-O

[20] F. Rodríguez-Mendez, M. Meneses-Guzmán, B. Chiné-Polito, R. Pereira-Arroyo, “Desarrollo de un sistema automatizado de escaneo por radiación gamma”, Tecnología en Marcha, vol. 32, 3, pp 87-98, 2019. https://dialnet.unirioja.es/servlet/articulo?codigo=7448586

---