Comparación de métodos de detección del inicio y término de la estación lluviosa basado en datos de precipitación

Comparison of detection methods for the onset and demise of the rainy season based on precipitation data

Pablo Ureña-Mora1, Eric J. Alfaro2

Ureña-Mora, P; Alfaro, E.J. Comparación de métodos de detección del inicio y término de la estación lluviosa basado en datos de precipitación. Tecnología en Marcha. Vol. 35, No 4. Octubre-Diciembre, 2022. Pág. 124-137.

https://doi.org/10.18845/tm.v35i4.5778

Palabras clave

Inicio y término de la estación lluviosa; América Central; precipitación; variabilidad climática.

Resumen

Diferentes metodologías han sido propuestas para la detección del inicio y término de la estación lluviosa que incluyen el área de América Central. Índices de temperatura superficial del mar, descomposición de valores singulares, mínimos cuadrados, pentadas de precipitación, desviación de la precipitación acumulada, han sido analizados por otros autores. Este estudio compara dos metodologías que utilizan únicamente observaciones de la precipitación, la primera consiste en el análisis de la precipitación acumulada diaria y la segunda consiste en calcular la desviación de la precipitación acumulada (DPA), ambas metodologías sujetas a diferentes criterios de detección. Adicionalmente se propone y se agrega a la comparación una modificación del criterio basado en la DPA. Se analiza el registro diario de 101 estaciones pluviométricas con régimen anual bimodal en América Central desde 1968 al 2012. Se encontró que la metodología basada en DPA detecta falsos inicios de la estación lluviosa (IELL) y alarga la detección del término de la estación lluviosa (TELL). Al compararlo con el método basado en DPA, el criterio propuesto obtuvo un valor similar de tendencia central del IELL, TELL y la duración de la estación lluviosa, además muestra menos variabilidad que los otros dos métodos.

Abstract

Several methodologies have been proposed for the onset and demise dates of the rainy season in the Central American isthmus. Sea surface temperature indices, singular value decomposition, least squares method, precipitation pentads, accumulated precipitation deviation, have been analyzed by other authors. This study compares two methodologies that use only precipitation observations, the first one consists of accumulated daily precipitation analysis and the second computes the accumulated precipitation deviation (APD), both methodologies subject to different detection criteria. Additionally, a modification of the criterion based on the APD is proposed and added to the comparison. A daily set of 101 bimodal annual cycle rain gauge stations in Central America from 1968 to 2012 is used. We found that the APD-based methodology detects false onsets and lengthens the demise of the rainy season. Between the results of the pentad method, the proposed criterion achieves a similar central tendency date of the onset, demise and the duration of the rainy season, in addition it shows less variability than the other two methods.

Keywords

Onset and demise of the rainy season; Central America; precipitation; climate variability.

Introducción

Para calcular el inicio y el término de la época lluviosa se han utilizado numerosas técnicas y diferentes variables meteorológicas. Por ejemplo, Zuo et al. [1] utilizaron patrones predecibles de la precipitación monzónica en el verano del Hemisfério Norte, comparando los modos principales de anomalías de precipitación observada en los monzones y luego los compararon con los del pronóstico actualizado del modelo Climate Forecast System Version 2 [2] encontraron correlaciones significativas con la variabilidad de la temperatura superficial del mar (TSM) del Atlántico y Pacífico tropical. Enfield y Alfaro [3] utilizan dos enfoques independientes para el análisis de las relaciones interoceánicas con la lluvia en América Central. El primero es un análisis de descomposición de valores singulares (DVS), aplicado a conjuntos de datos de rejilla de TSM y precipitación acumulada (PCPA) mensual para detectar diversas configuraciones de la TSM del Pacífico y del Atlántico y sus asociaciones con la precipitación, donde encontraron modos que relacionan la TSM y la PCPA. El segundo, la relación de los índices de TSM con las fechas de inicio de la estación lluviosa (IELL) y término de la estación lluviosa (TELL) en América Central donde uno de sus resultados más importante es la relación que un Atlántico Tropical Norte (ATN) cálido (frío) favorece una expansión (contracción) de la temporada de lluvias en ambos extremos en el sur de América Central.

En la región Mesoamericana, Díaz-Alcántara [4] propone que la actividad convectiva de la Zona de Convergencia Intertropical (ZCIT) induce circulaciones relacionadas con ondas ecuatoriales que llevan humedad y provocan las lluvias. Utiliza datos de un modelo numérico y de estaciones meteorológicas de la costa del Pacífico Mesoamericano, como criterio para el cálculo de la fecha del IELL, realiza pendientes de PCPA utilizando el método de mínimos cuadrados con una ventana de diez días. Para realizar el cálculo de la fecha del IELL usó datos del modelo Global Precipitation Climatology Project 1-Degree Daily Combination 1 [5], y define como el IELL al cambio de pendiente en la PCPA para cada año.

Alfaro et al. [6] utilizaron las distribuciones de la TSM en los océanos Pacífico y Atlántico para explicar las variaciones de las fechas del IELL y el TELL sobre América Central, donde sus resultados muestran correlaciones significativas entre el índice del ATN con el IELL, el Índice de Oscilación del Sur (IOS) con el TELL y el Niño 3 también con el TELL. Alfaro y Cid [6], usaron datos de precipitación pentadal (precipitación acumulada durante 5 días), utilizando una versión modificada de la metodología propuesta por [8]. Por otro lado, Hernández y Fernández [9] relacionan datos de precipitación y evapotranspiración diaria para obtener umbrales del inicio y término de la estación lluviosa utilizando el método FAO Penman-Monteith o FAO-56 de Allen et al. [10]. El método del análisis del inicio y término de la época lluviosa (ITELL) utilizando péntadas de precipitación acumulada también fue utilizado por Nakaegawa et al. [11] en Panamá, y Rivera-Ramos et al. [12] en la zona sur de Guatemala, los últimos con las mismas pentadas aplicaron un segundo criterio que consiste en la diferencia entre el valor promedio anual de precipitación pluvial y el valor de precipitación de cada pentada propuesto por Liebmann y Marengo [13].

En la presente investigación se utilizará un método elaborado para capturar un cambio estacional en el régimen de precipitación en América Central adaptado para ser usado con modelos de pronóstico y análisis retrospectivo. Este método, que solo usa datos de precipitación, fue diseñado por Bombardi y Carvalho [14], basado en el método propuesto por Liebmann y Marengo [13]. El objetivo de este trabajo es comparar dos metodologías para calcular el inicio y término de la estación lluviosa de estaciones meteorológicas con ciclo anual de precipitación bimodal en la región centroamericana [15] utilizando primero el análisis de las péntadas de precipitación diaria acumulada y segundo el cálculo de la desviación de la precipitación acumulada (DPA), ambas metodologías sujetas a diferentes criterios de detección.

Materiales y métodos

Se utilizan datos diarios de precipitación acumulada de 1968 al 2012 de las 101 estaciones mostradas en la figura 1. Estas estaciones en su mayoría son de tipo bimodal con una estación lluviosa y seca muy marcada [15], escogidas según el criterio de Alfaro e Hidalgo [16]. Para tener series de tiempo completas se rellenan los datos con la metodología de rellenado de datos geofísicos expuesta por Alfaro y Soley [17] donde como primera aproximación se usa un rellenado por medio de un filtro predictivo AR(p) y luego utilizando el método de componentes principales [18]. Para estos datos se utilizaron 5 componentes principales.

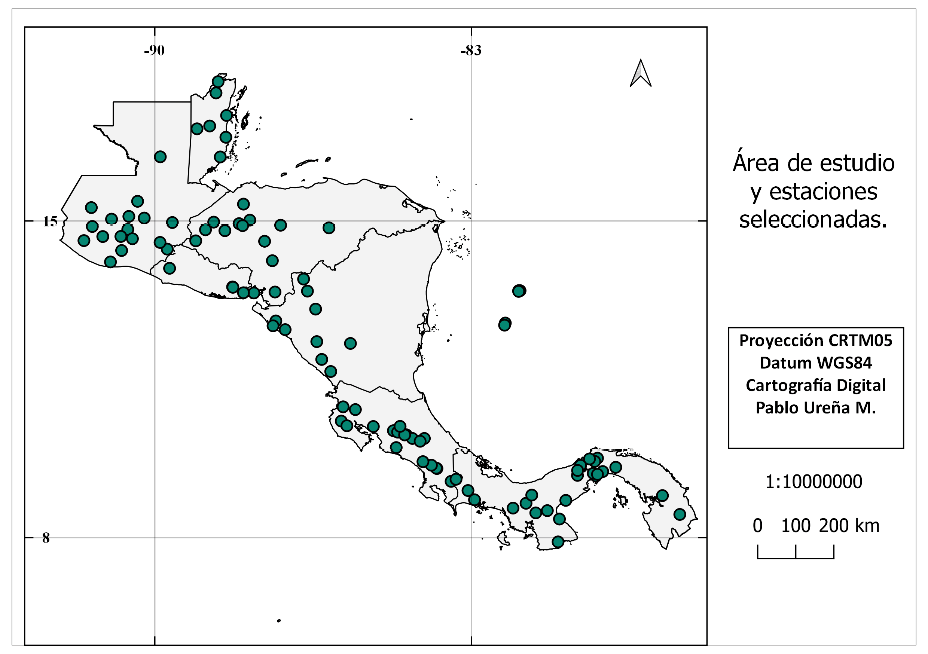
Figura 1. Mapa de la distribución de estaciones utilizadas en América Central.

Cálculo de las fechas de inicio y final de la época lluviosa

Primero, para el análisis de las péntadas de precipitación diaria acumulada, basado en la metodología desarrollada en Alfaro [19], y también aplicada en [16, 20, 21, 22], las series de tiempo de precipitación diaria se filtraron utilizando un promedio móvil de peso triangular con una ventana de 31 días [23], para evitar o minimizar las interrupciones del inicio debido a posibles fortalecimientos de corta duración de los vientos alisios. Se aplicó un algoritmo para identificar sistemáticamente el inicio a la serie de tiempo de precipitación diaria filtrada. La metodología de Gramzow y Henry [14], que fue posteriormente adaptada en [3, 6, 7, 24], consiste en que para un año en particular y en un registro de estación en particular, el inicio de las lluvias (en días julianos) se asocia con aquel día en que la precipitación suavizada es mayor a 5 mm día−1 durante al menos 10 días (o dos pentadas seguidas) y si en los siguientes 5 días (por ejemplo, la siguiente pentada), la precipitación observada es superior a 0.1 mm día−1. El final de la estación lluviosa es calculado de una manera similar invirtiendo la serie e iniciando del último día del año hacia el inicio.

Segundo, para calcular las fechas de inicio y final de la época lluviosa, basado en el cálculo de la desviación de la precipitación acumulada (DPA), se utilizó para cada año la derivada en el tiempo de la desviación de la precipitación acumulada S(n) (1) del promedio n expuesta por Bombardi et al. [25], donde P(i) es la precipitación diaria el día i, PC es el promedio diario anual de la precipitación (razón climatológica de la precipitación) y una variante de esta. La primera utiliza una media móvil triangular de tres valores para suavizar la curva de S(n). Como criterio de selección desde el inicio de cada año, el primer día donde la derivada pasa de valores negativos a positivos es considerado el inicio de la estación lluviosa, y se mantiene mientras los valores positivos persisten durante tres días.

El final de la estación lluviosa es calculado de una manera similar invirtiendo la serie e iniciando del último día del año hacia el inicio.

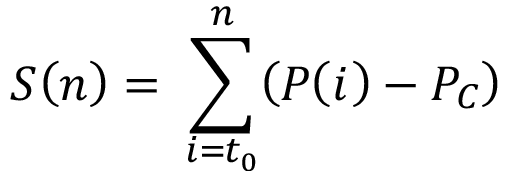(1)

La variante propuesta en este trabajo como tercera opción, utiliza S(n), con la diferencia que para suavizar esta curva se aplica un promedio móvil de peso triangular de treinta y un valores. Además, el criterio de selección del inicio de la estación lluviosa se escoge el primer día donde la derivada pasa de valores negativos a positivos, y se mantiene mientras los valores positivos persisten durante diez días. Para el término de la estación lluviosa se invierte la serie y se aplica la metodología anterior. A este criterio se le llamará Bombardi modificado.

Significancia estadística de las diferencias del promedio

Se calcula la duración de la época lluviosa con la diferencia entre los promedios del TELL y el IELL para el conjunto de datos de Alfaro e Hidalgo [16], la metodología de Bombardi et al. [25] y la variante propuesta en la sección anterior. Se realizan dos pruebas de hipótesis de diferencia de medias utilizando el promedio de los conjuntos de datos, la prueba paramétrica t de dos muestras y la prueba no paramétrica de suma de rangos Wilcoxon [26], entre los datos del IELL, TELL y duración de la época lluviosa (definida como TELL-IELL+1).

Resultados

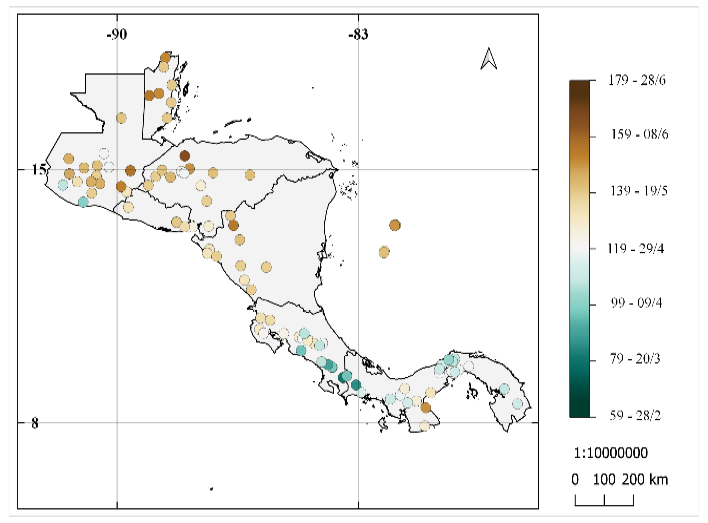
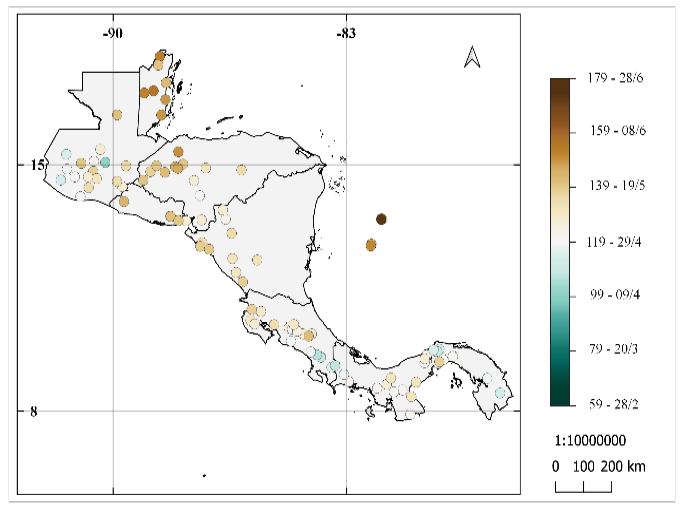
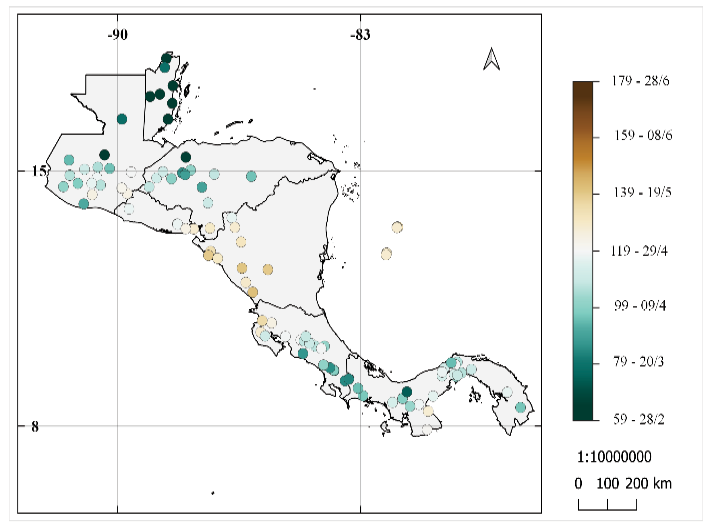
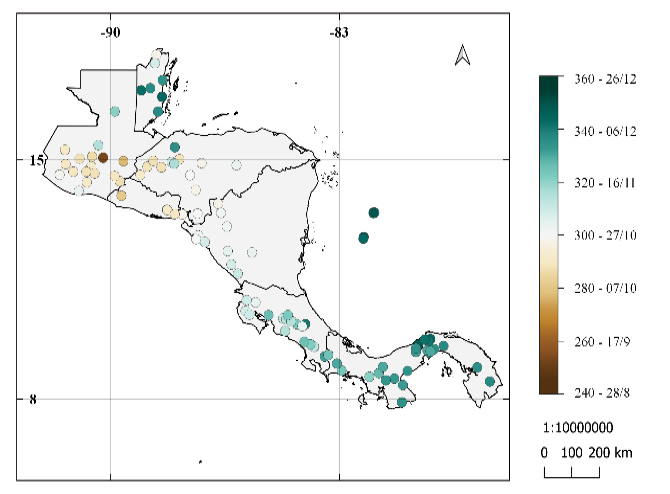
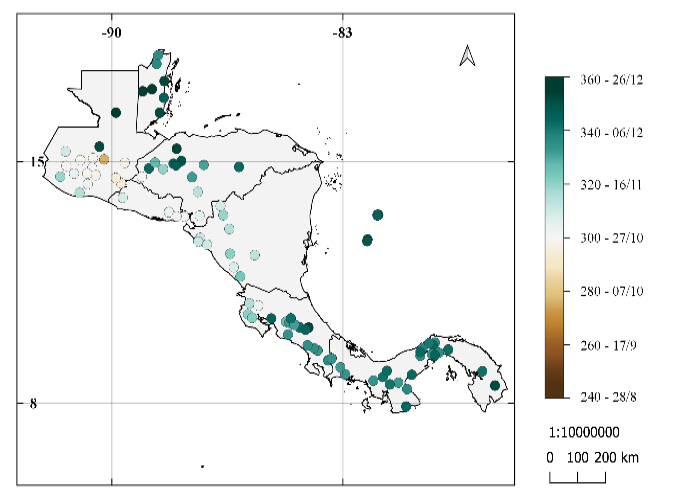
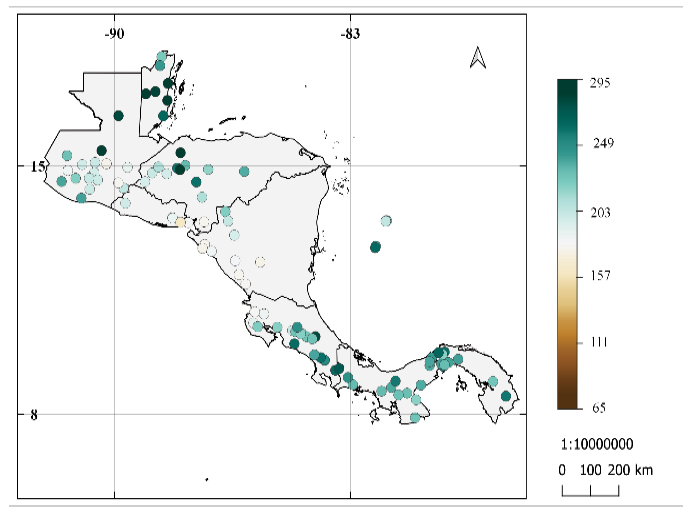
En la figura 2 se muestra el IELL para las estaciones de la figura 1. Se observa que los inicios tempranos de la ELL se dan desde el 28 de febrero y los inicios tardíos hasta el 28 de junio, entre los mapas se pueden notar similitudes y diferencias entre los resultados. La parte norte de América Central tiene inicios más tardíos que la parte sur (Costa Rica, Panamá), excepto el sur de Honduras que tiene inicios tempranos de la ELL. En las tres metodologías hay una estación en la Península de Azuero de Panamá, en la región conocida como el Arco Seco, con inicio más tardío que las de su alrededor, por otro lado, el sur de Costa Rica y este de Panamá tiene el inicio más temprano de toda la región entre los resultados de la metodología de Alfaro e Hidalgo [16] y la metodología propuesta.

Se observa que el criterio de Bombardi en Belice y norte de Guatemala no concuerda con los resultados de Alfaro e Hidalgo [16] y Bombardi modificado, mostrando inicios tempranos cuando en las dos metodologías anteriores muestran inicios tardíos. Para el IELL los datos muestran un rango del inicio desde el 28 de febrero al 28 de junio.

Los diagramas de caja del conjunto de datos de la figura 2 son mostrados en la figura 3. Se observa que los resultados de la metodología de Alfaro e Hidalgo [16] tienen valores atípicos correspondientes a inicios tempranos de la ELL, para esta serie la mediana se da el 13 de mayo, el primer cuartil el 30 de abril y el tercer cuartil el 20 de mayo. Los resultados de la metodología modificada propuesta presenta un valor atípico correspondiente a un inicio tardío de la ELL, y tienen la mediana el 10 de mayo, el primer cuartil el 4 de mayo y el tercer cuartil el 17 de mayo. Los resultados de la metodología propuesta por Bombardi et al. [25] muestran valores atípicos correspondientes a inicios tempranos de la ELL, una mediana el 19 de abril, el primer cuartil el 5 de abril y el tercer cuartil el 28 de abril.

a)	b)
c)

Figura 2. Promedio del número de día juliano y fechas de inicio de la época lluviosa para las 101 estaciones entre 1968 al 2012 utilizando: (a) resultados de la metodología de Alfaro e Hidalgo [25], (b) resultados de la metodología modificada propuesta, (c) resultados de la metodología utilizada por Bombardi et al. [16].

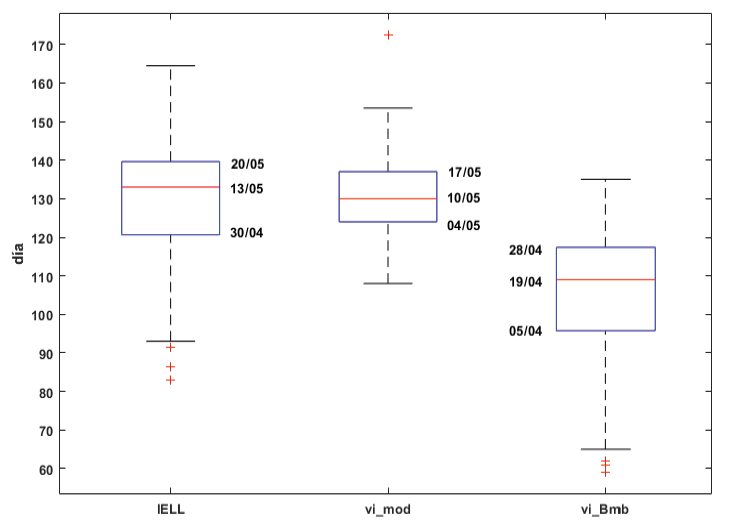
Figura 3. Diagramas de caja del inicio de la ELL para los resultados obtenidos de la figura 2. IELL: resultados de la metodología de Alfaro e Hidalgo [16], vi_mod: resultados de aplicar la metodología modificada propuesta, vi_Bmb: resultados de aplicar la metodología propuesta por Bombardi et al. [25]. Se muestran las fechas del primer cuartil, la mediana y tercer cuartil.

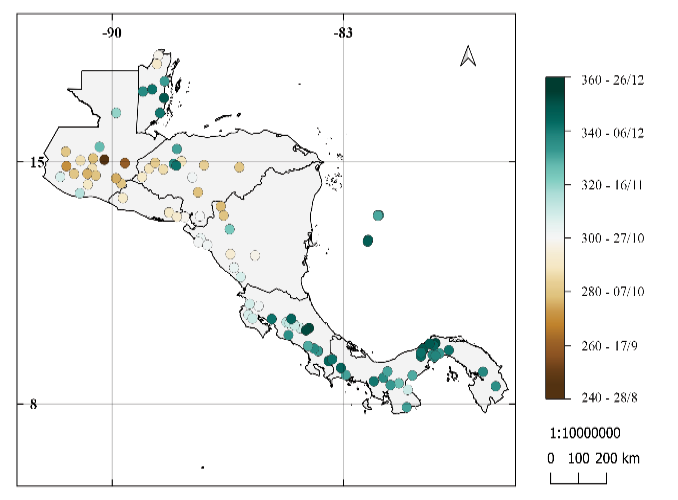
Para el TELL (figura 4) se puede observar a partir de los resultados de las tres metodologías que, del centro de Costa Rica hacia el sur, junto con Providencia y San Andrés, unas estaciones al norte de Honduras, norte de Guatemala y en el centro y este de Belice, se tiene el término de la estación lluviosa más tardío (más colores verdes). Se observa que, en el centro de Costa Rica hacia el norte, la parte central y Pacífico de Nicaragua, Honduras, El Salvador, y Guatemala, se tiene el término de la estación lluviosa más temprano (más colores cafés).

La metodología de Bombardi et al. [25] muestra el final de la estación lluviosa más larga al noroeste de Honduras que en las otras dos metodologías donde lo muestran con final más temprano (tonos más cafés). El rango del término de la estación lluviosa como resultado de los tres criterios aplicados para el conjunto de datos es del 28 de agosto al 26 de diciembre.

Los diagramas de caja para el conjunto de datos de TELL son mostrados en la figura 5. Para estas series no se presentaron valores atípicos. Los resultados de la metodología de Alfaro e Hidalgo [16] muestran la mediana el 13 de noviembre, el primer cuartil el 20 de octubre y el tercer cuartil el 6 de diciembre, los resultados de la metodología modificada muestran la mediana el 9 de noviembre, el primer cuartil el 25 de octubre y el tercer cuartil el 30 de noviembre, por otro lado, los resultados de aplicar la metodología de Bombardi et al. [25] muestran la mediana el 4 de diciembre, el primer cuartil el 10 de noviembre y el tercer cuartil el 12 de diciembre.

a)	b)
c)

Figura 4. Similar a la figura 2 para el término de la época lluviosa.

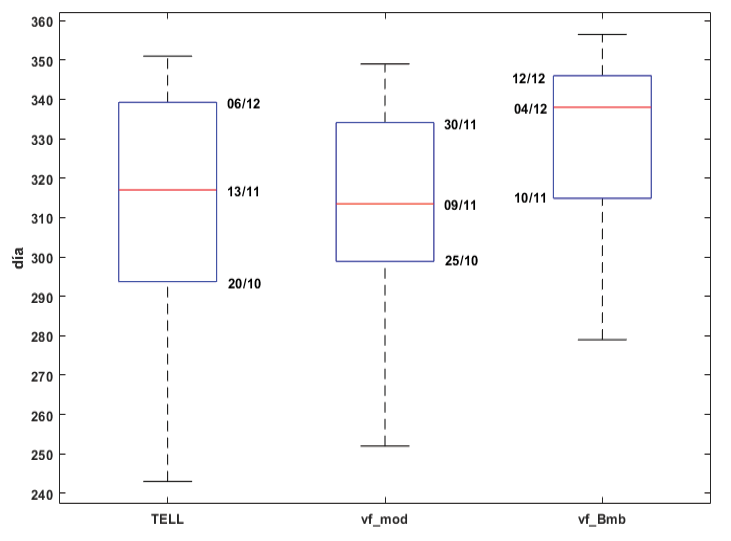
Figura 5. Diagramas de caja que del término de la estación lluviosa del promedio obtenido para todas las estaciones de la figura 1: (TELL) Resultados de la metodología de Alfaro e Hidalgo [16] (vf_mod) resultados de aplicar la metodología modificada propuesta, (vf_Bmb) resultados de aplicar la metodología propuesta por Bombardi et al. [25]. Se muestran la fecha del primer cuartil, la mediana y tercer cuartil.

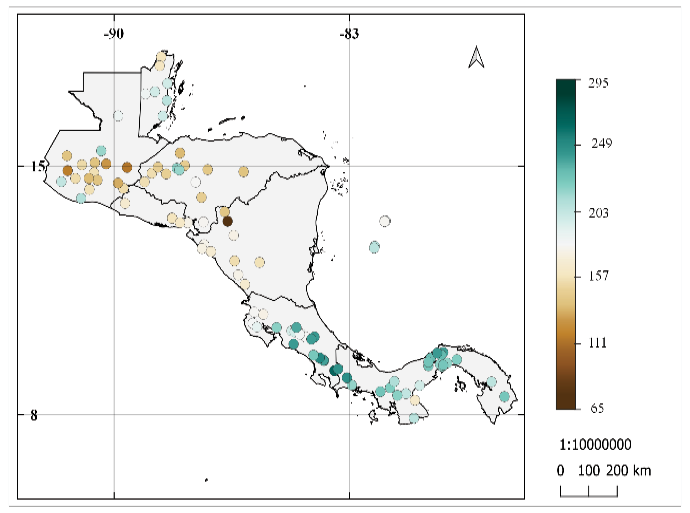
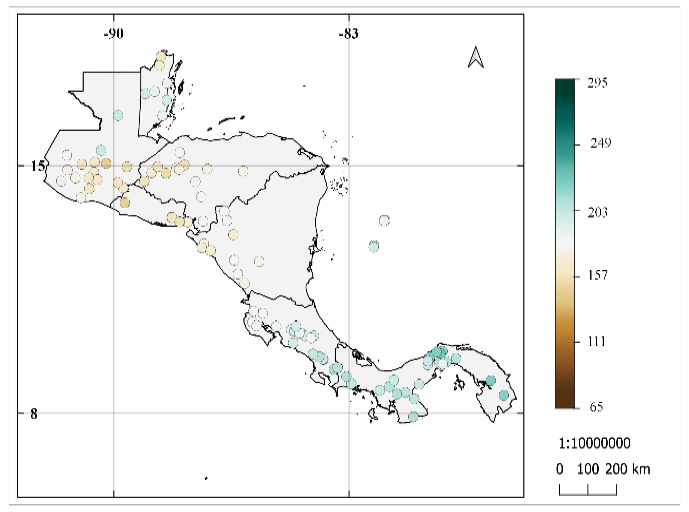
Los promedios de la duración de la época lluviosa se muestran en la figura 6, la cual está definida para cada estación como TELL − IELL + 1. Se obtuvieron resultados en su mayoría una duración prolongada de la estación lluviosa (colores más verdes) desde el centro de Costa Rica hacia el Sur y en la isla de San Andrés en las tres metodologías. Los conjuntos de datos de las diferentes metodologías muestran una duración de la estación lluviosa más reducida en promedio en estaciones en el Pacífico Norte de Costa Rica, Nicaragua, parte sur y central de Honduras, El Salvador, sur de Guatemala, y en el norte de Belice. Contrasta en la metodología utilizada por Bombardi et al. [25] estaciones en el centro y este de Belice con una duración más prolongada de la ELL. En general para estos resultados no se muestra una duración corta de la estación lluviosa (colores más cafés).

Los diagramas de caja de la figura 7 muestran que los resultados de aplicar las tres metodologías no generan valores atípicos. Para los resultados de la metodología de Alfaro e Hidalgo [16] se muestra la duración de la ELL con una mediana de 186 días, el primer cuartil de 154 días y el tercer cuartil 217 días. Para la rutina modificada propuesta la mediana es de 185 días, el primer cuartil de 169 días y el tercer cuartil de 201 días. Los resultados de la metodología de Bombardi et al. [25] muestran una mediana de 230 días, el primer cuartil de 204 días y el tercer cuartil de 250 días.

Los resultados de las 3 metodologías muestran una duración más prolongada de la época lluviosa del centro de Costa Rica hacia el sur, en estaciones en la costa este de Belice, norte de Guatemala y San Andrés. Los resultados de aplicar el criterio usado por Bombardi et al. [25] muestra en Belice una duración mayor de la época lluviosa, este método de selección del criterio pudo ser sensible a frentes fríos, provocando falsas detecciones del término o inicio de la estación lluviosa Zárate-Hernández [27]. Se muestra una zona con menor duración de la época lluviosa en Nicaragua, Honduras, El Salvador y algunas estaciones al sur de Guatemala congruente con el área del Corredor Seco Centroamericano propuesta por Quesada-Hernández et al. [28].

a)	b)
c)

Figura 6. Promedio de la duración de la época lluviosa para las 101 estaciones entre 1968 al 2012 utilizando: (a) resultados de la metodología de Alfaro e Hidalgo [16], (b) resultados de la metodología modificada propuesta, (c) resultados de la metodología utilizada por Bombardi et al. [25].

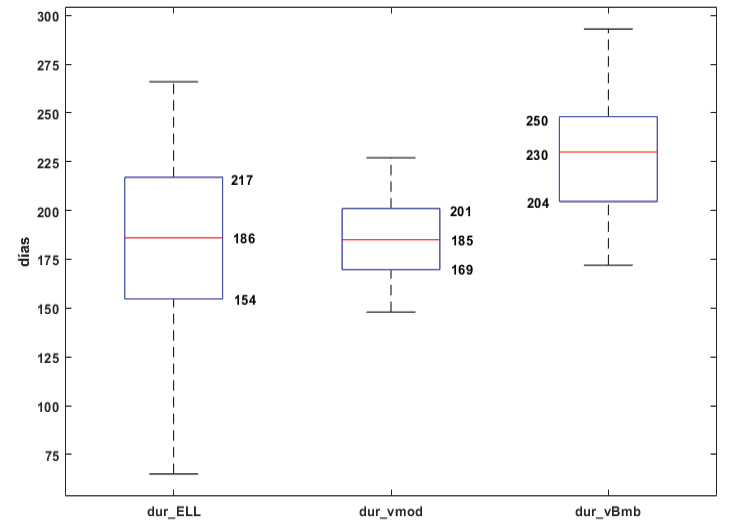
Figura 7. Diagramas de caja de la duración de la estación lluviosa del promedio obtenido para todas las estaciones de la Figura 1. (dur_ELL): resultados de la metodología de Alfaro e Hidalgo [16], (dur_vmod): metodología modificada propuesta, (vf_Bmb): metodología propuesta por Bombardi et al. [25]. Se muestran las fechas del primer cuartil, la mediana y tercer cuartil.

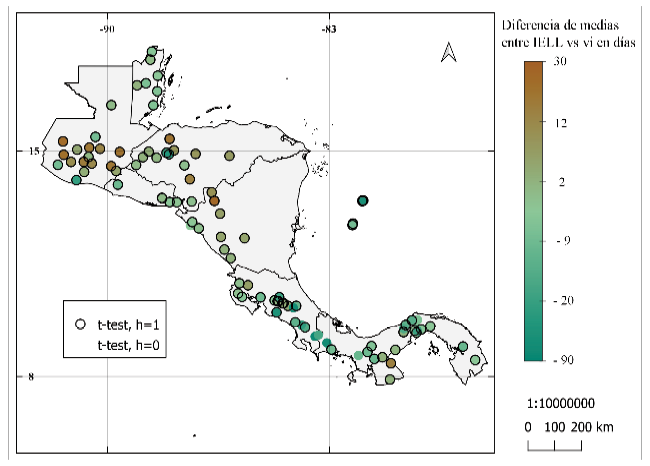
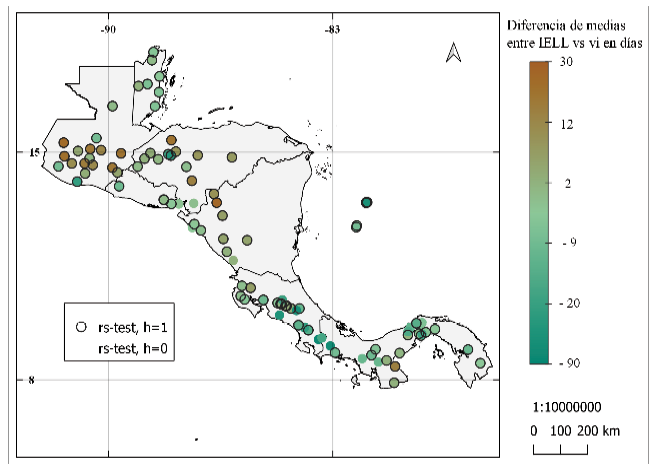
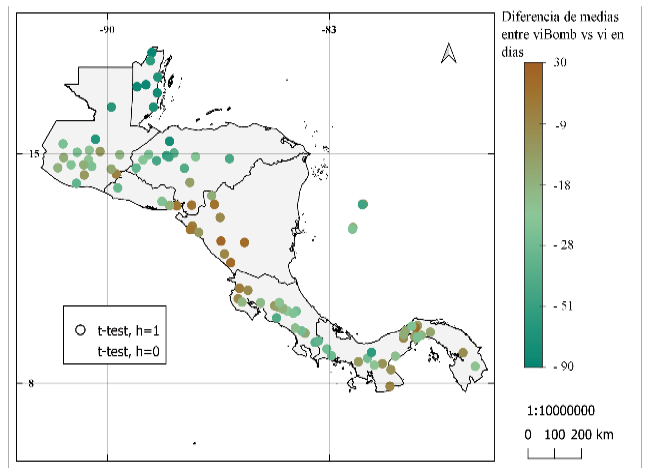
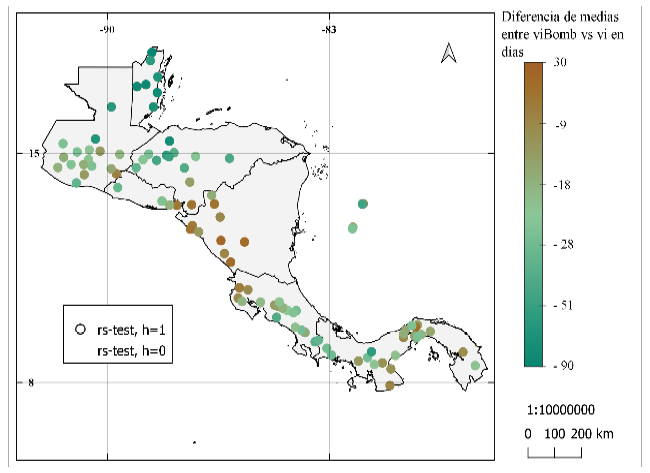
Las diferencias de medias para el IELL (figura 8) muestra diferencia hasta de 90 días para el inicio de la estación lluviosa. Entre los resultados se puede observar que la metodología modificada detecta un inicio más temprano desde Costa Rica hacia el sur, por otro lado, se observa inicios más tardíos en los resultados de Alfaro e Hidalgo [16] para estaciones en Nicaragua y alrededores. Las pruebas de diferencia de medias muestran que para la gran mayoría de las estaciones existe una diferencia significativa al 95% para la prueba t y para la prueba Wilcoxon entre los resultados de la metodología de Alfaro e Hidalgo [16] y la metodología propuesta. Ambas pruebas de diferencia de medias arrojaron resultados de series con promedio estadísticamente igual entre metodología propuesta y la utilizada por Bombardi et al. [25] (figura 8c y 8d).

a)	b)
c)	d)

Figura 8. Diferencia de los promedios del inicio de la época lluviosa entre: (a) y (b) los resultados de la metodología de Alfaro e Hidalgo [16] y la metodología propuesta (c) y (d) resultados de la metodología de Bombardi et al. [25] y resultados de la metodología propuesta. Se muestra la prueba de hipótesis de diferencia de medias: prueba t en (a) y (c), prueba de suma de rangos Wilcoxon en (b) y (d). Donde h = 0, no se puede rechazar la hipótesis nula (las series provienen de muestras con medias iguales) y h = 1, se rechaza la hipótesis nula (las series no provienen de muestras con medias iguales), ambas pruebas con nivel de significancia al 95%.

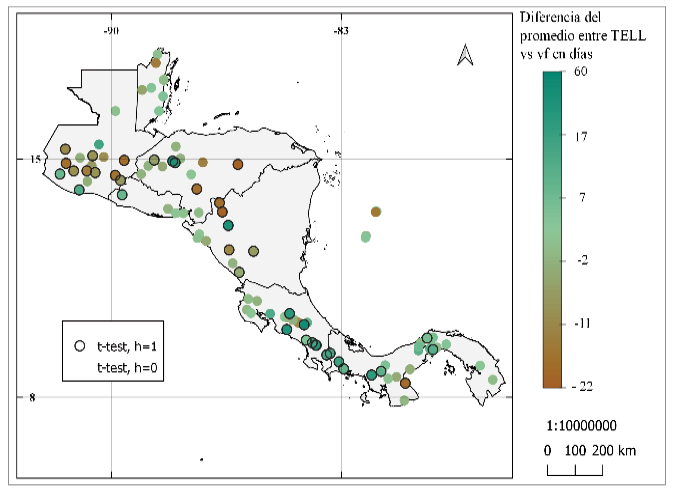
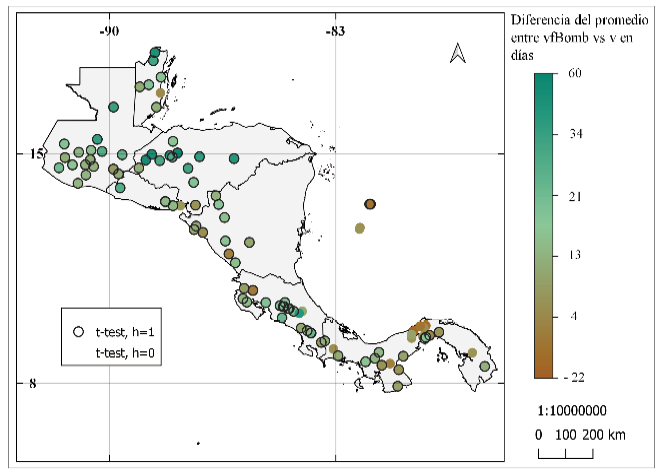
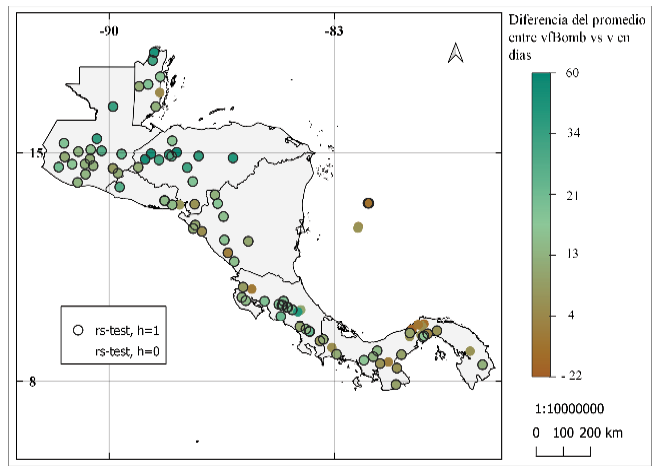
Se obtuvieron diferencias de hasta 60 días para el TELL (figura 9). Diferencias cercanas a cero se muestran entre los resultados de Alfaro e Hidalgo [16] y la metodología modificada, en Panamá, el Pacífico Norte de Costa Rica, la costa Pacífico de Nicaragua, San Andrés, Honduras y en Belice. Los resultados de la prueba t y Wilcoxon para estas series de tiempo mostraron que la mayoría de las series tienen promedios significativos diferentes.

a)	b)
c)	d)

Figura 9. Igual a la figura 8 para el término de la estación lluviosa.

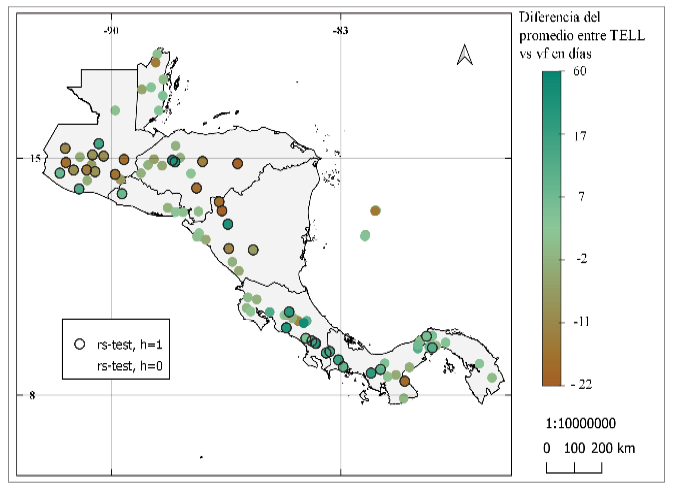
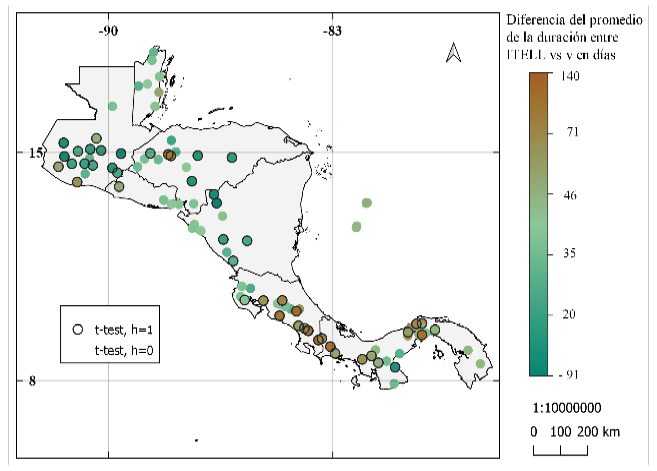
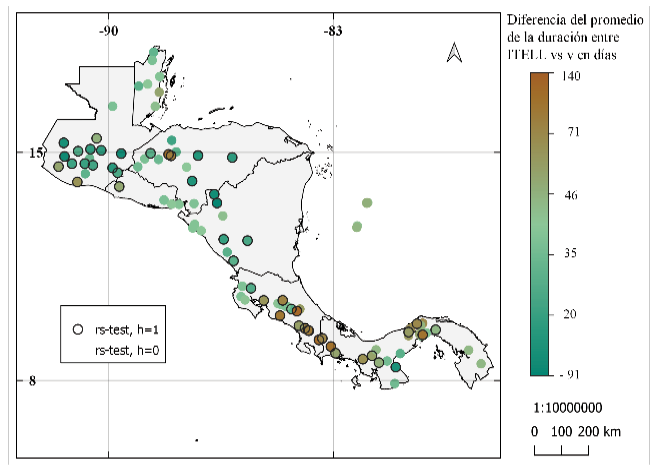
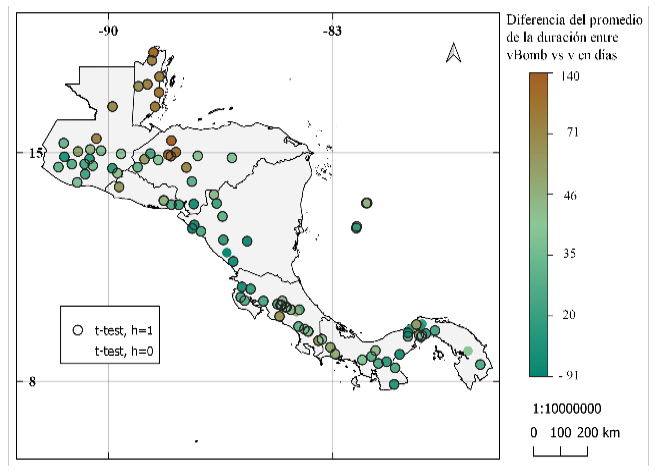
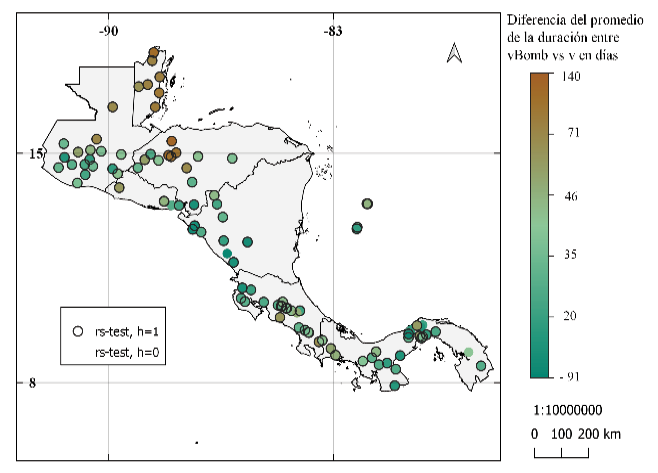
Los resultados de la diferencia de media entre las series muestran hasta 140 días entre la duración de la ELL (figura 10), los resultados entre la metodología de Alfaro e Hidalgo [16] y la metodología modificada muestran diferencias negativas al norte de América Central y diferencias más positivas desde el centro de Costa Rica hacia el sur. Entre la metodología modificada y la usada por Bombardi et al. [25] se puede notar que en Belice se tienen diferencias más positivas. Diferencias cercanas a cero se obtuvieron cerca del Canal de Panamá, Pacífico Norte de Costa Rica y Nicaragua. Para estos mapas se observa una predominancia en diferencias significativas entre los promedios de sus series.

a)	b)
c)	d)

Figura 10. Diferencia del promedio de la duración de la época lluviosa entre: (a) y (b) los resultados de la metodología de Alfaro e Hidalgo [16] y la metodología propuesta, (c) y (d) resultados de la metodología de Bombardi et al. [25] y resultados de la metodología propuesta. Se muestra la prueba de hipótesis de diferencia de medias: prueba t en (a) y (c), prueba de suma de rangos Wilcoxon en (b) y (d). Donde h = 0, no se puede rechazar la hipótesis nula (las series provienen de muestras con medias iguales) y h = 1, se rechaza la hipótesis nula (las series no provienen de muestras con medias iguales), ambas pruebas con nivel de significancia al 95%.

Conclusiones

Este estudio comparó los resultados del IELL, TELL y la duración de la ELL de tres metodologías donde se observa que para el IELL entre resultados de la metodología de Alfaro e Hidalgo [16] y la metodología propuesta una mediana muy similar, siendo los resultados de Alfaro e Hidalgo [16] más dispersos en la detección de un IELL más temprano y más tardío para el mismo conjunto de estaciones (figuras 2a, 2b y 3). La metodología de Bombardi et al. [25] detecta el IELL con una mediana casi 20 días y con inicios más tempranos que las otras dos metodologías. Esto indica que esta metodología es susceptible a frentes fríos detectando falsos inicios de la ELL (figuras. 4c y 5).

Al igual que en el IELL, los resultados para el TELL entre de la metodología de Alfaro e Hidalgo [16] y la metodología propuesta poseen una mediana muy similar, los resultados de Alfaro e Hidalgo siendo más dispersos, con TELL más tempranos (figuras 2a, 2b y 3). Los resultados de Bombardi et al. [25] arrojaron un TELL más tardío, con una mediana casi de 25 días después que las otras dos metodologías (figuras 4c y 5).

En cuanto a la duración de la ELL la mediana entre los resultados de la metodología de Alfaro e Hidalgo [16] y la metodología propuesta es casi la misma solo con un día de diferencia (186 y 185 días respectivamente), sin embargo, los resultados de Alfaro e Hidalgo [16] son mucho más dispersos que las otras metodologías (figuras 6a, 6b y 7). La metodología de Bombardi et al [25] muestra una duración de la ELL en general más larga que las otras dos metodologías, con una mediana de 230 días.

Por último, las pruebas de hipótesis realizadas muestran en su mayoría que las series del IELL, TELL entre los resultados de la metodología de Alfaro e Hidalgo [16] y la metodología propuesta son significativamente diferentes y con diferencia hasta de 90 días en algunas estaciones (figuras 8a, 8b, 9a y 9b). Los resultados de la duración de la ELL entre estas metodologías muestran diferencia de hasta 140 días en algunas estaciones. Las pruebas de hipótesis de diferencia de media entre los resultados de la metodología de Bombardi et al. [25] y la metodología propuesta son estadísticamente similares solo para el IELL (figuras 8c y 8d ).

Tomando en cuenta las figuras 2, 4 y 6, el valor de tendencia central y la dispersión de las figuras 3, 5 y 7, se determina que la metodología propuesta genera resultados estadísticamente similares en tendencia central a los determinados por Alfaro e Hidalgo [16] y con menos variabilidad. Por otro lado, la metodología aplicada por Bombardi et al. [25] detecta falsos inicios de la ELL, extienden el TELL y alarga la duración de la ELL en el sur de América Central, norte de Honduras y en Belice.

Agradecimientos

Al programa de Posgrado en Ciencias de la Atmósfera de la Universidad de Costa Rica (SP5905). La presente investigación se elaboró en el marco de varios proyectos inscritos en la Vicerrectoría de Investigación y Acción Social de la Universidad de Costa Rica: 805-C0-610 (apoyado por el Fondo de Estímulo), EC-497 (apoyado por el fondo de extensión FEES-CONARE), 805-C0-074, 808-C2-103 y 805-B9-454 (apoyado por el Fondo de Grupos).

Referencias

[1] Z. Zuo, S. Yang, Z. Z. Hu, R. Zhang, W, Wang, B. Huang, and F. Wang, “Predictable patterns and predictive skills of monsoon precipitation in Northern Hemisphere summer in NCEP CFSv2 reforecasts”, Climate dynamics, 40(11-12), 3071-3088, 2013.

[2] Saha, Suranjana and Coauthors, “The NCEP Climate Forecast System Version 2”, Journal of Climate J. Climate, 27, 2185-2208. doi: http://dx.doi.org/10.1175/JCLI-D-12-00823.1, 2014.

[3] D. B. Enfield, and E. J. Alfaro, “The dependence of Caribbean rainfall on the interaction of the tropical Atlantic and Pacific Oceans”, Journal of Climate, 12(7), 2093-2103, 1999.

[4] S. G. Díaz-Alcántara, “Inicio de las lluvias de verano en las costas del Pacífico Mesoamericano”, tesis de Licenciatura, Universidad Autónoma de México, 2019.

[5] A. Pendergrass, Angeline, and National Center for Atmospheric Research Staff (Eds). Last modified 01 Jul 2016. “The Climate Data Guide: GPCP (Daily): Global Precipitation Climatology Project.”, 2016.

[6] E. Alfaro, L. Cid, and D. Enfield, “Relaciones entre el inicio y el término de la estación lluviosa en Centroamérica y los Océanos Pacífico y Atlántico Tropical”, Investigaciones Marinas, 26, 59-69, 1998.

[7] E. Alfaro, and L. Cid, “Análisis de las anomalías en el inicio y el término de la estación lluviosa en Centroamérica y su relación con los océanos Pacífico y Atlántico Tropical”, Tópicos Meteorológicos y Oceanográficos, 6(1), 1-13, 1999.

[8] R. H. Gramzow, and W. K. Henry “The rainy pentads of Central America”, Journal of Applied Meteorology, 11, 637-642, 1972.

[9] K. M. Hernández, and W. Fernández, “Estudio de la evaporación para el cálculo del inicio y conclusión de la época seca y lluviosa en Costa Rica”, Tópicos Meteorológicos y Oceanográficos, 14, 18-26, 2015.

[10] R. G. Allen, L. S. Pereira, D. Raes, and M. Smith, “Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56”, Fao, Rome, 300(9), D05109, 1998.

[11] T. Nakaegawa, O. Arakawa, and K. Kamiguchi, “Investigation of climatological onset and withdrawal of the rainy season in Panama based on a daily gridded precipitation dataset with a high horizontal resolution”, Journal of Climate, 28(7), 2745-2763, 2015.

[12] P. F. Rivera-Ramos, W. A. Ochoa-Orozco, B. G. González-Chavajay, and M. R. Salguero-Barahona, “Inicio y término de la época lluviosa (IELL, TELL) en los estratos de la zona cañera de Guatemala”, Revista Tikalia, 37(2), 39-58, 2019.

[13] B. Liebmann, and J. Marengo, “Interannual variability of the rainy season and rainfall in the Brazilian Amazon Basin”, Journal of Climate, 14(22), 4308-4318, 2001.

[14] R. J. Bombardi, and L. M. Carvalho, “IPCC global coupled model simulations of the South America monsoon system”, Climate Dynamics, 33(7-8), 893, 2009.

[15] E. Alfaro, “Some Characteristics of the Annual Precipitation Cycle in Central America and their Relationships with its Surrounding Tropical Oceans”, Tópicos Meteorológicos y Oceanográficos, 9(2), 88-103, 2002.

[16] E. Alfaro, and H. Hidalgo, “Inicio de la temporada de lluvias en América Central (On the onset of the rainy season in Central America)”, Tópicos Meteorológicos y Oceanográficos, 20(1), 16-28, 2021.

[17] E. Alfaro, and J. Soley, “Descripción de dos métodos de rellenado de datos ausentes en series de tiempo meteorológicas”, Revista de Matemática: teoría y aplicaciones, 16(1), 60-75, 2009.

[18] P. Ureña, E. J. Alfaro, and J. Soley, “Propuestas metodológicas para el rellenado de datos ausentes en series de tiempo geofísicas. Guía Práctica de Uso. Technical Document.”, Centro de Investigaciones Geofísicas, Escuela de Física y Centro de Investigaciones en Ciencias del Mar y Limnología, Universidad de Costa Rica. Disponible en http://kerwa.ucr.ac.cr/, http://kimuk.conare.ac.cr/, 2016.

[19] E. Alfaro, “Caracterización del “veranillo” en dos cuencas de la vertiente del Pacífico de Costa Rica, América Central”, Revista de Biología Tropical, 62 (Supl. 4): 1-15, 2014.

[20] E. Alfaro, and H. Hidalgo, “Propuesta metodológica para la predicción climática estacional del veranillo en la cuenca del río Tempisque, Costa Rica, América Central”, Tópicos Meteorológicos y Oceanográficos, 16(1). 62-74, 2017.

[21] T. Maldonado, A. Rutgersson, E. Alfaro, J. Amador, and B. Claremar, “Interannual variability of the midsummer drought in Central America and the connection with sea surface temperatures”, Advances in Geosciences, 42, 35-50, 2016.

[22] E. Solano, “Análisis del comportamiento de los períodos caniculares en Costa Rica en algunas cuencas del Pacífico Norte y del Valle Central entre los años 1981 y 2010”, tesis de Licenciatura, Universidad de Costa Rica, 2015.

[23] F. J. Soley, F. J. “Suavizamiento de series cronológicas geofísicas con ruido blanco y rojo aditivo”, Revista de Geofísica, 41, 33-58, 1994.

[24] E. Alfaro, and D. Enfield, “The rainy season in Central America: An initial success in prediction”, IAI Newsletters, 20, 20-22, 1999.

[25] R. J. Bombardi, K. V. Pegion, J. L. Kinter, B. A. Cash, and J. M. Adams, “Sub-seasonal predictability of the onset and demise of the rainy season over monsoonal regions”, Frontiers in Earth Science, 5, 14, 2017.

[26] D. S. Wilks, “Statistical methods in the atmospheric sciences”, 4th. ed. Elsevier, 2019.

[27] E. Zárate-Hernández, “Climatología de masas invernales de aire frío que alcanzan Centroamérica y el Caribe y su relación con algunos índices Árticos.”, Tópicos Meteorológicos y Oceanográficos, 12(1), 35 – 55, 2013.

[28] L. E. Quesada-Hernández, O. D. Calvo-Solano, H. G. Hidalgo, P. M. Pérez-Briceño, and E. J. Alfaro, “Dynamical delimitation of the Central America Dry Corridor (CADC) using drought indices and aridity values”, Progress in Physical Geography, 43(5), 627-642. DOI:10.1177/0309133319860224. 2019.

---