Análisis cualitativo y cuantitativo de fosfatos de calcio por difracción de rayos-X mediante los métodos de Scherrer, Williamson-Hall y refinamiento de Rietveld

Qualitative and quantitative X-ray diffraction analysis of calcium phosphates by Scherrer, Williamson-Hall and Rietveld refinement methods

Alexánder Campos-Quirós1, Kenneth Paniagua-Murillo2, Gerardo Valladares-Castrillo3, Jorge M. Cubero-Sesin4, Luis Cordero-Arias5

Campos-Quirós, A; Paniagua-Murillo, K; Valladares-Castrillo, G; Cubero-Sesin, J.M; Cordero-Arias, L. Análisis cualitativo y cuantitativo de fosfatos de calcio por difracción de rayos-X mediante los métodos de Scherrer, Williamson-Hall y refinamiento de Rietveld. Tecnología en Marcha. Vol. 35, No 4. Octubre-Diciembre, 2022. Pág. 104-115.

https://doi.org/10.18845/tm.v35i4.5664

Palabras clave

Brushita; fosfato de calcio; monetita; precipitación química; método de Rietveld.

Resumen

Los fosfatos de calcio son materiales biocerámicos de gran importancia utilizados en el área de recubrimientos bioactivos para implantes metálicos. En el presente estudio, una muestra de fosfatos de calcio fue sintetizada mediante el método de precipitación química a partir de Ca(NO3)2 y (NH4)2HPO4. La técnica de difracción de rayos-X fue utilizada para realizar un análisis cualitativo y cuantitativo de las fases cristalinas presentes en el material mediante los métodos de Scherrer, Williamson-Hall y Rietveld. Se determinó que la muestra está constituida en un 75 % en masa de monetita (CaHPO4) y un 25 % en masa de brushita (CaHPO4.H2O), con tamaños promedio de cristalito en el orden submicrométrico. El análisis mediante microscopia electrónica de barrido muestra que las partículas se encuentran altamente aglomeradas, con un tamaño promedio de 2,8 ± 1 µm y morfología variada. El análisis elemental por espectroscopia de energía dispersiva de rayos-X reveló una relación molar calcio/fósforo (Ca/P) promedio de 0,95, lo cual concuerda con las fases cristalinas de monetita y brushita. Por último, la presencia de ambas fases se debe principalmente a los bajos niveles de pH durante la reacción y al secado de la muestra posterior al proceso de síntesis.

Keywords

Brushite; calcium phosphate; monetite; chemical precipitation; Rietveld method.

Abstract

Calcium phosphates are important bioceramic materials used for bioactive coatings for metal implants. In the present study, calcium phosphate powders were synthesized by chemical precipitation method using Ca(NO3)2 and (NH4)2HPO4. X-ray diffraction technique was used to perform a qualitative and quantitative analysis of the crystalline phases present in the material using Scherrer, Williamson-Hall, and Rietveld methods. The sample is constituted by 75 weight % of monetite (CaHPO4) and 25 weight % of brushite (CaHPO4.H2O), with an average crystallite size within the submicrometer order. Scanning electron microscopy shows agglomerated particles, with an average size of 2,8 ± 1 µm and different morphologies. Elemental analysis by energy-dispersive X-ray spectroscopy revealed an average calcium/phosphorus (Ca/P) molar ratio of 0.95, which is consistent with monetite and brushite phases. Finally, the presence of both phases is mainly attributed to the low pH during the reaction and the drying process after the synthesis.

Introducción

Los fosfatos de calcio son compuestos de gran interés debido a sus aplicaciones biomédicas. Estos materiales biocerámicos están presentes en huesos, dientes y tendones dando dureza, estabilidad y funcionalidad a dichos tejidos [1]. Algunos de ellos son ampliamente utilizados como recubrimiento para implantes óseos debido a su similitud con el hueso, biocompatibilidad y osteoconductividad [2]. Los enlaces químicos entre el hueso y estos recubrimientos permiten que los implantes metálicos de materiales como acero inoxidable y aleaciones de titanio adquieran una superficie bioactiva y se disminuya el riego de rechazo del implante por parte del cuerpo [3, 4].

Debido a su potencial en diversas aplicaciones biomédicas se ha desarrollado diversos estudios acerca de distintos métodos de síntesis. Uno de los más utilizados para la producción de muestras en forma de polvo es el método de precipitación química, debido a que el equipo requerido es sencillo, es de bajo costo y se puede obtener un material de alta pureza. [5-7]. Durante este proceso existen una serie de factores que definen el tipo de fosfato de calcio que se puede obtener, así como sus propiedades finales. Algunos de estos factores son la estequiometría, el pH, el orden y la velocidad en que se añaden los reactantes, la temperatura de la reacción y los tratamientos térmicos posteriores como secado, calcinado y sinterizado [8-10].

Debido al gran número de variables involucradas en la reacción, el método de precipitación química presenta como principal desventaja la dificultad de controlar los productos finales obtenidos, ya que se pueden formar distintas fases intermedias durante la reacción en distintas proporciones [6]. Debido a que las propiedades del material se encuentran estrechamente relacionadas con el tipo de fase cristalina, es de suma importancia realizar una caracterización cristalográfica, así como morfológica y estequiométrica de los compuestos formados.

Por esta razón, la utilización de métodos cualitativos y cuantitativos basados en difracción de rayos-X es crucial una vez finalizado el proceso de síntesis. Una herramienta muy útil en el campo de la cristalografía es el método de Scherrer, el cual se basa en cuantificar el ensanchamiento de los picos, el cual toma como referencia el ancho de los picos a media altura (FWHM) para determinar el tamaño de cristalito. Este ensanchamiento consta de dos componentes: una debido a la muestra en estudio y otra atribuida al instrumento o difractómetro utilizado [12]. Por esta razón es importante aislar la componente debido a la muestra utilizando la siguiente ecuación [16]:

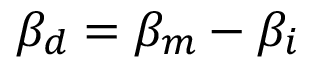(1)

Donde 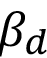es el ensanchamiento debido a la muestra, 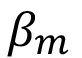es el ensanchamiento total medido directamente del difractograma y 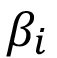es el ensanchamiento debido al instrumento. Para calcular 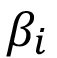se utiliza el valor de FWHM obtenido del difractograma de una muestra estándar. Además, la ecuación (1) toma en cuenta que la forma del pico se puede modelar utilizando una función Lorentziana [16].

Una vez calculado 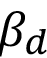se puede utilizar la ecuación de Scherrer para calcular el tamaño de cristalito para cada pico de difracción atribuido a los planos (hkl) de la siguiente forma [1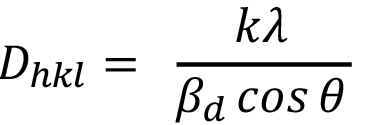2]:

(2)

Donde 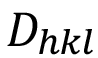es el tamaño de cristalito en nanómetros, k es una constante cuyo valor es 0.94, l es la longitud de onda de la radiación de rayos-X utilizada y q es la mitad del ángulo de Bragg (2q). Es importante aclarar que 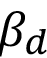y q deben estar en radianes para realizar este cálculo.

Otro método cuantitativo ampliamente utilizado es el de Williamson-Hall [17]. Este método considera que el ensanchamiento del pico debido a la muestra (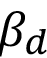) se divide en dos componentes. Una de estas componentes describe una función Lorentziana y es atribuida al tamaño de cristalito. La otra, se modela mediante una función Gaussiana y corresponde a la contribución de las microdeformaciones presentes en el material. Para separar ambas componentes puede utilizarse la siguiente ecuación:

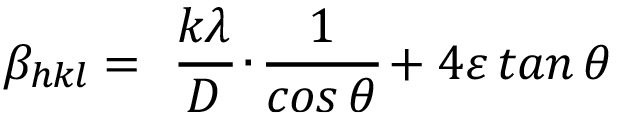(3)

Donde 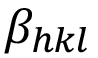es el ancho de pico a medio altura atribuido a la muestra, D es el valor promedio de tamaño de cristalito y e es el valor de microdeformaciones. La ecuación (3) puede reescribirse con el fin de realizar un ajuste lineal de los datos de la siguiente forma:

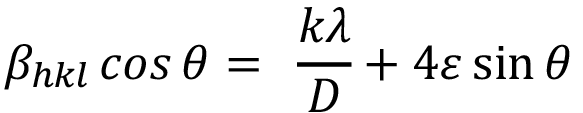(4)

La ecuación (4) es también conocida como modelo de deformación uniforme, debido a que asume un comportamiento isotrópico de los cristales [18]. Del ajuste lineal de los datos se extrae el valor de microformaciones a partir del valor de la pendiente y el valor de tamaño de cristalito a partir del valor del intercepto con el eje y.

Los métodos de Scherrer y Williamson-Hall constituyen un primer acercamiento a los valores de tamaño de cristalito y microdeformaciones. Sin embargo, al analizar únicamente algunos picos de difracción la información que brindan es limitada. El método de Rietveld, por otra parte, es capaz de analizar todo el patrón de difracción y obtener un análisis cuantitativo más detallado. Esta técnica tiene por objetivo ajustar un modelo estructural de una o varias fases cristalinas con el difractograma obtenido experimentalmente en un proceso iterativo por medio de mínimos cuadrados [12,13]. Esto quiere decir que parámetros como la fracción de cada fase presente, parámetros de red, tamaño de cristalito y microdeformaciones pueden ser refinados en reiteradas ocasiones hasta un difractograma calculado similar al obtenido experimentalmente.

El presente estudio aborda el desarrollo de un análisis cualitativo y cuantitativo de una muestra de fosfatos de calcio sintetizada mediante el método de precipitación química a partir de Ca(NO3)2 y (NH4)2HPO4. Para esto se utiliza la técnica de microscopía electrónica de barrido para analizar la morfología y el tamaño de partícula. Además, se realizó un análisis elemental mediante espectroscopía de energía dispersiva de rayos-X. Por último, se emplearon diversos métodos cuantitativos basados en difracción de rayos-X como lo son Scherrer, Williamson-Hall y Rietveld. Se identificaron las fases presentes y se prestó especial atención a la fracción de cada fase en el material, así como sus respectivos valores de tamaño promedio de cristalito, microdeformación y parámetros de red.

Materiales y métodos

Síntesis por precipitación química

La muestra de fosfatos de calcio fue sintetizada mediante el método de precipitación química utilizando una disolución de Ca(NO3)2 (Sigma Aldrich, ACS grado reactivo). La reacción fue llevada a cabo a una temperatura de 25°C y el pH fue controlado utilizando NH4OH (Sigma Aldrich, ACS grado reactivo), siendo 3,95 y 4,99 los valores iniciales y finales respectivamente. La proporción de (NH4)2HPO4 (Sigma Aldrich, ACS grado reactivo) fue controlada para obtener una proporción molar calcio-fósforo (Ca/P) inicial de 1,67. Seguidamente, el precipitado obtenido fue reposado a 25°C con un posterior secado a 60°C. Por último, la muestra en forma de polvo obtenida no fue sometida a ningún tipo de calcinado ni sinterizado posterior a su síntesis.

Difracción de rayos-X (XRD)

La técnica de difracción de rayos-X fue utilizada con el fin de identificar las fases cristalinas presentes en la muestra fosfatos de calcio. Para dicho fin se utilizó un difractómetro de polvos PANalytical Empyrean con una geometría Bragg-Brentano, radiación Cu-Ka, un tamaño de paso de 0,007° y una velocidad de análisis de 0,3 °/min. La identificación de las fases presentes, así como la obtención de la información cristalográfica correspondiente fue realizada consultando la base de datos PDF-4. Además, se obtuvo un patrón de difracción de una muestra estándar de LaB6 bajo las mismas condiciones de ensayo utilizadas para la muestra de fosfatos de calcio.

Método de Scherrer

El método de Scherrer fue utilizando para calcular el tamaño de cristalito a partir del difractograma experimental utilizando la ecuación (2). El valor de ensanchamiento de los picos 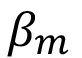fue medido a partir del difractograma de la muestra de fosfatos de calcio, mientras el valor de 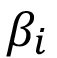fue medido a partir del difractograma de la muestra estándar de LaB6. Ambas mediciones se realizaron utilizando el software Match! 3. Se utilizaron 4 picos de difracción con valores de 2q entre 30° y 55° para obtener el valor de tamaño de cristalito en cada fase. Además, no se utilizaron picos en ángulos menores a 30° para evitar el efecto de la asimetría presente en ángulos bajos.

Método de Williamson-Hall

El método de Williamson-Hall fue utilizado para la determinación del tamaño promedio de cristalito, así como el valor de microdeformaciones mediante el ajuste lineal de la ecuación (4). En este caso se utilizaron los mismos 4 picos de difracción utilizados para el análisis por el método de Scherrer.

Método de Rietveld

Para el refinamiento de Rietveld fue utilizado el software GSAS-II [19]. Los parámetros instrumentales fueron calculados a partir del refinamiento del patrón de difracción de la muestra estándar de LaB6. El difractograma de la muestra de fosfatos de calcio fue analizado sin realizar sustracción de la radiación CuKa2 ni la radiación de fondo. El fondo fue modelado mediante una función polinomial Chebyschev de orden seis y se definieron los límites de refinamiento de 2q = 10° – 55°. Se fijó el valor de factor de escala del histograma en 1 y se permitió la variación de la fracción de cada fase presente, del desplazamiento de la muestra, de los parámetros de red, del tamaño de cristalito y de las microdeformaciones de ambas fases. El ajuste de la intensidad de los picos fue realizado utilizando una extracción de LeBail.

Microscopia electrónica de barrido y espectroscopía de energía dispersiva de rayos-X (SEM-EDS)

La técnica de microscopía electrónica de barrido (SEM) acoplada con espectroscopía de energía dispersiva de rayos-X (EDS) fue utilizada para el estudio de la morfología de las partículas de fosfatos de calcio, así como su análisis elemental, esto bajo una tensión de aceleración de 15 kV.

Resultados

SEM-EDS

La figura 1 muestra las micrografías obtenidas mediante la técnica de SEM de la muestra de fosfatos de calcio en forma de polvo. En la figura 1(a) se evidencia que las partículas se encuentran altamente aglomeradas. En la figura 1(b) se observan algunas partículas a mayor detalle, las cuales presentan una morfología variada tipo piramidal y acicular con algunas formas tipo hojuelas. Las partículas presentan una distribución homogénea de tamaño en el área analizada, con un tamaño promedio de 2,8 ± 1 µm, obtenido a partir de la medición de más de 50 partículas en la figura 1(b). Además, los resultados del análisis elemental EDS revelaron una relación molar Ca/P promedio de 0,95.

Figura 1. Micrografías SEM de una muestra de fosfatos de calcio sintetizada por precipitación química tomadas a una magnificación de (a) x300 y (b) x1500 aumentos.

XRD

Identificación de fases

La figura 2 muestra el difractograma obtenido a partir de la muestra en forma de polvo de fosfatos de calcio. Se logran apreciar picos bien definidos y con poco ensanchamiento, lo que podría indicar pocos defectos cristalinos en el material. Las fases identificadas corresponden a monetita, CaHPO4 (98-000-2745) y brushita, CaHPO4.H2O (98-010-9193). Cabe destacar que no fueron identificados picos que pudieran estar relacionados con contaminantes ni fases secundarias en menor proporción.

Figura 2. Difractograma de rayos-X de una muestra de fosfatos de calcio sintetizada por precipitación química.

Método de Scherrer

En el cuadro 1 se muestran los valores de posición y ensanchamiento de los picos de cada fase utilizados para el cálculo del tamaño de cristalito mediante la ecuación (2). El valor de 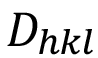hace referencia a la longitud promedio de las zonas en el material que presentan difracción coherente, tomando en cuenta las condiciones de análisis utilizadas [20]. No debe confundirse con el tamaño de grano o de partícula, los cuales pueden no coincidir con el valor de 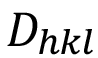. En este caso el valor promedio de tamaño de cristalito de las fases monetita y brushita fue de 360 nm y 555 nm respectivamente.

Cuadro 1. Tamaño de cristalito obtenido por el método de Scherrer de una muestra de fosfatos de calcio sintetizada mediante precipitación química

Fase	(hkl)	2q(°)	bm(°)	bi(°)	bd(°)	Dhkl (nm)
Monetita	(211)	30,408	0,0963	0,0797	0,0166	518
	(202)	35,989	0,0997	0,0775	0,0223	391
	(2)	40,035	0,1038	0,0763	0,0275	321
	(114)	52,979	0,1202	0,0761	0,0441	210
Brushita	(220)	34,119	0,0883	0,0781	0,0101	859
	(24)	36,864	0,0912	0,0772	0,014	625
	(221)	45,213	0,0987	0,0758	0,0229	392
	(260)	48,442	0,1029	0,0762	0,0266	342

Método de Williamson-Hall

La figura 3 muestra los resultados obtenidos del ajuste lineal para el cálculo del tamaño promedio de cristalito y el valor de microdeformaciones presentes en la muestra. Se obtuvieron valores altos de coeficiente de correlación R2 cercanos a 1 en ambos casos, lo cual indica un buen ajuste de los datos. El valor de microdeformación puede ser extraído directamente de la pendiente de la curva siendo 0,0005622 para la fase de monetita y 0,0005339 para la brushita. Por otra parte, la intercepción con el eje y permite calcular el tamaño promedio de cristalito D el cual es 457 nm para monetita y 321 nm para la brushita.

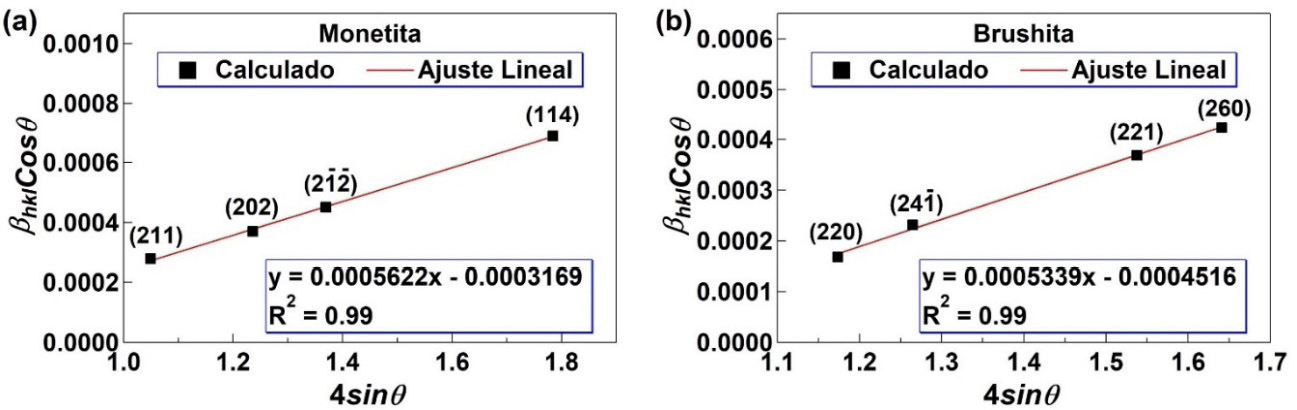
Figura 3. Análisis cuantitativo por el método de Williamson-Hall de una muestra de fosfatos de calcio sintetizada por precipitación química.

Método de Rietveld

En la figura 4 se muestra el difractograma experimental y el calculado mediante el método de Rietveld para la muestra de fosfatos de calcio. Se obtuvo un valor de wR = 6,232, lo cual indica un buen ajuste del patrón calculado con respecto al experimental. Se observa como el pico más intenso a 2q = 11,65°, correspondiente a los planos (020) de la brushita, presenta la mayor diferencia entre el difractograma experimental y el calculado, lo cual se evidencia por su alto valor de error. Además, se indican la posición de los picos de difracción utilizados para los análisis mediante los métodos de Scherrer y Williamson-Hall.

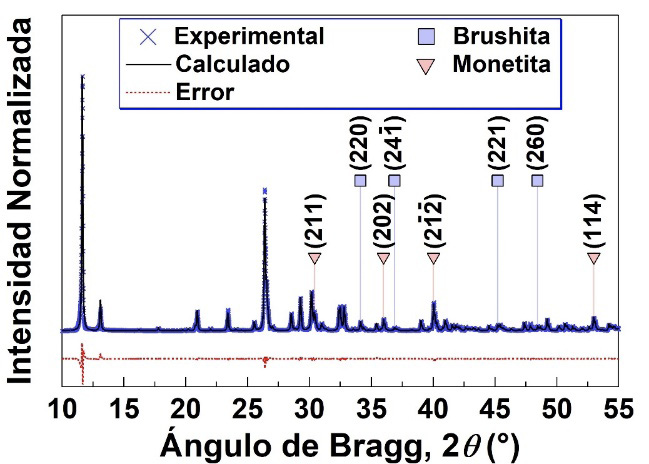
Figura 4. Difractograma experimental y calculado por el método de Rietveld para una muestra de fosfatos de calcio sintetizada por precipitación química. Se indica la posición de los picos de difracción de la monetita y la brushita utilizados para el análisis por el método de Scherrer y el método de Williamson-Hall.

Los resultados mediante el análisis por el método de Rietveld revelaron que la brushita presenta un tamaño promedio de cristalito D = 615 nm y un valor de microdeformación e = 0,002882. Por otra parte, la monetita presenta un tamaño promedio de cristalito D = 290 nm con un valor de microdeformación e = 0,002092. Debido a que los parámetros instrumentales U, V, W, X y Y no fueron variados, el ensanchamiento de los picos se debe al efecto de parámetros microestructurales y por ende los valores de D y e se atribuyen al efecto de la muestra [21]. Además, el análisis cuantitativo reveló que la muestra de fosfatos de calcio está constituida por 75 % y 25 % en masa de monetita y brushita respectivamente.

En el cuadro 2 se muestran los parámetros de red de ambas fases obtenidos luego del refinamiento por el método de Rietveld. Según las fichas cristalográficas, la monetita presenta una estructura cristalina triclínica con un grupo espacial P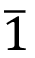 mientras la brushita es monoclínica con un grupo espacial es C1c1. Como se puede observar en el cuadro 2, hay una tendencia general a presentar parámetros de red ligeramente mayores a los reportados en las fichas cristalográficas. Esto concuerda con los resultados obtenidos por el método de Williamson-Hall en donde los valores de microdeformaciones presentan valores positivos para ambas fases, indicando una expansión de la red cristalina. Por otra parte, existe una baja diferencia entre los parámetros cristalográficos teóricos y los calculados mediante el método de Rietveld, lo que indica que la posición de los picos de dichas fases concuerda bien con la posición de los picos obtenidos en el difractograma experimental. Esto evidencia una correcta identificación de las fases presentes en el material.

Cuadro 2. Parámetros de red teóricos y calculados por el método de Rietveld de las fases de brushita y monetita sintetizadas por precipitación química.

	Teórico		Rietveld
Parámetro	Monetita	Brushita	Monetita	Brushita
a (Å)	6,627	6,358	6,634	6,361
b (Å)	6,910	15,180	6,913	15,190
c (Å)	6,998	5,812	6,993	5,821
α (°)	76,180	90,000	76,051	90,000
β (°)	83,660	118,512	83,777	118,527
γ (°)	88,330	90,000	88,391	90,000

Discusión

Relación molar Ca/P y pH de la reacción

La relación molar Ca/P establecida por la estequiometria de la reacción durante la síntesis fue de 1,67. Sin embargo, el análisis elemental EDS reveló una relación molar promedio de 0,95. Mondal et al. reportan que una proporción molar Ca/P de 1 corresponde a fosfatos de calcio como la brushita y la monetita, lo cual concuerda con la identificación de fases mediante la técnica de difracción de rayos-X [22]. Además, reportes previos indican que a medida que la reacción se lleva a cabo en un medio ácido existe una tendencia a la disminución en el valor de la relación molar Ca/P de los productos de la reacción [1,23].

Esto indicaría que la disminución en la proporción molar Ca/P de 1,67 a 0,95 se debe principalmente al efecto del pH final de la reacción, el cual fue de 4,99.

Con respecto a la formación de las fases presentes en el material, la precipitación de brushita se ve favorecida a niveles de pH entre 4 y 6 por lo que la presencia de esta fase se podría explicar debido al valor de pH final de la reacción [24]. Por otra parte, la monetita puede ser obtenida mediante la eliminación de moléculas de agua de la estructura de la brushita, por lo que el proceso de secado de los polvos, llevado a cabo luego de la síntesis, podría ser el principal responsable de la formación de esta fase [25]. Estudios previos han demostrado que ambas fases permiten la proliferación de osteoblastos en su superficie y son biocompatibles, lo que favorece su uso en recubrimiento de implantes ortopédicos [26]. Adicionalmente, se ha reportado que el uso de recubrimientos de brushita y monetita sobre implantes metálicos de Mg confiere una buena resistencia a la corrosión en comparación al implante sin recubrimiento [27]. Los recubrimientos biomédicos a partir de brushita y la monetita presentan una gran versatilidad debido a las diferentes propiedades mecánicas, intercambio de iones Ca2+ y PO43-, solubilidad, crecimiento celular, entre otras, que pueden ser obtenidas al utilizar ambas fases [26, 28]. Estas propiedades pueden ser controladas variando la proporción en masa de cada fase en el material, por lo que el análisis cuantitativo por difracción de rayos-X se vuelve una herramienta crucial en la determinación de la relación composición-propiedades.

SEM

La gran aglomeración de las partículas observadas mediante SEM puede ser explicado debido al proceso de maduración de Ostwald, el cual suele producir la aglomeración en polvos sintetizados por precipitación [29]. Este mecanismo se basa en que las partículas grandes crecen a expensas de las más pequeñas. Esto se debe a la mayor solubilidad que presentan las partículas de menor tamaño, lo que hace posible su difusión hacia las partículas de mayor tamaño. Este mecanismo de crecimiento de partículas tiene como objetivo disminuir el área superficial de las partículas dispersas y puede estar acompañado de otros procesos como la coagulación/coalescencia, que también favorecen la aglomeración de las partículas [30].

Estudios previos acerca de la distribución del tamaño de partícula indican que esta puede variar entre 0.6 µm y 30 µm en el caso de fosfatos de calcio sintetizados mediante precipitación química sin aplicar ningún tratamiento térmico [31]. Estos valores concuerdan con el tamaño de partícula obtenido mediante SEM de 2,8 ± 1 µm, el cual se encuentra cercano al valor promedio reportado por Marchi et al. Cabe resaltar que, el valor de tamaño de partícula no es comparable al tamaño de cristalito obtenido mediante los métodos de Scherrer, Williamson-Hall y Rietveld debido a que cada partícula puede contener uno o varios cristalitos. Sin embargo, el tamaño de partícula es un parámetro importante que puede afectar las propiedades mecánicas, la reactividad con el medio, temperatura de sinterizado entre otros [31].

Comparación entre los métodos de Scherrer, Williamson-Hall y Rietveld

Como se puede observar en el cuadro 3, los tres métodos muestran un tamaño de cristalito que se mantiene en el orden submicrométrico. Además, coinciden en que el valor de microdeformaciones es muy similar entre ambas fases. De estos valores se puede inferir que ambas fases presentan una baja deformación microestructural lo cual indica que existen pocas imperfecciones cristalinas tales como dislocaciones. Como las partículas se obtuvieron por precipitación química, no han sido sometidas a esfuerzos mecánicos ni tratamientos térmicos a altas temperaturas. Por esta razón es de esperar que sus esfuerzos internos y microdeformaciones sean bajos [32].

Por último, las variaciones obtenidas en los valores de tamaño de cristalito y microdeformaciones se deben principalmente a que los métodos de Scherrer y Williamson-Hall utilizan únicamente algunos picos de difracción para el análisis, mientras el método de Rietveld considera todo el patrón de difracción. Esto le permite al método de Rietveld tomar en cuenta un mayor número de picos distribuidos en un amplio rango de posiciones 2q brindando mayor información acerca de la muestra como parámetros de red y fracción de fases. Sin embargo, los métodos de Scherrer y Williamson-Hall pueden ser utilizados como un paso previo para corroborar los resultados obtenidos mediante el refinamiento por el método de Rietveld.

Cuadro 3. Comparación entre los parámetros cristalagáficos obtenidos mediante los métodos de Scherrer, Williamson-Hall y Rietveld para las fases de monetita y brushita.

	Scherrer	Williamson-Hall		Rietveld
Fase	D (nm)	D (nm)		D (nm)
Monetita	360	457	0,0005622	290	0,002092
Brushita	555	321	0,0005339	615	0,002882

Conclusiones

El análisis cualitativo y cuantitativo mediante las técnicas de XRD y SEM-EDS fue llevado a cabo exitosamente para una muestra de fosfatos de calcio sintetizada por el método de precipitación química. A continuación, se detallan los principales hallazgos obtenidos:

•Las micrografías SEM revelaron que las partículas se encuentran aglomeradas, con una morfología variada y un tamaño promedio de 2,8 ± 1 µm. Por otra parte, el análisis elemental mediante EDS permitió determinar que la relación molar Ca/P para la muestra en polvo de fosfatos de calcio concuerda con los valores reportados para las fases de monetita y brushita, las cuales fueron identificadas mediante la técnica de XRD.

•La formación de brushita se atribuye principalmente al valor bajo de pH de la reacción, el cual favorece la precipitación de esta fase. Además, el proceso de secado permitió la eliminación de moléculas de agua en la brushita, dando lugar a la formación de monetita.

•Los métodos de Scherrer, Williamson-Hall y Rietveld permitieron calcular los valores promedio de tamaño de cristalito los cuales se encuentran en el orden submicrométrico. Además, los métodos de Williamson-Hall y Rietveld revelan valores bajos de microdeformaciones, lo cual coincide con lo esperado para muestra sintetizadas mediante precipitación química, las cuales presentan pocas imperfecciones cristalinas.

•Se demostró que el análisis cuantitativo por medio del método de Rietveld es una herramienta crucial en la caracterización de fosfatos de calcio donde diferentes parámetros durante la síntesis y posterior procesamiento de la muestra pueden afectar la formación de distintas fases cristalinas, así como las proporciones de cada fase presentes en el material.

Agradecimientos

Agradecemos a Esteban Rodríguez Hernández de la Escuela de Ciencia e Ingeniería de Materiales por facilitar los ensayos experimentales de difracción de rayos-X y a Luis Alvarado Marchena del Laboratorio Institucional de Microscopía por facilitar la ejecución del análisis de microscopia electrónica de barrido y espectroscopía de energía dispersiva de rayos-X.

Referencias

[1] S. V. Dorozhkin, and M. Epple, “Biological and medical significance of calcium phosphates,” Angew. Chem Int. Ed., vol. 41, no. 17, pp. 3130–3146, 2002, doi: 10.1002/1521-3773(20020902)41:17<3130::AID-ANIE3130>3.0.CO;2-1

[2] M. L. dos Santos, C. dos Santos Riccardi, E. de Almeida Filho, and A. C. Guastaldi, “Calcium phosphates of biological importance based coatings deposited on Ti-15Mo alloy modified by laser beam irradiation for dental and orthopedic applications,” Ceram. Int., vol. 44, no. 18, pp. 22432–22438, 2018, doi: 10.1016/j.ceramint.2018.09.010.

[3] D. Navarro da Rocha et al., “Bioactivity of strontium-monetite coatings for biomedical applications,” Ceram. Int., vol. 45, no. 6, pp. 7568–7579, 2019, doi: 10.1016/j.ceramint.2019.01.051.

[4] F. Pishbin, L. Cordero-Arias, S. Cabanas-Polo, and A. R. Boccaccini, Bioactive polymer-calcium phosphate composite coatings by electrophoretic deposition. Elsevier Ltd, 2015.

[5] T. T. T. Pham et al., “Impact of physical and chemical parameters on the hydroxyapatite nanopowder synthesized by chemical precipitation method,” Adv. Nat. Sci. Nanosci. Nanotechnol., vol. 4, no. 3, 2013, doi: 10.1088/2043-6262/4/3/035014.

[6] S. Koutsopoulos, “Synthesis and characterization of hydroxyapatite crystals: A review study on the analytical methods,” J. Biomed. Mater. Res., vol. 62, no. 4, pp. 600–612, 2002, doi: 10.1002/jbm.10280.

[7] B. Ben-Nissan, “Biomimetics and bioceramics,” in Learning from nature how to design new implantable biomaterials: from biomineralization fundamentals to biomimetic materials and processing routes., R. L. Reis and S. Weiner, Eds. Netherlands: Klumer Academic Publishers, 2004, pp. 89–103.

[8] L. Montastruc, C. Azzaro-Pantel, B. Biscans, M. Cabassud, and S. Domenech, “A thermochemical approach for calcium phosphate precipitation modeling in a pellet reactor,” Chem. Eng. J., vol. 94, no. 1, pp. 41–50, 2003, doi: 10.1016/S1385-8947(03)00044-5.M.

[9] R. Kumar, K. H. Prakash, P. Cheang, and K. A. Khor, “Temperature driven morphological changes of chemically precipitated hydroxyapatite nanoparticles,” Langmuir, vol. 20, no. 13, pp. 5196–5200, 2004, doi: 10.1021/la049304f.

[10] P. Ferraz, F. J. Monteiro, and C. M. Manuel, “Hydroxyapatite nanoparticles: A review of preparation methodologies,” J. Appl. Biomater. Funct. Mater. vol. 2, no. 2, pp. 74–80, 2004, doi: 1722-6899/074-07$15.00/0.

[11] H. M. Rietveld, “An Algol program for the refinement of nuclear and magnetic structures by the profile method.,” Netherlands, 1969.

[12] G. Will, “The Rietveld method,” in Powder diffraction: the Rietveld method and the two-stage methof, Germany: Springer, 2006, pp. 41–72.

[13] G. S. Girolami, “Powder X-ray diffraction,” in X-ray crystallography, USA: University Science Books, 2016, pp. 439–450.

[14] P. Scherrer, “Bestimmung der Größe und der inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen,” Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Math. Klasse, vol. 1918, pp. 98–100, 1918.

[15] Match! - Phase Identification from Powder Diffraction, Crystal Impact - Dr. H. Putz & Dr. K. Brandenburg GbR, Kreuzherrenstr. 102, 53227 Bonn, Germany, https://www.crystalimpact.de/match

[16] A. Monshi, M. R. Foroughi, and M. R. Monshi, “Modified Scherrer Equation to Estimate More Accurately Nano-Crystallite Size Using XRD,” World J. Nano Sci. Eng., vol. 02, no. 03, pp. 154–160, 2012, doi: 10.4236/wjnse.2012.23020.S.

[17] G. K. Williamson and W. H. Hall, “X-ray line broadening from filed aluminium and wolfram,” Acta Metall., vol. 1, no. 1, pp. 22–31, 1953, doi: 10.1016/0001-6160(53)90006-6.

[18] D. Nath, F. Singh, and R. Das, “X-ray diffraction analysis by Williamson-Hall, Halder-Wagner and size-strain plot methods of CdSe nanoparticles- a comparative study,” Mater. Chem. Phys., vol. 239, no. August 2019, p. 122021, 2020, doi: 10.1016/j.matchemphys.2019.122021.

[19] B. H. Toby and R. B. Von Dreele, “GSAS-II: The genesis of a modern open-source all purpose crystallography software package,” J. Appl. Crystallogr., vol. 46, no. 2, pp. 544–549, 2013, doi: 10.1107/S0021889813003531.

[20] S. A. Kube et al., “Combinatorial study of thermal stability in ternary nanocrystalline alloys,” Acta Mater., vol. 188, pp. 40–48, 2020, doi: 10.1016/j.actamat.2020.01.059.

[21] B. D. Cullity and S. R. Stock, Elements of X-ray diffraction, Thrid edit. USA: Pearson Education Limited, 2014.

[22] S. Mondal, A. Dey, and U. Pal, “Low temperature wet-chemical synthesis of spherical hydroxyapatite nanoparticles and their in situ cytotoxicity study,” Adv. nano Res., vol. 4, no. 4, pp. 295–307, 2016, doi: 10.12989/anr.2016.4.4.295.

[23] Raynaud, E. Champion, D. Bernache-Assollant, and P. Thomas, “Calcium phosphate apatites with variable Ca/P atomic ratio I. Synthesis, characterisation and thermal stability of powders,” Biomaterials, vol. 23, no. 4, pp. 1065–1072, 2002, doi: 10.1016/S0142-9612(01)00218-6.

[24] O. Mekmene, S. Quillard, T. Rouillon, J. M. Bouler, M. Piot, and F. Gaucheron, “Effects of pH and Ca/P molar ratio on the quantity and crystalline structure of calcium phosphates obtained from aqueous solutions,” Dairy Sci. Technol., vol. 89, no. 3–4, pp. 301–316, 2009, doi: 10.1051/dst/2009019.

[25] F. Tamimi, Z. Sheikh, and J. Barralet, “Dicalcium phosphate cements: Brushite and monetite,” Acta Biomater., vol. 8, no. 2, pp. 474–487, 2012, doi: 10.1016/j.actbio.2011.08.005.

[26] U. Klammert, T. Reuther, C. Jahn, B. Kraski, A.C. Kübler, U. Gbureck, Cytocompatibility of brushite and monetite cell culture scaffolds made by three-dimensional powder printing, Acta Biomater. 5 (2009) 727–734. doi:10.1016/j.actbio.2008.08.019.

[27] S. Shadanbaz, J. Walker, T.B.F. Woodfield, M.P. Staiger, G.J. Dias, Monetite and brushite coated magnesium: In vivo and in vitro models for degradation analysis, J. Mater. Sci. Mater. Med. 25 (2014) 173–183. doi:10.1007/s10856-013-5059-2.

[28] H. Zhou, L. Yang, U. Gbureck, S.B. Bhaduri, P. Sikder, Monetite, an important calcium phosphate compound–Its synthesis, properties and applications in orthopedics, Acta Biomater. 127 (2021) 41–55. doi:10.1016/j.actbio.2021.03.050.

[29] A. Chandrasekar, S. Sagadevan, and A. Dakshnamoorthy, “Synthesis and characterization of nano-hydroxyapatite (n-HAP) using the wet chemical technique,” Int. J. Phys. Sci., vol. 8, no. 32, pp. 1639–1645, 2013, doi: 10.5897/IJPS2013.3990.

[30] T. K. N. Hoang, L. Deriemaeker, B. Van La, and R. Finsy, “Monitoring the simultaneous ostwald ripening and solubilization of emulsions,” Langmuir, vol. 20, no. 21, pp. 8966–8969, 2004, doi: 10.1021/la049184b.

[31] J. Marchi, P. Greil, J. C. Bressiani, A. Bressiani, and F. Müller, “Influence of synthesis conditions on the characteristics of biphasic calcium phosphate powders,” Int. J. Appl. Ceram. Technol., vol. 6, no. 1, pp. 60–71, 2009, doi: 10.1111/j.1744-7402.2008.02254.x.

[32] A. Khorsand Zak, W. H. Abd. Majid, M. E. Abrishami, and R. Yousefi, “X-ray analysis of ZnO nanoparticles by Williamson-Hall and size-strain plot methods,” Solid State Sci., vol. 13, no. 1, pp. 251–256, 2011, doi: 10.1016/j.solidstatesciences.2010.11.024.

---