Optimización del punto de operación de un impulsor axial sin eje central en flujo sanguíneo
Optimization of the operating point of an axial impeller without central shaft in blood flow
Johanna Muñoz-Pérez1
Fecha de recepción: 17 de julio de 2021
Fecha de aprobación: 29 de octubre de 2021
Muñoz-Pérez, J. Optimización del punto de operación de un impulsor axial sin eje central en flujo sanguíneo. Tecnología en Marcha. Vol. 35-3. Julio-Setiembre 2022. Pág. 48-59. https://doi.org/10.18845/tm.v35i3.5625
https://doi.org/10.18845/tm.v35i3.5625
Palabras clave
Diseño de experimentos; gráfica superpuesta de contorno; gráfica de interacción; impulsor axial; optimización de respuesta.
Resumen
Este artículo abarca la obtención de los modelos matemáticos para las respuestas de deformación volumétrica, diferencia de presión y caudal de un impulsor axial diseñado para un dispositivo de asistencia ventricular. Dicho impulsor posee una geometría novedosa que requiere la validación de su comportamiento a nivel estructural y de dinámica de fluidos. Basándose en las especificaciones requeridas para la aplicación se obtiene el punto de operación óptimo del impulsor en cuanto a su velocidad de rotación, material y velocidad de salida del flujo sanguíneo. Asimismo, se obtiene el rango de valores de los factores que cumplen con las especificaciones. Dentro de los materiales incluidos se tiene el Platino y el polímero biocompatible Peek. El análisis se realiza por medio de un diseño de experimentos factorial completo, con resultados obtenidos previamente utilizando herramientas de simulación. La obtención de los modelos matemáticos se realiza por medio de la depuración de los factores de entrada y sus interacciones.
Keywords
Design of experiments; superimposed contour plot; interaction plot; axial impeller; response optimization.
Abstract
This article covers the obtention of the mathematical models for the volumetric strain, pressure difference, and flow responses of an axial impeller designed for a ventricular assist device. This impeller has a novel geometry that requires the validation of its behavior at the structural and fluid dynamics level. Based on the specifications required for the application, the optimal operating point of the impeller is obtained in terms of its rotational velocity, material, and blood flow output velocity. Likewise, the range of values of the factors that meet the specifications is obtained. Among the materials included are Platinum and the biocompatible polymer Peek. The analysis is carried out by means of a full factorial design of experiments, with results previously obtained using simulation tools. Obtaining the mathematical models is carried out by debugging the input factors and their interactions.
Introducción
En Costa Rica, el 29% de las enfermedades mortales están relacionadas con padecimientos cardiacos [1]. Los dispositivos de asistencia ventricular se utilizan usualmente como un tratamiento temporal de uno de dichos padecimientos: la insuficiencia cardiaca [2, 3]. En esta condición, el corazón pierde su capacidad para funcionar como una bomba de sangre y proveer el gasto cardiaco requerido, es decir, la cantidad de sangre que demanda el cuerpo por minuto [4, 5].
Dentro del Área Académica de Ingeniería Mecatrónica del Instituto Tecnológico de Costa Rica se realiza el diseño de un dispositivo de asistencia ventricular con una nueva geometría en su impulsor y material de fabricación. Dicha modificación plantea la utilización de un impulsor sin eje central con el objetivo de estudiar su comportamiento frente al modelo comercial de impulsor con eje central. Además, se pretende utilizar un polímero biocompatible para fabricar el conjunto, lo que facilitaría la producción y abarataría los costos del producto.
En este desarrollo es requerido establecer si el nuevo diseño de impulsor logra cumplir con los requerimientos de funcionamiento a nivel de fluidos, supliendo un caudal de sangre de al menos 4 L/min y una diferencia de presión entre la entrada y salida del impulsor de al menos 40 mmHg [6]. De igual forma, la utilización de un nuevo material requiere comprobar que se mantiene su integridad estructural al someterse a las presiones que ejerce el fluido sobre las paredes del impulsor, así como a la presión característica del ciclo cardiaco [7, 8].
Actualmente, la utilización de herramientas computacionales para el estudio de fenómenos físicos permite un primer abordaje a las inquietudes planteadas. Estos paquetes de software discretizan la estructura por estudiar y resuelven las ecuaciones apropiadas según la física de estudio [9]. Los resultados de este artículo se obtienen utilizando el software COMSOL® para los parámetros de respuesta: deformación volumétrica, diferencia de presión y caudal del impulsor axial sin eje central para los materiales de Platino y el polímero biocompatible Teca Peek [10, 11].
Por medio de un diseño de experimentos factorial utilizando la herramienta Minitab® se determinan los factores y las interacciones entre los mismos que establecen cada parámetro de respuesta, para de esta forma obtener las ecuaciones de regresión correspondientes. Finalmente, se optimizan las respuestas para cumplir con los criterios de funcionamiento del impulsor axial sin eje central y analizar su factibilidad de uso en un dispositivo de asistencia ventricular [12, 13].
Metodología
La investigación desarrollada se clasifica como cuantitativa, con alcance exploratorio, de diseño no experimental y de tipo transversal [14]. El planteamiento del diseño de experimentos inicia por la descripción de las variables involucradas. Al requerir obtener las salidas de deformación volumétrica, diferencia de presión y caudal se desprende que las entradas corresponden a la velocidad de rotación del impulsor, la velocidad de salida del flujo sanguíneo y el tipo de material. En los cuadros 1 y 2 se detalla la definición de las entradas y salidas del diseño de experimentos, basado en el desarrollo en [6].
Cuadro 1. Descripción de los parámetros de salida del diseño de experimentos.
|
Respuesta |
Símbolo |
Especificación |
|
Deformación volumétrica (% o adimensional) |
εv |
0.6 % o inferior |
|
Diferencia de presión (mmHg) |
ΔP |
40 – 60 |
|
Caudal (L/min) |
Q |
4 - 5,5 |
Cuadro 2. Descripción de los parámetros de entrada del diseño de experimentos.
|
Nombre |
Factor |
Nivel bajo |
Nivel medio |
Nivel alto |
Efecto esperado |
|
Velocidad de rotación del impulsor (rpm) |
A |
7 500 |
9 000 |
10 500 |
A mayor velocidad de rotación aumenta la deformación volumétrica y la diferencia de presión |
|
Velocidad de salida del flujo sanguíneo (m/s) |
B |
0,25 |
0,625 |
1,00 |
A mayor velocidad de salida aumenta la deformación volumétrica y el caudal, pero disminuye la diferencia de presión |
|
Material |
C |
Peek |
No aplica |
Platino |
La deformación volumétrica del Platino debe ser menor a la del Peek |
Una vez establecidas las variables se describe el proceso para su obtención. En esta etapa de la investigación se aprovechan las ventajas de la simulación mediante el método de elementos finitos. Si bien es cierto que los modelos computacionales se asemejan, pero no son iguales a los modelos físicos, es precisamente esta característica la que permite obtener información reduciendo los tiempos de cómputo. Dentro del software COMSOL® se trabaja con las físicas de mecánica estructural y mecánica de fluidos realizando su integración como se muestra en la figura 1 [15, 16].
Básicamente, se inicia con una simulación de mecánica de fluidos en donde aún no se ha definido un material para la estructura, debido a que el resultado deseado corresponde a perfiles de velocidad, vorticidad entre otros y al campo de presiones que ejerce el fluido sobre la estructura. Este campo de presiones se utiliza como condición de frontera en una simulación de mecánica estructural donde se contempla el material del conjunto de impulsión. De esta forma, el resultado de la simulación corresponde a la geometría deformada por las presiones ejercidas sobre la estructura. La geometría deformada se importa a una nueva simulación de mecánica de fluidos para estudiar el efecto a nivel del comportamiento del fluido que causó la deformación.
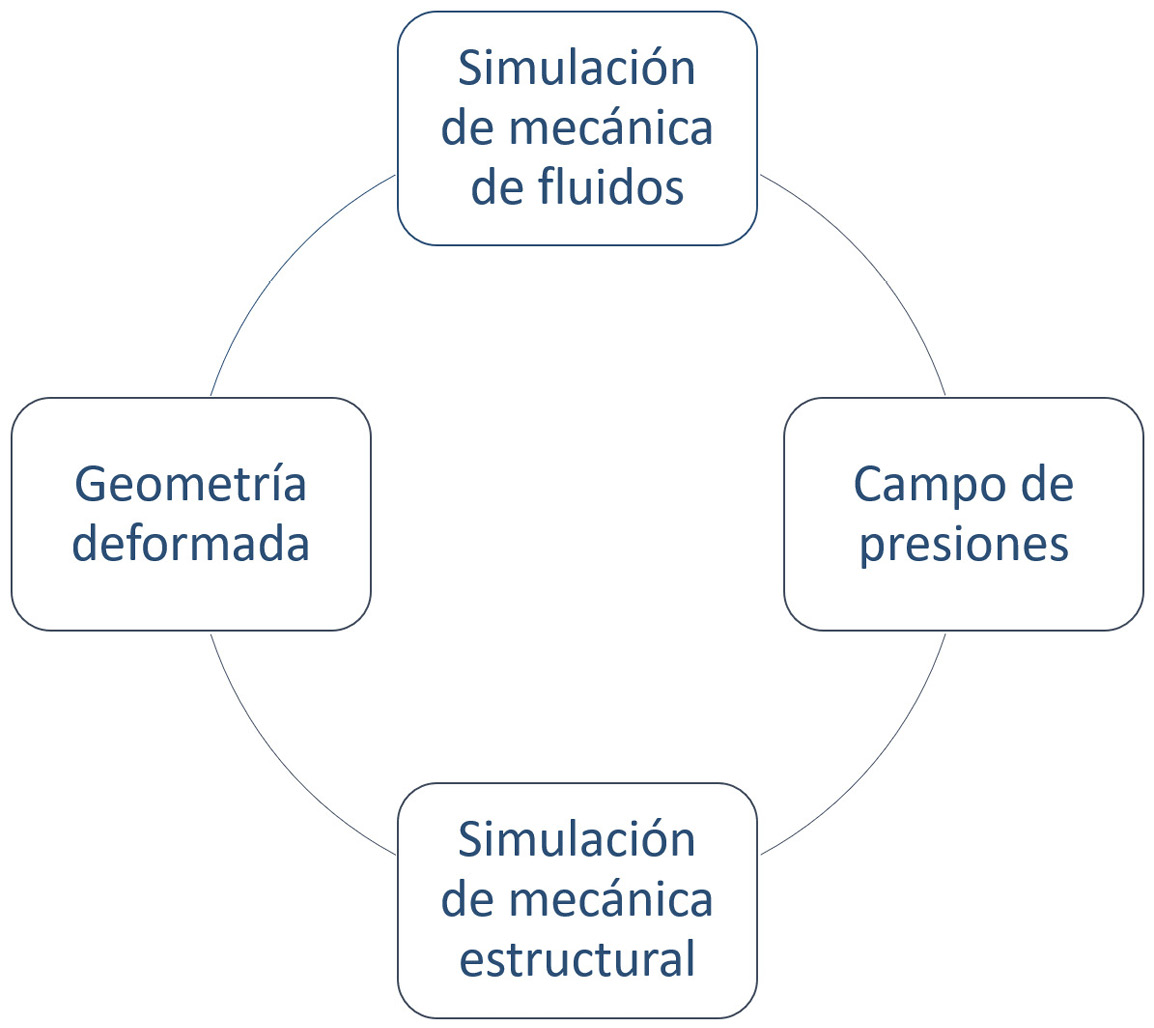
Figura 1. Integración de la mecánica estructural y la mecánica de fluidos.
Por último, se realiza la descripción del diseño de experimentos. Debido a que se cuenta con tres factores y dos niveles por cada factor se plantea un diseño de experimentos factorial completo 23 lo que equivale a ocho experimentos para una repetición completa de las combinaciones de los factores. Sin embargo, con el fin de aumentar los grados de libertad requeridos para calcular el cuadrado medio del error se añaden dos puntos centrales, uno por cada nivel del factor categórico del material. De esta forma se realizan un total de 10 experimentos [17].
Análisis de resultados
En la creación del diseño factorial completo 23 se define un bloque, una repetición y dos puntos centrales para obtener la matriz del experimento del cuadro 3 que se presenta según el orden estándar de las corridas. Seguidamente, se realiza un primer análisis de las respuestas utilizando un nivel de significancia α = 0,05 para identificar los factores e interacciones de factores que definen cada respuesta.
Cuadro 3. Matriz del diseño de experimentos.
|
Factores |
Respuestas |
||||
|
Material |
Vsal (m/s) |
Vrot (rpm) |
εv (x10-6) |
ΔP (mmHg) |
Q (L/min) |
|
Peek |
0,25 |
7 500 |
89,407 |
30,310 |
2,0142 |
|
Peek |
0,25 |
10 500 |
145,99 |
67,288 |
2,0142 |
|
Peek |
1,00 |
7 500 |
101,43 |
0,953 |
8,0568 |
|
Peek |
1,00 |
10 500 |
208,33 |
15,723 |
8,0568 |
|
Pt |
0,25 |
7 500 |
2,5525 |
30,014 |
2,0142 |
|
Pt |
0,25 |
10 500 |
4,2946 |
67,719 |
2,0142 |
|
Pt |
1,00 |
7 500 |
2,8966 |
0,984 |
8,0568 |
|
Pt |
1,00 |
10 500 |
5,9384 |
16,117 |
8,0568 |
|
Peek |
0,625 |
9 000 |
136,35 |
37,000 |
5,0355 |
|
Pt |
0,625 |
9 000 |
3,8807 |
36,921 |
5,0355 |
Este primer análisis de varianza arroja que para la deformación volumétrica la interacción triple es la menos significativa, mientras que para la diferencia de presión la interacción triple no es significativa. Además, para el caudal la respuesta depende solamente del factor de velocidad de salida. En el caso de la curvatura, se obtiene que la deformación volumétrica y el caudal poseen un comportamiento lineal, mientras que para la diferencia de presión se rechaza la hipótesis nula de linealidad.
Un segundo análisis de varianza se realiza sin considerar la interacción triple (ABC) y los puntos centrales dentro del modelo. Esta decisión se toma debido a que se desea realizar una optimización en una respuesta continua al final del análisis. Si se mantienen los puntos centrales se discretiza la respuesta y se dificulta la optimización. En este segundo análisis se observa que para las respuestas es posible excluir la interacción doble entre la velocidad de salida y el material (BC).
Posteriormente, se realiza un tercer análisis de varianza sin considerar la interacción triple (ABC), los puntos centrales y la interacción doble entre la velocidad de salida y el material (BC), dando como resultado cuatro grados de libertad para el término de error. Los diagramas de Pareto de efectos estandarizados de las figuras 2 y 3 corresponden a las respuestas de deformación volumétrica y diferencia de presión. En estos diagramas se observa que los factores A, B, C, AB y AC son los más significativos.
Debe recordarse que, al depurar tres respuestas con el fin de realizar una optimización final, se agregan o eliminan interacciones entre factores simultáneamente en las tres respuestas. Por esta razón, la interacción doble BC se excluye gracias a que no es significativa en ninguna de las respuestas, condición que no se cumple con el resto de las interacciones dobles. En las figuras 2 y 3 se observa que las interacciones dobles AC y AB son significativas en las respuestas, por lo cual los gráficos de efectos principales son secundarios y la prioridad de interpretación se tiene en los gráficos de interacción entre factores.

Figura 2. Diagrama de Pareto de efectos estandarizados para la deformación volumétrica.

Figura 3. Diagrama de Pareto de efectos estandarizados para la diferencia de presión.
En las figuras 4 y 5 se observan la gráfica de efectos principales y la gráfica de interacciones dobles para la deformación volumétrica. La figura 4 muestra que la deformación volumétrica aumenta con el aumento de la velocidad de rotación y la velocidad de salida, siendo más notorio el cambio en el caso de la velocidad de rotación. Sin embargo, el material es el factor más influyente en la respuesta, para el caso del Peek se obtienen los mayores valores de deformación volumétrica.
La interacción BC se incluye dentro de la figura 5, pero no dentro del modelo final, por lo tanto, se representa con un fondo gris. Se observa que en la interacción AB el valor de la deformación volumétrica aumenta al aumentar la velocidad de rotación, pero el incremento tiende a ser más pronunciado para la mayor velocidad de salida. Para el caso de la interacción AC, el aumento de la velocidad de rotación causa un incremento en la deformación volumétrica en el material Peek, mientras que para el Platino no se observa la interacción entre ambos factores.
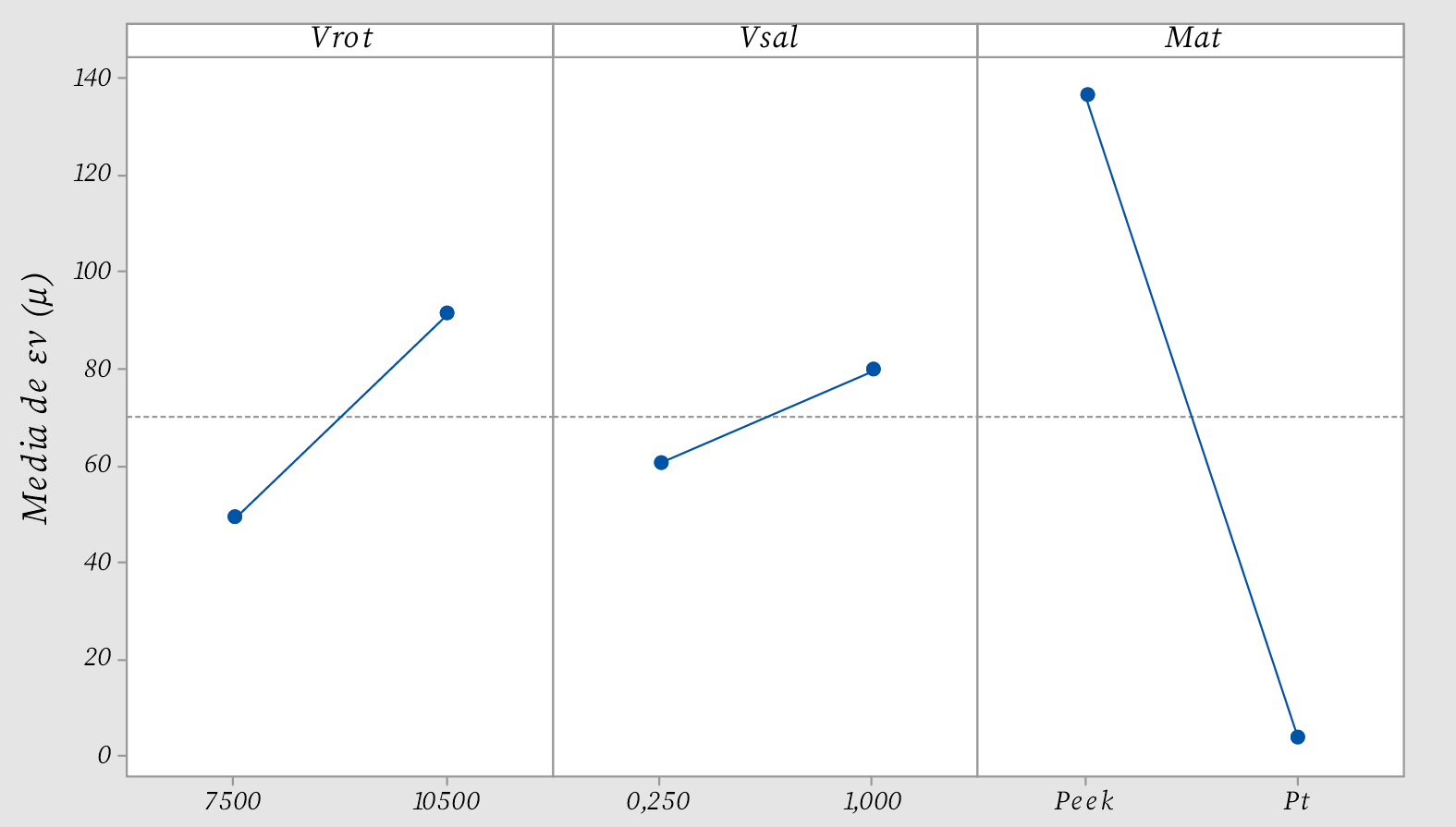
Figura 4. Gráfica de efectos principales para la deformación volumétrica.
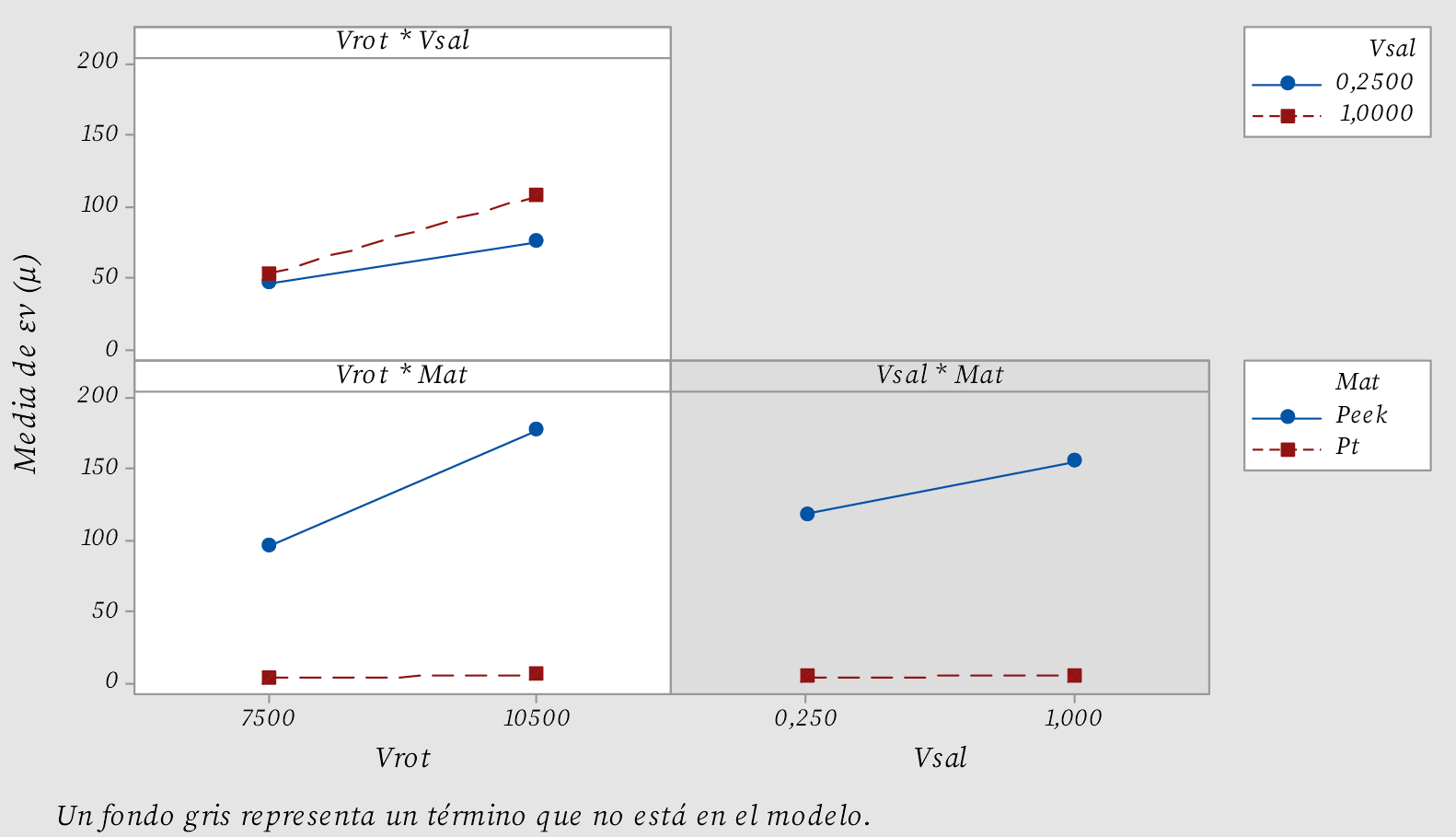
Figura 5. Gráfica de interacciones dobles para la deformación volumétrica.
En la figura 6 se presenta la gráfica de efectos principales para la diferencia de presión. El factor de la velocidad de rotación es directamente proporcional a la diferencia de presión, mientras que para la velocidad de salida la relación es inversamente proporcional. El factor del material muestra un efecto con una pendiente cercana a cero, por lo tanto, el material no influye en la respuesta de la diferencia de presión. En la gráfica de interacciones dobles de la figura 7, se obtiene que el valor máximo de A y mínimo de B provocan el valor máximo de la diferencia de presión, además de que la interacción AC no es significativa.
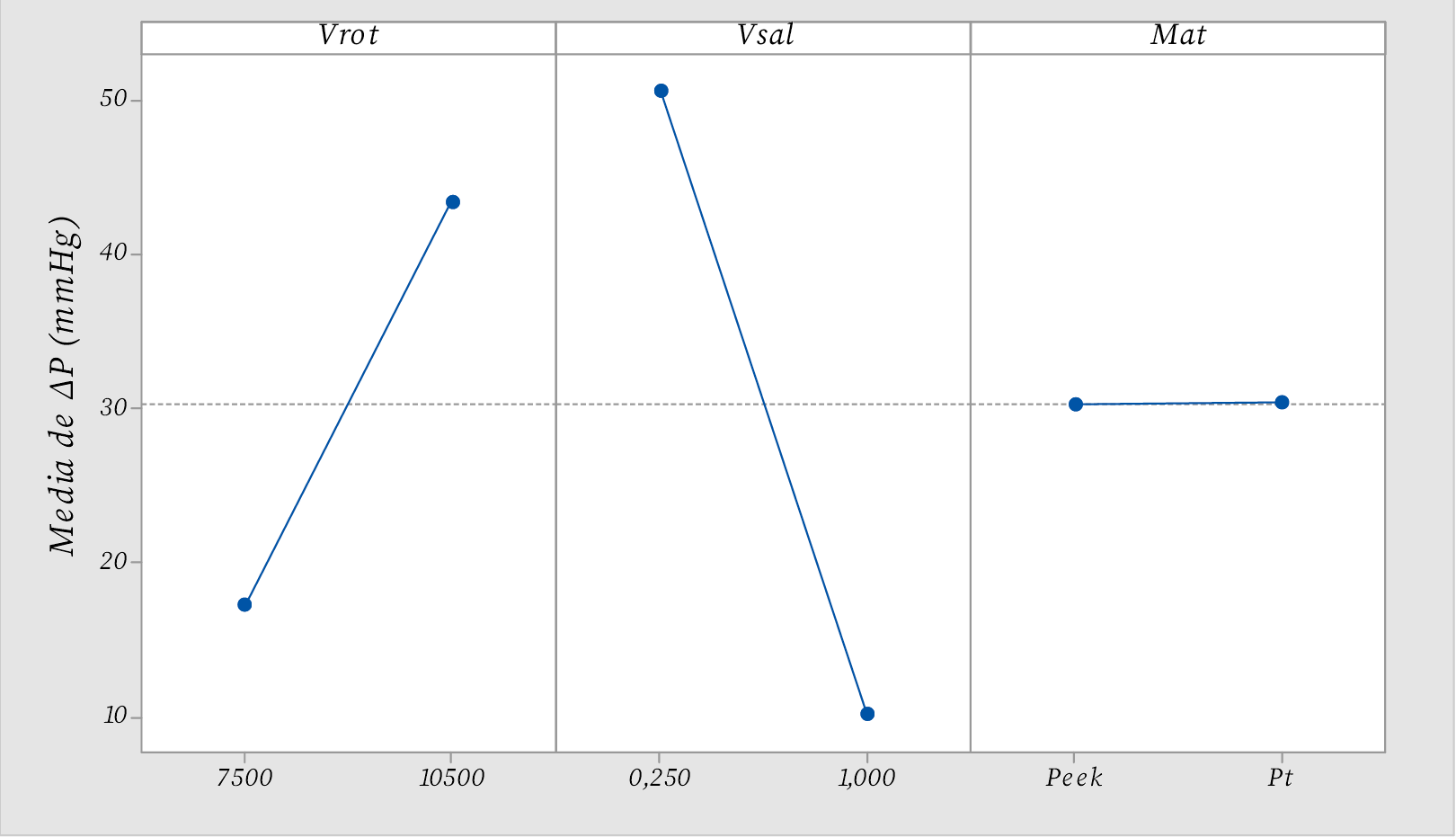
Figura 6. Gráfica de efectos principales para la diferencia de presión.
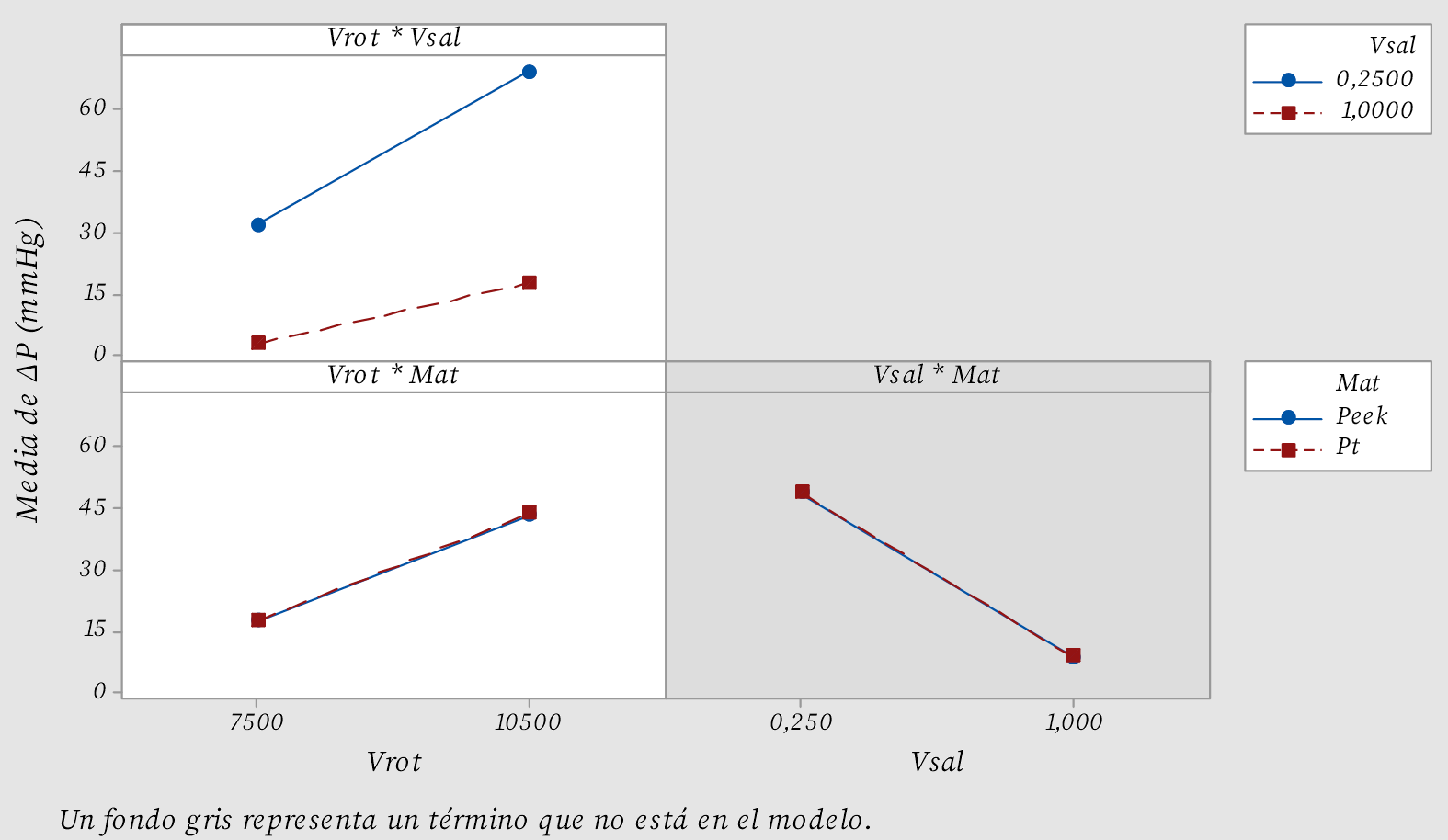
Figura 7. Gráfica de interacciones dobles para la diferencia de presión.
Para el caso de las ecuaciones de regresión, el coeficiente de determinación ajustado posee un valor de 95,91% para el modelo de εv, un valor de 95,00% para el modelo de ΔP y un valor de 100,00 % para el modelo de Q. Estos valores son superiores al 70% recomendado en la literatura [9]. Las ecuaciones de regresión 1, 2 y 3 correspondientes a cada respuesta se presentan a continuación:
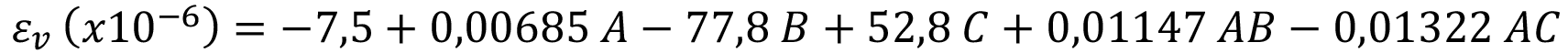 (1)
(1)
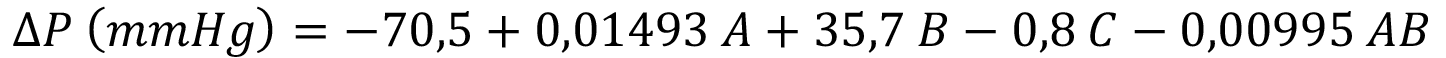 (2)
(2)
 (3)
(3)
Una vez obtenidos los modelos matemáticos se procede a la optimización de las respuestas según las especificaciones de la aplicación. Primeramente, se genera la gráfica superpuesta de contornos para las respuestas de caudal y diferencia de presión, la deformación volumétrica no se selecciona debido a que su valor se mantiene por debajo de 0.6 % en todos los casos. Además, el factor del material no tiene efecto en la diferencia de presión o el caudal, por lo que la gráfica es igual para el Platino o el Peek.
En la figura 8 se observa la gráfica superpuesta de contornos para el Peek tomando como límites del caudal un valor mínimo de 4 L/min y un valor máximo de 5,5 L/min, en el caso de la diferencia de presión el valor mínimo se establece en 40 mmHg y el valor máximo en 60 mmHg. La figura 8 permite observar que dichas especificaciones se cumplen únicamente para velocidades de rotación superiores a 9 273 rpm y velocidades de salida entre 0,4962 m/s y 0,6763 m/s.
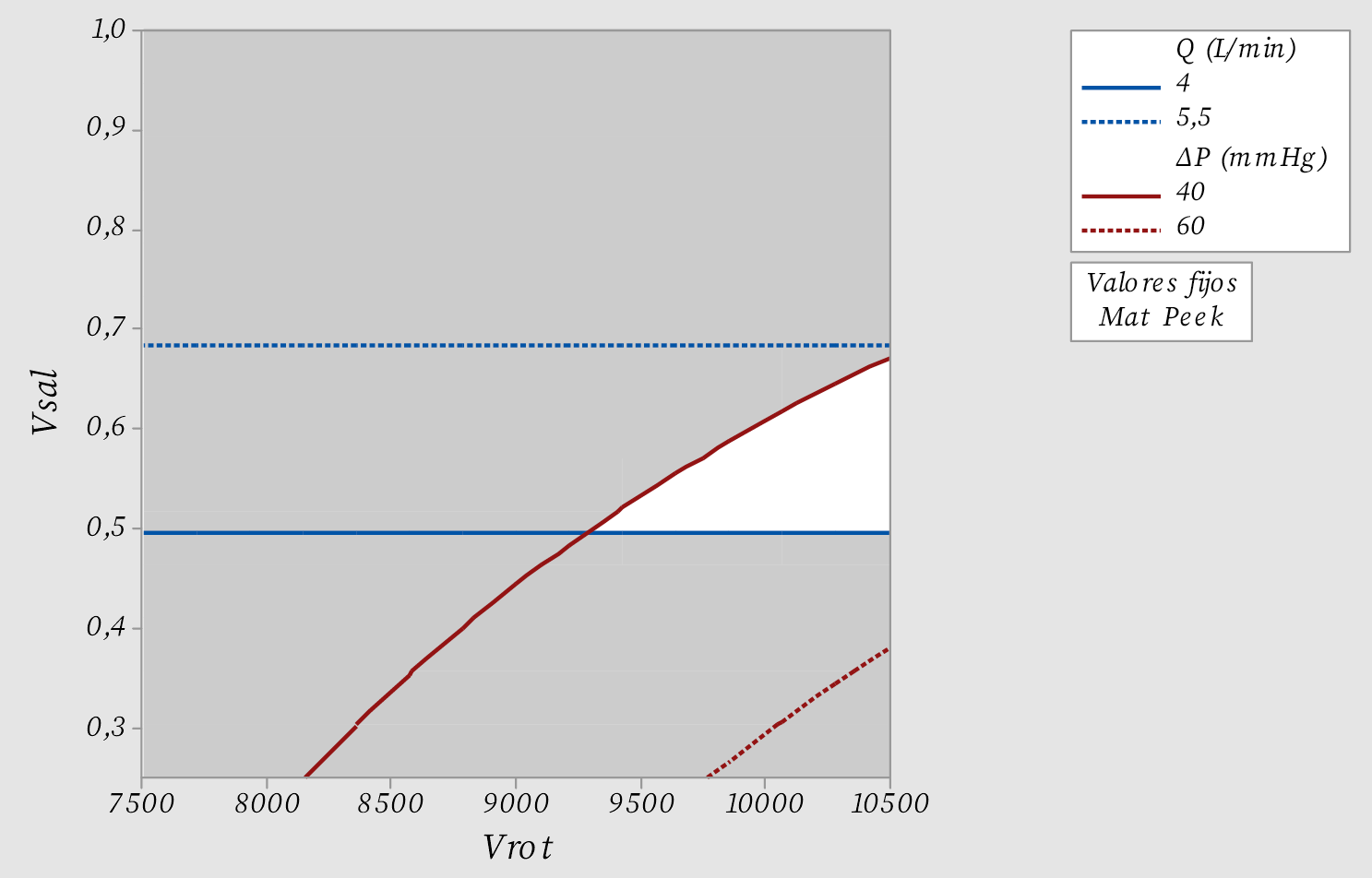
Figura 8. Gráfica superpuesta de contornos para las respuestas Q y ΔP.
Por último, se realiza la optimización del punto de operación del impulsor agregando una importancia mayor para las respuestas de caudal y diferencia de presión, mientras que a la respuesta de deformación volumétrica se le asigna una importancia menor. Para el caudal se definen dos especificaciones de 4 L/min y 5,5 L/min junto a la especificación de la diferencia de presión en 40 mmHg y la minimización de la deformación volumétrica. Los resultados se muestran en las figuras 9 y 10 donde se define la deseabilidad compuesta obtenida.
Para el caso presentado en la figura 9 de un caudal de 4 L/min y una diferencia de presión de 40 mmHg, la respuesta se optimiza para una velocidad de rotación de 9 258 rpm y una velocidad de salida de 0,4965 m/s. La diferencia entre el Platino y el Peek se genera principalmente con el valor obtenido para la deformación volumétrica, lo que produce una deseabilidad compuesta de 0,9987 para el Platino y de 0,8007 para el Peek.
En la figura 10 las especificaciones son de 5,5 L/min para el caudal y 40 mmHg para la diferencia de presión. La optimización de la respuesta se consigue con un valor de velocidad de rotación de 10 500 rpm y una velocidad de salida de 0,6827 m/s. De igual manera, la diferencia en la deseabilidad compuesta se debe a la respuesta de la deformación volumétrica. Para el Platino se obtiene un valor de 0,9909 y en el Peek un valor de 0,6690.
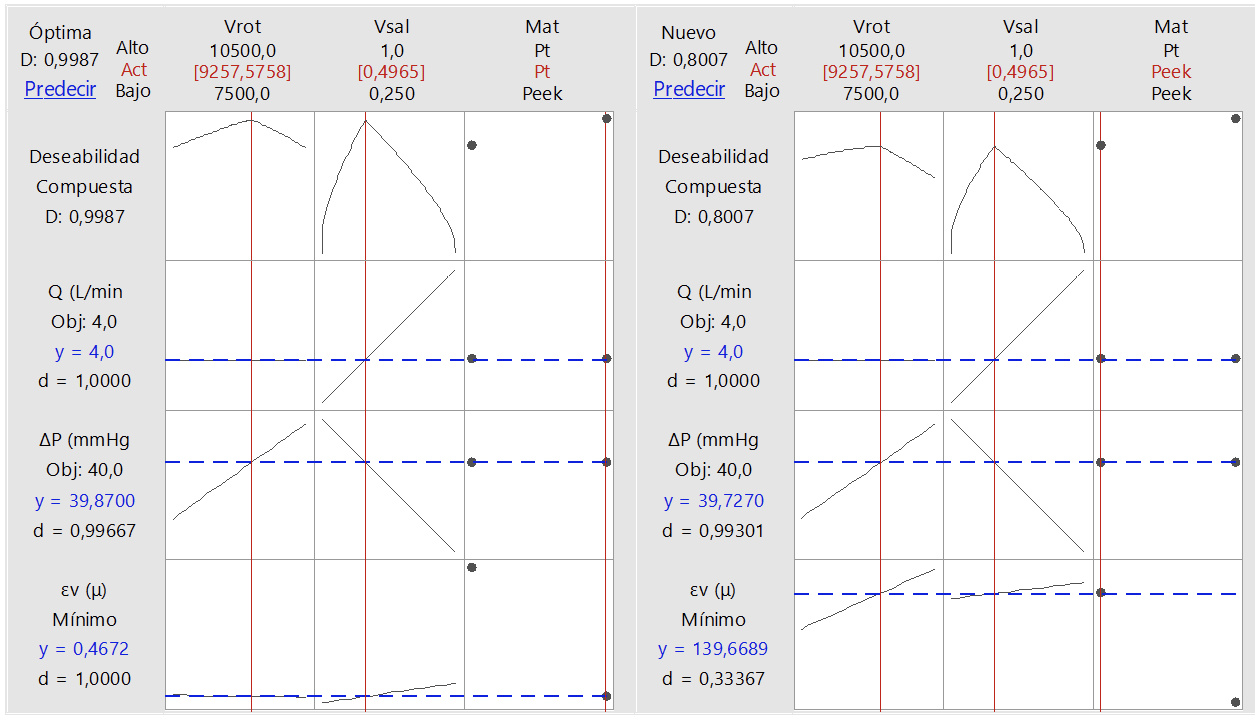
Figura 9. Gráficas de optimización para Q = 4 L/min, ΔP = 40 mmHg y εv mínimo.
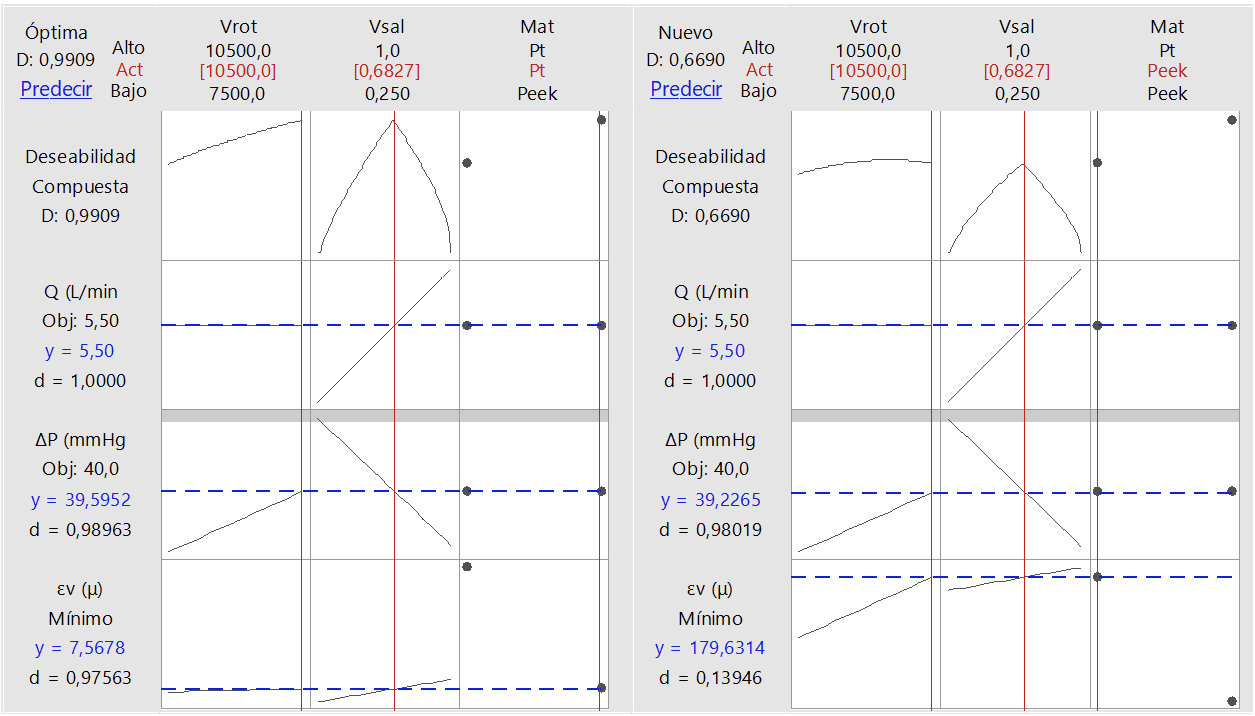
Figura 10. Gráficas de optimización para Q = 5,5 L/min, ΔP = 40 mmHg y εv mínimo.
Conclusiones y recomendaciones
Se define que el punto de operación óptimo para conseguir un caudal de 4 L/min y una diferencia de presión de 40 mmHg entre la entrada y la salida del impulsor axial sin eje central corresponde a una velocidad de rotación de 9 258 rpm y una velocidad de salida del flujo sanguíneo de 0,4965 m/s. Para cumplir con el requerimiento de la diferencia de presión mínima se requiere una velocidad de rotación superior a 9 273 rpm y una velocidad de salida mínima de 0,4962 m/s. Se recomienda que nuevos estudios realizados para el impulsor se concentren en la zona y puntos de operación obtenidos.
En el caso de las ecuaciones de regresión para las distintas respuestas, se obtiene una relación lineal entre el caudal y la velocidad de salida, dicho valor constante proviene de la sección transversal del conducto por donde fluye la sangre. En la respuesta de la deformación volumétrica los factores velocidad de rotación, material y su interacción doble son los más significativos estadísticamente. Para la respuesta de la diferencia de presión los factores que predominan en el modelo son la velocidad de rotación, la velocidad de salida y su interacción doble.
Se logra aumentar los grados de libertad para el cálculo del error al agregar los puntos centrales en la matriz de diseño del experimento. Al tratarse de resultados provenientes de simulaciones, en caso de requerir repeticiones completas del experimento se recomienda variar las características físicas de los materiales en un porcentaje similar a las variaciones de materiales comerciales. De esta forma, cada repetición se podría realizar con un conjunto de parámetros que corresponden a una muestra de material distinta.
Debido a que se plantea sustituir el Platino por un material polimérico se recomienda realizar el estudio con otros materiales poliméricos biocompatibles que sean aptos para la fabricación del impulsor. Esto podría facilitar la depuración del modelo matemático obtenido. De igual forma, se recomienda un análisis similar en las etapas posteriores de la investigación cuando se obtengan resultados provenientes de una planta que simule el comportamiento del sistema a nivel físico.
Referencias
[1] Organización Mundial de la Salud, “Enfermedades transmisibles y análisis de salud: Situación de salud en las Américas: Indicadores Básicos 2017”, Washington, D.C., Estados Unidos.
[2] M. A. Siman, J. Watson, J. T. Baldwin, W. R. Wagner, and H. S. Borovetz, “Current and future considerations in the use of mechanical circulatory support devices”, Annu. Rev. Biomed. Eng., vol. 10, núm. 1, pp. 59–84, Ago. 2008, doi: 10.1146/annurev.bioeng.9.060906.151856.
[3] M. Hosseinipour, R. Gupta, M. Bonnell, and M. Elahinia, “Rotary mechanical circulatory support systems”, J. Rehabil. Assist. Technol. Eng., vol. 4, p. 205566831772599, Jan. 2017, doi: 10.1177/2055668317725994.
[4] L. W. Miller et al., “Use of a continuous-flow device in patients awaiting heart transplantation”, N. Engl. J. Med., vol. 357, núm. 9, pp. 885–896, Ago. 2007, doi: 10.1056/NEJMoa067758.
[5] J. G. Rogers, et al., “Intrapericardial left ventricular assist device for advanced heart failure”, N. Engl. J. Med., vol. 376, no. 5, pp. 451–460, Feb. 2017, doi: 10.1056/NEJMoa1602954.
[6] G. Ortiz, “Modelo de un nuevo concepto de impulsor para la aplicación en bombas para sangre”, Tesis de Doctorado, Instituto Tecnológico de Costa Rica, 2017.
[7] C. Mayorga, “Determinación computacional del comportamiento fluido-estructura de un impulsor en flujo sanguíneo”, Tesis de Maestría, Instituto Tecnológico de Costa Rica, 2018.
[8] J. Muñoz, “Determinación computacional de la fatiga en un impulsor axial sin eje central en flujo sanguíneo”, Tesis de Maestría, Instituto Tecnológico de Costa Rica, 2021.
[9] V. Jagota, A. P. S. Sethi, and K. Kumar, “Finite element method: An overview”, Walailak Journal of Science and Technology, vol. 10, núm. 1. pp. 1–8, Feb. 2013, doi: 10.2004/wjst.v10i1.499.
[10] R. C. Hibbeler, “Mechanics of materials”, 9th ed, NJ, USA: Pearson Education, 2014.
[11] A. Bedford, and K. Liechti, “Mechanics of materials”, 2nd ed, Switzerland: Springer Nature, 2020.
[12] H. Gutiérrez Pulido, and R. de la Vara Salazar, “Análisis y diseño de experimentos”, 3rd ed, México: McGraw-Hill, 2012.
[13] D. Montgomery, “Diseño y análisis de experimentos”, 8th ed, USA: John Wiley & Sons, 2013.
[14] R. Hernández, C. Fernández, and P. Baptista, “Metodología de la investigación”, 6th ed, México: McGraw-Hill, 2014.
[15] K. J. Bathe, H. Zhang, and S. Ji, “Finite element analysis of fluid flows fully coupled with structural interactions,” Comput. Struct., vol. 72, no. 1–3, pp. 1–16, Jul. 1999, doi: 10.1016/S0045-7949(99)00042-5.
[16] J. C. Pedro, and P. Sibanda, “An Algorithm for the Strong-Coupling of the Fluid-Structure Interaction Using a Staggered Approach,” ISRN Appl. Math., vol. 2012, pp. 1–14, Jun. 2012, doi: 10.5402/2012/391974.
[17] M. R. Hasniyati, H. Zuhailawati, and S. Ramakrishnan, “A Statistical Prediction of Multiple Responses Using Overlaid Contour Plot on Hydroxyapatite Coated Magnesium via Cold Spray Deposition,” Procedia Chem., vol. 19, pp. 181–188, Jan. 2016, doi: 10.1016/J.PROCHE.2016.03.091.
1 Maestría en Ingeniería en Dispositivos Médicos, Escuela de Ciencia e Ingeniería de los Materiales, Instituto Tecnológico de Costa Rica. Costa Rica. Correo electrónico: jvmunoz@itcr.ac.cr https://orcid.org/0000-0003-1778-414X
https://orcid.org/0000-0003-1778-414X