Estudio comparativo mediante diferentes métodos para el cálculo de tensiones de contacto en engranajes rectos

Comparative study using different methods for calculating contact tensions in spur gears

Yoan Manuel Ramos-Botello1, Mario Luís Fernández-Tamayo2, Jorge Alexander Bosch-Cabrera3 ,Santiago Amaury Santana-Reyes4, René Misael Arias-Hidalgo5

Fecha de recepción: 10 de junio de 2021
Fecha de aprobación: 6 de octubre de 2021

Ramos-Botello, Y.M; Fernández-Tamayo, M.L; Bosch-Cabrera, J.A; Santana-Reyes, S.A; Arias-Hidalgo, R.M. Estudio comparativo mediante diferentes métodos para el cálculo de tensiones de contacto en engranajes rectos. Tecnología en Marcha. Vol. 35-3. Julio-Setiembre 2022. Pág. 3-15.

https://doi.org/10.18845/tm.v35i3.5611

Palabras clave

Engranaje; elementos finitos; fatiga superficial; criterio de Hertz; tensiones de contacto.

Resumen

Una de las causas de fallo que con mayor frecuencia se presentan en las transmisiones por engranajes, es la conocida como fatiga superficial o picadura. Para predecir el comportamiento del material frente a este fenómeno, las normas internacionales de diseño, Asociación Americana de Manufactura de Engranajes (AGMA) y la Organización Internacional para la Normalización (ISO), formulan modelos basados en la distribución de presiones de Hertz, para el contacto entre sólidos. En esta investigación se comparan las tensiones de contacto en engranajes cilíndricos de dientes rectos, de acuerdo a lo planteado por las normas antes mencionadas, el criterio de Hertz y mediante el método de elementos finitos. Los modelos en tres dimensiones fueron obtenidos con la ayuda de un paquete de diseño asistido por computadora (CAD), donde se tuvieron en cuenta las especificaciones de cada norma. Como una de las variantes de cálculo a comparar, es el resultado obtenido por simulación numérica, solo se tendrán en cuenta los factores que dependan de la geometría del diente y el material del mismo. Los resultados obtenidos se analizaron estadísticamente, donde se determinó la efectividad del método de elementos finitos para este tipo de cálculo, además, estos se asemejan más a los obtenidos por método de Hertz que es la teoría que sirve como base a las normas antes mencionadas.

Keywords

Gear; finite elements; surface fatigue; Hertz criteria; contact stresses.

Abstract

One of the most common causes of failure in gear drives is known as surface fatigue or pitting. To predict the behaviour of the material against this phenomenon, international design standards, the American Gear Manufacturing Association (AGMA) and the International Organization for Standardization (ISO), formulate models based on the Hertz pressure distribution, for the contact between solids. In this research, contact stresses are compared in straight-tooth cylindrical gears, in accordance with the provisions of the aforementioned standards, the Hertz criterion and through the finite element method.

The three-dimensional models were obtained with the help of a computer-aided design (CAD) package, where the specifications of each standard were taken into account. As one of the calculation variants to compare, it is the result obtained by numerical simulation, only the factors that depend of the tooth geometry and its material will be taken into account. The results obtained were analyzed statistically, where the effectiveness of the finite element method for this type of calculation was determined, in addition, these are more similar to those obtained by the Hertz method, which is the theory that serves as the basis for the aforementioned standards.

Introducción

Las fallas principales en la superficie de los dientes de los engranajes, están asociadas a la fatiga, como consecuencia de la acción repetida de carga y descarga de dichos dientes durante el funcionamiento del par engranado. El estudio a fatiga no es una ciencia exacta y absoluta, de la cual pueden obtenerse resultados exactos, sino que es un estudio aproximado y relativo [1, 2]. En los engranes este fenómeno no se ha comprendido por completo y es evidente que el estudio de este problema es mucho más complejo que el análisis de falla por flexión [3]. Los métodos tradicionales de cálculo basados en criterios simplificados, no dan resultados adecuados en el análisis de situaciones complicadas, de manera que deben de ser aceptadas suposiciones y simplificaciones para que las soluciones pueden ser obtenidas mediante el cálculo manual. El desarrollo de procedimientos establecidos para el diseño de engranajes ha permitido la elaboración de un conjunto de normas, entre las que se destacan la American Gear Manufacturers Association (AGMA) y la International Organization for Standardization (ISO), aplicables a la construcción, control, explotación y cálculo de la capacidad de carga de engranajes. Para predecir el comportamiento del material en la zona de contacto entre los dientes, dichas normas formulan modelos basados en la distribución de presiones de contacto de Hertz para el contacto entre sólidos [4]. En engranes cilíndricos de diente rectos, los puntos donde las normas antes mencionadas localizan las tensiones máximas de contacto no coinciden. Mientras la ISO considera como punto crítico el punto de rodadura y la AGMA toma el punto de contacto único inferior del piñón, que no coincide con el de rodadura más que en casos auténticamente singulares. Aunque ambas normas se basan en el modelo de Hertz, ninguna de estas coincide con el punto teórico de máxima presión superficial que predice dicho modelo [5, 6]. Por otra parte, el Método de los Elementos Finitos (MEF), parece ser una alternativa más para el cálculo de las tensiones de contacto en engranajes. No obstante, presenta limitaciones, pues muchos de los factores tenidos en cuenta de forma analítica, en el MEF no se pueden considerar. Esta investigación tiene como objetivo comparar las tensiones de contacto en engranajes cilíndricos de dientes rectos, de acuerdo a lo planteado por las normas antes mencionadas, por el criterio de Hertz y los resultados obtenidos mediante elementos finitos. Para ello se analizan diez casos de estudio y los resultados se analizarán estadísticamente. Se calcularán los valores de tensiones en el punto de contacto a partir de diferentes métodos:

•Tensiones de Hertz según los parámetros geométricos del engrane establecido por la norma ISO (ISO Hertz).

•Tensiones de Hertz según los parámetros geométricos del engrane establecido por la norma AGMA (AGMA Hertz).

•Tensiones de contacto a partir de la ISO (ISO).

•Tensiones de contacto a partir de la AGMA (AGMA).

•Tensiones de contacto a partir del MEF según lo planteado por la norma ISO (ISO MEF).

•Tensiones de contacto a partir del MEF según lo planteado por la norma AGMA (AGMA MEF).

Materiales y métodos

Cálculo analítico de los esfuerzos de contacto

El fundamento del cálculo analítico del esfuerzo de contacto se basa en la denominada presión de Hertz que estudia el fenómeno de los esfuerzos que surgen entre dos esferas en contacto bajo una fuerza aplicada. Posteriormente se particularizó dicha teoría para otros casos como el del contacto entre dos cilindros de una longitud determinada. Es en esta teoría en la que se basan los estudios desarrollados por las normas ISO y AGMA para el cálculo de las tensiones de contacto en los flancos de los dientes de los engranes [7, 8].

Esfuerzo de contacto en dos cilindros según Hertz

Cuando dos cilindros macizos de diámetros D1 y D2 se presionan entre sí bajo la acción de una fuerza (Fn), se obtiene un área de contacto de forma rectangular igual a dos veces el semiancho del área de contacto (B), la cual se forma por la deformación de las partes en contacto (figura 1). Esta variable se determina según la ecuación (1). Teniendo en cuenta esta variable, la fuerza y la longitud de contacto (lc), es posible determinar la presión máxima de contacto (Pmáx) en la zona deformada según se plantea en la ecuación (2) [9, 10].

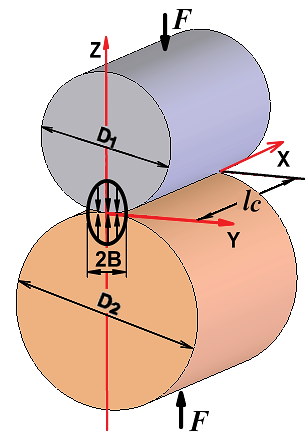
Figura 1. Cilindros en contacto bajo la acción de la fuerza F.

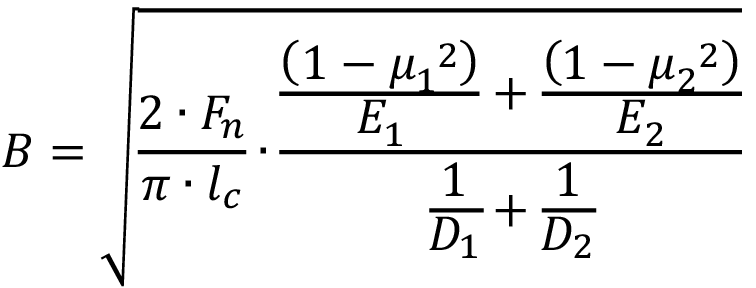(1)

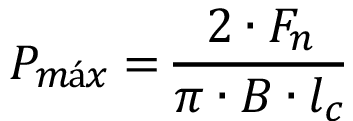(2)

Donde µ1, µ2, E1, E2 corresponden a los coeficientes de Poisson y módulos elásticos respectivamente de los materiales.

Bajo estas condiciones se producen tensiones en las tres direcciones principales (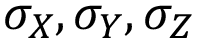), pero para este estudio se tomará solo el valor máximo que es cuando una de estas coincide con el valor de 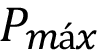(ecuación 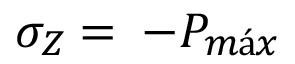3).

(3)

El punto de contacto entre los engranajes de diente recto se puede considerar como la zona de contacto entre dos cilindros. En el caso de dichos engranajes, surgen la fuerza normal (Fn), la cual se descompone en la radial (Fr), tangencial (Ft) (figura 2). En el caso de la teoría de Hertz la fuerza a utilizar es Fn mientras las normas ISO y AGMA para el cálculo de los esfuerzos de contacto la fuerza utilizada es Ft [11, 12].

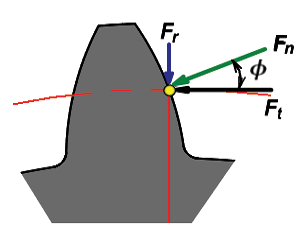
Figura 2. Fuerzas sobre un diente del engranaje.

Esfuerzos de contacto según las normas ISO y AGMA

Debido a que en la simulación por elementos finitos solo se trabaja con un modelo geométrico ideal, (sin errores de fabricación y montaje), no se tendrán en cuenta en las expresiones de cálculo de las normas ISO y AGMA, los factores que hacen referencia a estos errores, como tampoco los que hacen referencia a la sobrecarga dinámicos de la transmisión. Estas simplificaciones son para que haya igualdad de condiciones entre lo planteado por las normas antes mencionadas y la simulación numérica. Dichas simplificaciones solo tienen valor desde el punto vista teórico, ya que desde el práctico es imprescindible tener en cuenta cada factor. No obstante, estas simplificaciones son necesarias para comparar los resultados según los métodos objeto de estudio ya que así, se consideran los mismos parámetros, por lo cual se pueden comparar los resultados.

Por ello solo se incluirán en las ecuaciones los factores que hacen referencia únicamente a la geometría de la transmisión. Esto se debe fundamentalmente a:

•El modelo geométrico utilizado para la simulación por el método de los elementos finitos, tiene los dientes del engranaje con el perfil ideal (sin errores de fabricación y montaje).

•Se analizan algunos dientes del engranaje, no el montaje de la transmisión completa.

•No se considera la lubricación.

Estas simplificaciones son para poder comparar los resultados teóricos con los obtenidos a partir de la simulación numérica. Teniendo en cuenta lo antes planteado, las ecuaciones para determinar las tensiones de contacto, en engranes rectos de perfil evolvente según las normas ISO y AGMA quedarán tal como se muestran en las ecuaciones 4 y 5 respectivamente.

Según las normas ISO.

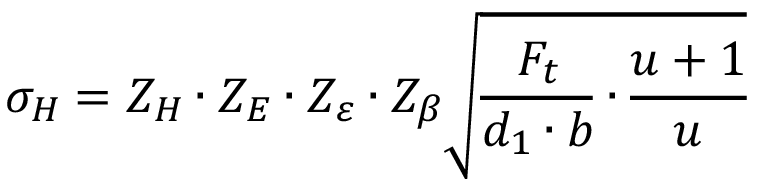(4)

Según las normas AGMA.

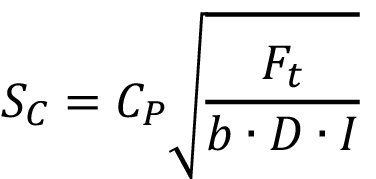(5)

Donde 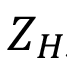, , 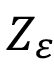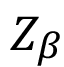son los coeficientes de zona, de recubrimiento y de ángulo de hélice respectivamente. La variable b es el ancho del engrane el cual se considerará igual a lc. ZE y CP consideran la influencia de las propiedades elásticas del material de los dientes del piñón y el engrane y tendrán el mismo valor. Finalmente las variables u, d1, D, e I son la relación de transmisión, diámetro primitivo, diámetro de paso y el factor de geometría respectivamente.

Punto de aplicación de la presión de contacto en los engranes

Para el cálculo por elementos finitos es necesario determinar las zonas del perfil del diente donde se aplicarán las cargas. Según plantea la ISO, esto sucede en el punto de rodadura, o sea, a una distancia del centro del piñón igual a 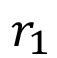(ecuación 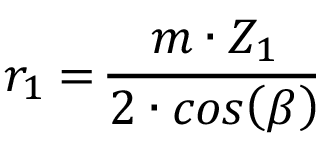6).

(6)

Siendo m y Z1 el módulo y número de dientes del piñón respectivamente. El ángulo β en este caso es igual a 0o.

Por su parte la AGMA plantea que los máximos esfuerzos de contacto suceden en el punto de contacto único inferior del piñón, situado a una distancia del centro de dicho piñón 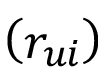(ecuación 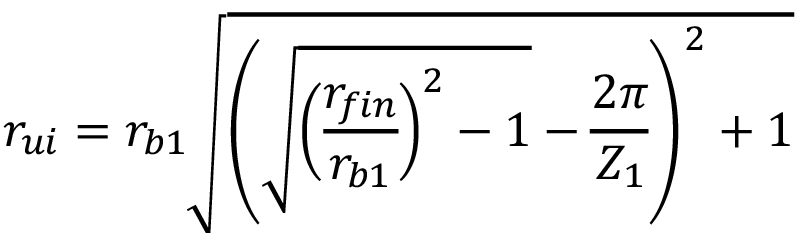7).

(7)

Donde 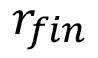es el radio de finalización de engrane, 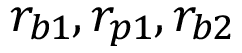son los radios base y primitivos del piñón y la rueda respectivamente. Una vez determinada las distancias del centro del engrane hasta el punto de aplicación de la carga según la norma correspondiente, es posible delimitar la zona de aplicación de la carga, la cual tendrá forma rectangular con un ancho igual a 2 B según lo establecido por Hertz (ecuación 1), mientras que la longitud coincide con el ancho del engrane (figura 3).

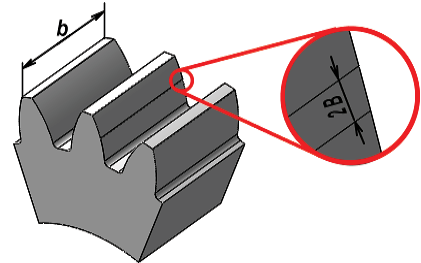
Figura 3. Zona de aplicación de la carga.

De acuerdo a las características del perfil evolvente de los dientes de los engranes, el punto de contacto entre dichos dientes se puede considerar como dos cilindros en contacto, por lo que es aplicable la teoría de Hertz. Para ello sería preciso conocer los diámetros D1 y D2 de estos cilindros en el punto de contacto, de acuerdo a las dos normas estudiadas (ecuaciones 8 y 9). Existen ligeras diferencias entre los resultados del cálculo de dichos diámetros, debido a la forma de calcular las distintas variables presentes en las ecuaciones 8 y 9 de acuerdo a las normas objeto de estudio. Los resultados obtenidos se utilizan en la ecuación 1 para determinar el semiancho del área de contacto.

(8)

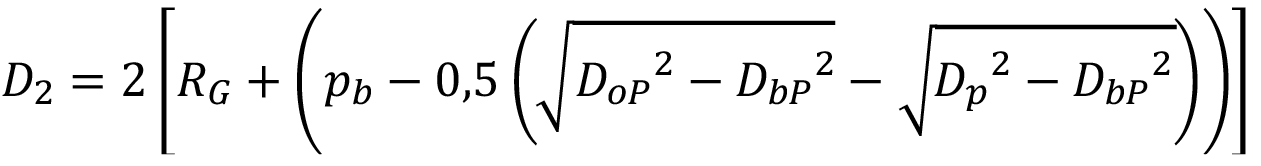(9)

Donde RP, RG son los radios de curvatura del piñón y el engrane respectivamente, mientras que DoP, DbP y Dp son los diámetros exteriores, de base y de paso del piñón respectivamente y 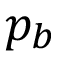es el paso base.

Consideraciones para los estudios

Para realizar los cálculos y el posterior análisis de los resultados, se fijaron determinados parámetros, los cuales se tendrán en cuenta para cada variante. Se calcularon 10 variantes las cuales se obtuvieron de la combinación de piñones de 18 y 25 dientes con 5 valores de módulos (m) según la norma ISO y los pasos diametrales equivalentes (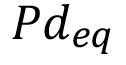) según la AGMA, de los cuales se obtuvo el valor normalizado (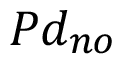) (cuadro 1). El ancho de dichos piñones es 48 mm al igual que los cilindros para el caso de la teoría de Hertz.

Cuadro 1. Parámetros que invariantes para cada caso de estudio.

No	m (mm)	Pdequiv (in-1)	Pdnorm (in-1)	Z1	Z2	b = lc (mm)	Cp = ZE (MPa1/2)
1	1	25,4	24	18	31	48	190,653
2	1	25,4	24	25	31	48	190,653
3	2	12,7	12	18	31	48	190,653
4	2	12,7	12	25	31	48	190,653
5	3	8,46	8	18	31	48	190,653
6	3	8,46	8	25	31	48	190,653
7	4	6,35	6	18	31	48	190,653
8	4	6,35	6	25	31	48	190,653
9	5	5,08	5	18	31	48	190,653
10	5	5,08	5	25	31	48	190,653

Cargas y restricciones

Para la aplicación de la carga a la cual se verán sometidas todas la variantes, se consideró un valor de momento torsor MT de 47,746 N m a partir del cual y conjuntamente con los parámetros geométricos de los engrane a calcular, se determinaron los valores de las fuerzas Ft y Fn. En los cuadros 2 y 3 se muestran los valores de estas fuerzas así como los valores de B y Pmáx para cada variante a calcular según lo planteado por la teoría de Hertz y las normas ISO y AGMA.

Cuadro 2. Parámetros según la ISO.

No	m (mm)	Z	r1 (m)	B (m)	Ft (N)	Fn (N)	Pmáx (MPa)
1	1	18	0,0090	5,006∙10-5	5305,162	5645,636	1495,7
2	1	25	0,0125	4,790∙10-5	3819,717	4064,858	1125,4
3	2	18	0,0180	5,006∙10-5	2652,581	2822,818	747,8
4	2	25	0,0250	4,790∙10-5	1909,858	2032,429	562,7
5	3	18	0,0270	5,006∙10-5	1768,387	1881,879	498,5
6	3	25	0,0375	4,790∙10-5	1273,239	1354,953	375,1
7	4	18	0,0360	5,006∙10-5	1326,291	1411,409	373,9
8	4	25	0,0500	4,790∙10-5	954,9292	1016,214	281,3
9	5	18	0,0450	5,006∙10-5	1061,032	1129,127	299,1
10	5	25	0,0625	4,790∙10-5	763,9434	812,9716	225

Cuadro 3. Parámetros según la AGMA.

No	m (mm)	Z	rui (m)	B (m)	Ft (N)	Fn (N)	Pmáx (MPa)
1	1	18	0,0092	5,15∙10-5	5305,162	5645,63	1453,9
2	1	25	0,0124	4,928∙10-5	3819,717	4064,857	1093,9
3	2	18	0,0185	5,15∙10-5	2652,581	2822,818	726,95
4	2	25	0,0249	4,928∙10-5	1909,858	2032,429	546,98
5	3	18	0,0278	5,15∙10-5	1768,387	1881,878	484,63
6	3	25	0,0374	4,928∙10-5	1273,239	1354,952	364,65
7	4	18	0,0371	5,15∙10-5	1326,290	1411,409	363,47
8	4	25	0,0499	4,928∙10-5	954,9292	1016,214	273,49
9	5	18	0,0445	5,046∙10-5	1061,032	1129,127	296,77
10	5	25	0,0599	4,828∙10-5	763,9434	812,9715	223,3

Para la simulacion numérica las cargas se aplicaron en las zonas del diente delimitada por dos veces el semiancho del área de contacto B establecido por Hertz (ecuación 1). Las distancias desde el centro del engrane al punto medio del área de aplicación de las cargas, se determina según lo planteado por las normas objeto de estudio y que se especifican en las ecuaciones 6 y 7 y los valores obtenidos para cada variante en los cuadros 2 y 3. Para simplificar el modelo de cálculo, se tomó una porción del engrane que incluye tres dientes, siendo en el diente central donde se aplicará la carga. Se eliminaron todos los grados de libertad del modelo aplicando restricciones en el cubo de la rueda y las caras laterales de la porción de engranaje (figura 4). Con esta simplificación se disminuye el tiempo de cálculo y no se compromete la calidad de los resultados obtenidos, ya que la zona del modelo a analizar se encuentra lo suficientemente alejada de los límites geométricos del modelo, como para que el estado tensional no se vea afectado por la cercanía de las restricciones de acuerdo al principio de Saint Venant. En investigaciones como las desarrolladas por [4, 12-14] también utilizan este tipo de simplificación obteniendo resultados satisfactorios, lo cual demuestran su efectividad.

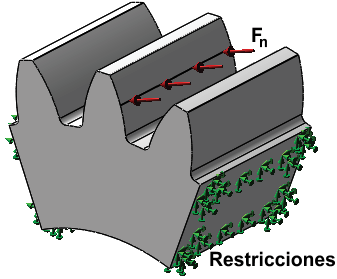
Figura 4. Cargas y restricciones.

Mallado de los modelos

En gran medida, la exactitud de los resultados depende de las características de la malla del modelo a calcular tal como plantea [7, 15, 16]. Por tal motivo para el mallado de los modelos se escogió un elemento finito sólido tetraédrico de alto orden (10 nodos), con tres grados de libertad por nodo. Para garantizar mayor precisión en los resultados, en la zona de aplicación de carga se utilizó una densidad de malla más fina que para el resto del modelo (figura 5), tal como plantea [12, 17]. Los modelos se mallaron con un tamaño de elementos de 4 mm mientras que el control de mallado se realizó con un tamaño de elemento de 0,05 mm. Para comprobar la calidad de la malla y con esto la de los resultados, se utilizó el método adaptativo p, el cual utiliza un orden de elemento progresivamente superior. Para los estudios, los resultados serán adecuados cuando la variación del valor de raíz cuadrada de las tensiones en nodos de von Mises es igual o menor al 0,5%.

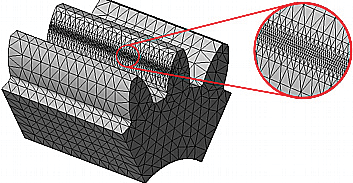
Figura 5. Mallado de los modelos.

Para los cálculos a realizar se consideró un acero AISI 4340 el cual es uno de los materiales utilizados para la fabricación de engranajes, por tener propiedades mecánicas acordes a las exigencias del destino de servicio de los mismos. En el cuadro 4 se muestran las propiedades mecánicas de dicho acero.

Cuadro 4. Propiedades mecánicas del acero AISI 4340 normalizado.

Propiedad	Valor	Unidad
Límite elástico	710	MPa
Límite de tracción	1110	MPa
Módulo elástico	200	GPa
Módulo cortante	78	GPa
Coeficiente de Poisson	0,29
Densidad	7850	kg (m3)-1

Fuente: [18].

Resultados

Una vez realizada la simulación numérica teniendo en cuenta los parámetros establecidos por las normas objeto de estudio (cuadros 2 y 3), se obtuvieron los valores de tensiones para cada variante propuesta. La variable que se tiene en cuenta para la comparación de los posteriores resultados fue la tensión de von Mises, coincidiendo esto con los estudios realizados por [4]. A continuación, se muestran los resultados para el primer caso de estudio (figura 6).

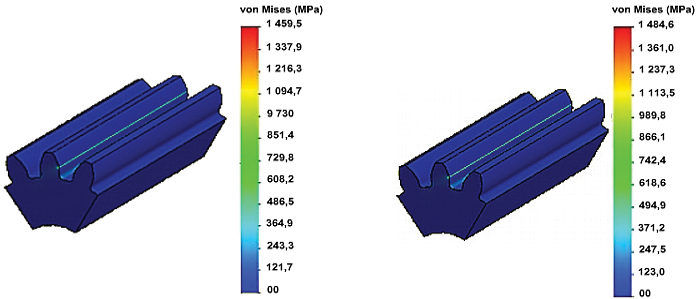
a) b)

Figura 6. Resultados del cálculo por elementos finitos para el primer caso de estudio. a) ISO MEF. b) AGMA MEF.

De forma similar se procedió a realizar el cálculo de cada variante a partir de los métodos establecidos en esta investigación. En el cuadro 5 se muestran los valores de tensiones obtenidos para cada variante según los parámetros correspondientes a cada caso y teniendo en cuenta los parámetros de cada norma.

Cuadro 5. Valores de tensiones de acuerdo a tres métodos deferentes, teniendo en cuenta los parámetros de las normas ISO y AGMA.

No	Según la ISO				Según la AGMA
	ISO Hertz (MPa)	ISO (MPa)	ISO MEF (MPa)		AGMA Hertz (MPa)	AGMA (MPa)	AGMA MEF (MPa)
1	1495,7	1484,8	1459,5		1453,9	1538,8	1484,6
2	1125,4	1142,9	1116,2		1093,9	1131,7	1114,06
3	747,8	742,4	736,5		726,95	769,4	741,2
4	562,7	571,4	565,3		546,98	565,8	542,6
5	498,5	494,9	486,8		484,63	512,9	486,7
6	375,1	380,9	379,09		364,65	377,2	371,7
7	373,9	371,2	369,5		363,47	384,7	362,3
8	281,3	285,7	284,1		273,49	282,9	278,5
9	299,1	296,9	286,08		296,77	314,1	289,4
10	225	228,5	223,8		223,3	231	222,7

A partir de los resultados obtenidos, se determinó las medias globales de cada caso de estudio (cuadro 6), observándose que el mayor valor corresponde a las tensiones según la norma AGMA.

Cuadro 6. Medias globales para cada caso de estudio.

Métodos de estudio	Media (MPa)
AGMA Hertz	582,804
AGMA MEF	589,370
ISO MEF	590,687
ISO Hertz	598,458
ISO	599,960
AGMA	610,850
Media global	595,355

Para poder comparar los resultados, se analizaron las diferencias entre las medias de los resultados de las tensiones calculadas por cada método, por lo que se aplicó un procedimiento de comparación múltiple para determinar las medias que son significativamente diferentes unas de otras. Estos resultados se exponen en la figura 6 y los valores obtenidos se muestran más detalladamente en el cuadro 7.

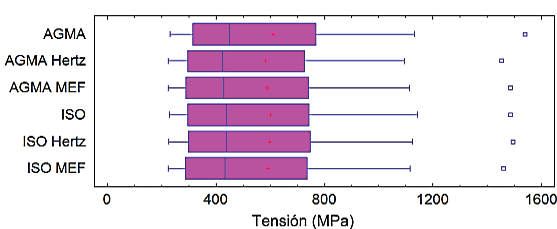
Figura 7. Comparación de los resultados.

Cuadro 7. Diferencias entre todos los métodos de cálculos.

Contraste	Diferencias (MPa)
AGMA MEF - ISO MEF	-1,31
ISO - ISO Hertz	1,50
AGMA Hertz - AGMA MEF	-6,56
ISO Hertz - ISO MEF	7,77
AGMA Hertz - ISO MEF	-7,88
AGMA MEF - ISO Hertz	-9,08
ISO - ISO MEF	9,27
AGMA MEF - ISO	-10,59
AGMA - ISO	10,89
AGMA - ISO Hertz	12,39
AGMA Hertz - ISO Hertz	-15,65
AGMA Hertz - ISO	-17,15
AGMA - ISO MEF	20,16
AGMA - AGMA MEF	21,48
AGMA - AGMA Hertz	28,04

Al analizar las diferencias entre las medias (cuadro 7), no se encontraron diferencias estadísticamente significativas entre ningún par de medias a un nivel de confianza de un 99,0 %. Esto demuestra que el método de los elementos finitos, puede ser una alternativa para el cálculo de las tensiones de contacto en engranajes cilíndricos de dientes rectos.

Se puede destacar que los resultados obtenidos entre la ISO – ISO Hertz tienen un mejor comportamiento que los de la AGMA – AGMA Hertz, lo cual demuestra que la norma ISO para el cálculo de tensiones de contacto, se asemeja más a lo planteado por Hertz que la norma AGMA. Los resultados por el método de los elementos finitos para las dos normas analizadas se asemejan más a los resultados obtenidos por Hertz, que es la teoría que sirve como base a las normas antes mencionadas. Por último, los resultados obtenidos por el método de los elementos finitos se acercan más a los de la norma ISO que los obtenidos por la AGMA.

Conclusiones

Al comparar los resultados obtenidos por los diferentes métodos de cálculo, no se encontraron diferencias estadísticamente significativas para un nivel de confianza de un 99 % lo cual pone de manifiesto la efectividad de cada método. Los resultados obtenidos de acuerdo a lo planteado por la norma ISO se asemeja más a los obtenidos a partir de la teoría de Hertz. En la investigación se demostró que la simulación numérica resulta ser una alternativa más para el cálculo de tensiones de contacto en engranes cilíndricos de diente recto, lo cual puede realizarse con un software de cálculo por elementos finitos. La principal limitación de este método está dado por las simplificaciones que hay que realizar, sin embargo se pueden obtener como resultado un gran número de variables como diferentes tipos de tenciones, deformaciones, desplazamientos que con los otros métodos se obtienen. Esto serviría para entender mejor el estado tensional al que se ve sometido un engrane durante su funcionamiento.

Referencias

[1] M. Jimenez-Martinez, “Manufacturing effects on fatigue strength,” Engineering Failure Analysis, vol. 108, p. 104339, 2020/01/01/ 2020. https://doi.org/10.1016/j.engfailanal.2019.104339

[2] R. Sun, C. Song, C. Zhu, X. Yang, and X. Li, “Computational study of pitting defect influence on mesh stiffness for straight beveloid gear,” Engineering Failure Analysis, vol. 119, p. 104971, 2021/01/01/ 2021. https://doi.org/10.1016/j.engfailanal.2020.104971

[3] H. Liu, H. Liu, C. Zhu, and J. Tang, “Study on gear contact fatigue failure competition mechanism considering tooth wear evolution,” Tribology International, vol. 147, p. 106277, 2020/07/01/ 2020. https://doi.org/10.1016/j.triboint.2020.106277

[4] S. S. Patil and S. Karuppanan, “Evaluation of the Effect of Friction in Gear Contact Stresses,” in Tribology in Materials and Applications, J. K. Katiyar, P. Ramkumar, T. V. V. L. N. Rao, and J. P. Davim, Eds. Cham: Springer International Publishing, 2020, pp. 227-242.

[5] Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth, 2016.

[6] Calculation of load capacity of spur and helical gears — Part 2: Calculation of surface durability (pitting), 2019.

[7] I. Gonzalez-Perez and A. Fuentes-Aznar, “Implementation of a finite element model for stress analysis of gear drives based on multi-point constraints,” Mechanism and Machine Theory, vol. 117, pp. 35-47, 2017/11/01/ 2017. https://doi.org/10.1016/j.mechmachtheory.2017.07.005

[8] M. B. Sánchez, M. Pleguezuelos, and J. I. Pedrero, “Approximate equations for the meshing stiffness and the load sharing ratio of spur gears including hertzian effects,” Mechanism and Machine Theory, vol. 109, pp. 231-249, 2017/03/01/ 2017. https://doi.org/10.1016/j.mechmachtheory.2016.11.014

[9] P. A. Gourgiotis, T. Zisis, A. E. Giannakopoulos, and H. G. Georgiadis, “The Hertz contact problem in couple-stress elasticity,” International Journal of Solids and Structures, vol. 168, pp. 228-237, 2019/08/15/ 2019. https://doi.org/10.1016/j.ijsolstr.2019.03.032

[10] V. L. Popov, Contact Mechanics and Friction, 2 ed. Springer, Berlin, Heidelberg, 2017.

[11] R. G. Budynas and J. K. Nisbett, Diseño en ingeniería mecánica de Shigley, 10 ed. México: McGraw-Hill, 2018.

[12] P. Sainsot and P. Velex, “On contact deflection and stiffness in spur and helical gears,” Mechanism and Machine Theory, vol. 154, p. 104049, 2020/12/01/ 2020. https://doi.org/10.1016/j.mechmachtheory.2020.104049

[13] T. J. Lisle, B. A. Shaw, and R. C. Frazer, “External spur gear root bending stress: A comparison of ISO 6336:2006, AGMA 2101-D04, ANSYS finite element analysis and strain gauge techniques,” Mechanism and Machine Theory, vol. 111, pp. 1-9, 2017/05/01/ 2017. https://doi.org/10.1016/j.mechmachtheory.2017.01.006

[14] R. Thirumurugan and N. Gnanasekar, “Influence of finite element model, load-sharing and load distribution on crack propagation path in spur gear drive,” Engineering Failure Analysis, vol. 110, p. 104383, 2020/03/01/ 2020. https://doi.org/10.1016/j.engfailanal.2020.104383

[15] W. Qu, H. Ding, and J. Tang, “An innovative semi-analytical determination approach to numerical loaded tooth contact analysis (NLTCA) for spiral bevel and hypoid gears,” Advances in Engineering Software, vol. 149, p. 102892, 2020/11/01/ 2020. https://doi.org/10.1016/j.advengsoft.2020.102892

[16] Y. M. Ramos , J. A. Bosch, A. Á. Álvarez, S. A. Santana, and R. M. Arias, “Cálculo por elementos finitos de las guías de un minitorno,” Revista Iberoamericana de Ingeniería Mecánica, vol. 24, no. 2, pp. 33-41, 2020.

[17] B. El Yousfi, A. Soualhi, K. Medjaher, and F. Guillet, “New approach for gear mesh stiffness evaluation of spur gears with surface defects,” Engineering Failure Analysis, vol. 116, p. 104740, 2020/10/01/ 2020. https://doi.org/10.1016/j.engfailanal.2020.104740

[18] MatWeb. (2020, 22 de enero). Database of material properties. Acero AISI 4340, normalizado. Available: http://www.matweb.com/search/DataSheet.aspx?MatGUID=4a3cfc1e1cfd451091e67d3f3b66bb80&ckck=1

---