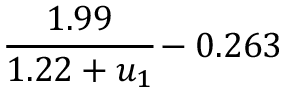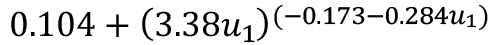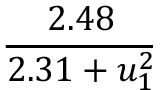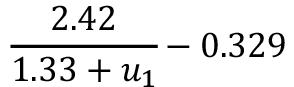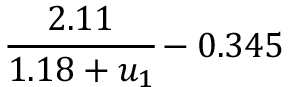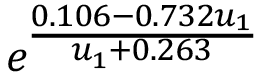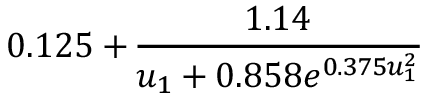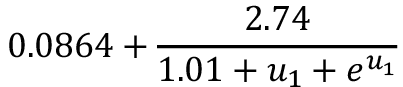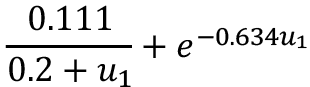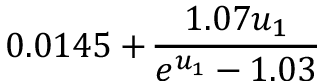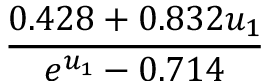Modelo dinámico de la velocidad del viento en una zona boscosa tropical

Dynamic model of wind speed in a tropical forested landscape

Gustavo Richmond-Navarro1, Gustavo Murillo-Zumbado2, Frank Marín-Guillén3, Pedro Casanova-Treto4

Fecha de recepción: 5 de abril de 2021
Fecha de aprobación: 6 de agosto de 2021

Richmond-Navarro, G; Murillo-Zumbado, G; Marín-Guillén, F; Casanova-Treto, P. Modelo dinámico de la velocidad del viento en una zona boscosa tropical5. Tecnología en Marcha. Vol. 35-2. Abril-Junio 2022. Pág 3-15.

https://doi.org/10.18845/tm.v35i2.5465

Palabras clave

Velocidad del viento; recurso eólico; longitud de rugosidad; zonas boscosas; modelo dinámico.

Resumen

Costa Rica establece en sus estrategias nacionales el desarrollo de energías renovables para disminuir la dependencia de los combustibles fósiles, la explotación del recurso eólico es una de las alternativas para este fin. Para maximizar este recurso es necesario entender la interacción del viento con el terreno, en especial en un país que el 52 % de cobertura corresponde a zona boscosa. Lograr encontrar un modelo dinámico que describa la conducta del viento y que considere la longitud de rugosidad como variable y no como una constante, como usualmente se utiliza en la literatura, es el objetivo de este trabajo. Para lograr esto se analizan series de tiempo de datos obtenidos de dos estaciones meteorológicas, administradas por el Instituto Tecnológico de Costa Rica (ITCR) y el Instituto Meteorológico Nacional (IMN), ambas estaciones ubicadas en el Campus de Cartago del ITCR, los datos corresponden a alturas sobre el suelo de 1.5 m y de 10 m. Se utiliza el software Eureqa para encontrar la relación de las distintas variables meteorológicas, tanto para la longitud de rugosidad como para la velocidad del viento. Se obtienen varias expresiones en distintos escenarios y se logra obtener un modelo para la velocidad del viento en el eje vertical, que sustituye el valor clásico de la longitud de rugosidad por una función, haciendo posible estimar el valor de la velocidad del viento en el eje vertical con mediciones en un punto cercano al suelo de modo que evita tener que instalar equipo costoso y grandes estructuras.

Keywords

Wind speed; wind resource; roughness length; forested landscape; dynamic model.

Abstract

Costa Rica has established the development of renewable energy sources as part of the strategy to diminish the fossil fuel dependency. The utilization of wind as a source of energy is one of the alternatives. To maximize the use of wind is necessary to understand the wind-landscape interaction, especially in a country where 52 % of the terrain is covered by forest. The aim of this paper is to find a dynamic model that describes the wind behaviour that considers the roughness length as a variable and not as a constant, as it is usually considered within the literature. A series of data obtained from two different weather stations are analysed. The weather stations are managed by two different institutions: Instituto Tecnológico de Costa Rica (Costa Rica Institute of Technology) and Instituto Meteorológico Nacional (Costa Rica Institute of Meteorology). Both weather stations are located at the main campus of Costa Rica Institute of Technology and data were obtained at two heights above ground level: 1.5 meters and 10 meters. Eureqa software was used to find a correlation between the different weather variables and roughness length as for wind speed. Several expressions are obtained in various scenarios as well as a model for wind speed that replaces the classic roughness length constant value with a dynamic expression, being able to estimate the wind speed at the vertical axis with data from a measuring height near to the ground, avoiding the investment in high value equipment and the necessity of installing support structures of considerable scale.

Introducción

Las fuentes de energía renovables son de particular interés para los países en vías de desarrollo [1]. A manera de ejemplo, una de las principales estrategias de la República de Costa Rica en su Plan Nacional de Energía 2015 – 2030, es disminuir la dependencia de combustibles fósiles [2], una alternativa que contribuye a alcanzar este tipo de objetivos es la explotación del recurso eólico.

El comportamiento del viento depende en gran medida de la composición de la superficie, siguiendo con el ejemplo de Costa Rica, su superficie está cubierta en un 52 % por zonas boscosas [3], lo cual es usual en los países tropicales. Por esta razón, es necesario comprender en detalle la interacción entre este tipo de terrenos y el viento, para aprovechar el recurso eólico en las zonas boscosas tropicales.

En la literatura existen múltiples modelos para el perfil de viento, por ejemplo, la Ley Logarítmica [4] mostrada en la ecuación 1, relaciona la magnitud de la velocidad del viento (u); con la altura sobre el suelo (z), el esfuerzo cortante superficial (t0), la densidad del aire (r), la longitud de rugosidad (z0) y la constante de Von Karman (k).

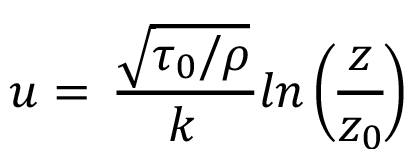(1)

La longitud de rugosidad se define como la altura sobre el suelo a la cual la velocidad es nula, depende principalmente de la vegetación y el tipo de terreno. Según el tipo de superficie varios autores han reportado valores para la longitud de rugosidad como se muestra en el cuadro 1, del cual destaca que, en terreno plano como hielo, la longitud de rugosidad es sumamente pequeña. También se puede apreciar que para superficies específicas existe una discrepancia notable cuando se comparan los valores reportados por los diferentes autores.

Cuadro 1. Valores de longitud de rugosidad para diferentes terrenos según varios autores.

Surface	ESDU (1972)	Troen and Lundtang Petersen (1989)	Wieringa (1992)	Fiedler according to Hasager and Jensen (1999)	Davenport et al. (2000)
Ice	10-5
Water	10-4 - 10 -3
Snow	0.002
Bare soil		0.03	0.004	0.03	0.005
Grassland	0.005-0.02	0.03	0.06	0.08	0.03
Winter crops (winter)		0.1	0.09	0.12	0.1
Winter crops	0.05	0.1	0.18	0.09	0.25
Summer crops	0.05	0.1	0.18	0.09	0.25
Clearings		0.1	0.35	0.004	0.2
Shrubs	0.3	0.4	0.45	0.3	0.5
Conifer forest	1-2	0.4	1.6	0.9	1.0
Deciduous forest	1-2	0.4	1.7	1.2	2.0
Settlement	0.5-2	0.4	0.7	0.5	2.0

Fuente: [5]

Una manera usual de emplear la Ley Logarítmica de la ecuación 1 es relacionar la velocidad del viento a dos diferentes alturas, de modo que se puede obtener la expresión mostrada en la ecuación 2 para la velocidad (u2) a una altura (z2), en función de la velocidad (u1) a una altura (z1) y de la longitud de rugosidad (z0) del sitio particular.

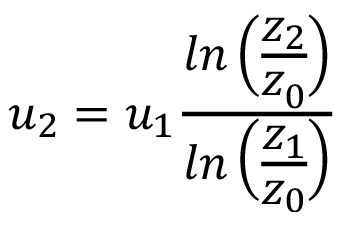(2)

La longitud de rugosidad puede ser despejada de la ecuación 2 para obtener la expresión que se presenta en la ecuación 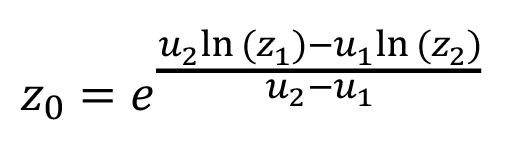3.

(3)

En presencia de obstáculos prominentes tales como árboles, la altura de la Ley Logarítmica debe ser reemplazada por la expresión (z - zd), tal como se muestra en la ecuación 4. El término (zd) es conocido como altura de desplazamiento del plano cero [6].

(4)

Considerando que tanto la longitud de rugosidad como la altura de desplazamiento del plano cero se deben al terreno, en el caso de la primera debido al tipo de vegetación y en el caso de la segunda debido a obstáculos más grandes, es posible conceptualizar la suma de ambas como el punto donde inicia el perfil de velocidad vertical, como se muestra en la figura 1.

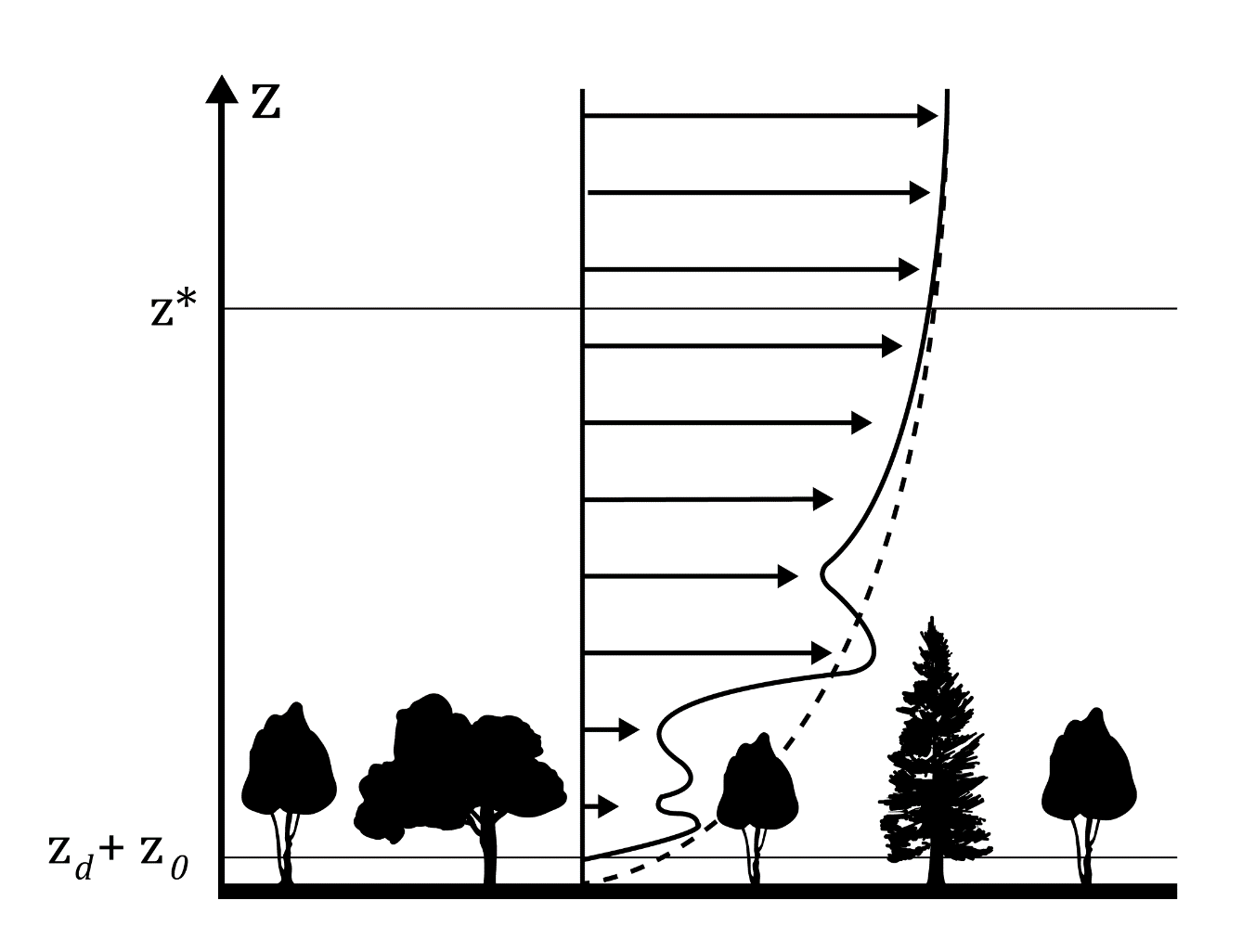
Figura 1. Perfil de viento vertical en una zona boscosa.

La altura mínima para la cual la ecuación 4 es válida, se identifica como (z*) en la figura 1 y se denomina altura de difusión de estela, la cual marca la división entre la sub capa rugosa (en inglés buffer layer, transition layer o roughness sublayer -RSL-) y la sub capa inercial (en inglés logatithmic layer). Autores como Mertens [7] indican valores de (z*) entre 34.5 y 39 m. A manera de referencia, en zonas urbanas (zd) puede tomarse como tres cuartos del promedio de la altura de las edificaciones [4].

Otro modelo para el perfil de viento es conocido como la Ley de Potencia y se muestra en la ecuación 5. En este caso se relaciona la velocidad del viento con una velocidad de referencia (uref) a una altura de referencia (zref) y existe un exponente (a) que depende de la rugosidad del terreno, así como del rango de alturas. Resultados experimentales [8] indican que usualmente (a) = 1/7.

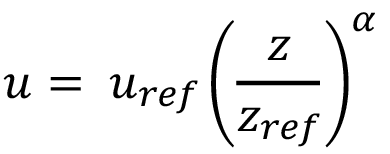(5)

Investigaciones en sitios específicos, que hacen uso de herramientas como redes neuronales, reportan modelos explícitos para (a) en función de la velocidad medida a una altura de referencia [9].

Existe una relación entre el exponente de la Ley de Potencia y la longitud de rugosidad de la Ley Logarítmica [4], como se muestra en la ecuación 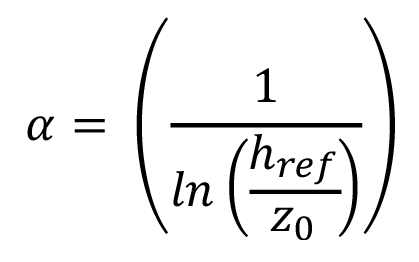6.

(6)

Donde (href) es la altura para la cual la ecuación 1 da el mismo resultado que la ecuación 5.

De los modelos presentados se extrae que la determinación de la longitud de rugosidad es fundamental para conocer el perfil de velocidad y estimar así el recurso eólico, sin embargo, distintas investigaciones señalan que la longitud de rugosidad es variable en muy distintos tipos de [10]-[12]. En el caso de [13] se analizan los efectos del cambio de la altura promedio de los árboles en la longitud de rugosidad y se encuentra que la relación entre estos términos es sumamente variable.

Por otra parte, para modelar el recurso eólico en general, más allá del perfil de velocidad, existen propuestas metodológicas para el mapeo mediante expresiones explícitas que consideran la forma y distribución de los obstáculos en el suelo [14], en sitios o regiones específicas, también modelos semi-empíricos que se alimentan de grandes cantidades de datos y diseñados específicamente para evaluar sitios de potencial para turbinas eólicas de pequeña escala [15]. Sin embargo, los métodos más usuales, requieren de la caracterización de la estructura completa del terreno, específicamente de la altura de los obstáculos como árboles en zonas boscosas [16], esto con herramientas muy avanzadas y costosas como mediciones láser conocidas como LiDAR (Del acrónimo en inglés Light Detection and Ranging) [17], o bien censado remoto en general [18], las cuales requieren de un alto costo de inversión.

Considerando la amplia variabilidad que existe en la literatura para el valor de (z0) y lo distintos que pueden ser sus valores para un bosque, como se indica en el cuadro 1, el objetivo de esta investigación es contribuir al modelamiento del recurso eólico en un área boscosa tropical, proponiendo una expresión para (z0) a partir de la velocidad del viento medida a una única altura, cercana al suelo, para con ello poder describir el perfil de velocidad con un modelo dinámico, que dependa de una expresión variable de la longitud de rugosidad, sin el uso de equipos de alto costo.

Metodología

En esta investigación se trabajó con dos conjuntos de datos de velocidad del viento, provenientes de diferentes fuentes, tomados en el mismo punto a 1.5 y 10 metros de altura sobre el nivel del suelo. Se realizó la asociación de los datos en función del tiempo, con lo que se construyó una tabla con la velocidad del viento a dos alturas para cada momento del tiempo.

Se calculó la longitud de rugosidad para cada pareja de datos, empleando la ecuación 3. Luego se procesaron los datos con el software de inteligencia artificial Eureqa, de Nutonian Inc., el cual permite encontrar una relación funcional entre las variables, usando una técnica de búsqueda evolutiva llamada regresión simbólica. En diferentes escenarios se buscó obtener la longitud de rugosidad como una función de la velocidad del viento medida a 1.5 m de altura, para finalmente reemplazar el valor de (z0) en la ecuación 3 y obtener una expresión dinámica para la velocidad del viento en el eje vertical en función únicamente de una velocidad y altura de referencia, siendo independiente de un valor fijo de longitud de rugosidad.

Descripción de los datos

Los datos abarcan del 31 de agosto de 2011 al 2 de mayo de 2017, las variables fueron registradas 1 vez por hora. El punto de medición está en las coordenadas 09°51’08” N, 83°54’31” O, a 1360 metros sobre el nivel del mar. Lo que corresponde a una zona boscosa tropical.

Las mediciones a 10 m de altura sobre el suelo fueron adquiridas con una estación meteorológica marca Campbell Scientific, cuyo anemómetro mide la magnitud de la velocidad del viento en un rango de 0 m/s a 50 m/s con una precisión de ± 0.5 m/s y un valor umbral de 0.5 m/s. Estos datos fueron facilitados a los autores por el Instituto Meteorológico Nacional, para fines únicamente de investigación.

Los datos a 1.5 metros sobre el suelo se tomaron con una estación meteorológica marca Davis, equipada con un anemómetro que mide magnitudes de la velocidad del viento en el rango de 0 m/s a 80 m/s con una precisión de ± 1 m/s, una resolución de 0.1 m/s y un valor umbral de 0.4 m/s. Estos datos fueron tomados directamente por personal del Instituto Tecnológico de Costa Rica.

En ambas alturas se emplearon anemómetros de copas para determinar la velocidad del viento.

Pre procesamiento de los datos con Microsoft Excel y Matlab

Al tener dos fuentes de información de dos estaciones de distintos fabricantes, se requirió un pre proceso de ordenamiento, identificación y filtrado para tener los datos del mismo momento de tiempo para las dos alturas. Esto se hizo con un código programado en Matlab en el cual también se eliminaron todas las entradas de tiempo calmo, es decir de 0 m/s.

Con el procesamiento de datos en Matlab se identificaron y eliminaron todos los pares de datos en los que la velocidad del viento a 1.5 m era mayor que a 10 m de altura. Pues esa condición no coincide con el modelo logarítmico en el cual se basa este estudio.

Luego se calculó el promedio simple de los datos y la desviación estándar, adicionalmente para cada momento del tiempo se calculó la longitud de rugosidad, empleando la ecuación 3.

El último paso en el pre procesamiento fue clasificar, en Microsoft Excel, los datos según su fecha como valores en el día o la noche y en estación seca o lluviosa. Se consideró el día en horario de 6 am a 5:59 pm. El resto es la noche. No se hace distinción alguna de los cambios en el horario de salida y puesta del sol en el punto de medición, a lo largo del año, pues al estar cerca del ecuador terrestre, estos cambios son despreciables. Por otro lado, la estación seca se consideró desde diciembre hasta abril y la lluviosa de mayo a noviembre.

Procesamiento de los datos mediante regresión simbólica

Una vez construida una tabla con las columnas: fecha, hora, estación (seca o lluviosa), horario (diurno/nocturno), velocidad del viento a 1.5 m de altura (m/s), velocidad del viento a 10 m de altura (m/s) y longitud de rugosidad (m), se exportaron las tablas de datos a Eureqa y se definió una búsqueda de una relación funcional expresada en la ecuación 7, donde (u1) se refiere a la velocidad del viento medida a 1.5 m de altura sobre el suelo.

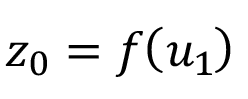(7)

Por la naturaleza del fenómeno, se incluyó entre los bloques de búsqueda de Eureqa las operaciones básicas: suma, resta, multiplicación y división; además de las operaciones más complejas como el exponencial, el logaritmo, raíces, potencias y factoriales. No se consideraron las funciones trigonométricas al ser conocido que el fenómeno no es oscilatorio, de acuerdo con los modelos encontrados en la literatura y presentados en la introducción.

Se realizaron nueve búsquedas de la relación funcional de la ecuación 7, considerando la segregación de datos que se muestra en el cuadro 2.

Cuadro 2. Conjuntos de datos seleccionados para cada búsqueda del modelo de la longitud de rugosidad.

Filtrado en los datos	Número de búsqueda	Codificación del modelo
Ninguno (Todos los datos son considerados)	1	Total
Horario diurno	2	Día
Horario nocturno	3	Noche
Estación seca	4	Seca
Estación lluviosa	5	Lluviosa
Horario diurno y estación seca	6	Día-Seca
Horario diurno y estación lluviosa	7	Día-Lluviosa
Horario nocturno y estación seca	8	Noche-Seca
Horario nocturno y estación lluviosa	9	Noche-Lluviosa

Se empleó la plataforma Windows Azure como recurso de computación en la nube, debido a la gran demanda de recursos que representa Eureqa, permitiendo correr el programa por varios días para cada búsqueda, sin comprometer los resultados por posibles interrupciones.

Para cada búsqueda del cuadro 2 se ejecutó Eureqa hasta lograr convergencia en el error absoluto medio en los modelos de regresión simbólica.

Análisis y resultados

Al calcular el promedio simple de todos los resultados puntuales de longitud de rugosidad, se obtiene que (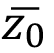) = 0.577 con una desviación estándar de 0.495, por lo cual, se ve la necesidad de un modelo para esta variable, considerando que la desviación es casi del tamaño del promedio. A la vez, se encuentra que los datos son consistentes con la literatura, pues al comparar el promedio obtenido con los valores del cuadro 1, se encuentra que el orden de magnitud para bosque es el correcto.

Los resultados se presentan en dos grupos, en primera instancia se muestran los modelos generales de longitud de rugosidad obtenidos según las nueve búsquedas descritas en la metodología.

Luego, a la luz de los resultados mismos, se repite el proceso de búsqueda acotando la función objetivo, eliminando el logaritmo natural, el factorial, la potencia y la raíz; conservando únicamente la función exponencial, junto con las operaciones básicas. Con esta iteración se obtienen los denominados modelos exponenciales.

Finalmente, se presenta la propuesta de modelo dinámico de velocidad del viento en función de la altura, para la zona boscosa tropical específica de este estudio.

Modelos generales para z0

Siguiendo la metodología, al correr Eureqa según las nueve búsquedas detalladas en el cuadro 2, se obtienen los nueve modelos que se detallan en el cuadro 3.

Cuadro 3. Modelos generales para la longitud de rugosidad.

Codificación del modelo	Modelo z0=	Coeficiente de correlación	Error absoluto promedio
Total		0.922	0.130
Día		0.832	0.130
Noche		0.887	0.131
Seca		0.896	0.109
Lluviosa		0.859	0.143
Día-Seca		0.808	0.102
Día-Lluviosa		0.828	0.139
Noche-Seca		0.826	0.114
Noche-Lluviosa		0.861	0.143

Considerando, por un lado, que los modelos ofrecen una amplia variabilidad de funciones y que el modelo con el total de los datos es el que posee un mayor coeficiente de correlación, sin sacrificar el error absoluto promedio; por otro lado, que el modelo Total tiene una estructura muy similar a la ecuación 3, se repite el proceso de búsqueda eliminando del motor de Eureqa las funciones logaritmo natural, factorial, potencia y la raíz. Con esto se obtienen los modelos exponenciales, que se detallan a continuación.

Modelos exponenciales z0

Al repetir el proceso de búsqueda funcional descrito en la metodología, pero eliminando las funciones logaritmo natural, factorial, potencia y la raíz, se obtienen los nueve modelos exponenciales mostrados en el cuadro 4.

Cuadro 4. Modelos exponenciales para la longitud de rugosidad.

Codificación del modelo	Modelo z0=	Coeficiente de correlación	Error absoluto promedio
Total		0.922	0.130
Día		0.832	0.129
Noche		0.887	0.131
Seca		0.896	0.110
Lluviosa		0.860	0.143
Día-Seca		0.811	0.102
Día-Lluviosa		0.829	0.138
Noche-Seca		0.909	0.114
Noche-Lluviosa		0.861	0.142

Con el objetivo de determinar si los modelos exponenciales representan una mejora respecto de los generales, se muestra en las gráficas 2 y 3 la comparación de los coeficientes de correlación y el error absoluto promedio para los modelos generales y exponenciales. En la figura 2 destaca que, en los modelos exponenciales, el coeficiente de correlación aumenta levemente respecto de los modelos generales. En la figura 3 se presenta una disminución del error absoluto promedio, por lo que se puede afirmar que los modelos exponenciales del cuadro 4 resultan más adecuados para describir el fenómeno. El modelo exponencial para la búsqueda 8, correspondiente a Noche-Seca, experimenta un aumento significativo en cuanto a coeficiente de correlación, respecto del modelo general. Esto sitúa al modelo Noche-Seca fuera de la tendencia, la cual es un ligero aumento en el coeficiente de correlación.

Como se evidencia en estos resultados, los modelos segregados tienen menor coeficiente de correlación que el modelo que contempla el total de los datos. Esto se debe a que al segregar los datos se pierde la continuidad del fenómeno en estudio, lo que genera una disminución en la correlación del modelo.

Por lo anterior, se opta por emplear un único modelo para todo momento del tiempo y para todas las posibles condiciones como día, noche, estación lluviosa o seca. Esto resulta particularmente conveniente pues permite describir la velocidad del viento sin tomar en cuenta parámetros adicionales.

Figura 2. Comparación del coeficiente de correlación entre los modelos generales y exponenciales.

Figura 3. Comparación del error absoluto promedio entre los modelos generales y exponenciales.

Modelo dinámico de la velocidad del viento

Considerando los resultados de los modelos exponenciales, se encuentra que la expresión para (z0) con mayor coeficiente de correlación es el modelo que considera todos los datos, lo que resulta conveniente pues una misma expresión puede emplearse para describir el fenómeno de velocidad del viento, en todo momento.

Si se toma la ecuación 2 y se reemplaza (z0) por la expresión obtenida en la búsqueda 1, se obtiene la ecuación 8, que permite calcular la velocidad del viento (u2) a una altura cualquiera (z2) en función de la velocidad del viento (u1) a una altura (z1), pero independiente de la longitud de rugosidad, para el sitio particular.

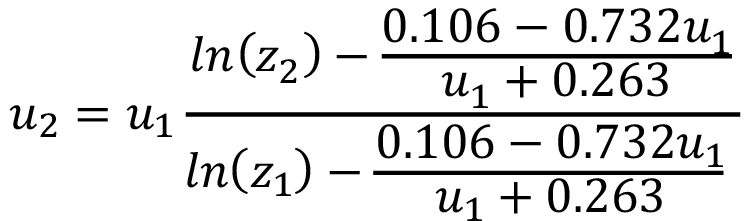(8)

La ecuación 8 se ha indicado como el modelo dinámico de la velocidad del viento, pues considera el valor de la longitud de rugosidad como una variable, que toma determinados valores en función de la propia velocidad del viento de referencia, es decir, el (z0) deja de ser una constante en esta propuesta y ahora es un valor dinámico.

Esta propuesta comprende de alguna manera los valores distintos que ofrece la literatura para la longitud de rugosidad.

Ahora bien, en el caso de los datos analizados, (z1) = 1.5 m y se han obtenido las constantes de la ecuación 8, pero de manera general, se puede plantear la ecuación 9, en función de tres parámetros a, b, c. Lo cual representa la posible aplicación de esta propuesta para otros escenarios, donde sería necesario determinar estos tres parámetros.

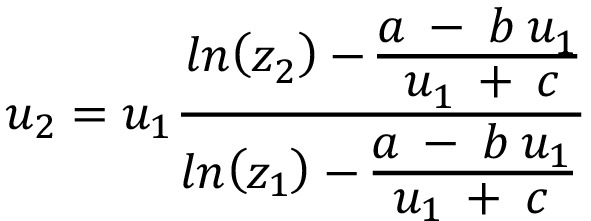(9)

Una comparación rápida de la ecuación 2 con la ecuación 9 haría pensar que se pasó de no conocer (z0) a no conocer tres parámetros, lo que a primera vista complicaría innecesariamente el análisis. Sin embargo, con esta formulación se ha reemplazado el valor constante de (z0) por un conjunto de parámetros que capturan la naturaleza variable de (z0), la cual ha sido identificado como tal en la literatura, por lo tanto, este procedimiento puede ser replicado en otras localidades para describir el perfil de velocidad de viento a baja altura.

Conclusiones

En esta investigación se desarrolló un modelo para la velocidad del viento en el eje vertical, sustituyendo el valor clásico de la longitud de rugosidad, por una expresión dinámica que depende de la velocidad del viento, lo cual captura el resultado de varias investigaciones que mencionan precisamente que el (z0) no es una constante.

El modelo propuesto en la ecuación 9 es válido para todas las estaciones del año y los posibles escenarios como horario diurno y nocturno. Intentar obtener modelos segregados implica interrumpir la continuidad del fenómeno y se traduce en una reducción en la correlación del modelo.

La expresión para la velocidad del viento que se propone, no depende directamente de la longitud de rugosidad sino de tres parámetros, que para cualquier otra localidad deberán ser determinados experimentalmente y que capturan el efecto variable de la longitud de rugosidad.

Con la metodología propuesta en esta investigación es posible conocer el valor de la velocidad del viento en el eje vertical, únicamente con realizar mediciones en un punto cercano al suelo, lo que permite conocer el recurso eólico sin necesidad de instalar equipos de gran envergadura.

Agradecimientos

Al Instituto Meteorológico Nacional y al Ing. Maikel Méndez Morales por facilitar los datos para esta investigación. A los estudiantes asistentes Emanuel Fallas y Gonzalo Madrigal por su colaboración con este documento. Al profesor Benito Stradi por el soporte con Cloud Computing. Al ITCR por el financiamiento mediante el proyecto: Optimización de un perfil aerodinámico de una turbina eólica de eje horizontal para aplicaciones de pequeña escala en zonas boscosas.

Referencias

[1] A. Tummala, R. K. Velamati, D. K. Sinha, V. Indraja y V. H. Krishna, “A review on small scale wind turbines,” Renew. Sust. Energ. Rev., vol. 56, pp. 1351-1371, 2016, doi: https://doi.org/10.1016/j.rser.2015.12.027

[2] “Plan Nacional de Energía 2015-2030,” MINAET, San José, Costa Rica, 2015.

[3] FAO, Situación de los bosques del mundo. Los bosques y la agricultura: desafíos y oportunidades en relación con el uso de la tierra. Roma, Italia, 2016.

[4] J. D. Holmes, Wind loading of structures, EUA: CRC Press, 2018.

[5] T. Foken y C. J. Napo, Micrometeorology, vo1. 2, Berlin, Alemania: Springer.

[6] K. Sunderland, T. Woolmington, J. Blackledge y M. Conlon, “Small wind turbines in turbulent (urban) environments: A consideration of normal and Weibull distributions for power prediction,” J. Wind. Eng. Ind., vol. 121, pp. 70-81, 2013, doi: https://doi.org/10.1016/j.jweia.2013.08.001

[7] S. Mertens, “Book Review: Wind Energy in the Built Environment —Concentrator Effects of Buildings,” Wind. Eng., vol. 30, n. 5, pp. 451–452, 2006, doi: http://dx.doi.org/10.1260/030952406779502623

[8] W. Tong, “Fundamentals of wind energy”, en Wind Power Generation and Wind Turbine Design, CIUDAD, PAÍS: WIT Press, 2010, pp 1-44.

[9] M. Beccali, G. Cirrincione, A. Marvuglia y C. Serporta, “Estimation of wind velocity over a complex terrain using the Generalized Mapping Regressor”, Appl. Energy, vol. 87, n. 3, pp. 884-893, 2010, doi: https://doi.org/10.1016/j.apenergy.2009.05.026

[10] L. Kang, J. Zhang, X. Zou, H. Cheng, C. Zhang y Z. Yang, “Experimental investigation of the aerodynamic roughness length for flexible plants,” Bound.-Layer Meteorol., vol. 172, n. 3, pp. 397-416, 2019, doi: https://doi.org/10.1007/s10546-019-00449-0

[11] A. Rigden, D. Li y G. Salvucci, “Dependence of thermal roughness length on friction velocity across land cover types: A synthesis analysis using AmeriFlux data,” Agric. For. Meteorol., vol. 249, pp. 512-519, 2018, doi: https://doi.org/10.1016/j.agrformet.2017.06.003

[12] E. S. Miles, J. F. Steiner y F. Brun, “Highly variable aerodynamic roughness length (z0) for a hummocky debris-covered glacier,” J. Geophys. Res., vol. 122, n. 16, pp. 8447-8466, 2017, doi: https://doi.org/10.1002/2017JD026510

[13] K. D. Maurer, B. S. Hardiman, C. S. Vogel y G. Bohrer, “Canopy-structure effects on surface roughness parameters: Observations in a Great Lakes mixed-deciduous forest,” Agric. For. Meteorol., vol. 177, pp. 24-34, 2013, doi: https://doi.org/10.1016/j.agrformet.2013.04.002

[14] J. T. Millward-Hopkins, A. S. Tomlin, L. Ma, D. B. Ingham y M. Pourkashanian, “Mapping the wind resource over UK cities,” Renew. Energy, vol. 55, pp. 202-211, 2013, doi: https://doi.org/10.1016/j.renene.2012.12.039

[15] S. M. Weekes y A. S. Tomlin, “Evaluation of a semi-empirical model for predicting the wind energy resource relevant to small-scale wind turbines,” Renew. Energy, vol. 50, pp. 280-288, 2013, doi: https://doi.org/10.1016/j.renene.2012.06.053

[16] L. É. Boudrealt, A. Bechmann, N.N. Sørensen, A. Sogachev y E. Dellwik, “Canopy structure effects on the wind at a complex forested sites,” J. Phys. Conf. Ser., vol. 524, no. 1, p. 012112, 2014, doi: https://doi.org/10.1088/1742-6596/524/1/012112

[17] L. É. Boudrealt, A. Bechmann, L. Tarvainen, L. Klemedtsson, I. Shendryk y E. Dellwik, “A LiDAR method of canopy structure retrieval for wind modeling of heterogeneous forests,” Agric. For. Meteorol., vol. 201, pp. 86-97, 2015, doi: https://doi.org/10.1016/j.agrformet.2014.10.014

[18] D. Hu, S. Cao, S. Chen y N. Feng, “Mapping aerodynamic roughness length with multi-source remote sensing data,” en 2016 4th. Int. Workshop on Earth Obs. Remote Sens. App. (EORSA), 2016, pp. 373-376, doi: https://doi.org/10.1109/EORSA.2016.7552832

---