Variabilidade espacial da palha de soja distribuída na colheita e sua relação com o estande final de aveia preta

Spatial variability of soybean straw distributed at harvest and its relationship with the final stand of black oats

Júlio Tagliari-Balestrin1, David Peres-da-Rosa2, Bruno Cazaroto3

Fecha de recepción: 31 de agosto de 2020
Fecha de aprobación: 18 de diciembre de 2020

Tagliari-Balestrin, J; Peres-da-Rosa, D; Cazaroto, B. Variabilidade espacial da palha de soja distribuída na colheita e sua relação com o estande final de aveia preta. Tecnología en Marcha. Vol. 34-4 Octubre-Diciembre 2021. Pág 28-37.

https://doi.org/10.18845/tm.v34i4.5320

Palavras chave

Plantio direto; colhedora; resíduo vegetal; variabilidade espacial.

Resumo

Objetivo desse trabalho foi avaliar o efeito da variabilidade espacial da distribuição da palha na colheita da soja na emergência de aveia preta em sistema plantio direto. O experimento foi conduzido em uma área agrícola de 2,6 ha, sendo avaliados a quantidade de palha (kg ha-1) de soja distribuida pela colhedora, e o estande final de aveia preta (plantas m-2). Foi empregado um gride amostral de 20 pontos, sendo 10 pontos no centro da colhedora e os outros 10 nas extremidades. Nos pontos no centro da colhedora, a quantidade de palha variou de 6.424 a 12.000 kg ha-1 ( = 8.788 ± 1.669 kg ha-1), já o estande final de plantas de aveia preta variou de 165 a 212 plantas m-2 ( = 191 ± 14 plantas m-2). Nos pontos relativos às extremidades, a quantidade de palha reduziu, variando de 1.697 a 3.394 kg ha-1 ( = 2.448 ± 588 kg ha-1), e estande final de plantas de aveia preta aumentou para 267 a 306 plantas m-2 ( = 285 ± 13 plantas m-2), ou seja, redução de 72,14% na quantidade de palha e um aumento de 49,21% no estande. As variáveis analisadas apresentaram correlação forte, negativa e significativa (r = - 0,887; P ˂ 0,05), desde modo, a colhedora empregada no estudo distribui a palha desuniforme, sendo que esta ação afeta o estande final da aveia preta.

Keywords

No-tillage; combine; plant residue; spatial variability.

Abstract

The objective of this work was to evaluate the effect of spatial variability straw distribution on soybean harvest in the emergence of black oats in no-tillage system. The experiment was carried out in an agricultural area of 2.6 ha, being evaluated the amount of soybean straw (kg ha-1) distributed by the harvester, and the final stand of black oats (plants m-2). A 20-point sampling grid was used, 10 points in the center of the harvester and the other 10 at the ends. At the points in the center of the harvester, the amount of straw varied from 6,424 to 12,000 kg ha-1 ( = 8,788 ± 1,669 kg ha-1), while the final stand of black oat plants ranged from 165 to 212 plants m-2 ( = 191 ± 14 plants m-2). In the points related to the ends, the amount of straw reduce to 1,697 to 3,394 kg ha-1 ( = 2,448 ± 588 kg ha-1) and the final stand of black oat increase to 267 to 306 plants m-2 ( = 285 ± 13 plants m-2), that is, a reduction of 72.14% in the amount of straw and an increase of 49.21% in the stand. The variables analyzed showed a strong, negative and significant correlation (r = - 0.887; P ˂ 0.05), therefore, the combine used in this study distributes the uneven straw, and this action affects the final stand of black oats.

Introdução

O Sistema de Plantio Direto (SPD) propõe uso contínuo de cobertura do solo na lavoura, através da deposição de restos vegetais de culturas advindas do processo de rotação cultural [1]. A palha na superfície do solo oferece diversos benefícios, como a dissipação da energia do impacto da gota de chuva, aumento da infiltração de água, manutenção da umidade, melhoria da macro e micro fauna, redução da amplitude térmica, menores perdas por erosão e diminuição da incidência de plantas daninhas [2], bem como, amortecimento da pressão imputada no tráfego.

Anualmente o aporte de palha para o sistema de plantio direto deve ser de 10 a 12 t ha-1 [3], nesse sentido, uma das etapas fundamentais do manejo da palha ocorre no momento da colheita, uma vez que as máquinas empregadas na operação são responsáveis por fazer a distribuição dos restos culturais ao solo. É de fundamental importância que esses restos culturais sejam distribuídos de forma homogênea ao solo, buscando evitar locais de acúmulo de palha, haja visto que ocasionarão problemas de embuchamento na semeadora no momento da semeadura da próxima cultura, além de irregularidades na profundidade das sementes. Já na condição contrária, ausência de palha, o problema está na maior propensão ao desenvolvimento de plantas daninhas [4]. Diferentes concentrações de palha também podem refletir no aparecimento de faixas de fertilidade diferentes, bem como, podem gerar redução do contato solo/semente, resultando em faixas com menor emergência de plântulas [5]. Ademais, a maior concentração de palha gerada pela irregularidade de distribuição dos restos culturais realizada pela colhedora, pode resultar em menores percentuais de emergência da cultura subsequente [6].

A cultura de aveia preta (Avena strigosa) é muito utilizada no Sul do Brasil durante o inverno, para fins de cobertura de solo, por produzir alta quantidade de palha, ao redor de 4 t ha-1 [7]. Sua utilização traz inúmeros benefícios para as culturas de verão, quando comparado a prática de pousio durante o período de inverno. Entretanto, a efetividade desta alternativa de cobertura de solo se dá, em grande parte, em virtude do estande de plantas e esse, por sua vez, está aliado a emergência uniforme das plântulas.

Neste sentido, o presente estudo objetivou avaliar o efeito espacial da irregularidade de distribuição de restos culturais da colheita de soja no estande final de aveia preta.

Material e métodos

O experimento foi conduzido via técnicas de agricultura de precisão, geoestatística, realizado em uma área agrícola de 2,6 hectares localizada no município de Sertão/RS no ano agrícola 2018/2019. Situado a 28°0’34”S e 52°25’4”O e altitude de 620 metros, o local possui clima subtropical úmido (cfa), com chuvas bem distribuídas e temperatura média anual de 18,3°C [8], o solo é classificado como Nitossolo Vermelho Distrófico [9]. A área é manejada em SPD há mais de 30 anos, na qual são cultivadas grandes culturas, como soja, trigo e aveia preta.

Para implantação do experimento, um gride de 20 pontos foi determinado na área, sendo 10 pontos relativos ao centro da colhedora e os outros 10 à extremidade (figura 1). Os parâmetros avaliados foram a quantidade de palha e o estande final de plantas emergidas de aveia preta. Para o primeiro parâmetro, foi extraída a massa de palha presente em 1 m2, esta foi pesada e estimada seu valor por hectare, parâmetro mensurado no dia que foi realizada a semeadura de aveia preta. Após a emergência total da aveia preta, foi determinada o estande de plantas por m2 nos mesmos pontos amostrais anteriores.

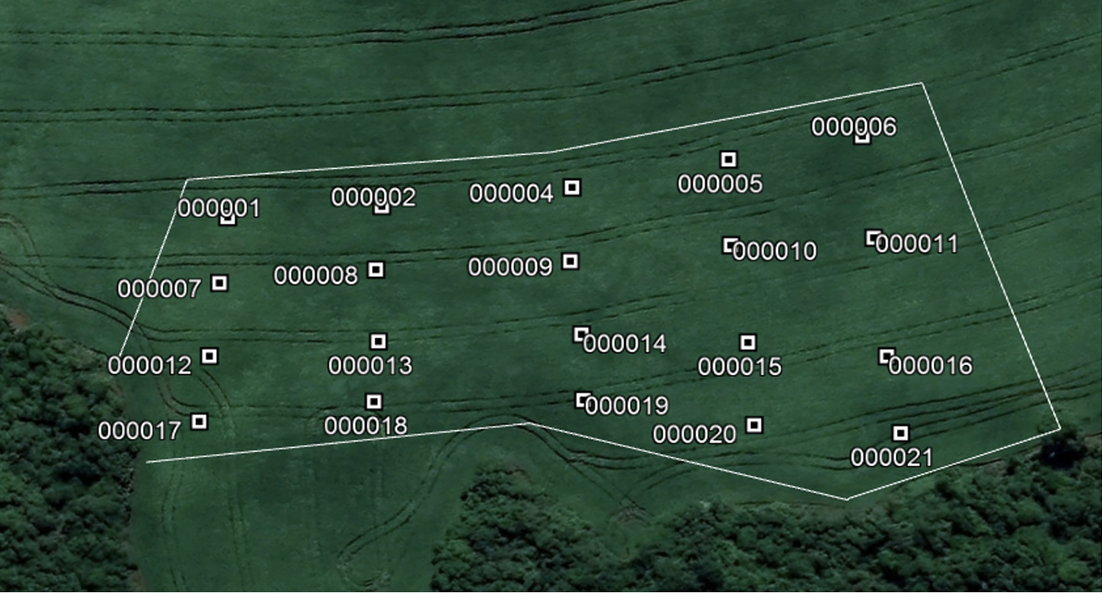
Figura 1. Gride da área experimental no município de Sertão, RS, Brasil. Pontos 1-6 e 12-16: centro da colhedora. Pontos 7-11 e 17-21: extremidade da colhedora. Fonte: Google Earth.

A colheita da soja foi realizada com uma colhedora New Holland® 2017 modelo TC 5070 equipada com plataforma de 20 pés. Para delimitação da área, e georreferenciamento dos pontos, foi empregado um GNSS portátil Garmin® Etrex 20, sendo os dados tabelados em planilha eletrônica.

Os mapas de isolinhas foram construídos por meio de interpolação por krigagem ordinária, levando-se em conta os parâmetros do semivariograma determinados pela análise geoestatística, utilizando o software CR Campeiro 7®.

Afim de verificar diferenças estatísticas dos parâmetros, os dados foram submetidos à análise de variância (ANOVA), teste de normalidade e comparação de médias pelo teste de Tukey à 5% de significância, utilizando o software SISVAR®. A estatística exploratória dos dados (estatística descritiva) foi realizada com auxílio do software PAST®, sendo obtidas medidas de posição (mínimo, média e máximo) e de dispersão (desvio padrão, coeficientes de variação (CV%), assimetria e de curtose). Com base nos valores de assimetria (Cs) obtidos, visando caracterizar quanto e como a distribuição de frequências se afasta da simetria, foram classificados como: Cs = 0 distribuição simétrica, Cs > 0 distribuição assimétrica à direita e Cs < 0 distribuição assimétrica à esquerda. Os valores de curtose (Ck), que expressam a dispersão (achatamento) da distribuição em relação a um padrão, geralmente utilizada a curva normal, foram classificados em: Ck = 0 distribuição mesocúrtica, Ck < 0 distribuição platicúrtica e Ck > 0 distribuição leptocúrtica.

Com base nos valores de CV(%) dos dados, a dispersão dos dados foi classificada em: baixa para CV <15%; moderada, para CV de 15 a 35%; e alta, para CV>35% [10].

Foi realizado teste de correlação linear de Pearson (r) para avaliar o grau de correlação entre as variáveis analisadas. Este coeficiente expressa numericamente, tanto a força quanto o sentido da correlação. Seu valor varia entre 1 e -1 ou seja: -1 ≤ R ≤ 1. Se R = 1, as duas variáveis relacionadas têm correlação perfeitamente positivas; se R = -1, as duas variáveis relacionadas têm correlação perfeitamente negativa; se R = 0, não existe correlação entre as duas variáveis correlacionadas. Quanto mais próximo de 1 (+ ou -), maior a força de correlação [11].

A análise geoestatística foi realizada por meio do ajuste de semivariogramas experimentais, através do software CR Campeiro 7®, determinando efeito pepita (C0), contribuição (C1), patamar (C0+C1), alcance (a) e índice de dependencia espacial (IDE). O IDE foi calculado por meio das equações: IDE=x[C1/(C0+C1)]*[a/(0,5MD)]*100, em que x são constantes (0,375, 0,317 e 0,504 para os modelos esférico, exponencial e gaussiano, respectivamente) e MD é a máxima distancia entre pontos. Se a razão a/0,5MD for maior que 1, utiliza-se 1. Com base no IDE, classificou-se a dependência espacial para o modelo esférico: ≤ 7% (fraco), entre 7% e 15% (moderado) e > 15% (forte); para o modelo exponencial: ≤ 6% (fraco), entre 6% e 13% (moderado) e > 13% (forte); e para o modelo gaussiano: ≤ 9% (fraco), entre 9% e 20% (moderado) e > 20% (forte) [12].

Resultados e discussão

A quantidade de palha de soja foi maior na área correspondente ao centro da colhedora, diferindo significativamente em relação a extremidade (tabela 1). No estande final de plantas de aveia preta ocorreu o contrário, foi maior na área das extremidades, diferindo significativamente em relação ao centro, isto demonstra uma relação, em que conforme aumenta a quantidade de palha ocorre a redução do estande final de aveia preta.

Tabela 1. Quantidade de palha de soja (kg ha-1) e estande final de plantas de aveia preta (plantas m-2) em função da posição da colhedora.

	Posição da colhedora	Amplitude	Média
Palha de soja (kg ha-1)	Centro	6424,24-12000,00	8787,88 a*
	Extremidade	1696,97-3393,94	2448,48 b
Estande final de aveia preta (plantas m-2)	Centro	164,71-211,76	190,59 b
	Extremidade	266,67-305,88	285,49 a

*Médias seguidas de letras distintas minúsculas nas colunas diferem entre si pelo teste de Tukey a 5% de probabilidade.

A quantidade de palha distribuída pela colhedora foi espalhada irregularmente, de maneira que se concentra na centro e na medida que se direciona para as extremidades vai reduzindo. Isso demostra uma desuniformidade na distribuição da palha dentro da largura da plataforma de corte, fato também é relatado por [3] [13] [14].

A quantidade média de palha de soja na área
(tabela 2) foi de 5618,18 kg ha-1, variando de 1696,97 a 12000,00 kg ha-1, já estande médio foi de 238,04 plantas m-2, variando de 164,71 a 305,88 plantas m-2, essa variação é elevada, fato que confirma que há variação da distribuição pela máquina (tabela 1), sendo visualizado no coeficiente de variação deste, que está classificado como alta dispersão dos dados (heterocedasticidade), já no estande final de plantas de aveia preta há moderada dispersão [10].

Ambos os conjunto de dados não apresentaram distribuição normal (tabela 2), condição evidenciada nos coeficientes de assimetria e de curtose, sendo que valores distantes de zero podem ser indicativos da não normalidade [16]. A variável quantidade de palha demonstrou coeficiente de assimetria deslocado à direita (Cs>0) enquanto a variável estande final de plantas de aveia preta deslocado a esquerda (Cs<0) [10]. O coeficiente de curtose para ambas as variáveis demostrou distribuição platicúrtica (Ck<0) [10], o que demostra que as curvas de distribuição dos dados da quantidade de palha e do estande final de plantas de aveia preta são mais achatadas do que a distribuição normal, apresentando variação destes atributos ao longo da área.

Tabela 2. Estatística descritiva da quantidade de palha de soja (kg ha-1) e do estande final de aveia preta (plantas m2).

Parâmetros	Quantidade de palha de soja	Estande final de aveia preta
Mínimo	1696,97	164,71
Média	5618,18	238,04
Máximo	12000,00	305,88
Desvio padrão	3472,61	50,46
Coef. De variação (%)	61,81	21,20
Cs	0,33	-0,02
Ck	-1,47	-1,88
W	0,87*	0,85*

Cs = Coeficiente de assimetria; Ck = Coeficiente de curtose. W = Teste de Shapiro-Wilk para distribuição normal, onde (*) significativo em níveis de p <0,05. Quando for significativo indica que a hipótese para distribuição normal é rejeitada.

O efeito pepita demonstra a variabilidade não explicada pelo modelo geoestatístico, levando em consideração a distância de amostragem utilizada, assim a análise do efeito pepita é de grande importância, pois, quanto menor for o seu valor, maior será a continuidade do fenômeno e menor será a variância da estimativa [17]. Os valores encontrados nesse estudo (tabela 3) indicam que o erro foi bastante elevado no estande de plantas, demonstrando a alta variabilidade dos dados dentro da variável.

Tabela 3. Análise geoestatística da quantidade de palha de soja e do estande final de plantas de aveia preta.

Parâmetros Geoestatísticos	Quantidade de palha de soja	Estande final de plantas de aveia preta
C0	6,66	2272,55
(C0 + C1)	12,06	2551,16
C1	5,4	278,61
a	100	100
Modelo	Gaussiano	Esférico
r2	0,76	0,98
IDE	22,57	4,10
Classe	Forte	Fraco

C0 = Efeito pepita; (C0 + C1) = Patamar; C1 = Contribuição; A = Alcance (m); IDE = Índice de dependência espacial.

Quanto menor for a proporção do efeito pepita para o patamar do variograma, maior será a continuidade do fenômeno e a variância da estimativa, e maior será a confiança que se pode ter na estimativa [18], sendo calculada pelo índice de dependencia espacial. A quantidade de palha apresentou dependência espacial classificada como forte, ou seja, tem variação na área, confirmando a discussão demonstrada anteriormente (tabela 1) na comparação entre as posições de coleta. Esse fato comprova que são necessárias alterações construtivas nas colhedoras agrícolas, haja visto que atualmente o que mais é focado é no aumento da capacidade de campo operacional. Avaliando a distribuição da palha de soja em diferentes colhedoras, [13] constataram que a distribuição transversal da palha foi desuniforme, independente do mecanismo de trilha e da largura da plataforma, sendo verificado acúmulo de palha no centro da linha de deslocamento e pouco nas extremidades. Na colheita de trigo, a distribuição também foi irregular, conforme relatado nos estudos de [20] [21], sendo constatado também, maior acúmulo de palha no centro das máquinas. Isto demonstra que a irregularidade de distribuição de palha das colhedoras é um problema recorrente na agricultura.

No estande final da aveia preta, o IDE foi classificado como dependência fraca, fato que pode estar relacionado à rusticidade desta planta, pois consegue emergir mesmo em condições não tão favoráveis ao desenvolvimento pleno, haja vista, que é possível ver uma relação deste parâmetro com a quantidade de palha (tabela ١), de forma inversa, conforme um aumenta, o outro reduz.

Para a quantidade de palha o modelo teórico que possibilitou os melhores ajustes dos semivariogramas foi o gaussiano, já para o estande final de aveia preta foi o esférico. O modelo gaussiano apresenta um comportamento parabólico próximo da origem e representa fenômenos extremamente contínuos. Já o modelo esférico tem um comportamento linear próximo da origem que representa fenômenos contínuos, mas não diferenciáveis [15]. Tais modelos expressam bem a variação dos dados, em que no primeiro parâmetro observou-se IDE forte, bem como, a sua variação nos dados de CV.

O alcance é um critério importante para estudos de geoestatística, significa a distância máxima que a variável em estudo está correlacionada espacialmente, ou seja, maiores valores de alcance contribuem para uma maior confiança nas estimativas feitas [19]. Para os valores de alcance não houve diferença entre as variáveis analisadas, desta forma, a equidistância da grade amostral foi suficiente para descrever as propriedades avaliadas com exatidão, pois os valores de alcance encontrados para as diferentes propriedades são superiores a da grade.

As variáveis analisadas apresentaram correlação forte, negativa e significativa (r = -0,887; p ˂ 0,05) [11], logo, assim como já foi sinalizado nos dados anteriores, quanto maior a quantidade de palha de soja, menor é o estande de aveia preta (figura 2).

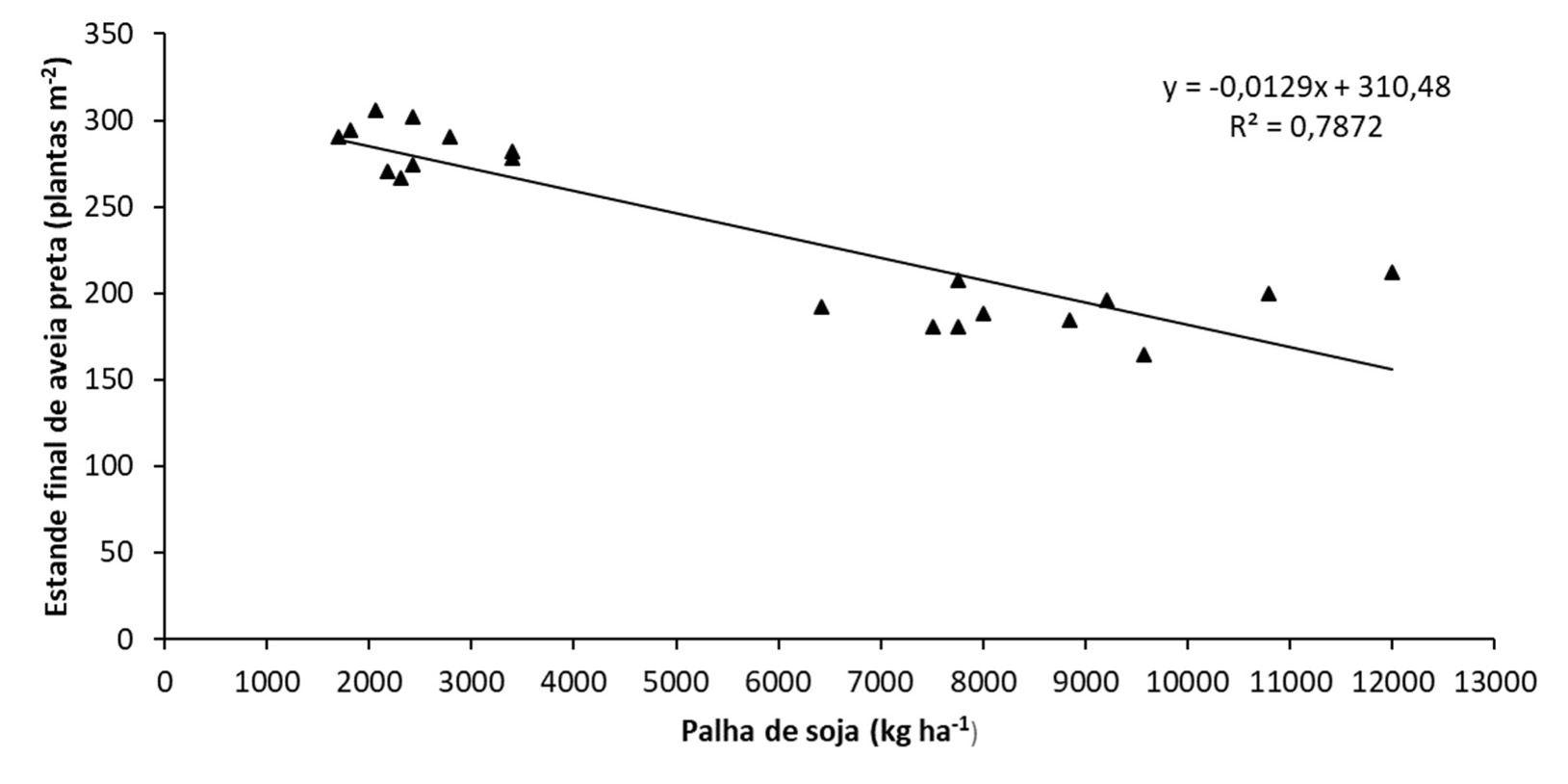
Figura 2. Correlação entre o estande final da aveia preta com a quantidade de palha de soja.

Os mapas de isolinhas da quantidade de palha de soja (figura 3A) e estande final de plantas de aveia preta (figura 3B) demonstram a existência de variabilidade espacial ao longo da área. Os locais em que há maior presença de palha coincidem com aqueles em que há menor estande final de plantas de aveia preta, corroborando para a existência de correlação negativa entre as variáveis (figura 2).

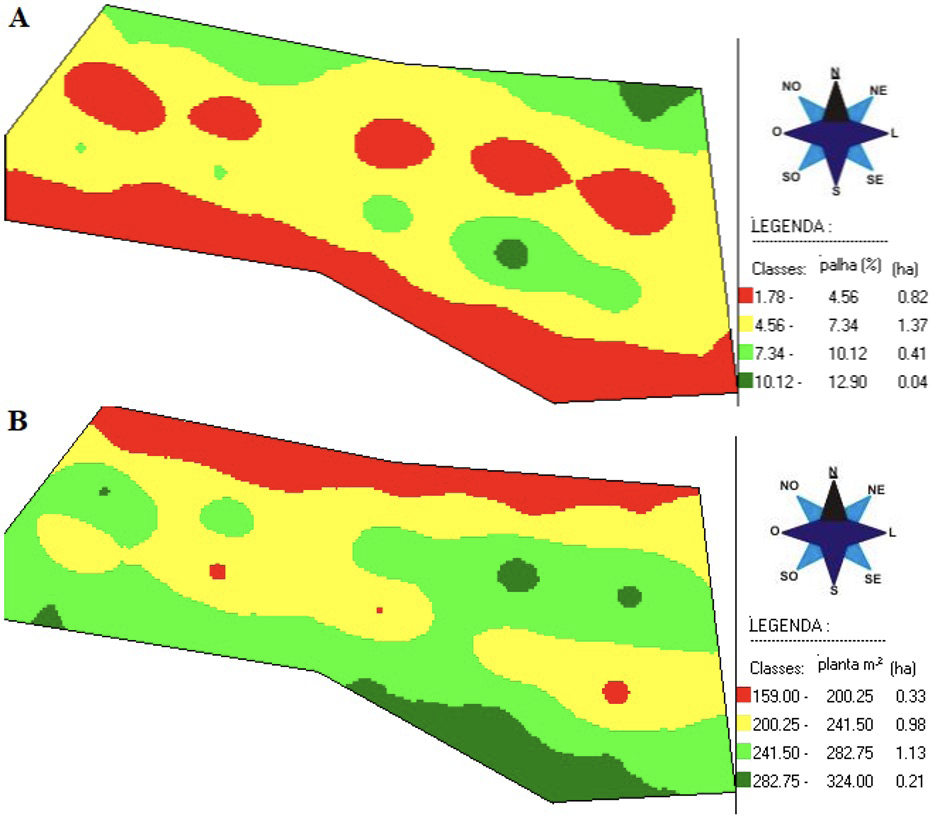
Figura 3. Mapas interpolados por “krigragem” da variabilidade espacial da quantidade de palha de soja (kg ha-1) (A) e do estande final de plantas de aveia preta (plantas m-2) (B).

A distribuição de palha ficou 51,70% da área concentrada entre 4560 a 7340 kg ha-1, zona mais central da área, local em que a emergência foi 36,98% concentrada no estande final de plantas médio, variando de 200,50 a 241,50 plantas m-2. O maior estande final de aveia preta, classe de 282,75 a 324,00 plantas m-2, ocorreu em apenas 7,92% da área, zona essa que teve a menor classe de quantidade de palha, 1780 a 4650 kg ha-1, demonstrando ação da correlação negativa (Figura 2). A maior parte do resíduo acumulado no centro da linha de deslocamento da colhedora corresponde ao palhiço (material oriundo das peneiras) [21], desta forma, [20] destacam a importância de um sistema de distribuição de palhiço, visando a obtenção de uma distribuição de palha mais homogênea, visto que, atualmente, a maioria das colhedoras possuem apenas aletas difusoras para distribuir palha no picador, sem a presença de um mecanismo distribuidor de palha nas peneiras. Na colhedora avaliada, embora possuindo no bandejão divisões para distribuir melhor o volume de palha sobre o sistema de peneira, a oscilação do terreno acaba direcionando a palha de maneira desuniforme, resultando nesse problema.

Nos locais com acúmulo de palha, forma-se uma barreira física que pode atrasar e/ou impedir o surgimento de plântulas, comprometendo o estande de plantas. Conforme [22], a condição heterotrófica das plântulas (sobrevivência às custas das reservas da semente) permite a elas sobrevir por um curto período de tempo na ausência de luz, no entanto, a com o passar do tempo, a medida em que se tornam autotróficas, é necessário haver a presença de luz para a manutenção das atividades fisiológicas. Portanto, a aveia preta germina, mas não consegue se desenvolver, devido a barreira física gerada pelo excesso de palha de soja que impede a entrada de luz até as plantas, levando-as à morte. Resultados similares foram encontrados por [6], que ao estudarem o efeito da palha de soja na emergência de trigo concluíram que o aumento da palha na superfície do solo reduz a emergência das plântulas. A emergência de soja e milho também são afetadas pelo excesso de palha, fato relacionado a maior dificuldade de corte dos mecanismos das semeadoras [23].

A quantidade de palha não é importante só na emergência da aveia preta, a palha possui efeito no manejo de fertilidade do solo, uma vez que a decomposição libera nutrientes ao meio [2]. Este processo, dentro de um sistema de agricultura de precisão, que preconiza pela homogeneidade dos atributos químicos do solo, é fundamental.

A desuniformidade de palha na área (figura 3A) irá repercutir em problemas com plantas daninhas, conforme relatam [24], que a palha assume grande importância no manejo destas, uma vez que ela tem a capacidade de influenciar na dormência, germinação e mortalidade de determinadas espécies daninhas, provocando modificações nas comunidades infestantes. Desta forma, nos locais em que há menor presença de palha de soja, possivelmente haverá maior incidência de plantas daninhas competindo com a cultura da aveia preta.

Embora a manutenção da palha das culturas sobre a superfície do solo seja uma importante prática conservacionista de solo, quando mal manejada pode afetar a emergência das sementes de plantas cultivadas. Neste sentido, a palha precisa garantir a máxima proteção do solo e ao mesmo tempo causar o menor efeito possível sobre a emergência das culturas. A maneira mais prática de gerenciar os resíduos da colheita é com a colhedora. A palha, portanto, deve ser espalhada uniformemente por toda a largura da plataforma de corte.

Conclusões

A variabilidade da distribuição da palha na colheita da soja influencia no estande final da aveia preta, havendo forte correlação entre estes parâmetros e variabilidade espacial de ambos.

Referencias

[1] I. Bertol, O. Ciprandi, C. Kurtz and A. S Baptista, “Persistência dos resíduos culturais de aveia e milho sobre a superfície do solo em semeadura direta”, Revista Brasileira de Ciência do Solo, vol. 22, pp. 705-712, 1998.

[2] C. A Chioderoli, R. P. Silva, R. H. F Noronha, M. T Cassia and E. P Santos, “Perdas de grãos e distribuição de palha na colheita mecanizada de soja”, Bragantia, vol. 71, pp. 112-121, 2012.

[3] C. BAYER, L. Martin-Neto, J. Mielniczuk, A. Pavinato and J. Dieckow, “Carbon sequestration in two Brazilian Cerrado soils under no-till”, Soil & Tillage Research, vol. 86, pp. 237-245, 2006.

[4] N. V. Costa, A. C. P. Rodrigues-Costa, E. M. P Coelho, S. D. Ferreira, J. A. Barbosa, “Métodos de controle de plantas daninhas em sistemas orgânicos: breve revisão”, Revista Brasileira de Herbicidas, vol. 17, pp. 25-44, 2018.

[5] N. M. Correia and J. C. Durigan, “Culturas de cobertura e sua influência na fertilidade do solo sob sistema de plantio direto (SPD)”, Bioscience Journal, vol. 24, pp. 20-31, 2008.

[6] J. Abati, C. R. Brzezinski, C. Zucareli, F. Werner and F. A Henning, “Seed vigor and amount of soybean straw on seedling emergence and productive performance of wheat”, Semina: Ciências Agrárias, vol. 38, pp. 2179-2186, 2017.

[7] S. O. Chini, “Variabilidade em germoplasma de aveia-preta quanto a caracteres relacionados à aptidão forrageira ou cobertura do solo”, Tese (Doutorado), Universidade de Passo Fundo, Passo Fundo/RS, 2017.

[8] A. M. Ramos, L. A. R. Santos and L. T. G Fortes, “Normais Climatológicas do Brasil 1961–1990” INMET, Brasília/DF, 2009.

[9] H. G. dos Santos, P. K. T. Jacomine, L. H. C. dos Anjos, V. A. de Oliveira, J. F. Lumbreras, M. R. Coelho, J. A. de Almeida, T. J. F. Cunha and J. B. de Oliveira, “Sistema brasileiro de classificação de solos”, 3. ed. rev. ampl. Brasilia: EMBRAPA, 353 p., 2013.

[10] F. Pimentel-Gomes and C. H. Garcia, “Estatística aplicada a experimentos agronômicos e florestais”, Piracicaba FEALQ : 309, 2002.

[11] D. B. Figueiredo Filho and J. A. Silva Júnior, “Desvendando os mistérios do coeficiente de correlação de Pearson (r)”, Revista Política Hoje, vol. 18, pp. 115-46, 2009.

[12] E. J. Seidel and M. S. Oliveira, “A classification for a geostatistical index of spatial dependence”, Revista Brasileira de Ciência do Solo, vol. 40, pp. 1-10, 2016.

[13] V. L. Kunz, A. G Filho, M. A Primo, F. Gurgacz and E. Fey, “Distribuição de palha por colhedoras autopropelidas na colheita da soja”, Engenharia Agrícola, vol. 28, pp. 125-135, 2008.

[14] L. O. B. Schuch, J. L. Nedel, M. S. Maia, F. N. Assis, F. N. de, “Vigor de sementes e análise de crescimento de aveia-preta”, Scientia Agricola, vol. 57, pp. 305-312, 2000.

[15] E. C. G. Camargo, “Geoestatística: Fundamentos e aplicações” In: G, Câmara and J. S. Medeiros (eds) Geoprocessamento para projetos ambientais. INPE, São José dos Campos: INPE, 1998.

[16] G. Milone, “Estatística Geral e Aplicada”, Pioneira Thomson Learning, São Paulo/SP, 2004.

[17] E. H. Isaaks and R. M. Srivastava, “An introduction to applied geostatistics”, Oxford University, New York, 561 p., 1989.

[18] E. C. Guimarães, “Geoestatística básica e aplicada”, Universidade Federal de Uberlândia, Uberlândia/MG, 77 p., 2004.

[19] J. E. Corá, A. V. Araújo, G. T. Pereira and J. M. G. Beraldo, “Variabilidade espacial de atributos do solo para adoção do sistema de agricultura de precisão na cultura de cana-de-açúcar” Revista Brasileira de Ciência do solo, vol. 28, pp. 1013-1021, 2004.

[20] A. F. Orlando, E. Fey, T. Pedron, E. Lima and L. Primo, “Uniformidade de distribuição dos resíduos da cultura do trigo em colhedoras autopropelidas”, In: Jornada Científica da Unioeste, Marechal Cândido Rondon/PR, 2005.

[21] R. J. Veseth, C. F. Engle, J. A. Vomocil and R. E. Mcdole, “Uniform combine residue distribution for successful no-till and minimum tillage systems”, Pacific Northwest Extension Publication, vol. 7, pp. 1-7, 1986.

[22] L. Taiz, E. Zeiger, I. M. Moller and A. Murphy, “Fisiologia e desenvolvimento vegetal”, 6. ed. Porto Alegre: Artmed, 888 p., 2017.

[23] E. C. Mantovani and A. May, “Mecanização” In: I. A. Pereira Filho and J. A. S. Rodrigues (eds) Sorgo: o produtor pergunta, a Embrapa responde. Embrapa, Brasília, pp 41-50, 2015.

[24] M. S. Fileti, E. B. Pinotti, P. D. Epiphanio, B. M. C. Barros, T. F. Silva, M. Girotto, D. P. Silva, C. G. Bosquê and F. C. C. Lima “Utilização de palhada no controle de planta daninha” Revista científica eletrônica de agronomia, ano X, n. 20.

---