Optimización económica para el cultivo de papa, zanahoria y cebolla en Cartago, Costa Rica1
Economic optimization for the cultivation of potatoes, carrots and onions in Cartago, Costa Rica
David Barboza-Navarro2, Johanna Solórzano-Thompson3,
Javier Paniagua-Molina4
Fecha de recepción: 27 de agosto de 2020
Fecha de aprobación: 9 de diciembre de 2020
Barboza-Navarro, D; Solórzano-Thompson, J; Paniagua-Molina, J. Optimización económica para el cultivo de papa, zanahoria y cebolla en Cartago, Costa Rica. Tecnología en Marcha. Vol. 34-4 Octubre-Diciembre 2021. Pág 38-49. https://doi.org/10.18845/tm.v34i4.5184
https://doi.org/10.18845/tm.v34i4.5184
Palabras clave
Programación lineal; restricción económica; función de rentabilidad; rotación de cultivos.
Resumen
La producción de papa, cebolla y zanahoria es de gran importancia económica en la zona norte de la provincia de Cartago. Por esta razón es necesario procurar la optimización de las tierras agrícolas que permita programar la oferta y cumplir con las necesidades y condiciones del mercado nacional. En este estudio se optimizó la rentabilidad anual de sembrar 2,34 hectáreas de papa, cebolla y zanahoria, mediante un modelo de programación lineal. Este trabajo se llevó a cabo durante el primer semestre de 2019 con productores de la zona y se utilizaron datos de fuentes primarias de instituciones relacionadas con el sector agrícola. Se aplicaron dos escenarios de optimización de la función de rentabilidad a partir de restricciones de área aprovechable, capacidad de mercado y presupuesto. En ambos escenarios fue posible optimizar la función de rentabilidad con toda la tierra aprovechable, se respetó el rezago de los ciclos de cultivo y se utilizó el menor presupuesto disponible. La optimización de la rentabilidad de cada cultivo permitió entender el comportamiento de siembra de los productores para obtener la mayor utilización de los recursos, la mejor distribución de siembra y la mayor rentabilidad posible.
Keywords
Linear programming; economic restriction; profitability function; crop rotation.
Abstract
Potato, onion and carrot production is of great economic importance in the northern zone of Cartago province. For this reason, it is necessary to seek the optimization of agricultural land that allows programming the offer and meet the needs and national market conditions. In this study, the annual profitability of sowing 2,34 hectares of potatoes, onions and carrots, using a linear programming model. This work was carried out during the first semester of 2019 with producers in the zone and data from primary sources of institutions related to the agricultural sector were used. Two optimization scenarios of the profitability function were applied based on restrictions of usable area, market capacity and budget. In both scenarios, it was possible to optimize the profitability function with all the usable land, the lag of the crop cycles was respected and the least available budget was used. The profitability optimization of each crop provides an important contribution that allows to understand the sowing behavior of the producers in the search to obtain the greatest use of resources, the best sowing distribution and the highest possible profitability.
Introducción
En el año 2015 en la provincia de Cartago los cultivos anuales ocupaban una extensión aproximada de 10048 ha, de las cuales, el 29,28% eran dedicadas a la producción de papa (Solanum tuberosum L.), el 13,71% a cebolla (Allium cepa L.) y el 6,34% a zanahoria (Daucus carota L.) [1]. Del total de hectáreas (ha) sembradas a nivel nacional de estos tres cultivos, la zona alta de Cartago5 representó para el año 2015 el 78,52%, 84,29% y 73,87%, respectivamente [1].
La planificación de la producción en fincas depende de factores tales como el tipo y calidad del suelo, la tasa de rendimiento, las condiciones climáticas, la disponibilidad de agua e insumos agrícolas, el acceso al capital necesario, los costos de producción, la tecnología aplicada, entre otros. De acuerdo con Osaki y Batalh [2], la propiedad representativa o típica de una estructura de producción agrícola debe incluir las características de un grupo de productores en una región, dado que usan las mismas tecnologías.
En el ámbito de la investigación de operaciones, Render et al. [3] destacan la programación lineal (PL) como una técnica basada en el modelado matemático de una situación para facilitar la toma de decisiones con respecto a la asignación de los recursos, que bien, podrían ser limitados. Para la formulación de estos modelos existen tres elementos indispensables de identificar: a) las variables de decisión, b) la función objetivo y c) las restricciones [4]. Los modelos de PL han tenido un papel importante en investigaciones agrícolas, en especial cuando se trabaja con sistemas productivos en rotación de cultivos [5].
La programación lineal en el campo de la agricultura es una herramienta de gran utilidad debido a su capacidad para resolver problemas del mundo real, al cumplir con objetivos como la maximización de utilidades o la minimización de costos [6]. Tal es el caso de Lora-Freyre y Pellicer-Durán [7] que utilizaron PL para maximizar la producción de café y demostrar el aumento en la producción después de mejorar el plan de distribución de tierras. Bedoya-Cardoso y Salazar-Moreno [8] se enfocaron en la optimización del uso de fertilizantes en el cultivo de café y demostraron una minimización en los costos de fertilización; mientras que Miller et al. [9] minimizaron el costo total del empacado de tomate.
Para mejorar el balance alimentario en una lechería tropical se utilizó un modelo PL que permitió la distribución óptima del área utilizada para la producción de forrajes [10]. También se optimizó el uso del recurso hídrico para estimar la superficie de riego y el patrón de cultivos ideal para incrementar los beneficios netos de los productores afectados por los efectos negativos de la sequía en la agricultura, por lo que propició una reducción en la superficie de riego [11].
En lo que respecta a la maximización de beneficios, Mohamad y Said [12] desarrollaron un modelo de PL con cultivos de cosecha única, al tomar en cuenta el problema que sufren algunos agricultores en Malasia al definir qué, cuánto y cuándo sembrar. El beneficio total se maximizó en el escenario que disponía el mayor capital posible y los menores gastos administrativos, para implementar la combinación de los cultivos pak choi y lechuga.
En la región de Trigay, Etiopia, se efectuó un análisis de sensibilidad para un modelo de PL que optimizara el patrón de cultivo en función de maximizar el beneficio [13]. El modelo concluyó acerca del nivel de sensibilidad en la agricultura con respecto a la producción de cultivos como verduras, cereales, legumbres y frutas y verduras, combinadas o no con cereales [13].
Con el uso de modelación avanzada que incorpore el riesgo mediante una variante del método MOTAD6, se diseñó un modelo PL para una granja en Oregon [5]. Del mismo modo, su finalidad fue la maximización de beneficios, a través de todas las combinaciones posibles en un sistema de rotación y la inexistencia de limitantes en los recursos productivos. El objetivo se cumplió con una rotación continua de trigo, patatas, trigo, patatas y maíz, respectivamente. El análisis de caso fue dominado por el cultivo con el mayor retorno por acre, mismo que se ve reducido al incorporar otros cultivos para evitar la pérdida de propiedades del suelo [5].
En Brasil también se incoporó el riesgo en un modelo de PL para la producción de soja temprana, soja normal y maíz, con restricciones de capital inicial, al menos dos cosechas anuales, disponibilidad de horas máquina y de parcelas en el tiempo, y una rotación continua de soja temprana seguida por maíz [2]. El modelo maximizó el margen de contribución bruta sujeto al riesgo, en un área disponible de 1300 ha. La maximización de la contribución generó un beneficio máximo que asume el mayor nivel de riesgo posible. La menor exposición al riesgo se dio al optar por un margen bruto máximo que destinaba 128 ha para soja temprana y maíz, y 1172 ha a la soja normal; con un nivel de riesgo mínimo [2].
En Costa Rica la disponibilidad de investigaciones publicadas acerca de la aplicación de PL en agricultura es limitada. Una investigación de Alvarado-Boirivant [15] determinó que los cultivos de zanahoria, repollo y cebolla bajo un patrón de siembra definido cumplían con el objetivo del modelo, siendo la premisa principal, generar una influencia sobre las PYMES para que realicen este tipo de análisis y asignen sus recursos de manera óptima.
El mismo autor realizó un análisis post-optimal de PL aplicado a la agricultura para maximizar las ganancias e identificar las holguras en los recursos utilizados; esto quiere decir que la totalidad de los recursos disponibles en una situación específica no se utilizan por completo [16]. Posteriormente, se demostró la optimización de siembra en un asentamiento agrícola para 11 cultivos distintos y un área mínima de siembra para cada uno; como resultado se obtuvo una mayor participación en la maximización de los beneficios de los cultivos de chile, papa y vainica [17].
El objetivo de este estudio fue optimizar la rentabilidad económica de sembrar 2,34 ha de papa, cebolla y zanahoria en la zona norte de Cartago, mediante un modelo de programación lineal, para contribuir y fortalecer con la generación de conocimiento en el área de la investigación agrícola costarricense.
Metodología
La programación lineal utiliza un modelo matemático a partir de la determinación de un problema que se desea resolver. Para esto es necesario identificar cual es la función objetivo que se desea optimizar, y cuáles son las restricciones o limitantes relacionadas con la disponibilidad real de recursos [18]. El modelo matemático en su forma estándar es el siguiente:
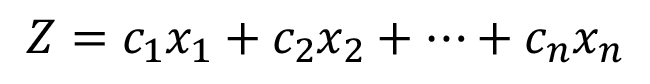 (1a)
(1a)
Sujeta a las restricciones,
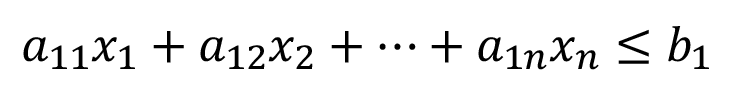 (1b)
(1b)
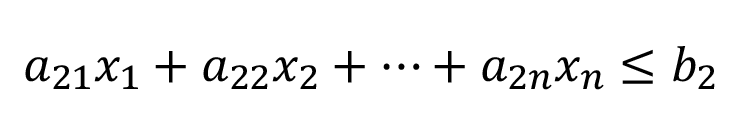 (1c)
(1c)
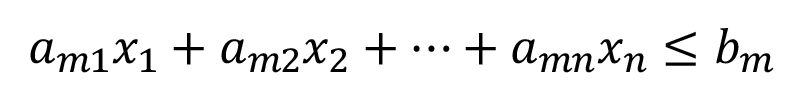 (1d)
(1d)
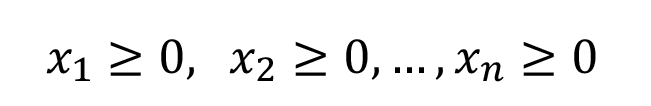 (1e)
(1e)
Los modelos de PL se resuelven a través de una solución interactiva por medio de un algoritmo como es el caso del método Simplex. Este método parte de un planteamiento algebraico utilizando renglones en forma pivotante para convertir las restricciones funcionales de desigualdad en restricciones de igual equivalentes, y reducir la matriz implícita hasta encontrar el óptimo para la función objetivo y las holguras de las restricciones [19] [18].
Datos
En este estudio se utilizaron datos de fuentes secundarias y primarias tanto para la determinación de los ingresos como de los costos, expresados en dólares estadounidenses (USD) al 31 de marzo del 2019. Se utilizó el costo de producción para una hectárea cosechada de cada cultivo a partir de las estructuras de costos publicadas por InfoAgro [20]–[22] y que fueron actualizadas -por este equipo de investigación- a marzo 2019, con cotizaciones de las casas comerciales, y la validación de las labores e insumos utilizados, con productores en la zona de estudio. De la misma manera, los rendimientos por hectárea fueron publicados por InfoAgro [20]–[22] y validados nuevamente con productores.
De acuerdo con las entrevistas a los productores se establecieron los precios promedio en finca por kilogramo (kg) de producto vendido, tanto para papa, cebolla y zanahoria. Además, se analizaron los precios de PIMA7 como referente de comercialización y se utilizó el índice estacional de precios mensual8 del año 2018 (Cuadro 1) a partir de un análisis histórico del periodo 2010-2017 [23] [24]. Aplicar el índice de variación de precios del mercado mayorista permitió estimar el precio posible en los diferentes meses del año.
Cuadro 1. Índice estacional de precios mensuales de papa (Solanum tuberosum L.), cebolla (Allium cepa L.) y zanahoria (Daucus carota L.). Cartago, Costa Rica. 2019.
|
Mes |
Papa |
Cebolla |
Zanahoria |
|
Ene |
5,00% |
34,14% |
-2,78% |
|
Feb |
7,79% |
10,90% |
-15,41% |
|
Mar |
5,19% |
-10,76% |
-7,07% |
|
Abr |
5,45% |
-16,63% |
-4,91% |
|
May |
3,23% |
-12,08% |
-11,44% |
|
Jun |
5,33% |
7,12% |
-5,64% |
|
Jul |
14,97% |
18,29% |
10,01% |
|
Ago |
-10,86% |
8,78% |
21,23% |
|
Set |
-19,69% |
-23,74% |
-4,16% |
|
Oct |
-16,45% |
-29,02% |
-19,86% |
|
Nov |
0,39% |
-12,69% |
-17,00% |
|
Dic |
-0,34% |
25,69% |
-9,39% |
Fuente: [23]
La rentabilidad de cada cultivo (cuadro 2), medida como la utilidad bruta generada por hectárea cosechada, se calculó como un producto del rendimiento en kg ha-1 y el precio mensual por kg estimado, menos los costos totales de producción por hectárea.
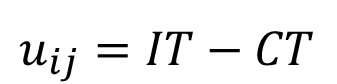 (2)
(2)
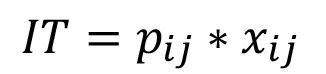 (3)
(3)
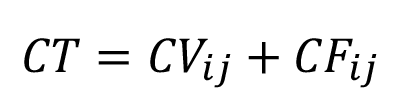 (4)
(4)
Donde,
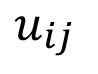 es la rentabilidad bruta por hectárea para el cultivo j en el mes i;
es la rentabilidad bruta por hectárea para el cultivo j en el mes i;
IT es el ingreso total generado por hectárea en base al precio de venta (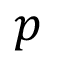 ) por kg y el rendimiento (
) por kg y el rendimiento (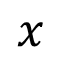 ) en kg cosechados para para el cultivo j en el mes i;
) en kg cosechados para para el cultivo j en el mes i;
CT es la suma de los costos variables (CV) y costos fijos (CF) por hectárea para el cultivo j en el mes i.
Cuadro 2. Rentabilidad mensual (USD) por hectárea según cultivos de papa (Solanum tuberosum L.), cebolla (Allium cepa L.) y zanahoria (Daucus carota L.). Cartago, Costa Rica. 2019.
|
Mes |
Papa |
Cebolla |
Zanahoria |
|||
|
Variable |
Rentabilidad |
Variable |
Rentabilidad |
Variable |
Rentabilidad |
|
|
Ene |
X-PT1 |
7984 |
X-ON1 |
3001 |
X-CA1 |
4880 |
|
Feb |
X-PT2 |
7589 |
X-ON2 |
3704 |
X-CA2 |
4112 |
|
Mar |
X-PT3 |
7963 |
X-ON3 |
6669 |
X-CA3 |
4794 |
|
Abr |
X-PT4 |
9679 |
X-ON4 |
8394 |
X-CA4 |
6635 |
|
May |
X-PT5 |
5080 |
X-ON5 |
6925 |
X-CA5 |
7956 |
|
Jun |
X-PT6 |
3508 |
X-ON6 |
1903 |
X-CA6 |
4968 |
|
Jul |
X-PT7 |
4085 |
X-ON7 |
1087 |
X-CA7 |
3121 |
|
Ago |
X-PT8 |
7084 |
X-ON8 |
3609 |
X-CA8 |
7458 |
|
Set |
X-PT9 |
6954 |
X-ON9 |
9537 |
X-CA9 |
4353 |
|
Oct |
X-PT10 |
7904 |
X-ON10 |
10842 |
X-CA10 |
5131 |
|
Nov |
X-PT11 |
8401 |
X-ON11 |
7252 |
X-CA11 |
3645 |
|
Dic |
X-PT12 |
7938 |
X-ON12 |
3907 |
X-CA12 |
4626 |
Para el desarrollo de este modelo se consideraron los siguientes supuestos:
•Son constantes las productividades promedio en toneladas por hectárea (t ha-1) de cada cultivo.
•Son constantes los costos por hectárea en cada ciclo de producción de los cultivos9.
•Existe acceso a todos los recursos productivos durante todo el año y hay disponibilidad de agua.
•Se puede sembrar en cualquier mes del año.
•Las restricciones del mercado se definen utilizando la proporción de áreas cultivadas de las estadísticas nacionales asumiendo que ellas responden a las preferencias relativas de consumo.
•Se suponen pequeños productores en un ambiente de competencia perfecta que no distorsionan el mercado.
Diseño del modelo
Función de maximización de la rentabilidad
Para cumplir con la maximización de la rentabilidad, la función objetivo (ecuación 5) estima la utilidad bruta a partir de las ventas esperadas del total de kg cosechados de cada cultivo durante las etapas productivas y los costos totales de establecimiento, mantenimiento y cosecha. La función objetivo se asocia a la maximización de la utilidad bruta de una finca promedio de 2,3410 ha [1], con los tres cultivos mencionados.
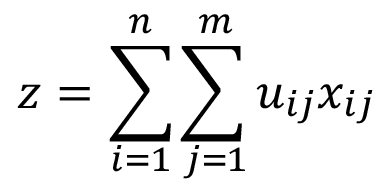
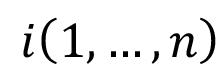
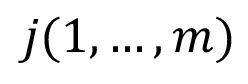 (5)
(5)
Donde, 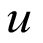 representa la utilidad bruta por hectárea para el cultivo j en el mes i; y
representa la utilidad bruta por hectárea para el cultivo j en el mes i; y 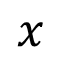 es la cantidad de hectáreas sembradas para el cultivo j en el respectivo mes
es la cantidad de hectáreas sembradas para el cultivo j en el respectivo mes 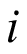 ; siendo m la cantidad de productos y n la cantidad de periodos.
; siendo m la cantidad de productos y n la cantidad de periodos.
Restricciones de área
Sea el área disponible total la siguiente:
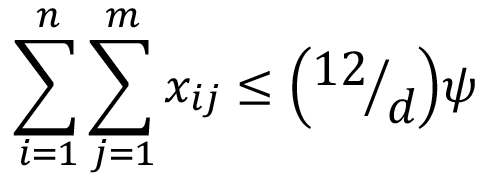
 (6)
(6)
Donde, xij es el área para el cultivo j en el mes i; d es la duración del ciclo de cultivo en meses; es el área promedio de la finca, que en este caso es de 2,34 ha.
Sea el área disponible en rotación de cultivos la siguiente:
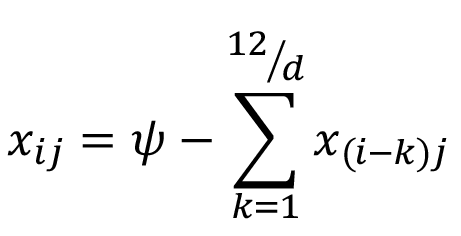 (7)
(7)
Donde, k es el mes rezagado desde el primer mes anterior hasta cumplir con los meses que conforman el ciclo dentro del año de producción; X(i-k)j es el área disponible para sembrar en el mes i menos el área sembrada en los meses anteriores de acuerdo con el ciclo de cultivo.
Es decir, el modelo se restringe a la utilización de esta área sembrada en cada mes del año; y dado que el ciclo productivo es de cuatro meses para cada cultivo, el área disponible para sembrar en el segundo mes debe ser menor o igual al área disponible total menos el área sembrada en el primer mes y sucesivamente hasta el mes en que se cumple cada ciclo.
Restricción de no negatividad
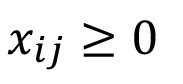 (8)
(8)
Esta restricción impide que, por motivos matemáticos, el área xij destinada para el cultivo j en el mes i, sea menor que cero.
Restricciones de mercado
En el periodo 2007-2017, de las hectáreas sembradas por las fincas de la zona de estudio es aproximadamente del 50% para papa, 26% para cebolla y 24% para zanahoria. Este promedio obtenido a partir de datos anuales, es de acuerdo con el porcentaje de participación relativa del total de hectáreas para los tres cultivos. Tomándose éste comportamiento de siembra como la preferencia revelada del mercado, se utilizó como variable restrictiva para el modelo [25].
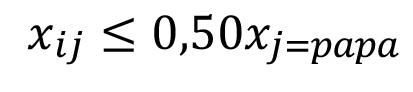 (9)
(9)
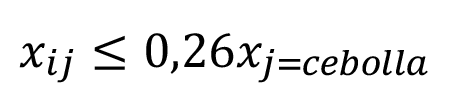 (10)
(10)
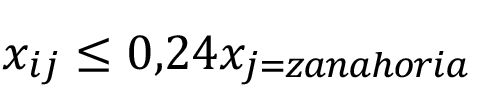 (11)
(11)
Restricción de capital anual
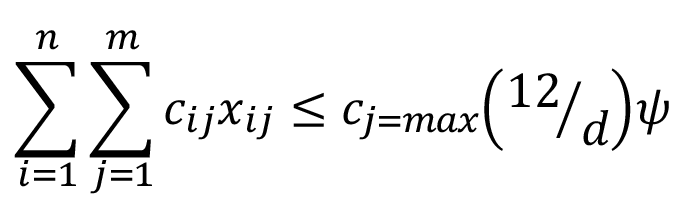
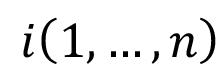
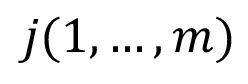 (12)
(12)
Donde, cij es el costo de producción para el cultivo j en el mes i; cj=max es el costo de producción más alto de los cultivos involucrados.
El modelo no incluye costo financiero, pero si la restricción presupuestaria anual. Además, se utilizó el complemento Solver de la suite ofimática de Microsoft Excel para obtener la solución del modelo de PL para maximizar la rentabilidad de una finca de 2,34 ha, destinada a los cultivos de interés en tres ciclos de producción anual (cuatro meses cada ciclo).
Resultados y Discusión
Como se observa en el cuadro 2, una hectárea de cebolla genera la rentabilidad más alta y la más baja, en los meses de octubre y julio según corresponde. El cultivo de papa por su parte, presenta las utilidades más altas en todo el año de manera sostenida, por encima de la cebolla y la zanahoria.
Las soluciones óptimas maximizaron la rentabilidad del productor en los meses en que existe un mayor índice de estacionalidad de los precios, y desechó las épocas donde el comportamiento del índice es menor, por ejemplo, si el terreno se dedica únicamente a la producción de papa, cultivar en abril permitirá al productor aprovechar los precios del mes de julio, donde se presenta el mayor índice de precios, y evitará la cosecha en los meses en que existen los menores índices de precios (cuadro 1). La utilidad se maximizó en 46846 USD, con el uso del 89% del presupuesto total disponible para estos cultivos (cuadro 3).
Cuadro 3. Parámetros de maximización de la utilidad para la rotación de los cultivos de papa (Solanum tuberosum L.), cebolla (Allium cepa L.) y zanahoria (Daucus carota L.). Cartago, Costa Rica. 2019.
|
Cultivo |
Utilidad anual (USD) |
Presupuesto utilizado |
Hectáreas utilizadas |
Meses de siembra |
|
Papa |
28900 |
51% |
3,51 |
Abr-Ago-Dic |
|
Cebolla |
9680 |
24% |
1,83 |
Abr-Ago-Dic |
|
Zanahoria |
8266 |
14% |
1,68 |
Abr-Ago-Dic |
|
Total |
46846 |
89% |
7,02 |
La solución del modelo mantiene bajo cultivo las 2,34 ha disponibles con un aprovechamiento total anual de 7,02 ha, lo anterior, debido a que dicha área se siembra varias veces durante el año.
La restricción de preferencia de mercado obliga a la solución a mantener la composición de proporcionalidad de oferta de los tres cultivos en las proporciones de 50% para papa, 26% cebolla y 24% zanahoria. Por lo tanto, se siembran en esta proporción cada vez que se realiza una siembra, esta restricción pretende contemplar la concentración de mercado, ya que si el productor siembra todo en un único periodo, los demás meses estarían desabastecidos y probablemente el índice de precios cambiaría por el impacto de la producción en el mercado.
Los resultados de rentabilidad generada por cada cultivo en el mes respectivo de siembra se resumen en el cuadro 4.
Cuadro 4. Resultados del modelo de programación lineal (PL) por cultivo de papa (Solanum tuberosum L.), cebolla (Allium cepa L.) y zanahoria (Daucus carota L.). Cartago, Costa Rica. 2019.
|
Cultivo |
Mes de siembra |
Mes de cosecha |
Uso de área (ha) |
Rentabilidad (USD) |
|
Papa |
Abr |
Jul |
1,17 |
11325 |
|
Ago |
Dic |
1,17 |
8288 |
|
|
Dic |
Mar |
1,17 |
9288 |
|
|
Cebolla |
Abr |
Jul |
0,61 |
5107 |
|
Ago |
Dic |
0,61 |
2196 |
|
|
Dic |
Mar |
0,61 |
2377 |
|
|
Zanahoria |
Abr |
Jul |
0,56 |
3726 |
|
Ago |
Dic |
0,56 |
1942 |
|
|
Dic |
Mar |
0,56 |
2598 |
El modelo supone que el productor tiene acceso al capital para la siembra, en este sentido, es importante mencionar que el mes de abril es el que genera mayor rentabilidad al productor y en el mes de julio se daría el mayor flujo de caja, razón por la cual, las opciones de financiamiento que tomen deberían contemplar la capacidad de pago con base en estos ciclos.
Cuadro 5. Resumen de rentabilidad (USD) según mes de siembra de papa (Solanum tuberosum L.), cebolla (Allium cepa L.) y zanahoria (Daucus carota L.). Cartago, Costa Rica. 2019.
|
Cultivo |
Mes de siembra |
Total |
||
|
Abril |
Agosto |
Diciembre |
||
|
Papa |
11325 |
8288 |
9288 |
28900 |
|
Cebolla |
5107 |
2196 |
2377 |
9680 |
|
Zanahoria |
3726 |
1942 |
2598 |
8266 |
|
Total |
20158 |
12425 |
14263 |
46846 |
|
Participación |
43,03% |
26,52% |
30,45% |
|
En un segundo escenario, si el productor deseara producir los tres cultivos durante un año productivo, sin la restricción de preferencias del mercado, la solución óptima da como resultado una maximización de la utilidad bruta que ascendió a 59616 USD, con menor uso de presupuesto (84%) y se aprovecha el 100% del área disponible. El sistema responde a una sola siembra de papa en el mes de enero, una de cebolla en el mes de setiembre, y una de zanahoria en mayo.
Cuadro 6. Parámetros de maximización de la utilidad para la rotación de los cultivos de papa (Solanum tuberosum L.), cebolla (Allium cepa L.) y zanahoria (Daucus carota L.), sin restricción de mercado. Cartago, Costa Rica. 2019.
|
Cultivo |
Utilidad anual (USD) |
Presupuesto utilizado |
Hectáreas utilizadas |
Mes de siembra |
Mes de cosecha |
|
Papa |
18684 |
34% |
2,34 |
Ene |
Abr |
|
Cebolla |
22316 |
31% |
2,34 |
Set |
Dic |
|
Zanahoria |
18616 |
20% |
2,34 |
May |
Ago |
|
Total |
59616 |
84% |
7,02 |
|
|
Resulta importante destacar que este modelo de optimización no establece de previo el plan de siembra como Alvarado-Boirivant [15], por lo que las fechas de siembra se obtienen con el resultado de la optimización que responde a la rentabilidad por hectárea esperada en cada mes del año.
El modelo asignó mayor área de siembra al cultivo de la papa, por presentar mejor rentabilidad relativa y menos a los otros dos cultivos, además el modelo seleccionó los meses de abril, agosto y diciembre, con la finalidad de que la cosecha se obtenga en los meses posteriores en donde se presentan los mejores precios de mercado. Lo anterior debido a que la estacionalidad de los precios en Costa Rica y el comportamiento del consumidor en la compra han marcado el índice de precios de manera que el productor conoce la mejor época de siembra y cosecha de los mismos, tratando siempre de mantener oferta de los tres productos. Esta consideración de la dinámica de precios coincide con resultados de investigaciones similares como las realizadas por Alvarado-Boirivant [15] y Ahumada y Villalobos [26].
El área total anual optimizada corresponde a la suma de los tres ciclos de los cultivos interactuando en el tiempo, de manera que el modelo capturó la dinámica multiciclo de forma similar a Galán et al. [27] en España, con la diferencia que, en este caso, el resultado de un ciclo para un cultivo no es considerado para el ciclo sucesivo.
En su trabajo, Filippi et al. [28] también consideraron la dinámica de precios de mercado, pero difiere de esta investigación particularmente en que utilizaron restricciones sobre ventanas en el año para realizar actividades de siembra, cuando en esta investigación no fue así, ya que se permitió el acceso al riego para poder cultivar en cualquier época del año.
El segundo modelo aplicado sin restricciones de mercado, resuelve sembrar toda el área disponible una sola vez en el año para cada cultivo y así obtener una mayor utilidad, de la misma manera que Morales y Murcia [29]. No obstante, se considera importante ampliar este modelo a otros cultivos con ciclos distintos para analizar el efecto correspondiente a las diferencias de ciclo, como fue planteado por Mohamad y Said [12].
Conclusiones
El modelo matemático de programacion lineal, en el primer escenario permitió demostrar que la optimización económica del sistema de rotación productiva de los cultivos de papa (PT), cebolla (ON) y zanahoria (CA), se alcanzó al sembrarlos en los meses de abril, agosto y setiembre, para cosechar en los meses de julio, noviembre y diciembre. Esto siempre que se imponga una restricción de preferencia de mercado que obliga a respetar una proporcionalidad en la oferta de los cultivos.
Las restricciones de mercado utilizadas, facilitan la distribución de la rotación de siembra, sin embargo, genera que todos los productores trabajen igual y que no haya diferencias en las épocas de cosecha entre productores. Al ser productos poco influenciados por la importación, el mercado de precios se rige mayormente en función de la oferta nacional.
En un segundo escenario donde no existe esta restricción de mercado, el modelo busca maximizar en el mes en todo el año en donde prevalezcan los mejores precios. De ésta manera se utiliza la totalidad de la tierra disponible para un solo cultivo cada vez que se siembra, sea enero para papa, setiembre para cebolla y mayo para zanahoria y así aprovechar de una mejor forma el precio de mercado.
La solución de mayor rentabilidad se presentó en el segundo escenario, en donde los productores siembran una sola vez al año cada cultivo, y utilizan toda la tierra disponible. No obstante, esto puede generar un mayor riesgo de que si todos los productores se comportan de la misma manera, y se genere un exceso de oferta en un mismo momento que provoque una caída de precios, lo anterior, ante una realidad donde no hay mecanismos de almacenamiento del producto para distribuir esa cosecha durante el año. Se presume entonces, que sembrar más en un solo momento, genera un mayor riesgo, por lo que el segundo modelo estaría siendo más riesgoso que el primero, situación que podría evaluarse si se incluyen variables de riesgo al modelo, lo cual está fuera del alcance de este trabajo.
Referencias
[1] INEC (Instituto Nacional de Estadística y Censos), Cultivos agrícolas, forestales y ornamentales. San José, Costa Rica: INEC, 2015.
[2] M. Osaki y M. O. Batalha, «Optimization model of agricultural production system un grain farms under risk, in Sorriso, Brazil», Agric. Syst., vol. 127, pp. 178-188, 2014, doi: 10.1016/j.agsy.2014.02.002.
[3] B. Render, R. M. Stair, y M. E. Hanna, Métodos cuantitativos para los negocios, 11.a ed. México: Pearson Education, 2012.
[4] K. Mathur y D. Solow, Investigación de operaciones: El arte de la toma de decisiones. México: Prentice-Hall, 1996.
[5] T. El-Nazer y B. A. McCarl, «The choice of crop rotation: A modeling approach and case study», Am. J. Agric. Econ., vol. 68, n.o 1, pp. 128-136, 1986, doi: 10.2307/1241657.
[6] P. Paam, R. Berretta, M. Heydar, R. H. Middleton, R. García-Flores, y P. Juliano, «Planning models to optimize the agri-fresh food supply chain for loss minimization: A review», CSIRO Res. Publ. Repos., pp. 1-16, 2016, doi: 10.1016/B978-0-08-100596-5.21069-X.
[7] R. J. Lora-Freyre y R. G. Pellicer-Durán, «Maximización de la producción de café a través de la programación lineal», Anu. Fac. Cienc. Económicas Empres., vol. 3, pp. 61-70, 2012.
[8] M. Bedoya-Cardoso y R. Salazar-Moreno, «Optimización del uso de fertilizantes para el cultivo de café», Rev. Mex. Cienc. Agríc., vol. 5, pp. 1433-1439, 2014, doi: 10.29312/remexca.v0i8.1100.
[9] W. A. Miller, L. C. Leung, T. M. Azhar, y S. Sargent, «Fuzzy production planning model for fresh tomato packing», Int. J. Prod. Econ., vol. 53, pp. 227-238, 1997, doi: 10.1016/S0925-5273(97)00110-2.
[10] J. A. Herrera, A. García, y J. Suárez, «Análisis prospectivo de la base alimentaria en una lechería tropical con programación lineal», Pastos Forrajes, vol. 37, pp. 435-441, 2014.
[11] D. Ortega-Gaucin, E. Mejía-Sáenz, E. Palacios-Vélez, L. Rendón-Pimentel, y A. Excebio-García, «Modelo de optimización de recursos para un distrito de riego», Terra Latinoam., vol. 27, n.o 3, pp. 219-226, 2009.
[12] N. H. Mohamad y F. Said, «A mathematical programming approach to crop mix problem», Afr. J. Agriculytural Res., vol. 6, n.o 1, pp. 191-197, 2011, doi: 10.5897/AJAR10.028.
[13] J. Jebelli, B. Paterson, y A. Abdelwahab, «A linear programming model to optimize cropping pattern in small-scale irrigation schemes: an application to Mekabo Scheme in Tigray, Ethiopia», Int. J. Environ. Agric. Res., vol. 2, n.o 8, pp. 24-34, 2016.
[14] L. W. Tauer, «Target MOTAD», Am. J. Agric. Econ., vol. 65, pp. 606-610, 1983, doi: 10.2307/1240515.
[15] J. A. Alvarado-Boirivant, «La programación lineal aplicación de la pequeñas y medianas empresas», Rev. Reflex., vol. 88, n.o 1, pp. 89-105, 2009.
[16] J. A. Alvarado-Boirivant, «El análisis post-optimal en programación lineal aplicada a la agricultura», Rev. Reflex., vol. 90, n.o 1, pp. 161-173, 2011.
[17] J. A. Alvarado-Boirivant, «Modelo de optimización para un asentamiento agrícola en La Cruz de Guanacaste, Costa Rica», Rev. InterSedes, vol. 14, n.o 29, pp. 19-40, 2013.
[18] F. S. Hillier y G. J. Lieberman, Introducción a la investigación de operaciones, 9.a ed. México: McGraw-Hill, 2010.
[19] D. R. Anderson, D. J. Sweeney, y T. A. Williams, Métodos cuantitativos para los negocio, 9.a ed. México: Thomson, 2004.
[20] InfoAgro, «Costos de producción de papa», MAG (Ministerio de Agricultura y Ganadería), 2015. http://www.infoagro.go.cr/EstadisticasAgropecuarias/CostosProduccion/Paginas/default.aspx.
[21] InfoAgro, «Costos de producción de zanahoria», MAG (Ministerio de Agricultura y Ganadería), 2015. http://www.infoagro.go.cr/EstadisticasAgropecuarias/CostosProduccion/Paginas/default.aspx.
[22] InfoAgro, «Costos de producción de cebolla», MAG (Ministerio de Agricultura y Ganadería), 2018. http://www.infoagro.go.cr/EstadisticasAgropecuarias/CostosProduccion/Paginas/default.aspx.
[23] PIMA (Programa Integral de Mercadeo Agropecuario), «Calendario de estacionalidad hortalizas 2018», PIMA, 2018. http://www.pima.go.cr/wp-content/uploads/2018/07/Calendario-de-estacionalidad.pdf.
[24] PIMA (Programa Integral de Mercadeo Agropecuario), «Boletín de precios por fecha», PIMA, 2019. http://www.pima.go.cr/simm/.
[25] FAOSTAT, «Datos sobre alimentación y agricultura», FAO (Food and Agriculture Organization of the United Nations), 2019. http://www.fao.org/faostat/en/.
[26] O. Ahumada y J. R. Villalobos, «Operational model for planning the harvest and distribution of perishable agricultural products», Int. J. Prod. Econ., vol. 133, pp. 677-687, 2011, doi: 10.1016/j.ijpe.2011.05.015.
[27] A. Galán, C. Pozo, G. Guillén-Gosálbez, A. Antón, y L. Jiménez, «Multi-stage linear programming model for optimizing cropping plan decisions under the new Common Agricultural Policy», Land Use Policy, vol. 48, pp. 515-524, 2015, doi: 10.1016/j.landusepol.2015.06.022.
[28] C. Filippi, R. Mansini, y E. Stevanato, «Mixed integer linear programming models for optimal crop selection», Comput. Oper. Res., vol. 81, pp. 26-39, 2017, doi: 10.1016/j.cor.2016.12.004.
[29] E. Morales y H. H. Murcia, «Aplicación de la programación simplificada en una finca de San Rafael de Alajuela», Agron. Costarric., vol. 1, n.o 1, pp. 5-15, 1977.
1 Este trabajo formó parte del proyecto de investigación 822-B7-518 del Centro de Investigaciones en Economía Agrícola y Desarrollo Agroempresarial (CIEDA).
2 Bach. Economía Agrícola y Agronegocios, Centro de Investigaciones en Economía Agrícola y Desarrollo Agroempresarial (CIEDA), Universidad de Costa Rica (UCR), Costa Rica. Correo electrónico: josdavbn@gmail.com https://orcid.org/0000-0002-5444-3814
https://orcid.org/0000-0002-5444-3814
3 ME. Economía Empresarial, CIEDA, UCR, Costa Rica. Correo electrónico: johanna.solorzano@ucr.ac.cr.  https://orcid.org/0000-0002-0276-6849
https://orcid.org/0000-0002-0276-6849
4 M.Sc. Administración y Dirección de Empresas, CIEDA, UCR, Costa Rica. Correo electrónico: javier.paniagua@ucr.ac.cr.  htps://orcid.org/0000-0003-2815-5437
htps://orcid.org/0000-0003-2815-5437
5 Se entiende como zona norte de Cartago, aquellos territorios ubicados en las faldas del volcán Irazú a una altitud superior a 1500 msnm.
6 Minimization of Total Absolute Deviations propuesto por Tauer [14].
7 Programa Integral de Mercadeo Agropecuario.
8 Entiéndase índice estacional de precios como la variación en cada mes con respecto al precio promedio anual.
9 Tres ciclos por año.
10 Área promedio de fincas de la zona norte de Cartago [1].