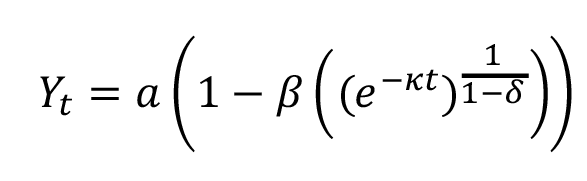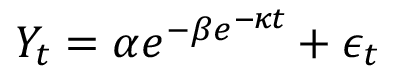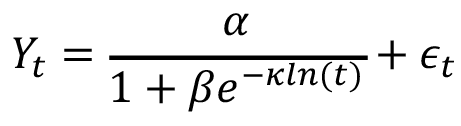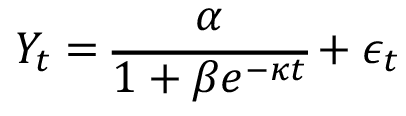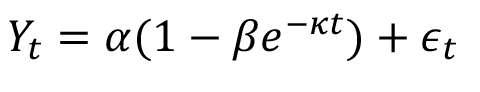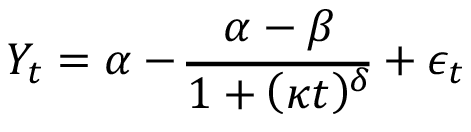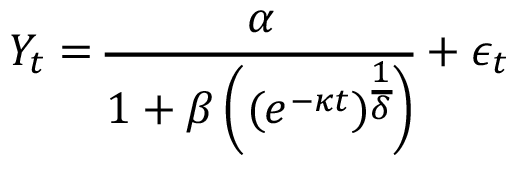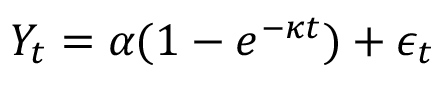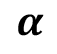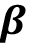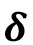Ajuste de diferentes modelos de crecimiento no lineal al rendimiento de la palma aceitera (Elaeis guineensis) a lo largo del ciclo de vida del cultivo, Costa Rica

Fitting different nonlinear growth models to oil palm (Elaeis guineensis) yield along the crop lifecycle, Costa Rica

Johanna Solórzano-Thompson1, Javier Paniagua-Molina2,
David Barboza-Navarro3

Fecha de recepción: 3 de abril de 2020
Fecha de aprobación: 30 de julio de 2020

Solórzano-Thompson, J; Paniagua-Molina, J;
Barboza-Navarro, D. Ajuste de diferentes modelos de crecimiento no lineal al rendimiento de la palma aceitera (Elaeis guineensis) a lo largo del ciclo de vida del cultivo, Costa Rica. Tecnología en Marcha. Vol. 34-1. Enero-Marzo 2021. Pág 115-126.

https://doi.org/10.18845/tm.v34i1.5096

Palabras clave

Transformación de Box-Cox; eficiencia del pronóstico; regresión no lineal; aceite de palma; ciclo de vida del cultivo.

Resumen

Esta investigación se enfocó en el cultivo de palma aceitera en la zona sur de Costa Rica, por el alto impacto que genera en el desarrollo económico de agricultores costarricenses. Se ajustó la curva de crecimiento del rendimiento de la palma aceitera a lo largo del ciclo de vida del cultivo y se comparó la eficiencia de pronóstico de ocho modelos de crecimiento no lineal con base en diferentes criterios estadísticos y pruebas de normalidad. Posteriormente, se aplicó el método de transformación Box-Cox para corregir la ausencia de normalidad en los residuos. Los modelos no lineales aplicados fueron adecuados para pronosticar el rendimiento de palma aceitera; el modelo Morgan-Mercer-Flodin produjo las mejores estadísticas de ajuste. Esta investigación constituye un insumo para las prácticas de renovación de plantaciones, así como para la valoración económica de cultivos que se prendan como garantía bancaria.

Keywords

Box-Cox transformation; forecast efficiency; nonlinear regression; palm oil; crop life cycle.

Abstract

This research focused on the oil palm crop in the southern zone of Costa Rica due to the high impact it generates on the economic development of Costa Rican farmers. The oil palm yield growth curve was adjusted along the crop life cycle, and the forecast efficiency of eight nonlinear growth models was compared based on different statistical criteria and normality tests. Then the Box-Cox transformation method was applied to correct the absence of normality. The applied nonlinear models were adequate to forecast oil palm yield, and the Morgan-Mercer-Flodin model produced the best fit statistics. This research constitutes an input for plantation renovation practices, as well as the economic valuation of crops that may be pledged as collaterals.

Introducción

La industria de la palma aceitera (Elaeis guineensis) es participe del mercado mundial de aceites y grasas. De octubre de 2018 a septiembre de 2019, el consumo mundial de aceite de palma aumentó en 7,8 t, y América Latina contribuyó con 5,8% de la producción mundial en el mismo periodo [1]. Este crecimiento ha fomentado un avance en el desarrollo económico de áreas rurales en países como Colombia, Honduras, Perú, Ecuador, Nicaragua y Costa Rica [2].

En el año 2014 existían en Costa Rica cerca de 2 169 fincas con 66 420 hectáreas cultivadas de palma aceitera, que generaban empleo principalmente en áreas de bajo índice de desarrollo humano [3]. Para el 2018, la palma aceitera representaba el 8,1% de la producción nacional de las principales actividades agrícolas, solo por debajo de los cultivos de caña de azúcar, piña y plátano [4]. Esta información confirma la importancia del cultivo de palma aceitera para la calidad de vida en las zonas rurales, por la generación de empleo asociada a este cultivo, significativa en la lucha contra la pobreza. En Colombia, por ejemplo, los trabajadores del sector de palma aceitera han percibido ingresos diarios seis veces más altos que los ubicados en la línea de pobreza [5].

El C.I.F. Rotterdam es en el mundo uno de los precios de referencia más importantes del aceite de palma crudo y se caracteriza por una alta volatilidad, con ciclos de precios muy bajos en contraste con tiempos de “picos” más altos [6]. El sector de la palma aceitera no solo enfrenta este reto, sino que también está expuesto a los impactos negativos de las plagas y enfermedades. En los últimos cinco años, la producción costarricense se ha visto afectada por la enfermedad conocida como “pudrición del cogollo”, que disminuyó considerablemente la productividad y la entrega de fruta fresca para el procesamiento del aceite [7], [8]. Este hecho, junto con la caída aproximada del 50% en el precio internacional del crudo en diciembre de 2019 en comparación con el año 2012 [9], ha generado un efecto negativo y compromete la estabilidad económica de la industria y de los productores costarricenses.

Con estos impactos negativos, el productor necesita mantener una alta productividad en sus plantaciones para operar de manera eficiente. Esto hace de Costa Rica un escenario clave para el estudio de la dinámica del rendimiento de la palma aceitera a lo largo del ciclo de vida del cultivo, como base para futuras investigaciones que involucren un análisis costo-beneficio para determinar del momento óptimo de renovación de la plantación.

Para calcular las tasas de crecimiento en animales y rendimientos de cultivos, se han utilizado modelos no lineales con tasas de crecimiento proporcionales como el modelo Monomolecular, modelos simétricos y de crecimiento exponencial como el modelo Logistic, y asimétricos, con forma sigmoidea, como el Gompertz y sus derivados [10]–[13].

Por otra parte, se han realizado con frecuencia investigaciones en cultivos de ciclo anual, como el cultivo de cereales en la India, para el que se determinaron tasas de crecimiento de la producción de 2,36% y 2,38% con los modelos Logistic y Gompertz, respectivamente, los cuales se consideraron adecuados para modelar por la bondad del ajuste, según los criterios de Error Cuadrático Medio (MSE) y Error Absoluto Medio (MAE). Por otro lado, se descartó el modelo Monomolecular por presentar un parámetro de capacidad de crecimiento extremadamente alto [14].

La adaptabilidad de cereales como el trigo a diferentes condiciones climáticas ha favorecido su expansión mundial, siendo la India uno de los principales productores y consumidores. En una investigación del año 2014 se utilizaron modelos no lineales para estudiar las tendencias del crecimiento en el área, la producción y la productividad del cultivo de trigo en la India, aunque no fueron lo suficientemente dinámicos de acuerdo con los criterios del coeficiente de determinación (R2) ajustado, el MAE, la Raíz del Error Cuadrático Medio (RMSE) y la normalidad de los residuos [15]. Otro estudio demostró una adaptación correcta de los modelos Logistic, Gompertz y Monomolecular para calcular las tasas de crecimiento del trigo y ajustar el pronóstico de los datos con estadísticas similares proporcionadas por los parámetros MAE, RMSE y Error de Porcentaje Absoluto Medio (MAPE) [16].

También se demostró que los modelos Monomolecular y Logistic presentaron un mejor ajuste que el modelo Gompertz en el rendimiento de maní en India, con respecto a los criterios R2, MAE, RMSE y MAPE. Los resultados mostraron una tasa de crecimiento lenta y constante, y sobresalió la importancia de utilizar modelos no lineales, ya que pueden desempeñar un papel crucial en el desarrollo de políticas agrícolas [17].

Con respecto a la modelación del rendimiento en cultivos perennes, la disponibilidad de estudios no es abundante; esto se debe a la dificultad para obtener y registrar datos precisos en edades avanzadas de la plantación. Existen pocos estudios sobre la curva del rendimiento productivo de la palma aceitera a lo largo de su ciclo de vida, ya que la investigación se ha enfocado en medir el rendimiento productivo en función del índice de cosecha, el área foliar y la densidad de la plantación, además, de factores subyacentes a las brechas de rendimiento, como la incidencia de plagas y enfermedades, la temperatura, la velocidad del viento y la profundidad del suelo [18], [19].

En Malasia, se comprobó el ajuste mediante diferentes modelos no lineales utilizando el rendimiento promedio de racimos de fruta fresca (FFB) de palma aceitera, con una observación para cada año. Los resultados mostraron que el rendimiento productivo aumentó vigorosamente hasta el décimo año después de la siembra y creció de manera constante hasta el vigésimo año. Con las estadísticas MSE, MAE, MAPE y la suma de cuadrados del error, se comprobó que el modelo Logistic ofrecía el mejor ajuste de pronóstico, seguido por los modelos Gompertz, Morgan-Mercer-Flodin, Chapman-Richard y Log-logistic. Los modelos Monomolecular y Exponencial Negativo no fueron apropiados porque no tienen un punto de inflexión ni forma sigmoidea [10].

Los estudios mencionados proporcionan información importante sobre el uso de modelos no lineales en la agricultura y contribuyen a futuras investigaciones sobre el valor económico del negocio. En el caso de la investigación que aquí se trata, se encontró la limitación de acceso a estudios previos de curvas de crecimiento en cultivos perennes como este, porque su larga vida útil (aproximadamente veinticinco años en el caso de la palma) dificulta el registro de datos precisos. Para contribuir con el estudio de curvas de crecimiento en cultivos perennes, el objetivo de esta investigación fue comparar la eficiencia de los pronósticos de diferentes modelos de crecimiento no lineal sobre el rendimiento de la palma aceitera en Costa Rica por medio de la aplicación de diferentes criterios estadísticos y pruebas de normalidad.

Materiales y métodos

El estudio se realizó con productores de palma aceitera en la zona sur de Costa Rica, donde la actividad es de gran impacto en el desarrollo económico de la región. Se realizaron encuestas durante los años 2016 y 2017, con visitas a cada productor en sus respectivas fincas cuando fue posible. El número total de observaciones recolectadas corresponde a 460 fincas, con diferentes áreas de producción y rendimientos por hectárea. La variable dependiente de los modelos fue el rendimiento total anual en toneladas de racimos de fruta fresca por hectárea (FFB/ha) y no se consideró el rendimiento del aceite, ya que el propósito fue modelar el comportamiento en campo de la biomasa de interés económico para el sistema productivo primario. Los datos corresponden a productores con una gestión técnica considerada como promedio para la región en la que se realizó el estudio. El software utilizado para esta investigación fue R-Studio, con sus respectivas bibliotecas para el análisis de regresión no lineal.

Para ajustar la curva de crecimiento del rendimiento de la palma aceitera a través del tiempo, se utilizaron ocho modelos no lineales diferentes (cuadro 1). Posteriormente, se midió la eficiencia de pronóstico de los modelos y se comparó con los criterios estadísticos MAE, MSE, RMSE y MAPE, el logaritmo de máxima verosimilitud o log likelihood (logLik), el Criterio de Información de Akaike (AIC) y el Criterio de Información Bayesiano (BIC). En este caso, para dos o más modelos comparados con estos parámetros, cuanto menor fuera el parámetro obtenido para un modelo dado, mayor era su eficiencia de pronóstico.

Para los modelos del cuadro 1, es el rendimiento total anual en toneladas de FFB/ha de palma aceitera en el momento (años); es el valor asintótico o el potencial máximo esperado de la variable de respuesta; es una constante biológica en la que se alcanza el punto de inflexión de la curva de crecimiento; es la velocidad a la cual la variable de respuesta alcanza su potencial máximo; es una constante de crecimiento alométrico, y es el término de error aleatorio.

Cuadro 1. Modelos de crecimiento no lineal aplicados al rendimiento de la palma aceitera (Elaeis guineensis)

Modelo	Ecuación
Chapman-Richard´s		(1)
Gompertz		(2)
Log-logistic		(3)
Logistic		(4)
Monomolecular		(5)
Morgan-Mercer-Flodin		(6)
Richard´s		(7)
Von Bertalanffy		(8)

Fuente: [10], [20]–[22].

También se aplicaron diferentes pruebas para evaluar la hipótesis de la normalidad de los residuos, como la Jarque-Bera (JB), la Shapiro-Wilk (SW), la Anderson-Darling (AD), la Lilliefors (LF), la Pearson (PS) y la Cramér-von Mises (CM). Para corregir la ausencia de normalidad en la serie de datos original, se aplicó la transformación Box-Cox (ecuación 9), que utiliza un único parámetro “lambda” (λ), que puede tomar diferentes valores (positivos o negativos) para obtener la normalidad deseada en los datos [23].

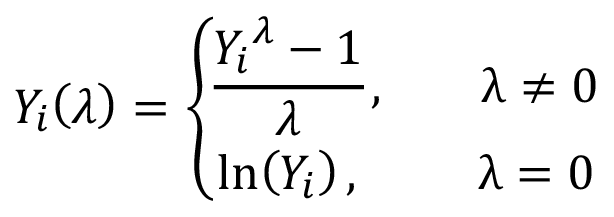(9)

Donde representa la serie de datos original, con , es decir, todos los valores de la serie original deben ser positivos. Para los casos en que , la serie original se trabaja exponencialmente, y cuando se aplica el logaritmo natural a la serie original; sin embargo, este último caso no se presentó en esta investigación.

Resultados y discusión

En este estudio, se consideró a Khamis et al. [10] como el principal referente para el modelado de la curva de rendimiento en palma aceitera, con la salvedad de que un mayor número de variables independientes en los modelos no lineales hizo más compleja su modelación. Además, la principal diferencia con el presente estudio fue que los datos utilizados en dicha investigación correspondían a una observación del rendimiento por año en un periodo definido y provenían de fuentes secundarias.

La curva de crecimiento del rendimiento de palma aceitera obtenida (figura 1) coincide con Khamis et al. y Woittiez et al. [10], [19], quienes describieron un crecimiento vigoroso en la producción hasta el décimo año después de la siembra y una etapa estable hasta el vigésimo año. Se puede observar una etapa de disminución en la producción después de alcanzar el máximo potencial productivo, que se obtuvo cerca del duodécimo año, con un rendimiento que oscila entre 25 y 30 t de FFB/ha.

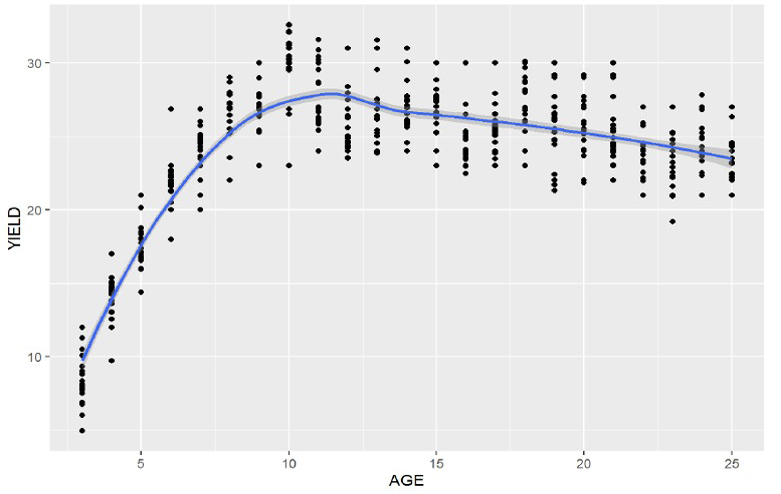
Figura 1. Curva de crecimiento del rendimiento anual total de palma aceitera (Elaeis guineensis) en toneladas de racimos de fruta fresca por hectárea (FFB/ha).

Los resultados de la modelación muestran significancia estadística para la mayoría de los parámetros de los modelos no lineales aplicados (cuadro 2). Los modelos Logistic y Richard´s presentaron los criterios de eficiencia de pronóstico más bajos (MAE, MSE, RMSE, MAPE, logLik, AIC y BIC), al contrario del modelo von Bertalanffy, que presentó los parámetros más altos. No obstante, no se puede asumir el supuesto de normalidad, pues al menos en cinco de las pruebas aplicadas se rechazó la hipótesis nula para cada modelo.

Después de aplicar la trasformación Box-Cox (cuadro 3) a la serie de datos original de FFB, se obtuvo una mejora generalizada en la eficiencia de pronóstico de todos los modelos. El modelo Morgan-Mercer-Flodin probó la mayor eficiencia de pronóstico, a excepción de los criterios AIC y BIC, aunque la hipótesis de normalidad se rechazó con las pruebas SW, AD, PS y CM, con un nivel de significancia estadística del 5%. Los modelos que le siguieron en eficiencia de pronóstico fueron el Richard´s, el Gompertz, el Log-logistic y el Logistic.

Con respecto a la normalidad de los residuos, se rechazó la hipótesis nula para los modelos Monomolecular, von Bertalanffy y Morgan-Mercer-Flodin, con al menos dos pruebas aplicadas, aunque con la prueba Jarque-Bera, se obtuvo normalidad en todos los casos, a excepción del modelo von Bertalanffy, para el cual se rechazó la hipótesis de normalidad bajo un nivel de significancia estadística de 0,1%.

Cuadro 2. Resultados de la modelación del rendimiento de palma aceitera (Elaeis guineensis) sin transformación Box-Cox.

Modelo no lineal sin Box-Cox			Parámetro				MAE	MSE	RMSE	MAPE	logLik	AIC	BIC	JB	SW	AD	LF	PS	CM
Chapman-Richard´s .		Parámetro	25,96	9,9e-04	0,69	1,00	1,88	5,56	2,36	0,08	-1047,00	2105,00	2126,00	7,77	0,99	1,50	0,04	45,57	0,21
		Error Estnd	0,13	0,14	0,04	0,01
		Valor p	<2e-16	0,99	<2e-16	<2e-16								0,02	1,9e-03	7,2e-04	0,07	1,5e-03	3,5e-03
			***		***	***								*	**	***		**	**
Gompertz		Parámetro	25,96	9,70	0,69		1,88	5,56	2,36	0,08	-1047,00	2103,00	2119,00	7,77	0,99	1,50	0,04	45,57	0,22
		Error Estnd.	0,13	1,46	0,04
		Valor p	<2e-16	9,08e-11	<2e-16									0,02	1,9e-03	7,2e-04	0,07	1,5e-03	3,5e-03
			***	***	***									*	**	***		**	**
Log-Logistic		Parámetro	26,01	250,51	4,13		1,94	5,88	2,43	0,09	-1060,00	2129,00	2145,00	8,14	0,99	1,49	0,04	37,74	0,20
		Error Estnd.	0,14	80,73	0,23
		Valor p	<2e-16	2e-03	<2e-16									0,02	1,9e-03	7,5e-04	0,08	0,01	6,1e-03
			***	**	***									*	**	***		*	**
Logistic		Parámetro	25,94	28,91	0,86		1,85	5,41	2,33	0,08	-1041,00	2090,00	2106,00	7,22	0,99	1,39	0,04	52,66	0,20
		Error Estnd.	0,13	6,00	0,05
		Valor p	<2e-16	1,98e-06	<2e-16									0,03	2,9e-03	1,3e-03	0,15	1,5e-04	6,1e-03
			***	***	***									*	**	**		***	**
Monomolecular		Parámetro	25,97	3,57	0,54		1,94	5,88	2,43	0,09	-1060,00	2129,00	2145,00	8,96	0,99	1,69	0,04	37,95	0,26
		Error Estnd.	0,14	0,38	0,03
		Valor p	<2e-16	<2e-16	<2e-16									0,01	1,1e-03	2,5e-04	0,05	0,01	1,1e-03
			***	***	***									*	**	***	*	*	**
Morgan-Mercer-Flodin		Parámetro	25,93	8,05	0,21	6,22	1,88	5,51	2,35	0,08	-1045,00	2100,00	2121,00	8,00	0,99	1,50	0,04	49,32	0,23
		Error Estnd.	0,13	0,84	0,01	0,67
		Valor p	<2e-16	<2e-16	<2e-16	<2e-16								0,02	2,1e-03	7e-04	0,05	4,5e-04	2,2e-03
			***	***	***	***								*	**	***	*	***	**
Richard´s		Parámetro	25,83	20,44	122,93	158,17	1,83	5,35	2,31	0,08	-1039,00	2087,00	2108,00	7,97	0,99	1,75	0,04	75,83	0,25
		Error Estnd.	0,12	5,45	5,46	10,42
		Valor p	<2e-16	2e-04	<2e-16	<2e-16								0,02	7,7e-04	1,7e-04	0,05	4e-08	1,5e-03
			***	***	***	***								*	***	***	*	***	**
Von Bertalanffy		Parámetro	25,54		0,85		2,15	7,08	2,66	0,10	-1103,00	2212,00	2224,00	4,12	0,99	1,25	0,05	55,06	0,21
		Error Estnd.	0,13		0,01
		Valor p	<2e-16		<2e-16									0,13	0,02	2,9e-03	5,3e-03	6,9e-05	3,6e-03
			***		***										*	*	**	***	**

Nota: * representa significancia estadística al 5%; **, al 1%; ***, al 0,1%.

Cuadro 3. Resultados de la modelación del rendimiento de palma aceitera (Elaeis guineensis) con transformación Box-Cox.

Modelo no lineal con Box-Cox		Parámetro				MAE	MSE	RMSE	MAPE	logLik	AIC	BIC	JB	SW	AD	LF	PS	CM
Chapman-Richard´s	Parámetro	5,02	1,8e-03	0,70	1,00	19,22	390,05	19,75	0,79	44,70	-79,40	-58,70	1,11	1,00	0,62	0,03	28,34	0,09
	Error Estnd.	0,01	0,52	0,03	0,11
	Valor p	<2e-16	1,00	<2e-16	<2e-16								0,58	0,23	0,10	0,35	0,13	0,18
		***		***	***
Gompertz	Parámetro	5,46	5,15	0,70		18,81	373,92	19,34	0,78	-19,40	46,80	63,40	0,64	1,00	0,66	0,03	29,81	0,09
	Error Estnd.	0,01	0,55	0,03
	Valor p	<2e-16	<2e-16	<2e-16									0,73	0,22	0,08	0,27	0,10	0,16
		***	***	***
Log-Logistic	Parámetro	5,53	46,06	3,54		18,76	372,14	19,29	0,77	-47,20	102,00	119,00	1,85	1,00	0,73	0,03	35,76	0,11
	Error Estnd.	0,02	8,61	0,15
	Valor p	<2e-16	1,4e-07	<2e-16									0,40	0,18	0,06	0,56	0,02	0,08
		***	***	***													*
Logistic	Parámetro	4,75	8,37	0,80		19,47	400,07	20,00	0,80	90,40	-173,00	-156,00	1,85	1,00	0,60	0,03	35,757	0,08
	Error Estnd.	0,01	1,02	0,03
	Valor p	<2e-16	2,4e-15	<2e-16									0,40	0,19	0,12	0,31	0,02	0,20
		***	***	***													*
Monomolecular	Parámetro	4,76	2,80	0,61		19,47	400,11	20,00	0,80	82,00	-156,00	-139,00	1,96	1,00	0,65	0,04	37,22	0,09
	Error Estnd.	0,01	0,25	0,03
	Valor p	<2e-16	<2e-16	<2e-16									0,37	0,16	0,09	0,05	0,02	0,15
		***	***	***												*	*
Morgan-Mercer-Flodin	Parámetro	11,22	4,05	0,22	5,73	13,49	195,34	13,98	0,55	-533,00	1076,00	1097,00	3,91	0,99	1,03	0,04	33,25	0,16
	Error Estnd.	0,04	0,36	6,1e-03	0,56
	Valor p	<2e-16	<2e-16	<2e-16	<2e-16								0,14	0,03	0,01	0,13	0,04	0,02
		***	***	***	***									*	*		*	*
Richard´s	Parámetro	6,64	7,15	149,03	218,09	17,67	330,97	18,19	0,73	-189,00	389,00	409,00	0,05	0,99	0,65	0,03	37,53	0,09
	Error Estnd.	0,02	1,87	6,45	17,52
	Valor p	<2e-16	1,5e-04	<2e-16	<2e-16								0,98	0,09	0,09	0,20	0,02	0,14
		***	***	***	***												*
Von Bertalanffy	Parámetro	4,97		1,00		19,22	390,38	19,76	0,79	-27,30	60,60	73,00	9,40	0,99	0,64	0,03	48,07	0,10
	Error Estnd.	0,01		0,01
	Valor p	<2e-16		<2e-16									9,1e-03	0,07	0,10	0,27	6,7e-04	0,13
		***		***									***				***

Nota: * representa significancia estadística al 5%; **, al 1%; ***, al 0,1%.

La curva de crecimiento ya ajustada obtenida con cada modelo, para medir el rendimiento de la palma aceitera en la zona sur de Costa Rica, se muestra en la figura 2. También se proporcionan los pronósticos aceptables para cada modelo no lineal después de la transformación Box-Cox y un promedio de todos los modelos en la tabla 4. Estas predicciones simulan el rendimiento de la palma aceitera en FFB/ha en un periodo de 25 años, asumiendo que en el primer y el segundo año después del establecimiento del cultivo el rendimiento en la producción de FFB es nulo.

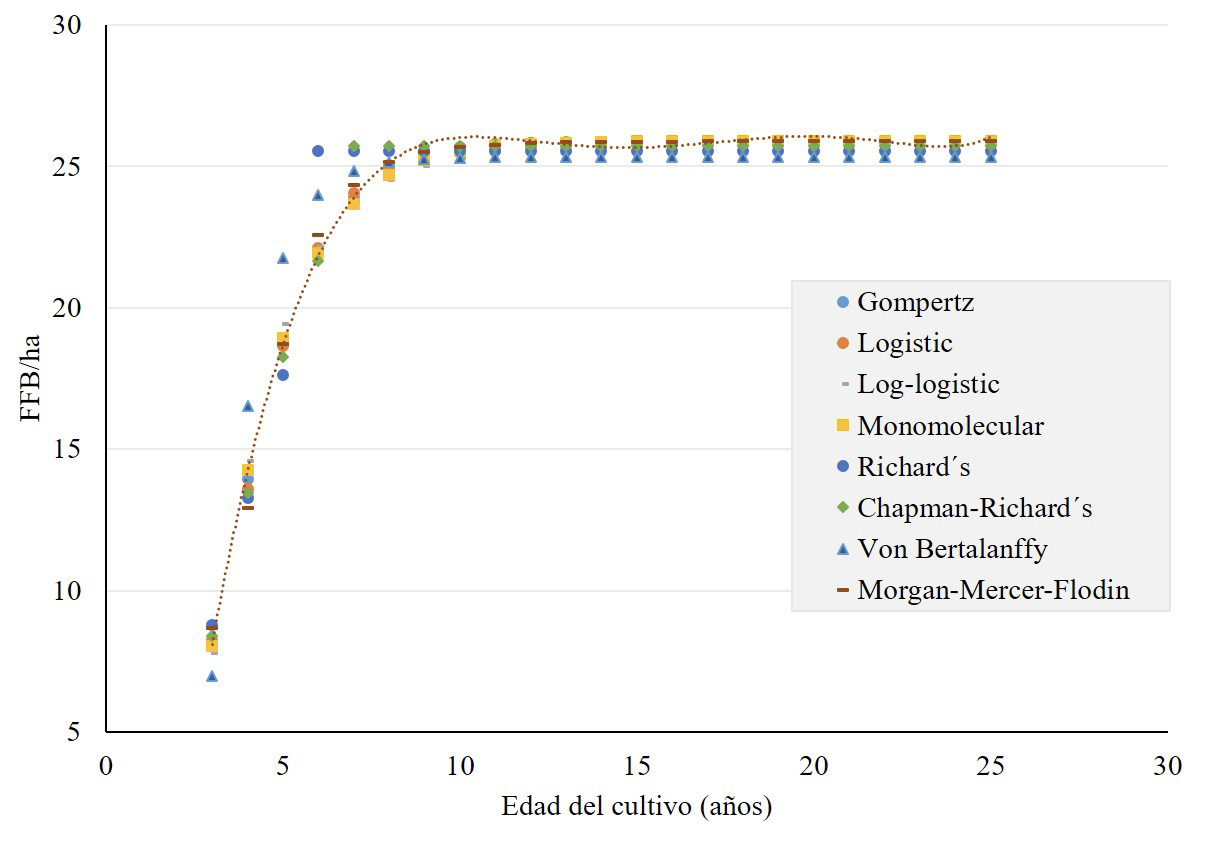
Figura 2. Curvas de ajuste del rendimiento de palma aceitera (Elaeis guineensis) en toneladas de racimos de fruta fresca por hectárea (FFB/ha) para cada modelo no lineal con transformación Box-Cox.

Las predicciones de los modelos son razonables en un periodo de 25 años. Sin embargo, para años posteriores al décimo, todos los modelos tienden a estabilizar el rendimiento. Por ejemplo, en la tabla 4 se observa un aumento con variaciones mínimas en el modelo Logistic después del duodécimo año, con un rendimiento que oscila entre 25,83 y 25,86 t de FFB, mientras que el rendimiento reportado por los productores tiende a disminuir progresivamente (figuras 1 y 2). Este efecto de reducción del rendimiento en edades avanzadas del cultivo no fue correctamente pronosticado por los modelos utilizados.

En Malasia se reportó el máximo potencial de producción registrado y pronosticado con modelos no lineales, que oscila entre 35 y 38 t/ha [10]. Estos son rendimientos representativos de la zona de estudio y varían significativamente respecto de los reportados en esta investigación, en la que se registró y pronosticó un rendimiento máximo que oscilaba en un rango de 23 a 26 t/ha, aproximadamente 32% menor.

Actualmente, en Costa Rica se reporta una productividad anual promedio de 14 a 17 t/ha [4], afectada por la enfermedad de la “flecha seca” y los bajos precios internacionales, que se puede traducir en una menor retribución económica para el pequeño productor y refleja un manejo deficiente del cultivo. Sin embargo, existen fincas donde se ha reportado una productividad de hasta 24 t de FFB/ha.

Cuadro 4. Simulación de rendimientos de palma aceitera (Elaeis guineensis) para los modelos no lineales con transformación Box-Cox.

Edad	Rendimiento (FFB/ha)	Modelo no lineal								Media	D.E.	C.V. (%)
		Chapman-Richard´s	Gompertz	Log-logistic	Logistic	Monomo-lecular	Morgan-Mercer-Flodin	Richard´s	Von Bertalanffy
3	9	8,41	8,11	7,79	8,24	8,04	8,69	8,77	6,99	8,13	0,57	6,97
4	13	13,45	13,93	14,60	13,60	14,28	12,92	13,28	16,53	14,08	1,13	8,03
5	16	18,25	18,83	19,42	18,65	18,95	18,72	17,62	21,77	19,03	1,23	6,45
6	18	21,66	22,04	22,16	22,12	21,93	22,56	25,56	23,98	22,75	1,34	5,89
7	20	25,73	23,88	23,66	24,05	23,69	24,36	25,56	24,83	24,47	0,82	3,36
8	22	25,73	24,87	24,50	25,02	24,69	25,15	25,56	25,15	25,08	0,42	1,66
9	23	25,73	25,38	25,01	25,47	25,24	25,51	25,56	25,27	25,40	0,23	0,89
10	23	25,73	25,63	25,32	25,69	25,54	25,68	25,56	25,31	25,56	0,16	0,64
11	24	25,73	25,76	25,52	25,78	25,71	25,77	25,56	25,33	25,65	0,16	0,63
12	24	25,73	25,83	25,65	25,83	25,80	25,82	25,56	25,33	25,69	0,17	0,68
13	24	25,73	25,86	25,74	25,84	25,85	25,85	25,56	25,34	25,72	0,19	0,72
14	24	25,73	25,87	25,81	25,85	25,87	25,87	25,56	25,34	25,74	0,19	0,75
15	23	25,73	25,88	25,85	25,86	25,89	25,88	25,56	25,34	25,75	0,20	0,78
16	23	25,73	25,89	25,89	25,86	25,89	25,88	25,56	25,34	25,76	0,21	0,80
17	23	25,73	25,89	25,92	25,86	25,90	25,89	25,56	25,34	25,76	0,21	0,81
18	23	25,73	25,89	25,94	25,86	25,90	25,89	25,56	25,34	25,76	0,21	0,82
19	22	25,73	25,89	25,95	25,86	25,90	25,89	25,56	25,34	25,77	0,21	0,83
20	22	25,73	25,89	25,96	25,86	25,90	25,89	25,56	25,34	25,77	0,22	0,84
21	22	25,73	25,89	25,97	25,86	25,90	25,89	25,56	25,34	25,77	0,22	0,84
22	21	25,73	25,89	25,98	25,86	25,90	25,89	25,56	25,34	25,77	0,22	0,85
23	21	25,73	25,89	25,99	25,86	25,90	25,90	25,56	25,34	25,77	0,22	0,85
24	21	25,73	25,89	25,99	25,86	25,90	25,90	25,56	25,34	25,77	0,22	0,85
25	21	25,73	25,89	26,00	25,86	25,90	25,90	25,56	25,34	25,77	0,22	0,86

Nota: D.E.= Desviación estándar; C.V.= Coeficiente de variación.

En todos los modelos no lineales utilizados inicialmente, la hipótesis de normalidad de los residuos fue rechazada debido a la posible presencia de sesgo en la respuesta de los agricultores. La ausencia de normalidad se logró corregir empleando la transformación Box-Cox, con un análisis previo para la selección del factor “lambda” [23]. No obstante, los parámetros resultantes luego del ajuste con Box-Cox no son comparables a los parámetros reportados en otras investigaciones [10]. Además, no se conoce ningún otro autor que haya aplicado la transformación Box-Cox en modelos de curvas de rendimiento de la palma aceitera, de la misma manera que se realizó en esta propuesta (cuadro 3).

Conclusiones

Todos los modelos no lineales utilizados generaron un patrón de pronóstico aceptable y se consideraron aptos para pronosticar el rendimiento anual de palma aceitera en la zona sur de Costa Rica, a pesar del extenso ciclo de vida característico de los cultivos perennes.

La transformación Box-Cox propició una mejora generalizada en los criterios estadísticos de eficiencia del pronóstico y se consideró idónea para reducir los problemas de normalidad en el pronóstico de los residuos. Después de aplicar la transformación Box-Cox, el modelo Morgan-Mercer-Flodin probó ser el de mayor eficiencia de pronóstico, seguido por los modelos Richard´s, Gompertz, Log-logistic y Logistic.

Sin embargo, con la intención de mejorar los ajustes del pronóstico en la modelación del rendimiento de la palma aceitera y otros cultivos perennes importantes para el sector agrícola de Costa Rica (el cultivo de café, por ejemplo), es importante obtener de los productores información más exacta para reducir el sesgo estadístico. La importancia de este factor se dedujo del hecho que los productores indicaran que las plantaciones de palma aceitera se renovaban periódicamente, pero realizado el estudio, se concluyó que las renovaciones podrían no ser las óptimas, debido a que todos los modelos no lineales tendieron a estabilizar la predicción del rendimiento en edades avanzadas de la plantación, mientras que el rendimiento reportado por los productores tendió a disminuir progresivamente.

Para futuras investigaciones se considera oportuno realizar un análisis costo-beneficio para determinar el momento óptimo para la renovación del cultivo de palma aceitera, con el fin de proveer de conocimientos al productor y al sector agrícola de Costa Rica.

Referencias

[1] T. Mielke, «Global price outlook of palm oil and other vegetable oils». ISTA Mielke GmbH, 2020 [En línea]. Disponible en: https://www.oilworld.biz/t/publications/monthly.

[2] A. González-Cárdenas, «La agroindustria de la palma de aceite en América», Rev. Palmas, vol. 37, n.o 2, pp. 215-228, 2016.

[3] INEC, «VI Censo Nacional Agropecuario. Resultados generales». INEC, 2015 [En línea]. Disponible en: INEC. http://www.inec.go.cr/censos/censo-agropecuario-2014.

[4] S. Mora e Y. Quirós, Boletín Estadístico Agropecuario N.°29: Serie Cronológica 2015-2018, SEPSA, San José, Costa Rica, 29, 2019 [En línea]. Disponible en: http://www.sepsa.go.cr/productos.html.

[5] M. Mosquera y E. García, «Impacto social de la agroindustria de palma de aceite», Rev. Palmas, vol. 26, n.o 2, pp. 11-19, 2005.

[6] B. Algieri, «Price volatility, speculation and excessive speculation in commodity markets: Sheep or shepherd behaviour?», Econstor, n.o 166, pp. 1-37, 2012.

[7] T. Correa, Palma aceitera: entre la «flecha seca» y la variación de precios internacionales. San José, Costa Rica: INFOCOOP, 2015.

[8] G. A. Torres et al., «Bur rot caused by Phytophthora palmivora: A destructive emerging disease of oil palm,» Phytopathology, n.o 106, pp. 320-329, 2016. doi: https://doi.org/10.1094/PHYTO-09-15-0243-RVW.

[9] CANAPALMA, «Precio de fruta de palma aceitera: fruta entregada», Boletín, diciembre 2019, 2019 [En línea]. Disponible en: http://www.canapalma.cr/.

[10] A. Khamis et al., «Nonlinear growth models for modeling oil palm yield growth,» Journal Math. Stat., vol. 85, pp. 84-90, 2005. doi: https://doi.org/10.3844/jmssp.2005.225.233.

[11] F. Köhn et al., «Modeling the growth of the Goettingen minipig,» J. Anim. Sci., vol. 85, pp. 84-90, 2007. doi: https://doi.org/10.2527/jas.2006-271.

[12] A. Sabbioni et al., «Effect of sex and season of birth on Gompertz growth curve parameters in “Nero di Parma” pigs,» J. Anim. Sci., vol. 8, n.o 4, pp. 719-729, 2009. doi: https://doi.org/10.4081/ijas.2009.719.

[13] J. A. Monte et al., «Growth analysis and yield of tomato crop under different irrigation depths,» Rev. Bras. Eng. Agríc. E. Ambient., vol. 17, n.o 9, pp. 926-93, 2013. doi: https://doi.org/10.1590/S1415-43662013000900003.

[14] Prajneshu and K. P. Chandran, «Computation of compound growth rates in agriculture: Revisited,» Agric. Econ. Res. Rev., vol. 18, pp. 317-324, 2005. doi: https://doi.org/10.22004/ag.econ.58480.

[15] A. Rajarathinam and B. Vinoth, «Statistical modeling for wheat (Triticum aestivum) crop production,» Int. J. Stat. Appl., vol. 2, n.o 4, pp. 40-46, 2012. doi: https://doi.org/10.5923/j.statistics.20120204.03.

[16] S. Panwar et al., «Forecasting of growth rates of wheat yield of Uttar Pradesh through non-linear growth models,» Indian J. Agrocultural Sci., vol. 84, n.o 7, pp. 856-859, 2014.

[17] S. Pal and D. Mazumdar, «Forecasting groundnut production of India using nonlinear growth models,» J. Crop Weed, vol. 11, n.o Special Issue, pp. 67-70, 2015.

[18] R. H. V. Corley, J. J. Hardon, and G. Y. Tan, «Analysis of growth of the oil palm (Elaeis guineensis Jacq.) I. Estimation of growth parameters and application in breending,» Euphytica, vol. 20, pp. 307-315, 1971. doi: https://doi.org/10.1007/BF00056093.

[19] L. S. Woittiez et al., «Yield gaps in oil palm: A quantitative review of contributing factors,» Eur. J. Agron., vol. 83, pp. 57-77, 2017. doi: https://doi.org/10.1016/j.eja.2016.11.002.

[20] L. von Bertalanffy, «A quantitative theory of organic growth (Inquiries on growth laws, II),» Hum. Biol., vol. 10, n.o 2, pp. 181-213, 1938.

[21] R. Juárez-Romero y R. Searcy-Bernal, «Von Bertalanffy growth model for the pismo clam (Tivela stultorum), based on age-length data from commercial catches,» Sci. Mar., vol. 20, n.o 1, pp. 81-92, 1994. doi: https://doi.org/10.7773/cm.v20i1.952.

[22] M. M. Tariq et al., «Comparisson of non-linear functions to describe the growth in mengali sheep breed of Balochistan,» Pak. J. Zool., vol. 45, n.o 3, pp. 661-665, 2013.

[23] G. E. Box and D. R. Cox, «An analysis of transformations,» J. R. Stat. Soc., vol. 26, n.o 2, pp. 211-252, 1964.

---