Secuenciación de operaciones por simulación en la empresa Puntadas, S.G.

Sequencing of operations by simulation in the company Puntadas, S.G.

Erik Orozco-Crespo1, Neyfe Sablón-Cossío2,
Yadamy Rodríguez-Sánchez3, Jenifer Cristina González-Garzón4,
Fabiola Sánchez-Galván5

Fecha de recepción: 12 de noviembre de 2019
Fecha de aprobación: 27 de febrero de 2020

Orozco-Crespo, E; Sablón-Cossío, N;
Rodríguez-Sánchez, Y; Cristina González-Garzón, J;
Sánchez-Galván, F. Secuenciación de operaciones por simulación en la empresa Puntadas, S.G. Tecnología en Marcha. Vol. 34-1. Enero-Marzo 2021. Pág 55-68.

https://doi.org/10.18845/tm.v34i1.4823

Palabras claves

Secuenciación; simulación; reglas de prioridad; programación de las operaciones.

Resumen

La secuenciación de los pedidos de los clientes es un reto para la programación de las operaciones en una empresa. Este se complejiza todavía aún más si se trata de una empresa del sector textil, debido a que responde a pedidos cada vez más personalizados. El orden que se les dé a estos pedidos repercute significativamente en el desempeño de las operaciones. En este contexto se diseñó un modelo de simulación en FlexSim para medir el impacto de la aplicación de diferentes reglas de prioridad para la secuenciación de los pedidos de los clientes en el caso de las operaciones de la empresa “Puntadas, S.G.”. Los resultados fueron presentados al secuenciar los pedidos correspondientes a cuatro semanas del Programa Maestro de Producción (MPS) en el modelo de simulación. Con esto se determinó que la regla de prioridad Shortest Processing Time (SPT) sería la que mejor impactaría el desempeño general de las operaciones, sobre todo mediante un aumento en la fiabilidad de un 4.49%, respecto a la regla First-Come First-Served (FCFS) que es la implementada en la actualidad.

Abstract

The sequencing of customer orders is a challenge for scheduling operations in a company. This becomes even more complex if it is a company in the textile sector, since it responds to increasingly personalized orders. The order given to these orders has a significant impact on the performance of operations. In this context, a simulation model was designed in FlexSim to measure the impact of the application of different priority rules for the sequencing of customer orders in the case of the operations of the company “Puntadas, S.G.”. The results were presented by sequencing the orders corresponding to four weeks of the Master Production Program (MPS) in the simulation model. With this, it was determined that the Shortest Processing Time (SPT) priority rule would be the one that would best impact the general performance of operations, especially through an increase in reliability of 4.49%, compared to the First-Come First-Served rule. (FCFS) which is currently implemented.

Keywords

Sequencing; simulation; priority rules; operation scheduling.

Introducción

El sistema de producción en una industria es parte del éxito o fracaso de ella [1], y cuenta con variables de entrada, de proceso y de salida, alineadas con la estrategia global empresarial [2]. Este se enfoca en las necesidades de los clientes y en los pedidos para la programación de la producción a corto, mediano y largo plazo [3].

La complejidad de los sistemas de producción se ha venido acrecentando en la medida en que el mercado se ha vuelto más exigente, como consecuencia de la evolución de la fabricación en masa a la fabricación de productos más individualizados [4]. Los mercados actuales definen los requerimientos de la industria; estos requerimientos reflejan un alto sentido de personalización, puesto que, en la última década, el rápido cambio de los productos se está convirtiendo en un estilo de vida. Los clientes esperan mejor calidad, mayor variedad y mejor rendimiento de los productos [5]. En estas circunstancias, aspectos como la flexibilidad, la adaptabilidad y la rapidez de respuesta han pasado de ser deseables a convertirse en la clave del éxito en muchas empresas [6] y en elementos que considerar en la planificación de la producción. La metodología que se asuma para alcanzar tales fines debe conducir a la obtención de resultados útiles [7].

La secuenciación de operaciones forma parte del nivel de planificación a corto plazo [3, 8]. Es una rama de la optimización matemática que ha desarrollado su propia metodología utilizando herramientas matemáticas y computacionales variadas [9]. Su objetivo es la asignación de tareas con un conjunto limitado de recursos disponibles en un intervalo fijado, en las que se aplican determinados criterios para su optimización [10].

En las últimas décadas, debido a los avances en el área de la informática, las nuevas formas de producción (tecnología 3D) y la elaboración de materiales alternativos, la toma de decisiones en el diseño de productos y procesos ha avanzado notablemente [11]. En este sentido, la simulación de estos sistemas a partir del desarrollo de lenguajes de programación y software comerciales constituye una de las técnicas más empleadas en la Investigación de Operaciones y Ciencias de la Administración [12].

Para una correcta secuenciación, el criterio de determinación de las reglas de prioridad es de fundamental relevancia a la hora de minimizar costos y tiempos de procesamiento. La simulación constituye una herramienta importante que se puede utilizar para cotejar distintas reglas de secuenciación [13]. Además, permite el estudio de sistemas donde intervienen una gran cantidad de variables (muchas de índole aleatorio), sin la necesidad de modificar el proceso real, logrando obtener un mejor entendimiento de su comportamiento y poder experimentar en la búsqueda de mejoras y soluciones a la problemática que se defina [14]. Con este entorno se relaciona el planteamiento del estudio de caso que aquí se trata, caso perteneciente al sector textil de la provincia Imbabura en el Ecuador.

La fábrica Puntadas, S.G., ubicada en Imbabura, Ecuador, se dedica a la producción de ocho tipos de camisetas en un proceso productivo job-shop que funciona bajo pedidos, es decir, en un sistema make to order. Dichas características lo hacen un proceso productivo difícil de planificar en el corto plazo.

Los pedidos de los clientes son receptados por el Gerente y se les establece una fecha de entrega que es convenida entre las partes. El Gerente define la fecha de entrega sobre la base de su experiencia. La secuenciación de estos pedidos se realiza mediante la regla de prioridad first-come, first-served (FCFS), considerando la fecha de recepción del pedido, es decir que se comienza a trabajar en los pedidos en el mismo orden en el que son receptados por el Gerente.

Durante el desarrollo del trabajo se manifestó que existen incumplimientos en la fecha de entrega de los pedidos a los clientes, lo que se traduce en afectación de la fiabilidad de las operaciones. A lo anterior se añade que no se han desarrollado investigaciones que permitan detectar si otras reglas de prioridad pudieran mejorar el desempeño de las operaciones en el corto plazo.

Ante tal situación, el objetivo principal del trabajo que aquí se resume se determinó como el de diseñar un modelo de simulación en FlexSim para medir el desempeño de las operaciones en la empresa “Puntadas S.G.”, secuenciando la producción por medio de diferentes reglas de prioridad.

Aplicaciones de la simulación a los problemas de secuenciación de la producción

La simulación permite a los gerentes evaluar el desempeño de todos los aspectos relacionados con los procesos y las operaciones, considerando todos los parámetros que puedan afectar su desempeño [15, 16]. Disímiles autores han contextualizado su empleo a los problemas de secuenciación de pedidos. Ejemplo de ello son sus aplicaciones:

•En el impacto que tendría en el rendimiento del sistema el empleo de las diferentes reglas de prioridad para definir la secuencia en cada una de las estaciones de trabajo [17, 18].

•En la elaboración de órdenes de trabajo en el menor tiempo posible, en una empresa con un ambiente de producción tipo taller [19].

•En la didáctica como soporte al aprendizaje de la secuenciación de trabajos en una configuración de producción del tipo job-shop [20].

•En el estudio reportado por Ang y autores [13], se experimentó mediante simulación con varias reglas de secuenciación en una empresa real cuyo sistema de producción corresponde a un job-shop. Entre las reglas aplicadas, ellos mencionan shortest setup time (SST), shortest processing time (SPT), shortest processing and setup time (SPST), earliest due date (EDD), least process (LP) y lowest volume (LV). Midieron el desempeño con cada regla de acuerdo con el inventario en proceso y el tiempo total de elaboración.

•En la comparación y validación de 30 reglas de secuenciación en un job-shop, midiendo el desempeño bajo diferentes funciones objetivo. Entre las reglas aplicadas están first-input first-output (FIFO), last-input first-output (LIFO), long process time (LPT), shortest processing time (SPT) y como funciones objetivo, miden el tiempo medio de flujo, el retraso promedio y el máximo retraso [21].

•En la modelación de redes para minimizar el makespan al programar un job-shop, evaluando el desempeño por comparación entre diferentes reglas de secuenciación: FIFO, LIFO, highest value first (HVF), lowest value first (LVF) [22].

Metodología

Para la realización del estudio de simulación es necesario definir una metodología lógica y sistémica que garantice que el modelo funcione, lo cual se hizo con base en el estudio descrito por Hermoso-Ayala [29]. La figura 1 muestra la naturaleza iterativa del proceso para realizar un trabajo de simulación.

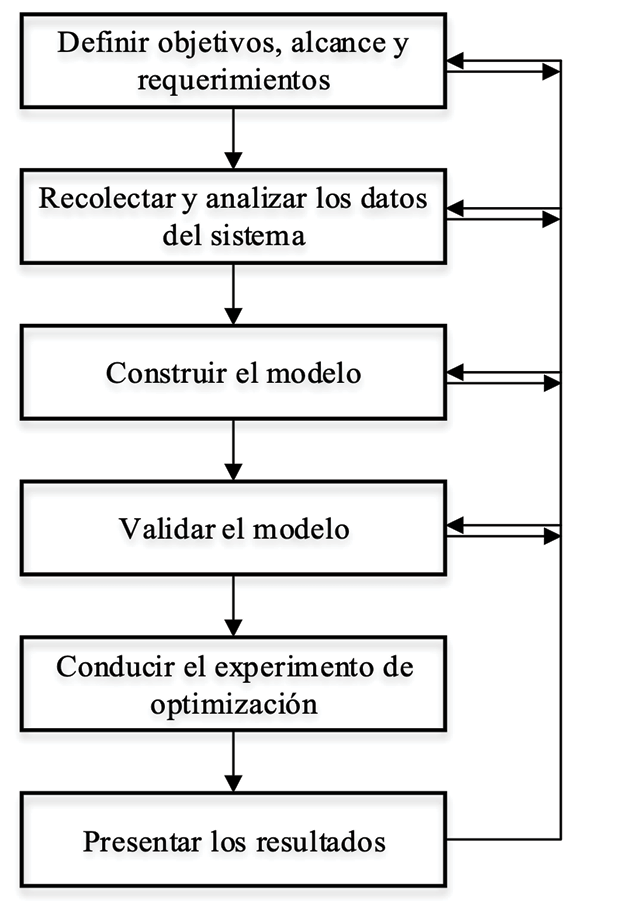
Figura 1. Proceso iterativo de la simulación. Fuente: [23].

Definir objetivos, alcance y requerimientos

En estrecha relación con el planteamiento de los objetivos, es necesario identificar con claridad el sistema que modelar, es decir, contar con la información suficiente para establecer el modelo conceptual para el caso de estudio [24, 25]. Los objetivos deben ser planteados de forma tal que guarden especial relación con las variables de respuesta y de decisión del modelo. Las primeras se definen a partir de un análisis de sensibilidad; mientras que las segundas, por medio de un análisis de la mejor configuración para alcanzar los objetivos de rendimiento deseados en la optimización [23].

Recolectar y analizar los datos del sistema

En este paso se procede a dividir los datos en tres categorías: estructurales, operacionales y numéricos. En la primera se consideran la cantidad de locación de recursos, así como las redes de abastecimiento a los puestos de trabajo. El análisis de los datos operacionales permite explicar cómo opera el sistema, es decir, cuándo, dónde y cómo se realizan las actividades [26].

Los datos numéricos representan la información útil para la determinación de las distribuciones de probabilidad asociadas a cada una de las variables aleatorias necesarias para la simulación [27], lo que significa que, si no se cuenta con la información requerida o se desconfía de ella, es necesario realizar un estudio estadístico del comportamiento de dichas variables, para luego proceder a incluirlas en el modelo [25].

Construir el modelo

La construcción del modelo consiste en realizar una representación simplificada de la realidad. Es importante tomar en cuenta que una actividad debe considerarse siempre en términos de su efecto sobre otros elementos del sistema, en lugar de la forma detallada en la que se lleva a cabo [28]. Tales mecanismos detallados son intrascendentes para las entidades globales del flujo y utilización de los recursos.

El modelo se construye con base en elementos estructurales, tales como máquinas, personas, elementos de trabajo y áreas de trabajo, ya antes definidos. Es necesario precisar el comportamiento de los diferentes elementos físicos en el sistema y cómo interactúan. Estos incluyen hojas de ruta, operaciones, las llegadas, el movimiento de recursos, reglas de selección de tareas, horarios de recursos y los tiempos de parada y reparaciones [23].

Validar el modelo

El proceso de validación se garantiza, principalmente, desde la misma programación de los modelos [29, 30]. Posteriormente, es necesaria la realización de una serie de pruebas simultáneas con información de entrada real para observar su comportamiento y analizar sus resultados. El propósito en este paso corresponde a obtener un comportamiento similar al que se presenta en el proceso real si es que este existe; de no ser el caso, la validación consiste en introducir algunos escenarios sugeridos por el cliente y demostrar su congruencia [25, 31].

Conducir el experimento de optimización

Este paso comienza realizando un análisis de sensibilidad como parte del estudio de optimización, lo cual implica la realización de corridas o réplicas experimentales que permitan hacer comparaciones con el comportamiento histórico del sistema [23, 32]. A partir de estas corridas pilotos, se detectan los momentos en que las variables de respuesta alcanzan la estabilidad y se determina la cantidad definitiva de réplicas que ejecutar, asumiendo un nivel de confianza y los niveles de exactitud arrojados por las desviaciones típicas determinadas en las variables de respuesta. Dunna y autores [25] hacen énfasis en generar escenarios pesimistas, intermedios y optimistas, que permitan determinar la influencia de variables independientes en las principales variables de respuesta consideradas (variables dependientes).

Resultados y discusión

Definir objetivos, alcance y requerimientos

El alcance del modelo de simulación comprendió el proceso de producción de camisetas en su totalidad. Se consideraron 8 tipos de camisetas como los más representativos en cantidad y frecuencia de producción. Además, se programó la producción de las cuatro semanas pertenecientes al mes de noviembre de 2019, por ser un mes pico en demanda; el Plan Maestro de Producción (MPS) de ese mes se muestra en el cuadro 1.

Cuadro 1. Plan maestro de producción (MPS).

Semana 1						Semana 2						Semana 3						Semana 4
L	K	M	J	V		L	K	M	J	V		L	K	M	J	V		L	K	M	J	V
		50			50			175			175		85				85				127
		50			50						0	280	86				366			113
			135		135	40					40						0	61				300
			175		175					85	85						0	61
				125	125			45			45						0		225			114
		90			90				75		75				80		80					85
					0				65		65				98		98				67
70					70			55			55					112	112				63

La empresa procesa los pedidos de los clientes bajo la regla FCFS y posee como uno de sus objetivos estratégicos el de “cumplir los pedidos de los clientes dentro del plazo convenido con ellos”. De lo anterior se dedujo que la fiabilidad de la respuesta constituye una de sus principales prioridades.

El objetivo general de la simulación fue el de crear un modelo en FlexSim que permitiera medir el desempeño del sistema productivo de la Empresa Puntadas S.G., secuenciando la producción por medio de diferentes reglas de prioridad.

Objetivos específicos de la simulación:

1.Medir el desempeño actual del sistema productivo de la Empresa, secuenciando la producción mediante la regla de prioridad FCFS.

2.Medir el impacto de otras reglas de prioridad en las variables de respuesta del modelo.

3.Analizar cuál regla de prioridad es la que mejor se ajusta a los objetivos estratégicos de la empresa, en específico en el área de operaciones.

Se definió como variable independiente del modelo la asociada a las reglas de prioridad. Se consideraron las reglas siguientes: FCFS, con código 1; EDD, con código 2; SPT, con código 3, y la regla critical ratio (CR), con código 8.

Se definieron como variables de respuesta o dependientes las que se detallan en el cuadro 2.

Cuadro 2. Variables de respuesta.

Objetivos específicos de la simulación	Variable dependiente	Denominación	UM
Determinar el tiempo promedio de flujo de los pedidos según la regla de prioridad k	Media del tiempo promedio de flujo	TPFk	min.
Determinar el tiempo promedio de adelanto de los pedidos según la regla de prioridad k	Media del tiempo promedio de adelanto	TPAk	min.
Determinar el tiempo promedio de retraso de los pedidos según la regla de prioridad k	Media del tiempo promedio de retraso	TPRk	min.
Determinar el promedio de la producción en proceso según la regla de prioridad k	Media de la producción en proceso	WIPk	pedido
Determinar la productividad del proceso según la regla de prioridad k	Media de la productividad del proceso de producción	Ptk	u./min.
Determinar la fiabilidad del proceso según la regla de prioridad k	Media de la fiabilidad del proceso de producción, calculada como el porcentaje de los pedidos cumplidos dentro del plazo de entrega pactado con los clientes	Fk	%

Recolectar y analizar los datos del sistema

La recolección de los datos se dividió en dos categorías: estructurales y numéricos. Los primeros se definieron como los elementos del sistema: máquinas, producción en proceso, los trabajadores y la distribución en planta de la fábrica. Los segundos se obtuvieron de la toma de datos y el análisis estadístico mediante el empleo de la herramienta Expertfit (Módulo de ajuste de curvas de FlexSim). Dichos datos numéricos se centraron en los tiempos de las operaciones relacionadas para cada uno de los tipos de camisetas y todos se ajustaron a la distribución normal.

Construir el modelo

Para la construcción del modelo se añadieron un source, processors, queues, separator, racks, task executers y dispatchers6, que resultaron en la vista superior del modelo que se muestra en la figura 2.

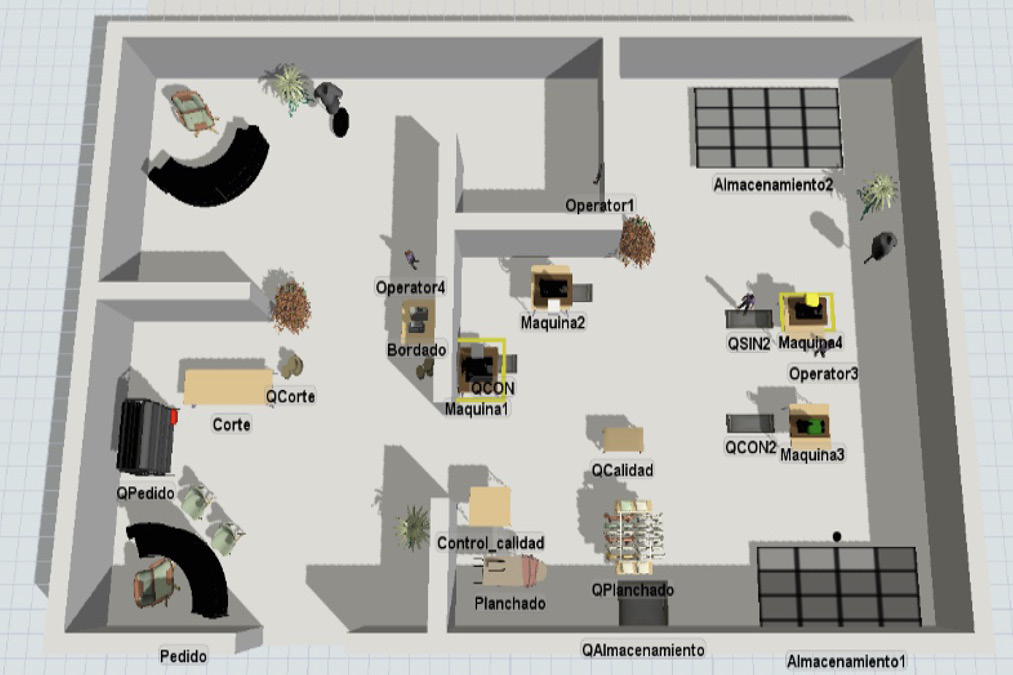
Figura 2. Vista superior del modelo de simulación.

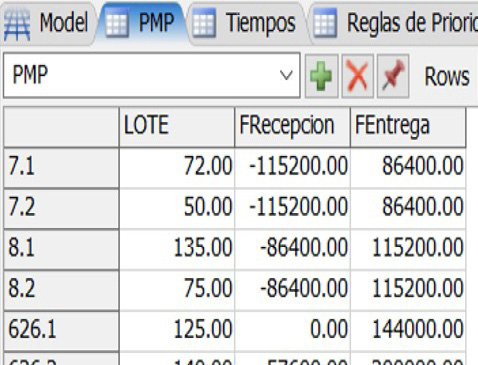
Se añadieron cuatro Global Tables y cinco Global Lists (ver figura 3).

a) PMP	b) Tiempo total en el sistema
c) Tiempos
d) Reglas de prioridad
e) Global lists
Figura 3. Global Tables7

1.PMP: Se indicó el tamaño de los pedidos (unidades) y sus correspondientes fechas de recepción y de entrega (segundos). Esta tabla se derivó del MPS de la empresa.

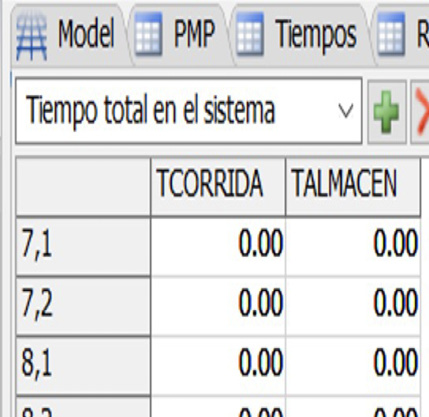
2.Tiempo total en el sistema: Se indicaron los tiempos de corridas simulados para cada ítem y los tiempos de permanencia de los pedidos en almacén hasta la fecha de entrega.

3.Tiempos (segundos): Se describieron los tiempos de ciclo de cada ítem en las diferentes operaciones del proceso; los tiempos de corrida de los pedidos, determinados al multiplicar el tamaño del pedido por el tiempo de ciclo; el tiempo total de procesamiento de cada pedido al pasar por todas las operaciones, y las operaciones restantes al inicio del proceso de producción de los pedidos.

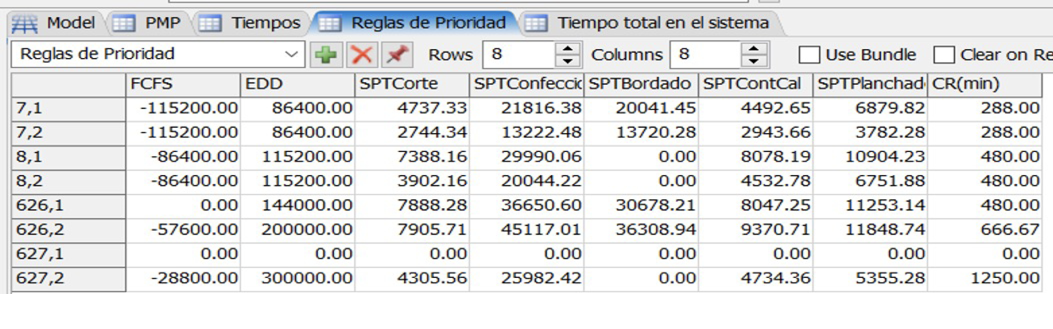
4.Reglas de prioridad: Las reglas de prioridad consideradas fueron: FCFS, EDD, SPT y CR.

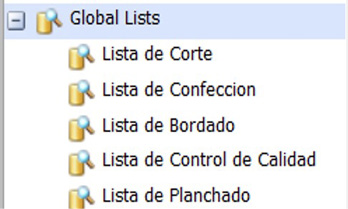
5.Global lists: Las cinco Global Lists se correspondieron con cada una de las operaciones del proceso productivo. Estas guiaron la secuenciación entre el almacenamiento previo y la producción, o indicaron la secuenciación entre las operaciones (en los Queues) y la operación en sí (Processor o Separator).

Se programaron funcionalidades del modelo, específicamente en el Open Model y en el Reset Model, las cuales fueron las responsables de reescribir los valores aleatorios del tiempo de las operaciones en la Global Table “Tiempos”, a partir de lo cual se derivaron el resto de los cálculos en las Global Tables restantes.

Se colocaron dos labels en el source del modelo: una para contar la cantidad de pedidos de la semana y la otra para contar cuántos de estos pedidos se entregan atrasados respecto a la fecha programada. Ambas labels fueron necesarias para el cálculo de la fiabilidad.

Una Global Variable “Regla” definió la regla de prioridad con la que se corrió el modelo. Las variables de respuesta de la tabla 2 fueron programadas en el Performance Measures del Experimenter.

Validar el modelo

El proceso de validación se garantizó, primeramente, a partir de la propia programación del modelo. En tal sentido, se emplearon algunas declaraciones propias de FlexSim, que unidas a informaciones de entrada real, permitieron observar el comportamiento de las variables respuesta y que este fuera congruente con el desempeño real del sistema.

Se creó un dashboard para la inclusión de los operarios y para el cálculo de la productividad del sistema, en aras de visualizar si el comportamiento del modelo se asemejaba a la realidad del proceso (ver figura 4).

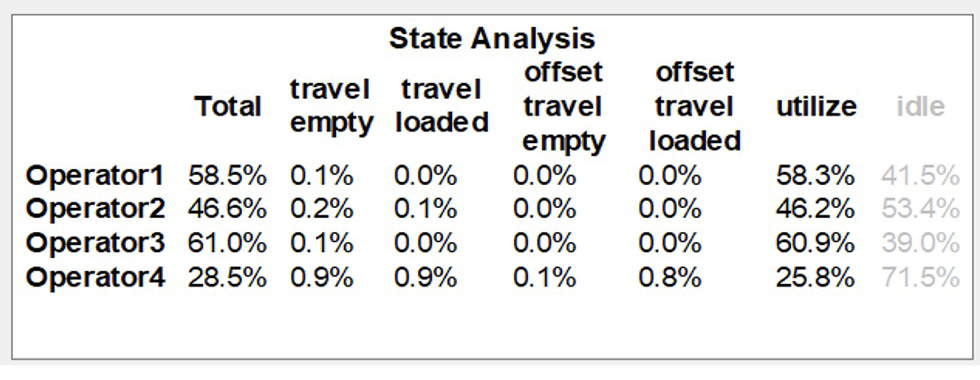
Figura 4. Dashboard para el análisis de la ártición de cada utilización de los operario.

Se corrieron cincuenta réplicas iniciales para determinar la cantidad de réplicas necesarias que permitieran validar el modelo y estimar las variables de respuesta (ver cuadro 3). Así se demostró que las cincuenta réplicas desarrolladas fueron suficientes para validar el modelo y para estimar las variables de respuesta.

Cuadro 3. Cálculo de la cantidad de réplicas necesarias.

Variable	UM		S	LI	LS	IC	e	Condición IC≤2*e	n
TPF	min.	1997,00	60,00	1980,00	2014,00	34,00	20	Si	36,36
TPA	min.	264,00	13,50	260,10	267,80	7,70	20	Si	1,84
TPR	min.	684,00	53,00	668,00	699,00	31,00	20	Si	28,37
WIP	pedido	1,82	0,05	1,81	1,83	0,03	0,25	Si	0,16
Pt	u./min.)	0,22	0,01	0,22	0,22	0,00	0,01	Si	2,46
: media. S: desviación estándar. LI: Límite inferior. LS: Límite superior. IC: Amplitud del intervalo de confianza (). e: error que se está dispuesto a asumir en la estimación. n: cantidad de réplicas calculadas a partir de la expresión

Además, se comparó la productividad real del proceso con la productividad arrojada por el modelo. Para ello se tomaron veinte datos históricos de productividad semanal (aproximadamente 5 meses) y se compararon con una corrida del modelo (50 réplicas) bajo la regla de prioridad FCFS (ver cuadro 4).

Cuadro 4. Productividad para 20 semanas.

Semana	Producción (u./sem.)	FPD (min./sem.)	Productividad (u./min.)
1	513	2340	0,2192
2	509	2319	0,2194
3	487	2209	0,2204
4	428	1915	0,2235
5	539	2470	0,2182
6	482	2185	0,2206
7	484	2193	0,2205
8	508	2314	0,2194
9	548	2517	0,2179
10	580	2673	0,2168
11	518	2364	0,2190
12	548	2516	0,2179
13	548	2513	0,2179
14	537	2460	0,2183
15	507	2308	0,2195
16	554	2545	0,2177
17	514	2343	0,2192
18	578	2665	0,2169
19	538	2465	0,2183
20	512	2335	0,2193

Dicha comparación se realizó en el Statistical Package for the Social Sciences (SPSS) por medio de la prueba T para muestras independientes, probando como hipótesis nula que las productividades observadas en el proceso eran iguales a las productividades obtenidas con el modelo de simulación (ver figura 5).

Figura 5. Salida del SPSS para la prueba T, para muestras independientes.

A partir de esta prueba se dedujo que no existía evidencia suficiente como para rechazar la hipótesis nula, a un 5% de nivel de significación, por lo que pudo afirmarse que el modelo de simulación tuvo un comportamiento similar al proceso de producción real, quedando así validado el modelo.

Presentación de los resultados

Posteriormente a la corrida del modelo para las cuatro semanas y bajo las reglas de prioridad analizadas, se obtuvieron los resultados para las variables de respuesta, que se resumen en el cuadro 5.

Cuadro 5. Resultados del modelo para las cuatro semanas en estudio.

Semana 1
	TPF (min)	TPA (min)	TPR (min)	WIP(pedido)	Pt (u/min)	F(%)
FCFS	19973	2641	6843	1,8193	0,21981	42,001
EDD	17901	1613	3741	1,2442	0,21912	27,163
SPT	18472	1742	4442	1,2271	0,21853	30,502
CR	17901	1613	3741	1,2442	0,21912	27,163
Semana 2
	TPF (min)	TPA (min)	TPR (min)	WIP(pedido)	Pt (u/min)	F(%)
FCFS	23663	584	6842	1,8004	0,22251	26,703
EDD	21931	1501	6031	1,5513	0,20053	33,401
SPT	23172	1303	7073	1,5162	0,20172	25,304
CR	25464	1382	9444	1,1491	0,15944	26,902
Semana 3
	TPF (min)	TPA (min)	TPR (min)	WIP(pedido)	Pt (u/min)	F(%)
FCFS	33023	4231	12563	1,4143	0,17751	28,003
EDD	27461	1493	4271	0,8832	0,17222	35,302
SPT	27642	1542	4492	0,8721	0,17103	41,201
CR	27461	1493	4271	0,8832	0,17222	35,302
Semana 4
	TPF (min)	TPA (min)	TPR (min)	WIP(pedido)	Pt (u/min)	F (%)
FCFS	24492	2143	6242	2,2812	0,20911	25,963
EDD	24593	2143	6333	2,3103	0,20902	25,963
SPT	21461	3221	4281	1,8101	0,20524	43,601
CR	24684	2472	6754	2,3454	0,20773	36,762
a: Los superíndices en cada valor indican el orden de los resultados de mejor (valor 1) a peor (valor 4).

A partir de estos resultados se pudo observar que las reglas de prioridad arrojaron desempeños diferentes según la estructura, la cantidad de los pedidos y las fechas de recepción y de entrega. En el cuadro 6 se promediaron los superíndices para las cuatro semanas, el total indicó que la regla SPT fue la que mejor desempeño proporcionó de forma general, por lo que en el orden quedó en el primer lugar con el menor de todos los promedios (valor de 2,00).

Cuadro 6. Promedio de los superíndices.

	TPF	TPA	TPR	WIP	Pt	F	Total
FCFS	2,75	2,25	2,50	2,50	1,00	2,50	2,33
EDD	1,50	2,50	1,50	1,50	2,25	2,25	2,08
SPT	1,75	2,00	2,00	2,00	3,00	2,00	2,00
CR	2,50	2,50	2,50	2,50	2,75	2,25	2,46

La regla de prioridad SPT permitió que el modelo obtuviera un incremento de la fiabilidad en un 4,49% respecto a la regla FCFS (ver cuadro 7), lo que implicaría una mejora en el cumplimiento de los pedidos dentro del plazo convenido con los clientes.

Cuadro 7. Resumen para las cuatro semanas en estudio.

	Pt (u./min.)	Variación (u./min.)	Variación ($/sem.)	F(%)	Variación (%)
FCFS	0,2072	-	-	30,67	-
EDD	0,2002	-0,0070	-82,28	30,46	-0,21
SPT	0,1991	-0,0081	-19,50	35,15	4,49
CR	0,1896	-0,0176	-42,30	31,53	0,87

No obstante, aplicando esta regla el modelo obtuvo una disminución de la productividad con una implicación de pérdida de 19,50 dólares a la semana.

Implementarla no es más que ordenar los pedidos de modo acorde al grado de complejidad tecnológica de su elaboración, dándoles prioridad a aquellos que consumen menor tiempo de procesamiento en cada una de las operaciones.

Conclusiones

El modelo de simulación desarrollado permite medir el desempeño del proceso de producción al aplicar diferentes reglas de prioridad. En el caso estudiado, ratificó la baja fiabilidad del sistema, con un promedio de 30,67%, lo cual apuntó a la necesidad de analizar los plazos de entrega que se habían venido pactando con los clientes y que no estaban ajustados a las condiciones reales del proceso de producción. Además, identificó la regla de prioridad SPT como aquella que mejor impactaría sobre el desempeño general de las operaciones. Este resultado coincide con la literatura, que considera la regla SPT como el concepto más importante en el ámbito de la secuenciación [3, 8]. De decidirse cambiar la secuenciación de los pedidos, de la regla de prioridad FCFS a la regla SPT, la fiabilidad del sistema podría mejorar en un 4,49%, consiguiéndose con la mejora uno de los objetivos estratégicos de la empresa.

Referencias

[1] F. Gu, J. Guo, P. Hall, and X. Gu, “An integrated architecture for implementing extended producer responsibility in the context of Industry 4.0,” (in English), International Journal of Production Research, vol. 57, no. 5, pp. 14 58-1477, 2019, doi: 10.1080/00207543.2018.1489161.

[2] A. de la Calle Vicente, A. Barinaga Naves, and J. C. Gietz Jiménez, “La colaboración como estrategia en la cadena de suministro: una visión metodológica,” Dyna Management, vol. 4, no. 1, 2016, doi: 10.6036/MN7809  

[3] L. J. Krajewski, M. K. Malhotra, and L. P. Ritzman, Operations Management Processes and Supply Chains. Boston: Pearson Education, 2019.

[4] S. Mittal, M. A. Khan, D. Romero, and T. Wuest, “A critical review of smart manufacturing & Industry 4.0 maturity models: Implications for small and medium-sized enterprises (SMEs),” (in English), Journal of Manufacturing Systems, Review vol. 49, pp. 194-214, 2018, doi: 10.1016/j.jmsy.2018.10.005.

[5] D. A. Burbano, J. D. López, and O. A. Rojas, “Definición de un método para la programación de la producción desde el paradigma de los sistemas holónicos de manufactura”, Ingeniería y Competitividad, vol. 17, no. 2, pp. 29-40, 2015.

[6] J. A. A. Araúzo, J. J. de Benito Martín, R. del Olmo Martínez, and P. A. S. Angulo, “Situación actual y expectativas de los sistemas de fabricación basados en agentes”, in VIII Congreso de Ingeniería de Organización, Leganés, 2004, pp. 1043-1052.

[7] J. D. Romero-Rojas, V. K. Ortiz-Triana, and Á. J. Caicedo-Rolón, “La teoría de restricciones y la optimización como herramientas gerenciales para la programación de la producción. Una Aplicación en la Industria de Muebles”, Revista de Métodos Cuantitativos para la Economía y la Empresa, vol. 27, pp. 74-90, 2019.

[8] R. B. Chase and F. R. Jacobs, Administración de operaciones: producción y cadena de suministros. México: McGraw-Hill, 2014.

[9] A. A. Correa Espinal, E. Rodríguez Velásquez, and M. I. Londoño Restrepo, “Secuenciación de operaciones para configuraciones de planta tipo flexible Job Shop. Estado del arte”, Avances en Sistemas e Informática, vol. 5, no. 3, pp. 151-161, 2008.

[10] R. Najarro, R. López, R. E. Racines, and A. Puris, “An Hybrid Genetic Algorithm to Optimization of Flow Shop Scheduling Problems under Real Environments Constraints,” Enfoque UTE, vol. 8, no. 5, pp. 14 - 25, 12/18 2017, doi: 10.29019/enfoqueute.v8n5.176.

[11] L. S. Dalenogare, G. B. Benitez, N. F. Ayala, and A. G. Frank, “The expected contribution of Industry 4.0 technologies for industrial performance,” (in English), International Journal of Production Economics, vol. 204, pp. 383-394, 2018, doi: 10.1016/j.ijpe.2018.08.019.

[12] E. Orozco-Crespo, N. Sablón-Cossio, and R. V. Saraguro-Piarpuezán, “Discrete event simulation for resource programming: Case of Ecuadorian textile industry,” in 2nd European International Conference on Industrial Engineering and Operations Management.IEOM 2018, 2018, vol. 2018: IEOM Society, JUL ed., pp. 1430-1443. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85066935485&partnerID=40&md5=03b0f0748f21d8fca61fb168732a596d

[13] L. Ang, K. Y. Wong, and W. P. Wong, “Simulation of sequencing rules in a five-similar-machine job shop,” in 16th International Business Information Management Association Conference, IBIMA 2011, vol. 1, Kuala Lumpur, 2011, International Business Information Management Association, IBIMA, pp. 61-67. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-84905123281&partnerID=40&md5=75c647382c1068b21538abd651438514

[14] J. Cano, E. Campo, and R. Gómez, “Simulación de eventos discretos en la planificación de producción para sistemas de confección modular”, Revista Técnica de la Facultad de Ingeniería Universidad del Zulia, vol. 41, no. 1, pp. 50-58, 01/01 2018.

[15] A. Moeuf, R. Pellerin, S. Lamouri, S. Tamayo-Giraldo, and R. Barbaray, “The industrial management of SMEs in the era of Industry 4.0,” (in English), International Journal of Production Research, vol. 56, no. 3, pp. 1118-1136, 2018, doi: 10.1080/00207543.2017.1372647.

[16] A. G. Frank, L. S. Dalenogare, and N. F. Ayala, “Industry 4.0 technologies: Implementation patterns in manufacturing companies,” (in English), International Journal of Production Economics, vol. 210, pp. 15-26, 2019, doi: 10.1016/j.ijpe.2019.01.004.

[17] N. Wang and O. Ghrayeb, “Dispatching Rules Application for a Parallel Machine Scheduling Problem Using Simulation,” in IIE Annual Conference. Proceedings, 2009, Institute of Industrial and Systems Engineers (IISE), p. 2085.

[18] N. Suresh Kumar and R. Sridharan, “Simulation-based metamodels for the analysis of scheduling decisions in a flexible manufacturing system operating in a tool-sharing environment,” The International Journal of Advanced Manufacturing Technology, vol. 51, no. 1, pp. 341-355, 2010/11/01 2010, doi: 10.1007/s00170-010-2603-9.

[19] M. Padilla, J. Guo, and R. Moraga, “An industrial application of simulation-based multi-objective scheduling,” in IIE Annual Conference and Expo 2013, San Juan, Institute of Industrial Engineers, pp. 2457-2464. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-84900320707&partnerID=40&md5=f83bafa7d872e94ce10e9b4a987f9c94

[20] J. A. Giraldo, C. A. Toro, and F. A. Jaramillo, “Learning about sequencing of jobs in a job shop simulation using,” (in Spanish), Formacion Universitaria, vol. 6, no. 4, pp. 27-38, 2013, doi: 10.4067/S0718-50062013000400004.

[21] V. Sels, N. Gheysen, and M. Vanhoucke, “A comparison of priority rules for the job shop scheduling problem under different flow time- and tardiness-related objective functions,” (in English), International Journal of Production Research, vol. 50, no. 15, pp. 4255-4270, 2012, doi: 10.1080/00207543.2011.611539.

[22] R. Tavakkoli-Moghaddam and M. Daneshmand-Mehr, “A computer simulation model for job shop scheduling problems minimizing makespan,” (in English), Computers and Industrial Engineering [Conference Paper] vol. 48, no. 4, pp. 811-823, 2005, doi: 10.1016/j.cie.2004.12.010.

[23] C. R. Harrell, Simulation Using ProModel. McGraw-Hill Education, 2011.

[24] M. S. Casas-Ramírez, J. F. Camacho-Vallejo, and I. A. Martínez-Salazar, “Approximating solutions to a bilevel capacitated facility location problem with customer’s patronization toward a list of preferences,” (in English), Applied Mathematics and Computation, vol. 319, pp. 369-386, 2018, doi: 10.1016/j.amc.2017.03.051.

[25] E. García Dunna, H. García Reyes, and L. E. Cárdenas Barrón, Simulación y análisis de sistemas con ProModel. Pearson Educación, 2013.

[26] E. Orozco-Crespo, N. Sablón-Cossio, R. V. Saraguro-Piarpuezan, D. D. Hermoso-Ayala, and Y. Rodríguez-Sánchez, “Optimización de recursos mediante la simulación de eventos discretos”, Revista Tecnología en Marcha, vol. 32, no. 2, pp. 146-164, 2019, doi: 10.18845/tm.v32i2.4356.

[27] M. S. Casas-Ramírez, J. F. Camacho-Vallejo, R. G. González-Ramírez, J. A. Marmolejo-Saucedo, and J. M. Velarde-Cantú, “Optimizing a Biobjective Production-Distribution Planning Problem Using a GRASP,” Complexity, vol. 2018, p. 3418580, 2018/02/13 2018, doi: 10.1155/2018/3418580.

[28] E. Shokouhi, “Integrated multi-objective process planning and flexible job shop scheduling considering precedence constraints,” (in English), Production and Manufacturing Research, vol. 6, no. 1, pp. 61-89, 2018, doi: 10.1080/21693277.2017.1415173.

[29] D. D. Hermoso-Ayala, “Optimización del proceso de producción de medias corta logo en la fábrica Gardenia”, Bachelor Thesis, Departamento de Ingeniería Industrial, Universidad Técnica del Norte, Ibarra, 2017. [Online]. Available: http://repositorio.utn.edu.ec/handle/123456789/5985

[30] C. J. Barniak-Velalcazar, “Optimización del proceso de abastecimiento de materia prima a las líneas de producción de la empresa Ecuajugos S.A.”, Bachelor Degree, Departamento de Ingeniería Industrial, Universidad Técnica del Norte, Ibarra, 2017. [Online]. Available: http://repositorio.utn.edu.ec/handle/123456789/6905

[31] M. Golari, N. Fan, and T. Jin, “Multistage Stochastic Optimization for Production-Inventory Planning with Intermittent Renewable Energy,” (in English), Production and Operations Management, vol. 26, no. 3, pp. 409-425, 2017, doi: 10.1111/poms.12657.

[32] F. Sánchez-Galván, C. L. Garay-Rondero, C. Mora-Castellanos, D. E. Gibaja-Romero, and H. Bautista-Santos, “Optimización de costos de transporte bajo el enfoque de teoría de juegos. Estudio de caso”, Nova scientia, vol. 9, no. 19, pp. 185-210, 2017, doi: 10.21640/ns.v9i19.1051 

---