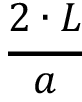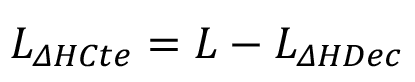Prevención del golpe de ariete mediante el control del tiempo de cierre, al usar válvulas hidráulicas automatizadas

Prevention of water hammer through control of the closing time, in automated hydraulic valves

Gregory Guevara-Rodríguez1, Adrian Vargas-Obando2,
Juan Ignacio Quesada-Chanto3

Fecha de recepción: 9 de noviembre de 2019
Fecha de aprobación: 10 de marzo de 2020

Guevara-Rodríguez, G; Vargas-Obando, A;
Quesada-Chanto, J. I. Prevención del golpe de ariete mediante el control del tiempo de cierre, al usar válvulas hidráulicas automatizadas. Tecnología en Marcha. Vol. 34-1. Enero-Marzo 2021. Pág 143-154.

https://doi.org/10.18845/tm.v34i1.4821

Palabras clave

Golpe de ariete; acueductos; válvulas hidráulicas.

Resumen

Uno de los grandes retos que enfrentamos, al calibrar sistemas automáticos en riego y acueductos, es que la velocidad de los activadores eléctricos es muy rápida, lo que reduce la velocidad de respuesta de las válvulas en términos de apertura y cierre a algunos cuantos segundos. Estos cierres repentinos en la línea de conducción provocan ondas en el interior de la tubería que producen sobrepresiones que pueden generar daños en nuestro acueducto. El presente trabajo ofrece un enfoque alternativo al control y prevención del golpe de ariete, al analizar la relación entre el tiempo de cierre de una válvula en una conducción con pendiente positiva, el respectivo aumento en la línea piozométrica y cómo se puede regular esto mediante la calibración de la velocidad de cierre en el llenado de la cámara superior de las válvulas hidráulicas. Para la comprobación de los resultados, se muestra el caso de un proyecto de invernaderos, hidropónico, que opera con riegos automáticos, donde el tiempo de apertura y cierre de válvulas fue calibrado mediante el control del llenado de las cámaras de las válvulas.

Keywords

Water hammer; aqueducts; hydraulic valves.

Abstract

One of the greatest challenges we face when calibrating automatic systems in irrigation and aqueducts is the high speed of the electric actuators; it reduces the speed of response of the valves in terms of opening and closing to a few seconds. These sudden closures in the line of conduction promote waves inside the pipe that produce overpressures that may generate damages in the aqueduct. The present work is intended to offer an alternative approach to control and prevention of water hammer, by means of the analysis of the relationship between the closing time of the valve, in a conduction with positive slope; the respective increasing in the piezometric line, and how both can be regulated by calibration in the filling speed of the upper chamber of the hydraulic valves. To verify the results, the work shows a case study of a hydroponic greenhouse project that operates with automatic irrigation, where the valves closing time was calibrated by the filling control of the upper chamber of the hydraulic valves.

El fenómeno del golpe de ariete

El golpe de ariete consiste en una alternación de depresiones y sobrepresiones debido al movimiento oscilatorio del agua en el interior de la tubería, producto de variaciones en las velocidades de flujo [1]. El fenómeno se manifiesta como una variación en la presión de la línea de flujo, producida básicamente, tanto en conducciones por gravedad como en sistemas de bombeo presurizado, al forzarse un paro brusco en la inercia del fluido en movimiento dentro de la tubería [2].

El cálculo de las sobrepresiones es importante para determinar las máximas presiones que deberá soportar el tubo; también se debe tomar en cuenta que si las depresiones igualan los valores de tensión del vapor del líquido, se producirá cavitación, incrementando el riesgo de rupturas de la tubería en la fase de sobrepresión [3] [4].

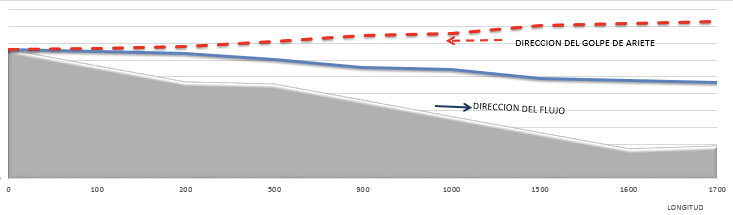
Resulta conveniente identificar un par de diferencias notables en la disposición de la estructura en análisis. Si la tubería va de subida a lo largo de un perfil topográfico, con un sistema de impulsión o bombeo, figura 1(a), el fenómeno se manifestará cuando la unidad de bombeo se detenga en forma no controlada; en el punto más bajo será donde se iniciará el golpe en dirección aguas abajo del bombeo y finalizará en el punto más alto de la conducción; el máximo valor de presión se alcanzará en la misma estación de bombeo. Si por el contrario la tubería va de bajada a lo largo del perfil topográfico, figura 1 (b), el fenómeno se formará en el momento en que se cierre en forma no controlada una válvula en algún punto bajo del perfil topográfico de su conducción, ocasionando un incremento de la línea piozómetrica; por lo tanto, la anomalía se manifestará desde el punto de cierre de la válvula y se desplazará aguas arriba hasta su origen; el máximo valor se alcanzará (registrará) en el punto donde se cerró la válvula [4].

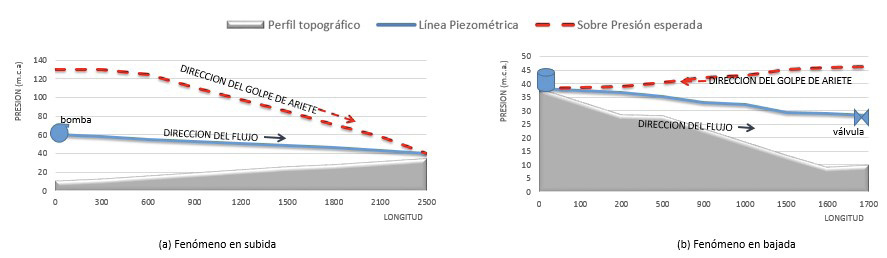
Figura 1. Descripción del golpe de ariete como aumento en la presión en la línea piozómetrica.

Usando el principio de Bernoulli [5], podremos decir que el comportamiento del golpe de ariete como sobrepresión podrá ser calculado de la siguiente forma:

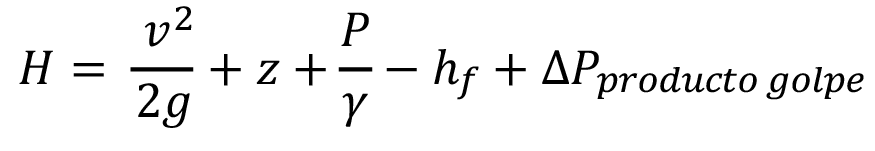
Donde, H es la presión en el tubo y los siguientes términos son con los que normalmente se relaciona u: 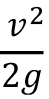es la carga cinética, z es la carga potencial, 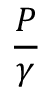es la carga de presión del fluido, menos 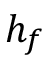son las pérdidas por fricción. Finalmente, el factor 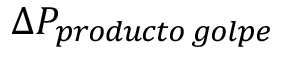es el producto a ese paro repentino, de la inercia en el fluido.

Al analizar que la magnitud numérica de la sobrepresión, producida con el golpe de ariete, depende de varios factores, la relación más directamente observable es con el tiempo en el que se interrumpe la continuidad del flujo, por lo que si tenemos la capacidad de calcular y prevenir las velocidades de cierre de nuestros dispositivos hidráulicos, tendremos la capacidad de control de los dañinos efectos de las sobrepresiones en el golpe de ariete [6], [7].

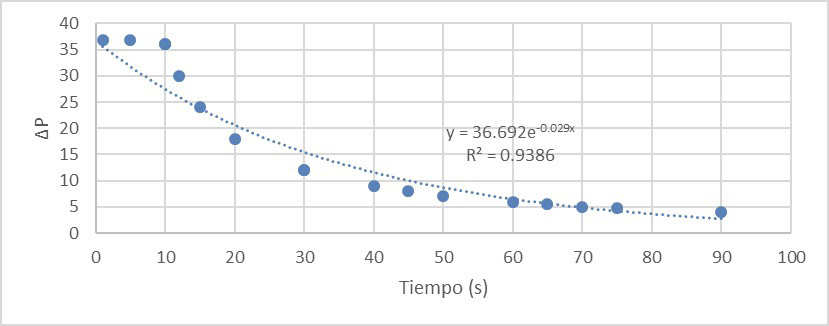
Figura 2 Relación entre la sobrepresión y la velocidad de cierre, en golpes de ariete.

Análisis del comportamiento de la onda

Al ser capaces de calcular el tiempo en que se produce el cierre, la velocidad con que viaja el golpe, sus máximos valores de presión y cómo alteran ellos el comportamiento de la línea piozométrica, o de energía a lo largo del perfil topográfico de nuestra conducción, podremos mediante modelación determinar la relación entre la velocidad de cierre de las válvulas y el efecto que se produce en la magnitud de la sobrepresión a lo largo del tubo [7], [8].

En la figura 3, se expresa el diagrama de flujo de cálculo para la selección de las válvulas hidráulicas, mediante un enfoque en la prevención de los riesgos producto del golpe de ariete.

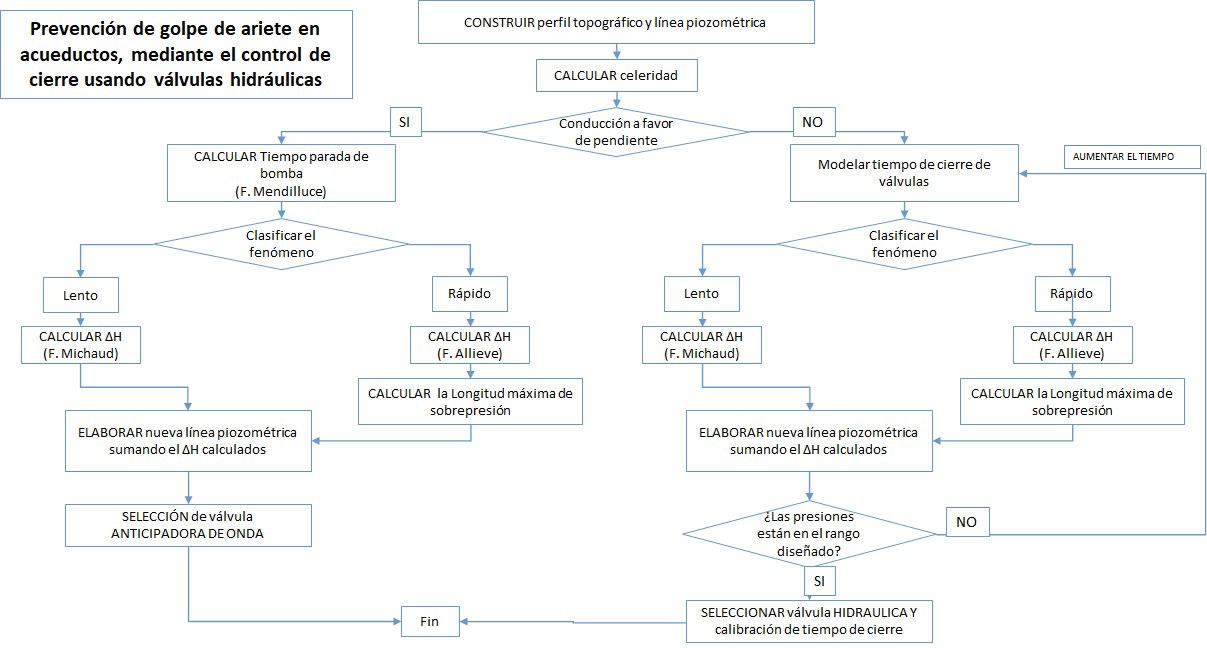
Figura 3 Diagrama de flujo para un nuevo enfoque en la selección de válvulas hidráulicas mediante la prevención del golpe de ariete.

Cálculo de la celeridad y duración del transitorio

La celeridad (a) se define como la velocidad con que se propaga la onda de sobrepresión a través del agua contenida en el tubo, luego de que se genera el fenómeno de cierre de válvula o paro brusco del bombeo [9].

La siguiente es una ecuación deducida para agua, producto de un análisis de la ecuación de movimiento y continuidad:

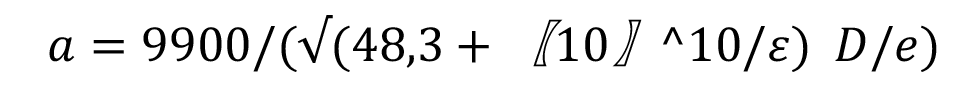
Dónde a es la celeridad en (m/s), D es el diámetro del tubo (mm) y e es el espesor de tubo (mm). ɛ es el módulo de elasticidad (kg/m2). Los valores del módulo de elasticidad de la tubería usada se presentan a continuación:

Cuadro 1. Módulo de elasticidad de materiales [10].

Material de la tubería	ɛ (kg/m2)
Hierro y acero	2x1010
Fundición	1x1010
Hormigón	2x109
PVC	3x108
PE baja densidad	2x107
PE alta densidad	9x107

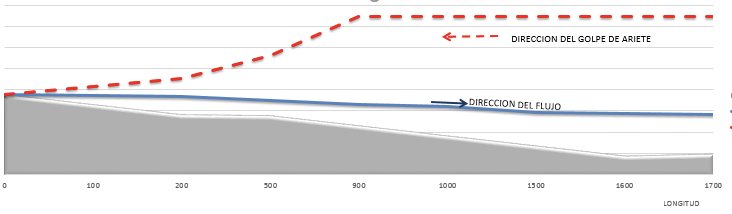
Se entiende que una fase del ciclo del golpe de ariete se da cuando la onda va desde su origen hasta el final de conducción y luego vuelve de nuevo a su lugar de origen. De esta forma, conociendo la longitud del tramo y con la celeridad, analizada anteriormente, nos resulta sencillo despejar el tiempo de duración de la fase (to) en que la onda recorre una distancia L.

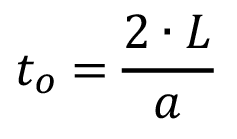
Determinación del tipo de cierre

Joukowski, a finales del siglo XIX, y luego afinado por Allieve en 1903, propuso que el tiempo de duración de la fase (to) es la relación entre la celeridad y la longitud que recorre una onda, siendo esta última dos veces la distancia de la conducción. Ahora que conocemos si el tiempo de cierre de válvula o de parada de bomba es menor o mayor que el tiempo de fase, podremos entender de mejor forma la condición en que se dan las sobrepresiones en la línea [2].

Cierre rápido: Si el tiempo de cierre de válvula o de parada en bomba es menor que el tiempo de fase, estamos en presencia de cierre rápido, debido a que la onda no ha terminado de ir y venir cuando ya se ha detenido totalmente el sistema. Esto quiere decir que la sobrepresión se presentará en cualquier lugar de la conducción y se mantendrá constante hasta un punto específico, que dependerá de la magnitud del golpe [11].

Cierre lento: Si el tiempo de cierre de válvula o de parada en bomba es mayor que el tiempo de fase, estamos en presencia de cierre lento, debido a que la onda ha terminado de ir y venir cuando aún no se ha logrado el cierre total del sistema. En estos casos, la sobrepresión es máxima en el punto de cierre y luego decrece linealmente hasta el origen de la tubería [11].

Comportamiento de la sobrepresión	Tipo de cierre	Criterio de comparación
	Lento	Tc>t0=
	Rápido	TC < t0=

Figura 4. Criterios para el tipo de cierre.

En acueductos donde se aumenta la cota topográfica, el fenómeno del golpe de ariete se dará producto del cierre repentino de la válvula. El golpe, en su máxima magnitud de presión, se manifestará en el punto donde se cierre una válvula, por lo tanto, el tiempo de cierre del sistema será el tiempo que manual, eléctrica o mecánicamente tarde en cerrarse la válvula, por lo que podrá ser manipulado por el usuario [12].

A diferencia de los fenómenos formados en tuberías en bajada, donde fácilmente por medio de un cronómetro se podrá determinar las velocidades de cierre; en las estaciones de bombeo, es más difícil determinar el tiempo de parada de impulsión y su respuesta contra la inercia [13]. Mendiluce [14] propuso la siguiente fórmula empírica para determinar el tiempo de parada de una bomba:

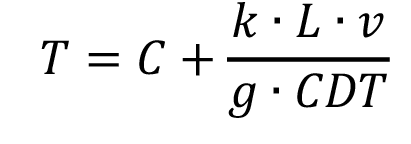
Donde T es el tiempo de parada en segundos, L es la longitud de conducción en metros, v es la velocidad del agua en m/s, g es la aceleración de la gravedad, CDT es la carga dinámica total (m.c.a)

El coeficiente empírico C depende de la pendiente hidráulica, donde

CDT/L < 0,2  C=1

CDT/L ≥ 0,4  C=0

CDT/L ≈ 0,2  C=0,6

El coeficiente empírico k depende de la longitud:

L < 500  k=2

L ≈ 500  k=1,75

500 < L < 1500  k=1,5

L ≈ 1500  k=1,25

L > 1500  k=1

Cálculo de sobrepresiones

Al clasificar los cierres de válvula en los criterios de rápidos y lentos, nos es conveniente analizar el comportamiento de la nueva línea piezométrica, sometido a la onda de sobrepresión producto del paro del sistema. Ahora podremos calcular la máxima magnitud de la sobrepresión en función del tiempo de paro o cierre en el sistema y mediante modelación, planificar diseños en función de las máximas presiones posibles.

En cierre lento, si la velocidad de cierre es menor que el tiempo que dura la onda en ir y venir, se evitará que en algún momento las ondas choquen entre ellas; esto hará que tengamos el punto de máxima energía en el lugar de cierre; de esta forma, la sobrepresión será decreciente desde el final del tubo hacia su origen. La fórmula propuesta por Michaud indica que la sobrepresión dependerá de dos veces la longitud, que es la distancia que recorre la onda, y estará en función del diferencial del cambio en la velocidad, siendo el caso más extremo cuando la velocidad final sea cero, producto de un paro total del sistema [12], [15], [16].

Donde 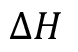es la sobrepresión expresada en metro de columna de agua, L, v, g y T son la distancia, la velocidad, la gravedad y el tiempo de parada respectivamente propuestos para el sistema.

En cierre rápido, a diferencia de los sistemas de cierre lento, las ondas de sobrepresión terminan chocando en el interior del sistema; por lo tanto, la sobrepresión no necesariamente se presenta en el punto de paro, sino que se extiende en forma constante desde el origen del golpe hasta un lugar determinado, por lo tanto, su valor es una constante que no depende de la longitud del tubo [1], [16].

Al igualar ambas ecuaciones de sobrepresión de Allievi y Michaud y despejar su valor de longitud, esta será la distancia desde donde Michaud es máxima y luego empieza a decrecer; por lo tanto, la conoceremos como la longitud de sobrepresión decreciente (LΔHDec)

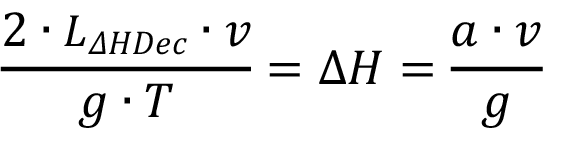
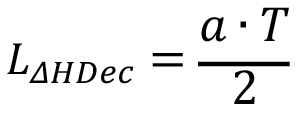
Este valor, longitud de sobrepresión decreciente (LΔHDec), resulta importante en la construcción de la nueva línea piozométrica sometida al fenómeno de golpe de ariete; desde esta ubicación en el acueducto y en el sentido en que la onda se mueva, la magnitud de la sobrepresión siempre irá en descenso. Si estamos en presencia del fenómeno lento, en el sentido más práctico del análisis, este lugar será donde se produce el paro del sistema (apague de bomba o cierre de válvula), y a partir de esta ubicación las sobrepresiones gozarán de magnitudes menores. Bajo condiciones de cierre rápido, sabemos que la máxima magnitud de la sobrepresión se regirá por la fórmula de Allievi; este régimen se extenderá en forma constante, hasta que inicio el régimen de decrecimiento según Michaud; por lo tanto, la longitud de sobrepresión constante (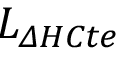), bajo la cual se extenderá el régimen de máxima sobrepresión en regímenes rápidos, estará dada por:

4

Los parámetros de sobrepresión y ubicación nos son de importancia para el análisis del comportamiento del fenómeno y a partir de ahí, para decidir si es conveniente, mediante este proceso de modelaje, inferir sobre las mejores decisiones para la selección y calibración de válvulas.

Control de velocidad de cierre en válvulas hidráulicas

Las válvulas hidráulicas son imprescindibles para solventar un buen número de problemas que se presentan en toda instalación hidráulica: apertura y cierre, regulación de presión aguas arriba y aguas abajo de la válvula y control de boya, entre otras funciones; todas estas aplicaciones en la mayoría de los casos son controladas automáticamente mediante activadores eléctricos o hidráulicos [16]. Estas válvulas en su exterior están constituidas por dos piezas (el cuerpo y la tapa); en su interior se encuentra la membrana o diafragma de caucho, que es el elemento actuante que permite la apertura o cierre al paso del agua. La válvula exterior de tres vías permite la apertura o cierre manual de la válvula, así como la actuación de esta de acuerdo con una señal hidráulica o eléctrica remota [16].

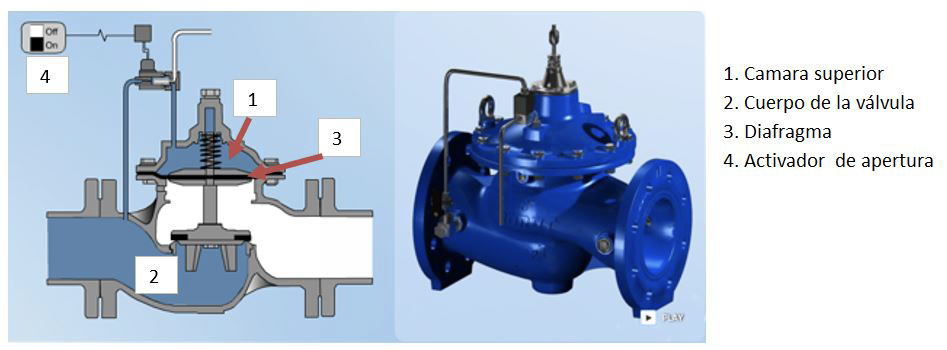
Figura 5. Partes de una válvula hidráulica [19].

Control de la velocidad de llenado de la cámara

La cámara de la válvula (parte superior del diafragma) está conectada a la atmósfera; la presión de agua del interior de la tubería empuja la membrana hacia arriba, abriendo la válvula y por tanto el paso de agua. Cuando se comunica a la cámara de la válvula la presión de agua de la tubería (aguas arriba de la válvula), esta comprime el diafragma hacia abajo, produciendo el cierre completo de la válvula y por lo tanto el corte al paso del agua. Esta operación puede realizarse fácilmente mediante la válvula de 3 vías situada en la tapa de la válvula hidráulica. Este es el funcionamiento de la válvula básica, es decir, abierta-cerrada [16].

Que la válvula se abra o cierre en un determinado tiempo depende directamente de los siguientes factores:

1.La presión del sistema.

2.El volumen de la cámara superior, que debe ser llenado para el cerrado y drenado para la apertura.

3.El diámetro del conducto de llenado o drenado de la válvula.

Al analizar con detalle los factores 2 y 3, que condicionan la velocidad de cierre, observamos que al llenarse la cámara superior, se cierra la válvula, por lo que concluimos que a mayor velocidad de llenado más rápido se cerrará la válvula. Esta es una propiedad que viene intrínseca en el diseño de los elementos hidráulicos que forman la válvula; no obstante, si deseamos aumentar el tiempo de cierre de la válvula, basta con controlar el flujo de ingreso a la cámara.

Para controlar el ingreso de agua a la cámara disponemos de dos alternativas: la primera consiste en una selección del diámetro del tubin que conecta aguas arriba la válvula con la cámara superior. La otra alternativa, sencilla, es la colocación de una válvula de aguja en el tubin que alimenta la cámara, de modo que mediante una contracción en la alimentación de la cámara, podamos reducir el flujo y con esto, aumentar la velocidad de cierre de la válvula.

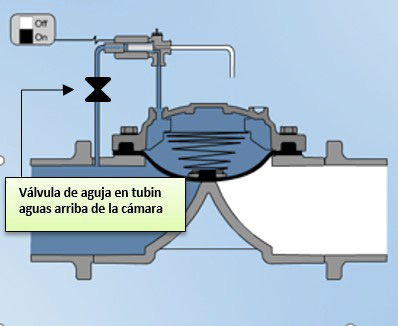
Figura 6. Esquema de ubicación de la válvula de aguja para la calibración de la válvula.

Control de la velocidad con pilotos de cierre uniforme

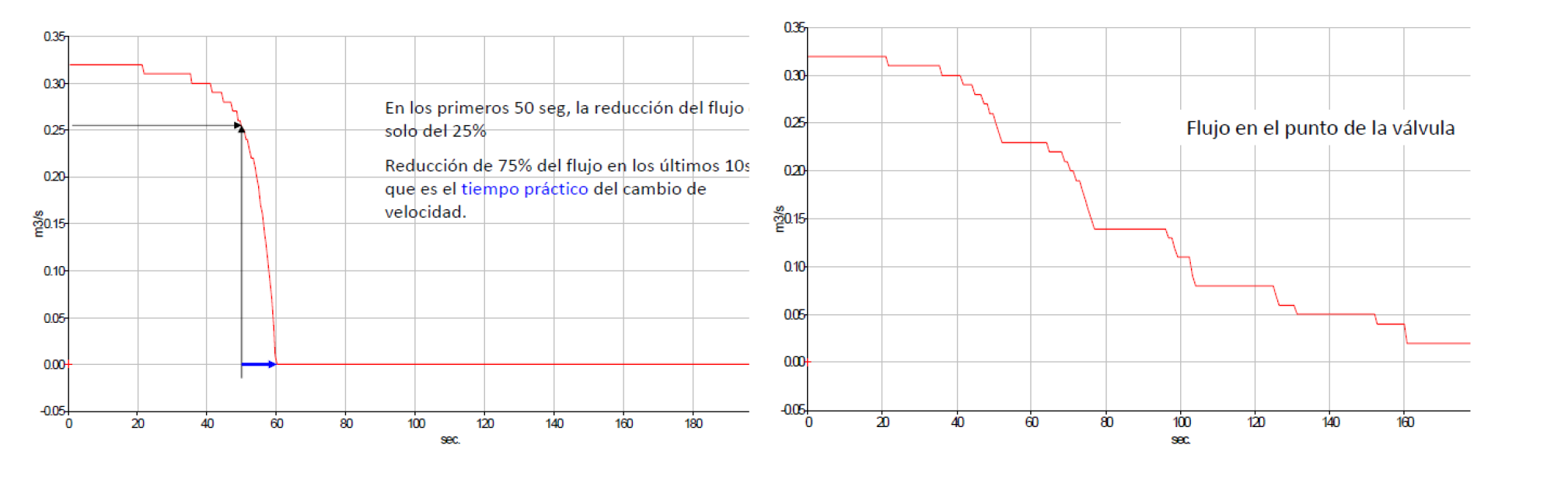
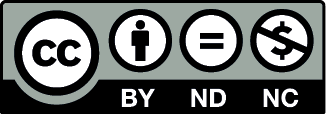
Si bien estos dispositivos mecánicos producen un retardo y una velocidad de cierre uniforme, no garantizan la eliminación de sobrepresiones positivas y negativas en el sistema. En válvulas de control hidráulico con tiempos de cierre uniforme de 60 s, se ha determinado que en los primeros 50 s la reducción del flujo alcanza únicamente el 25%. La reducción del restante 75% del flujo se da en los posteriores 10 s, lapso conocido como tiempo práctico del cambio de velocidad [18].

Gráfica de tiempo de cierre de una válvula estándar	Gráfica de tiempo de cierre de un con piloto con dispositivo SP DOROT

Figura 7. Comparación caudal vrs. tiempo cierre en válvulas estándar y con piloto de cierre constante [20].

Existen pilotos que pueden autoajustar en forma automática y dinámica la velocidad de cierre de las válvulas en cualquier función de control y así resolver las limitaciones de los dispositivos anteriormente mencionados [19].

El comportamiento de los pilotos de cierre lento es similar a lo que se conoce como cierre lineal, cierre que es controlado y postergado en el tiempo [21]. Ante una acción de cierre, el piloto en caso de detectar una presión superior a la calibración, inmediatamente se detendrá; el proceso de cierre se retomará cuando la presión se estabilice y esté por debajo de la presión de calibración. La presión de calibración del piloto se gradúa a 5 m.c.a. por encima de la presión estática del sistema. En caso de presiones excesivas, el piloto ordenará abrir la válvula, la cual funcionará como una válvula de alivio rápido [20].

Caso de estudio

En una red de invernaderos, la fuente de agua, el bombeo y el cabezal de inyección de fertirriego están ubicado en la cota 835 m.s.n.m.; los invernaderos se dispusieron en diferentes terrazas, la primera en la misma cota de la estación de fertirriego y la última en la cota 800 m.s.n.m. Los invernaderos son regados mediante hidroponía en sustrato de coco por goteo autocompensado y autodrenante, con riegos muy cortos, menores de 120 segundos y controlados con válvulas hidráulicas reguladoras de presión (1 válvula por invernadero), accionadas con solenoides de 24 VAC, con un tiempo de cierre de la válvula menor de 2 segundos. Las válvulas manejan en promedio 50 m3/h y son alimentadas por una tubería independiente que lleva el agua con nutrientes desde el cuarto de riego hasta el invernadero en operación. La inyección se da mediante una máquina de fertirriego modelo Netajet High Flow marca Netafim, que regula la proporción de fertilizante en función de valores de pH y conductividad eléctrica preestablecidos.

Durante la operación, debido a los cierres tan rápidos de las válvulas, el sistema elevaba las presiones durante los cierres; esto estaba ocasionando los típicos problemas de ruptura de tubos y accesorios, provocados por el viaje y el golpe de las ondas; pero además ocasionaba que los dispositivos de prevención se abrieran como válvulas de alivio al final de cada riego, lo que conllevaba una serie de problemas operativos: despresurización de la red y goteros antidrenantes, por lo que se perdía tiempo valioso en la respuesta de apertura de los riegos, lo que afectaba el volumen real de agua aplicada. Además, las máquinas de inyección de fertilizante entraban en ciclos de ajuste del caudal, lo que causaba pérdida de precisión en la aplicación del fertilizante, producto de los cambios en las conductividades eléctricas. En la figura 8 se muestra el comportamiento de la variación de los volúmenes aplicados, producto del golpe que abría las válvulas de alivio.

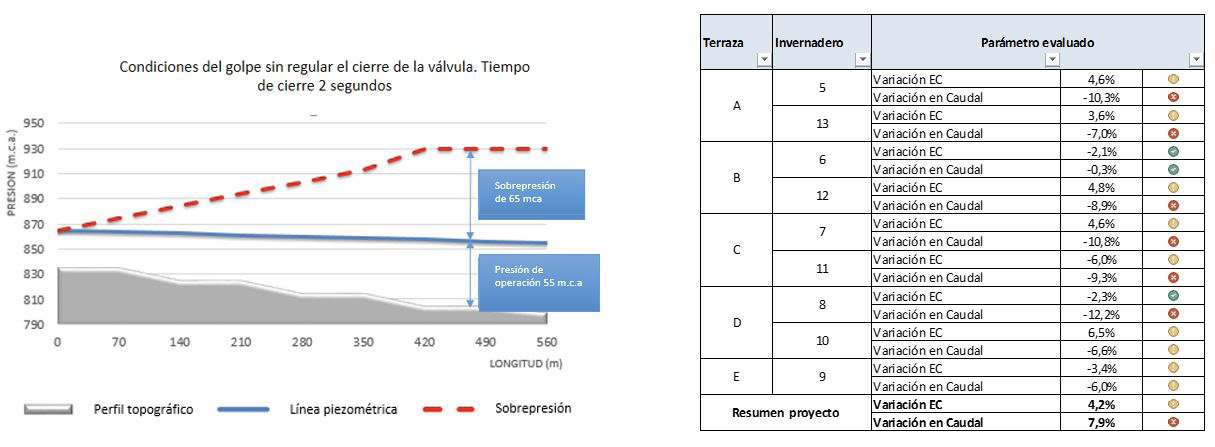
Figura 8. Tablero de control con los resultados de operación del fertirriego, antes de regular el cierre de válvulas.

Se procedió a una modelación y ajuste del tiempo de cierre de válvulas, usando válvulas de aguja en el tubin que llena la cámara hidráulica. El criterio buscado fue que la válvula cerrara tan rápido como para manejar un adecuado control del tiempo de riego, pero no tan rápido como para que disparara las válvulas de alivio por la sobrepresión y evitar que estas últimas causaran problemas estructurales en las tuberías. En este caso, se usó tubería de 4” SDR 32,5, con una presión máxima operativa de 8,8 bares. Se decidió que el mínimo tiempo que podríamos operar el cierre de la válvula sería de 6 segundos, para no causar sobrepresión que superara la capacidad del tubo. Se reguló el cierre de todas las válvulas en ese tiempo. Los resultados en uniformidad de caudal y conductividad fueron absolutamente positivos. En la figura 9 se muestra la respuesta después de variar el tiempo de cierre a 6 segundos, evitando presiones críticas que disparan las válvulas de alivio.

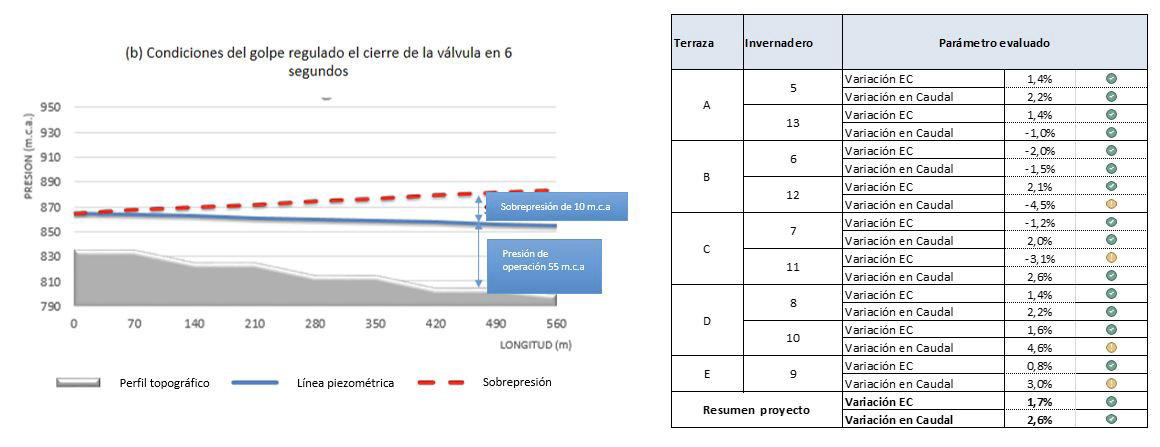
Figura 9. Tablero de control con los resultados de operación del fertirriego, luego de calibrar el tiempo de cierre de las válvulas en 6 segundos.

Conclusiones

Mediante el empleo de las ecuaciones actuales de la mecánica de fluidos y el análisis de línea de energía o piozométrica de un acueducto, es posible realizar el análisis de las sobrepresiones en el golpe de ariete, en función del tiempo de apertura de las válvulas. Conocer las magnitudes en que las ondas de presión viajan durante el fenómeno del golpe de ariete nos resulta útil para colocar los dispositivos adecuados, capaces de mitigar o controlar sus efectos, y si podemos controlar el tiempo en que se desarrolla el golpe de ariete, podremos reducir los posibles daños que enfrentar.

Con el presente enfoque metodológico se busca mediante un modelado hidráulico y un proceso de calibración de las válvulas en campo, poder reducir los daños ocasionados durante un transitorio, por el súbito cierre de los activadores de alta velocidad presentes en el mercado.

Para un mejor entendimiento del tema es importante abordar otros análisis como el tiempo de duración de la onda, la magnitud y la cantidad de réplicas que siguen a la primera onda, así como otros datos que completarán el análisis del fenómeno.

Referencias

[1] J. Twyman, “Golpe de ariete en una red de tuberías debido al cierre rápido de una válvula,” Revista de Ingeniería en Construcción, vol. 33, no. 2, 2018.

[2] R. Mott and J. Untener, Applied Fluid Mechanic, 7th ed. USA: Pearson, 2015.

[3] A. Malekpour, B. Karney, R. St. Aubin, P. Martino, and L. Gill, “Exploring the sensitivity of fatigue analysis with regard to design parameters in PVC pipes subjected to cyclic transient pressures,” Procedia Engineering, vol. 119, pp. 174-181, 2015.

[4] W. Wan and B. Zhang, “Investigation of water hammer protection in water supply pipeline sytems using an intelligent self-controlled surge tank,” Energies, pp. 11-16, 2018.

[5] Universidad de Oviedo, “Práctica de laboratorio: golpe de ariete”, en Curso de especialidad en centrales eléctricas, Oviedo, 2010.

[6] R. Nerella and E. Rathnam, “Fluid transients and wave propagation in pressurized conduits due to valve closure,” Procedia Engineering, vol. 127, pp. 1158-1164, 2015.

[7] B. Jung and B. Karney, “A practical overview of unsteady pipe flow modeling: From physics to numerical solutions,” Urban Water Journal, vol. 14, no. 5, pp. 1-7, 2016.

[8] S. Manbretti, Water Hammer Simulations. Brasil: WIT Press, 2015.

[9] J. Twyman, “Golpe de ariete en una red de distribución de agua,” XXI, PAIDEIA, vol. 6, pp. 53-68, 2018.

[10] J. Callister and William D, Fundamentals of Materials Science and Engineering. USA: John Wiley & Sons, 2005.

[11] I. Pothof and B. Karney, “Guidelines for transient analysis in water and distribution systems”, Intech, 2013.

[12] J. Yu, Z. Wu, Y.-X. Yuan, M. Zhao, and C.-G. Wu, “Optimal valve closure for long-distance water transmission,” Sustain. Environ. Res., vol. 20, no. 5, pp. 287-291, 2010.

[13] G. Z. Watters, Analysis and control of unsteady flow in pipes, 2nd ed.. USA: Butterworths, 1984.

[14] W. Wan, B. Zhang, and X. Chen, “Investigation on water hammer control of centrifugal pumps in water supply pipeline systems,” Energies, no. 12, 2019.

[15] J. Twyman, “Interpolation schemes for valve closure modelling,” Ingeniare, Revista Chilena de Ingeniería, vol. 26, no. 3, 2018.

[16] K. A., “An analysis of the impact of valve closure time on the course of water hammer,” Archives of Hydro-Engineering and Environmental Mechanics, vol. 63, no. 1, pp. 35-45, 2016.

[17] Y. Dvir, “FLow control devices,” Israel: Bermad, 1995.

[18] Bermad Company, “Hydraulic valve for control,” Israel: Irrigation, 2015.

[19] Dorot, Control Valves, “Control de niveles en reservorios,” Boletín Técnico Dorot, vol. 11, 2017.

[20] G. Heimann, “Water Hammer,” in Seminario Latinoamericano Válvulas Hidráulicas Dorot, Tel Aviv, Israel, 2018.

[21] T. Janus and U. B., “Hydraulic modelling for pressure reducing valve controller design,” Procedia Engineering, vol. 186, p. 635 – 642 , 2017.

---