Comparación entre el índice de confiabilidad y capacidad de carga para la evaluación de seguridad estructural en puentes utilizando pruebas de carga de diagnóstico: Caso de estudio en Costa Rica
Comparison between reliability index and load rating for evaluation of structural security of bridges using diagnostic load tests: Case of study in Costa Rica
Darnel G. Bolaños-Ávila1
Fecha de recepción: 26 de agosto de 2018
Fecha de aceptación: 29 de noviembre de 2018
Bolaños-Ávila, D. Comparación entre el índice de confiabilidad y capacidad de carga para la evaluación de seguridad estructural en puentes utilizando pruebas de carga de diagnóstico: Caso de estudio en Costa Rica. Tecnología en Marcha. Vol. 32-3. Julio-Setiembre 2019. Pág. 55-65.
DOI: https://doi.org/10.18845/tm.v32i3.4479
Palabras clave
Capacidad de carga; índice de confiabilidad; confiabilidad estructural; prueba de carga de diagnóstico; puente.
Resumen
En el presente trabajo se aplican dos métodos de evaluación de seguridad estructural (capacidad de carga e índice de confiabilidad) sobre el mismo puente al cual se le aplicó una prueba de carga de diagnóstico con dos configuraciones de posición de los camiones. El objetivo es comparar los resultados y, discutir acerca de las limitaciones de cada uno y finalmente recomendar casos donde cada método es más útil. Asimismo, recalcar el beneficio que se pueden obtener al emplear las pruebas de carga para la evaluación de la condición de los puentes con respecto a la metodología que se usa en Costa Rica. Los métodos son evaluados por falla a flexión en las vigas de concreto presforzado. Además se desarrolló un modelo del puente en el software CSi Bridge 2017® para comparar los resultados esperados con los obtenidos en la prueba de carga. Los resultados demuestran que el puente tiene marcadas diferencias entre las deformaciones teóricas y las reales, debido a la rigidez de elementos no estructurales. El puente se encuentra en condición excelente, según ambos métodos. Se concluye que para la evaluación de seguridad estructural, el índice de confiabilidad es el más indicado por las correlaciones intrínsecas para cada puente.
Keywords
Load rating; reliability index; structural reliability; diagnostic load test; bridge.
Abstract
In the present work two methods for structural safety evaluation are applied (load rating and reliability index) on the same bridge which was applied a diagnostic load test with two different configurations of truck’s position. The aim is to compare the results and discuss about the limitations of each one and finally recommend cases where each method is more useful. Likewise accentuate the benefits of using load test for bridge condition evaluation with respect to the methodology that is in use in Costa Rica. The methods were evaluated for failure of flexure on the prestressed concrete beams. Besides it was developed a bridge model in the software CSi Bridge 2017® to compare the expected results with the obtained in the load test. The results show that the bridge has differences between the theoretical and real deformations, due to the stiffness of non-structural elements. The bridge has an excellent condition according to both methods. It concludes that the reliability index is better for structural safety evaluation, for its correlations for each bridge.
Introducción
En Costa Rica, para la revisión de la condición de un puente, se cuenta únicamente con el ‘Manual de Inspección de Puentes’ del Ministerio de Obras Públicas y Transportes, como guía normada [1]. El manual establece pautas para la realización de inspecciones visuales en los puentes y, a partir de los informes generados en las inspecciones, la plataforma SAEP2 prioriza las estructuras para las acciones de rehabilitación [2]. Esta metodología es incompleta, puesto que tiene dos desventajas principales: la variación en la valoración de daños por parte de diferentes inspectores es alta, por lo que se resalta la dificultad de obtener objetividad en las evaluaciones visuales [3]; por otro lado, no se considera ningún análisis estructural las condiciones de servicio (carga viva), por lo que la evaluación del SAEP no describe la condición de seguridad estructural del puente a nivel de sistema o elemento [2], lo cual es fundamental, ya que la sobrecarga es una de las causas de colapso de puentes principales en Costa Rica [5].
Por tanto, diferentes técnicas han sido realizadas en el país para solventar esas desventajas y obtener un resultado de seguridad estructural más objetivo, como el desarrollo de metodologías de inspección visual más detalladas [2], pruebas de carga [4, 6], monitoreo estructural [5], entre otros. Este artículo tiene por objetivo principal presentar dos métodos (índice de confiabilidad y capacidad de carga) comúnmente utilizados para evaluar la seguridad estructural de los puentes [3, 4, 7 – 13] a partir de los datos registrados en una prueba de carga de diagnóstico realizada en un puente en Costa Rica y, comparar la representatividad que tienen los resultados para evaluar la seguridad. Asimismo, se analiza la comparación de los resultados de prueba de carga con los del modelo teórico elaborado en CSi Bridge 2017®.
Cuadro 1. Errores en mediciones de deformación
|
Causa de error |
Mínimo |
Máximo |
Referencia [ver en 10] |
|
Sensor |
1.00% |
3.00% |
Bäumel (2006) |
|
Desalineación |
0.00% |
3.00% |
Vishay (2007) |
|
Desviación lineal |
0.03% |
0.10% |
Hesse (2006) |
|
Creep |
Evitable |
Evitable |
DMS-Katalog (2007) |
|
Fatiga (ciclo) |
Evitable |
Evitable |
DMS-Katalog (2007) |
|
Cable de sensores (ruido) |
0.14% |
0.30% |
Bäumel (2006) |
|
Sistema de adquisición de datos |
0.03% |
0.05% |
Bäumel (2006) |
|
Aplicación |
0.00% |
Depende de usuario |
Klarer (2007) |
Adaptado de Frangopol et. al, 2008.
Prueba de carga de diagnóstico
La prueba de carga de diagnóstico, es una observación y medición del comportamiento de diferentes elementos de un puente ante controladas y predeterminadas cargas que no afectan la respuesta elástica [14]. Los parámetros de deformación y aceleración son los que se miden usualmente, en los elementos principales, sin embargo, también se puede medir el desplazamiento en las juntas de expansión o en los apoyos; por medio de sensores [3, 4, 10]. Su mayor uso radica en la verificación del comportamiento en contraste con el modelo teórico y su posterior calibración, debido a que la rigidez que aporta los elementos no estructurales o el deterioro progresivo, implican que las cargas se distribuyan de forma diferente a la predicha [5, 16]. No obstante, los sensores tienen errores en la medición como cualquier otro instrumento, en el cuadro 1 se muestran distintos errores expresados en porcentaje de afectación [10].
Capacidad de carga
El método de capacidad de carga (mejor conocido como Load Rating) fue propuesto por la AASHTO [14] y utiliza un factor que relaciona la resistencia remanente entre la carga viva. Los encargados de los puentes, lo emplean para asegurar la resistencia ante una determinada carga, por lo cual, es usado como homólogo de la seguridad estructural de un puente [7]. Posee un enfoque pseudo-determinístico, por lo que solo evalúa un caso de carga – resistencia por vez. Debido a esta característica, se emplean factores prestablecidos de mayorización de cargas y reducción de resistencia para contemplar la variabilidad de los parámetros (ecuación 1).
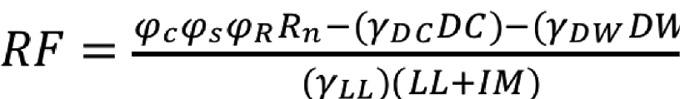 (1)
(1)
Donde, RF: factor de capacidad de carga teórico; φ(C, S, R): Factor de condición, sistema y resistencia respectivamente [ver en 14]; Rn: resistencia nominal del elemento; γ (DC, DW, LL): factor de mayorización de carga muerta de componentes estructurales (1.25), carga muerta de accesorios (1.5 o 1.25 si la superficie de ruedo es verificada en campo) y carga viva (1.75 para inventario y 1.35 para operación), respectivamente; DC: efecto por carga muerta de elementos estructurales; DW: efecto por carga muerta de accesorios; LL: efecto por carga viva; IM: efecto por impacto (se utiliza entre 10% - 20% de la carga viva [14]). Si RF ≥ 1, entonces el elemento se concluye como seguro, mientras que si RF < 1, el elemento falla ante la carga impuesta.
De igual manera, el factor se puede adaptar a los resultados de una prueba de carga de diagnóstico, a través de un factor K (ecuación 2 y 3), que relaciona las deformaciones teóricas con las deformaciones medidas por medio de Ka (ecuación 4) y el nivel de confianza en los resultados representado por Kb.
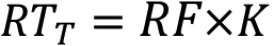 (2)
(2)
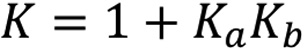 (3)
(3)
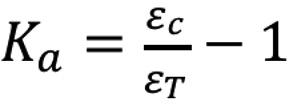 (4)
(4)
Donde, Ka: considera la diferencia entre las deformaciones medidas y las esperadas; Kb: considera el entendimiento de los resultados; εC: deformación teórica cuando el camión de carga teórica está en la misma posición que el camión de carga de la prueba; εT: máxima deformación medida en la prueba.
El término Kb es determinado considerando el momento teórico producido por el camión de la prueba de carga (T) y el momento teórico más impacto, producido por el camión teórico (W) [3]. El objetivo es comparar la carga de prueba con la carga teórica para asegurar la extrapolación del comportamiento. Un Kb de 0.8 es asignado por T/W mayor a 0.4; de 1 para T/W mayor a 0.7 y de 0 para T/W menor a 0.4 [14].
Índice de confiabilidad
El índice de confiabilidad es un método que considera las variables de entrada, tanto de resistencia como de efecto de carga, como variables aleatorias; por lo que siguen una distribución de probabilidad definida. Tiene un enfoque estocástico, por tanto, en su resultado es contemplado diversos escenarios de carga – resistencia que se evalúan por la función de estado límite (g = R-L) [9, 10]. El índice de confiabilidad se define como la distancia, en términos de la desviación estándar, entre el valor medio de la función de estado límite y el margen de seguridad (g = 0) [12]. Si la resistencia y la carga siguen una distribución normal, el índice de confiabilidad se expresa con la ecuación 5. Los resultados de g < 0 son los que determinan la probabilidad de falla de la estructura (figura 1), la cual se puede expresar en términos del índice de confiabilidad (ecuación 6).
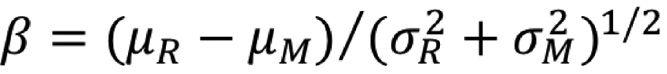 (5)
(5)
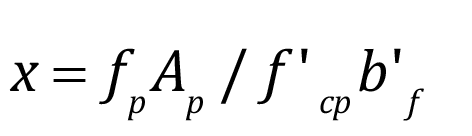 (6)
(6)
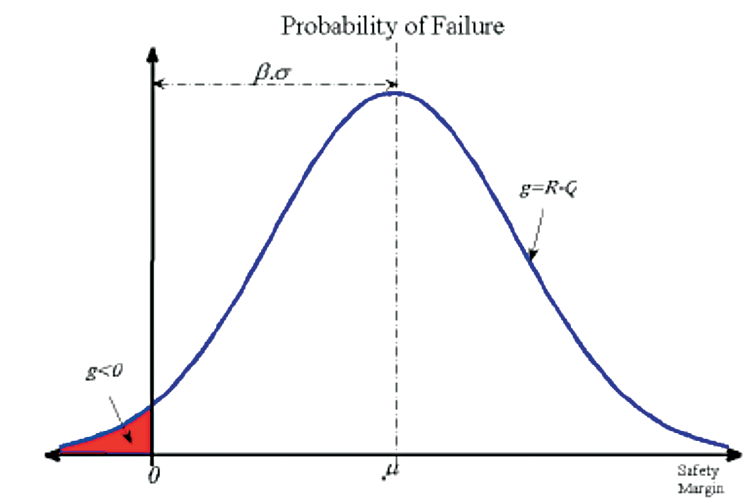
Figura 1. Relación gráfica entre la probabilidad de falla e índice de confiabilidad [12].
Donde, β: índice de confiabilidad; μR, μQ: media de la resistencia y el efecto de la carga; σR, σQ: desviación estándar de la resistencia y el efecto de la carga; Φ: función de probabilidad estándar normal.
Los errores presentados en el cuadro 1, se pueden tomar en cuenta con el factor es que suma los porcentajes de errores contemplados por el usuario. Por lo tanto el índice de confiabilidad se expresa como se muestra en ecuación 7 [10].
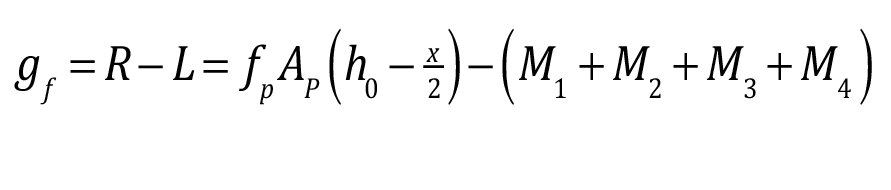 (7)
(7)
El estado de un puente de acero o concreto, se puede clasificar con base en el índice de confiabilidad. Con β < 4,6 es inaceptable; 4,6 ≤ β < 6,0 es aceptable; 6,0 ≤ β < 8,0 es bueno; 8,0 ≤ β < 9,0 es muy bueno y 9,0 ≤ β es excelente [8].
Metodología – Caso de estudio
El caso de estudio se centra en un puente construido en 2016. Tiene una luz de 20.5 m de longitud y 8.975 m de ancho (detalles en figura 2). Cuenta con 7 vigas tipo I prefabricadas de concreto presforzado de 1.2 m de peralte y separadas 1.2 m de centro a centro; 3 diafragmas; 3 diafragmas (1 en cada apoyo y al centro) de 0.9 m de peralte. Una losa de 18 cm de espesor promedio de concreto reforzado, sin capa de asfalto. Posee apoyos de neopreno reforzado con 3 láminas de acero, sobre bastiones de concreto reforzado.
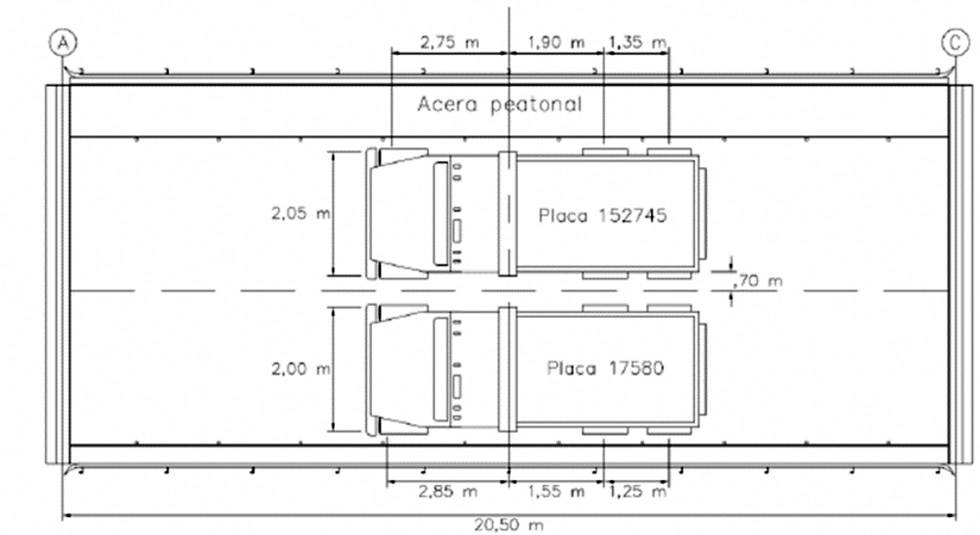
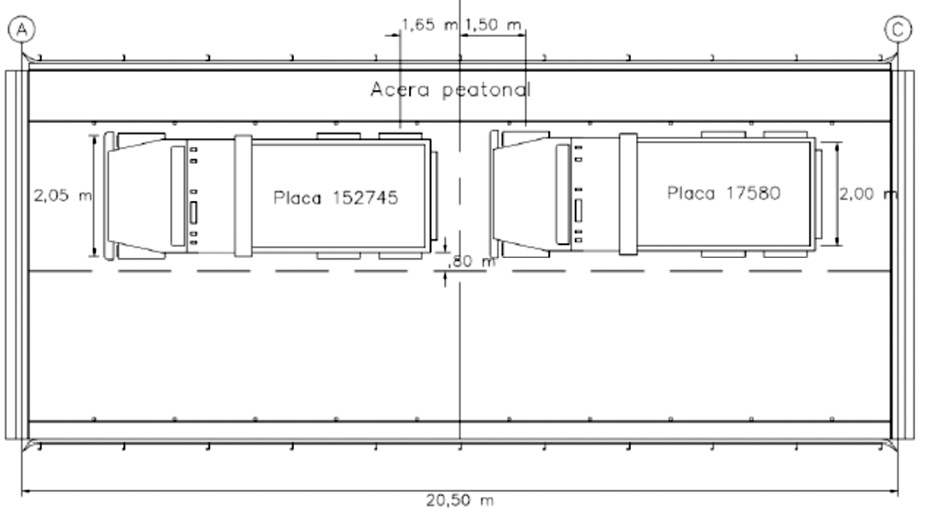
La prueba de carga de diagnóstico fue realizada en febrero de 2017 por el equipo de eBridge del Tecnológico de Costa Rica. Fueron medidas las deformaciones de las 7 vigas principales. Sin embargo, la viga N°2 tuvo problemas con la instalación del sensor, por lo cual los datos fueron descartados. Se utilizaron dos camiones con ejes triaxiales (cuadro 2). Dos casos de carga fueron efectuados, como se muestra en la figura 3a y 3b; donde el Caso I se colocó los camiones en ambos carriles y en el Caso II se dispusieron solamente el carril derecho.
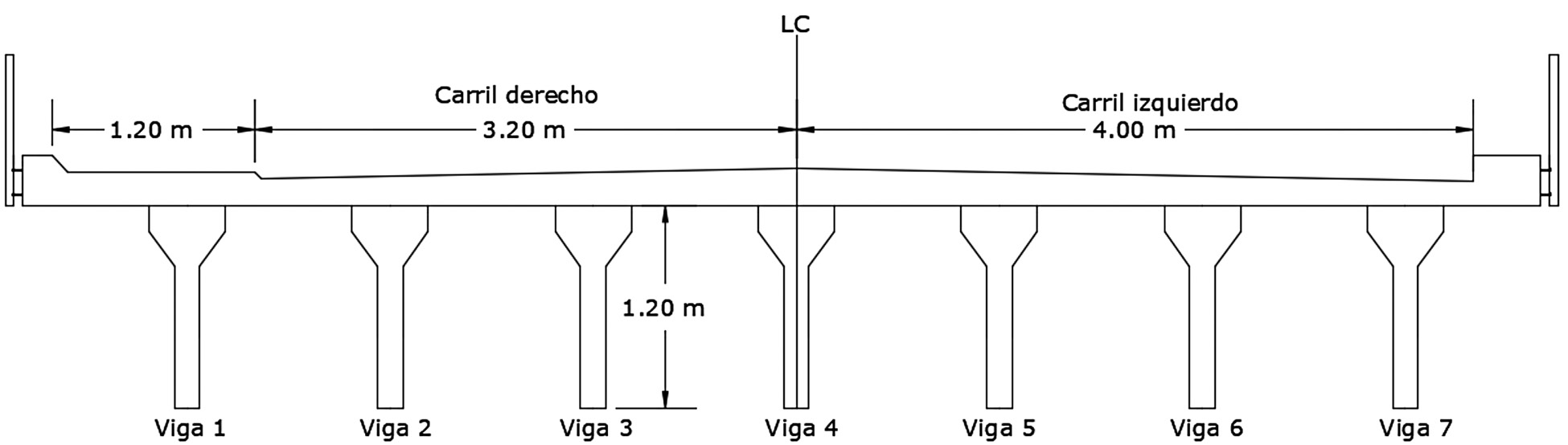
Figura 2. Sección transversal del puente de caso de estudio.
Además fue desarrollado un modelo en 3 dimensiones en el software CSi Bridge 2017®, para determinar las deformaciones teóricas por los camiones de prueba y, calibrar el factor de capacidad de carga. Las almohadillas de neopreno fueron modelados como resortes cuya rigidez axial, cortante y rotacional fue calculada para representar el comportamiento de apoyo. Los elementos no estructurales (acera peatonal, soportes de baranda y barandas) fueron incluidos como cargas distribuidas superficiales, no como elementos. El modelo no considera ningún tipo de deterioro.
Ambos métodos fueron evaluados para el estado límite de falla por flexión en las vigas principales (ecuaciones 8 y 9), donde el momento por carga viva es calculado con base en las deformaciones obtenidas en la prueba de carga. La desviación estándar se calculó a partir un supuesto coeficiente de variación presentado de un caso similar en la referencia [13] debido a que no se contaba con ensayos para determinar los parámetros reales de los materiales. En el cuadro 3 se muestran los datos estadísticos usados para realizar una simulación de Monte Carlo de 10.000 iteraciones con el fin de elaborar una distribución de probabilidad normal que describa las variables aleatorias de entrada (resistencia a la compresión del concreto, resistencia a tracción y área transversal del acero de presfuerzo y altura efectiva), las cuales fueron elegidas debido a su mayor probabilidad de variación en el tiempo o proceso de construcción. De igual manera se hizo una simulación para los datos estadísticos obtenidos en la prueba de carga en las diferentes vigas. La capacidad de carga se evaluó para una condición de operación y, no se considera el impacto, debido a que la prueba de carga fue estática. El índice de confiabilidad fue evaluado considerando un 3% de error en los sensores, puesto que el autor no estuvo presente en la ejecución de la prueba y se opta por ser conservador.
Cuadro 2. Datos de carga de ejes de camiones usados en la prueba
|
Placa |
Carga eje frontal |
Carga primer eje trasero |
Carga segundo eje trasero |
PTV1 |
|
152745 |
5.96 ton |
10.10 ton |
10.10 ton |
26.16 ton |
|
17580 |
6.20 ton |
10.80 ton |
10.80 ton |
27.80 ton |
1PTV = Peso total de vehículo.
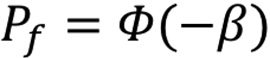 (8)
(8)
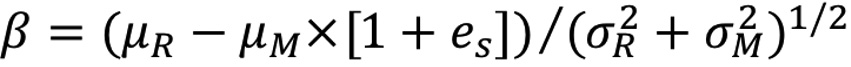 (9)
(9)
Donde, x: zona en compresión; fp: resistencia a la tracción del acero de presfuerzo; Ap: área de sección de la barra de presfuerzo; f’cp: resistencia a la compresión del concreto de las vigas; b’f: ancho en compresión; b: espesor del alma de la viga; h’f: espesor promedio de ala de la viga; h0: altura efectiva de la sección de viga; M1-4: momento debido a carga muerta de elementos estructurales, accesorios, carga viva e impacto; respectivamente.
Resultados
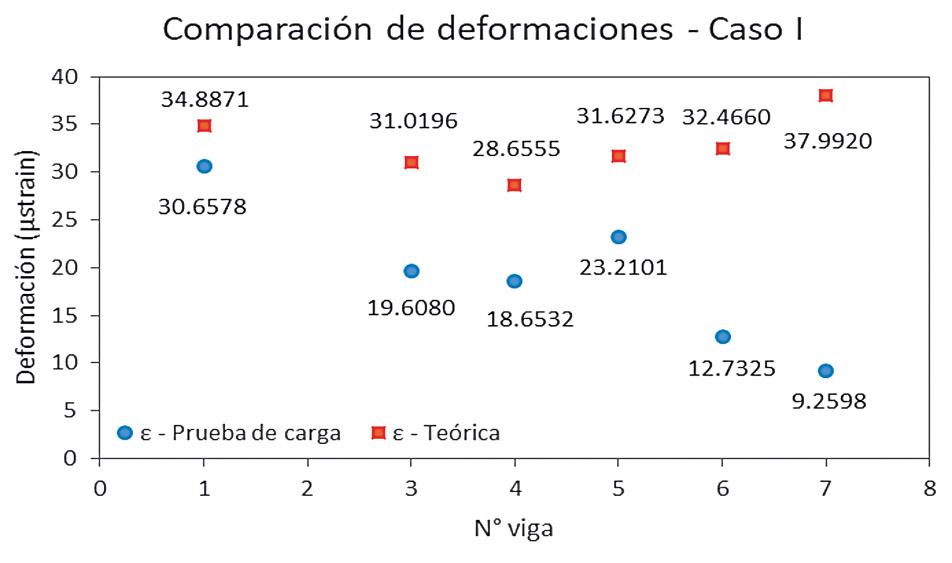
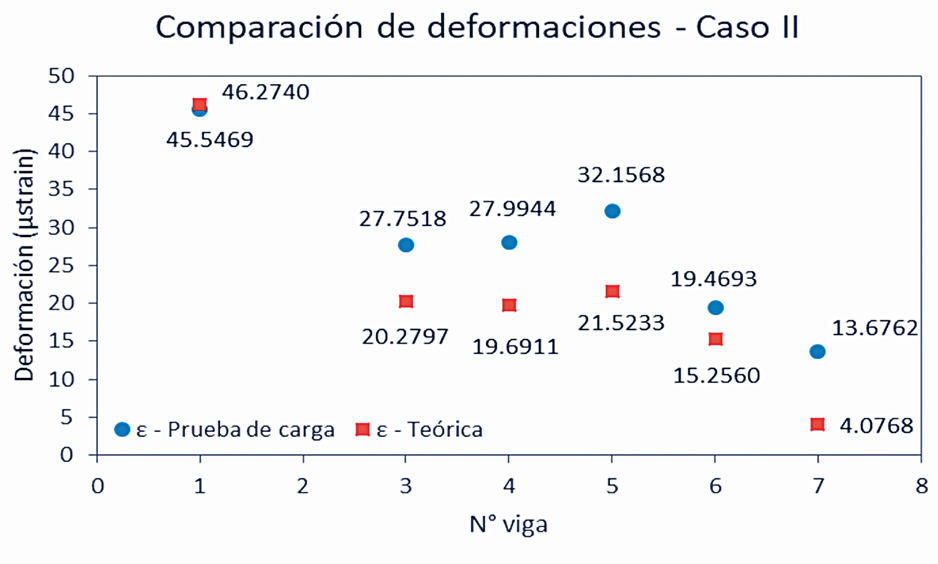
Los resultados de las deformaciones del modelo teórico y la prueba de carga de diagnóstico se muestran en las figuras 4a y 4b. En el Caso I, las deformaciones teóricas están por encima de las deformaciones reales, lo que implica que el puente se comporta de mejor manera a lo esperado teóricamente. Sin embargo, se denota que los puntos de deformaciones no siguen la misma tendencia; mientras que el modelo tiene una ‘simetría en forma de v’, la deformación real presenta un comportamiento distinto, donde se destacan las vigas 6 y 7, que se predecían como las más deformadas del sistema y resultan como las menos deformadas, con más de 150% de diferencia. Por otro lado, en el Caso II, las deformaciones teóricas son inferiores a las reales, lo que indica que el puente se comporta más crítico que lo esperado. Se observa que en este caso la tendencia es similar y las diferencias no son tan críticas como el Caso I.
Cuadro 3. Estadística descriptiva de variables aleatorias
|
Variable |
Tipo de distribución [13] |
Media [6] |
Coeficiente de variación [13] |
Desviación estándar |
|
f’cp [kg/cm2] |
Normal |
600 |
0.0344 |
20.640 |
|
Ap [cm2] |
Normal |
12.87 |
0.0080 |
0.10296 |
|
dp [cm] |
Normal |
102.5 |
0.0021 |
0.21525 |
|
fp [kg/cm2] |
Normal |
18900 |
0.0101 |
190.89 |
|
R [ton-m] |
Normal |
245.21 |
- |
3.173 |
(a) (b)
Figura 3. Colocación de camiones para prueba de carga de diagnóstico, a) Caso I; b) Caso II [6].
Las diferencias encontradas entre el modelo teórico y la prueba de carga, se deben a diferentes factores, especialmente la rigidez real del puente [3, 10, 15] que no es reflejada en el modelo teórico, al considerar solamente como cargas los elementos no estructurales, por lo cual la trayectoria de las cargas puede variar significativamente, puesto que depende exclusivamente de la rigidez de los elementos, ya que las cargas tienden a moverse a través de los elementos más rígidos [16]. En el Caso I, el lado derecho al poseer la acera peatonal de concreto y un carril más angosto, tiene mayor rigidez que el lado izquierdo, por lo cual la viga 1 tiende a recibir más carga que la viga 7, por ejemplo. En el Caso II, los ejes de los camiones están más cerca de los puntos de medición de los sensores, por lo cual, la acción de la rigidez del diafragma central [3, 15] es un factor determinante para que las vigas se esforzaran más que el modelo teórico.
En la figura 5, se muestra el resultado del método de capacidad de carga calibrado por medio del factor K, para las 6 vigas analizadas en el Caso I y Caso II. Se destaca principalmente la diferencia entre los casos, puesto que el Caso I obtuvo un factor K mayor o igual a 1 en todos las vigas, por lo que el RF teórico aumenta; contrario al Caso II donde el factor K es menor que 1, por consiguiente el RF teórico disminuye. El impacto de este factor se refleja con más claridad en la viga 1 y 7, donde el primer caso la diferencia de deformaciones es de 15 μstrain y el RF solo difiere en 1 unidad aproximadamente, mientras que en la viga 7 los resultados de deformación distan por 4 μstrain, pero el RF del Caso I es más de 4 veces el RF del Caso II. A pesar de eso, todos cumplen con un RF > 1, donde el más crítico es 1.501, lo que implica que resiste un 50% más de la carga impuesta.
(a) (b)
Figura 4. Comparación de deformaciones teóricas y reales, a) Caso I; b) Caso II.
Por otro lado, en la figura 6 se encuentra los resultados de los índices de confiabilidad para las 6 vigas y ambos casos. Es distinguible que, a diferencia del método de capacidad de carga, la diferencia entre los resultados de ambos casos es pequeña. Esto se debe a que el modelo teórico no tiene influencia en este método, por lo que únicamente toma en cuenta el efecto de momento ejercido por los camiones en su estado límite y las variaciones de carga y resistencia, por lo que el Caso II afecta ligeramente más al puente que el Caso I en todas las vigas. La probabilidad de falla es tendiente a ٠٪ y se denota que el valor crítico del índice de confiablidad (٣٢.٨٢٥١) es muy superior al recomendado por [٨] como una condición excelente del puente (β > 9.0).
La capacidad de carga posee un enfoque determinístico y el índice de confiabilidad un enfoque probabilístico [7]. Por tanto, la consideración de la variación de la carga y resistencia, es una marcada diferencia entre ambas metodologías, debido a que el RF busca un resultado crítico al aumentar las cargas y disminuir la resistencia con factores fijos. Por otro lado, el β utiliza las desviaciones estándar de los parámetros que conforman la ecuación de resistencia y los datos estadísticos obtenidos en la prueba de carga, que se determinen como variables aleatorias, lo que implica que considera casos donde la carga y la resistencia pueden adoptar valores altos y bajos; además se obtiene un comportamiento más ‘personalizado’ de los materiales del puente, ya que es los valores de incertidumbre pueden ser completamente diferentes para un puente de concreto que de acero, mientras que el RF puede adoptar el mismo factor de reducción de resistencia para ambos.
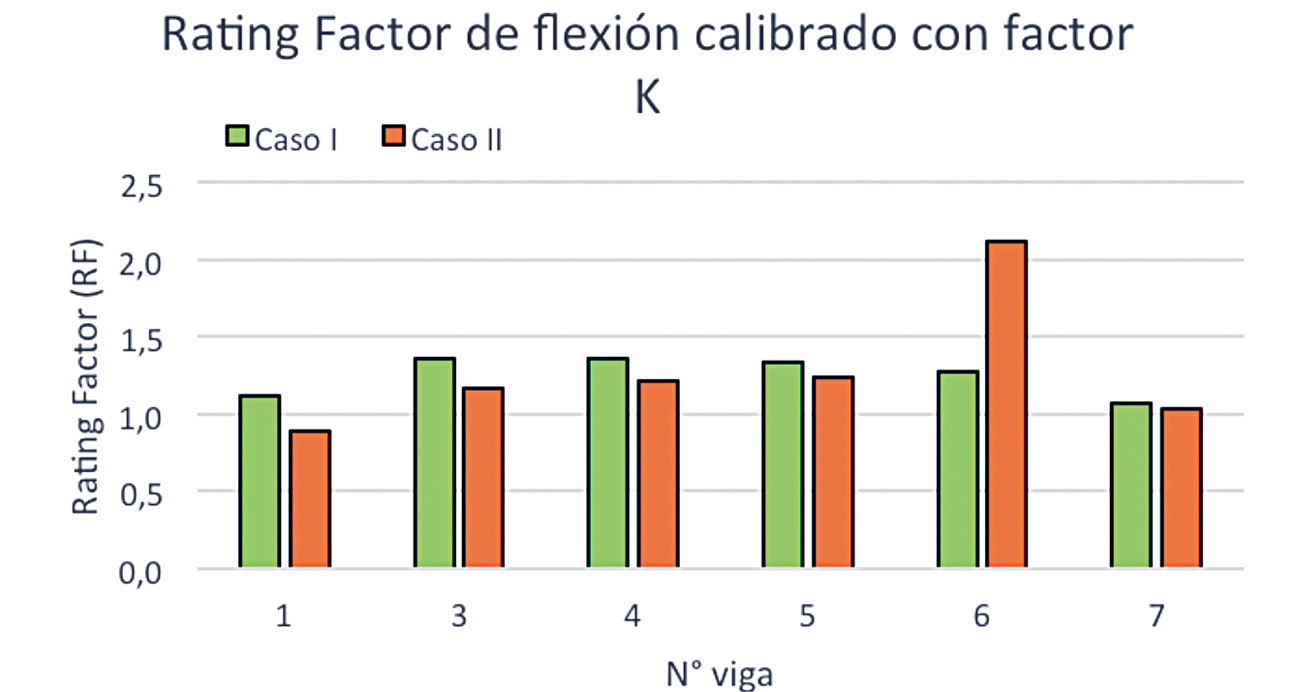
Figura 5. Rating Factor de flexión calibrado para prueba de carga de diagnóstico – Caso I y II.
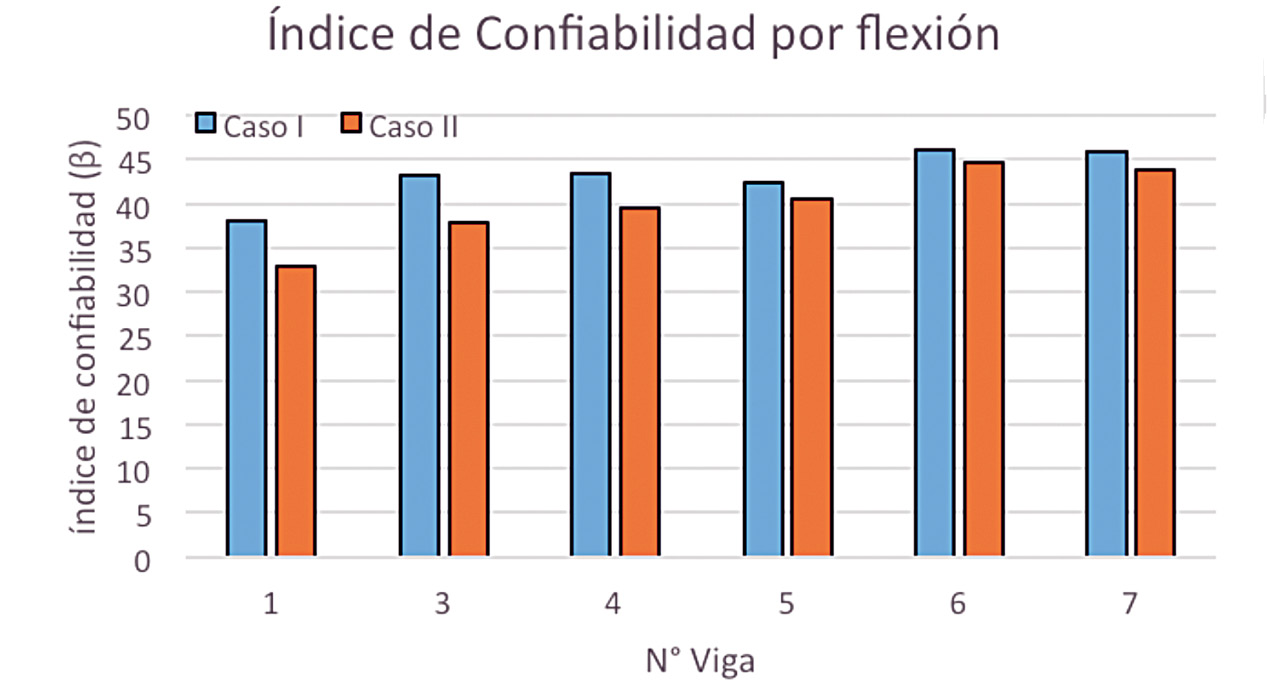
Figura 6. Índice de confiablidad por flexión para prueba de carga de diagnóstico – Caso I y II.
Otra diferencia destacable es la influencia que posee modelo teórico del puente en el RFP debido al factor K, lo que puede reducir significativamente el margen de seguridad calculado. Mientras que en el β no tiene importancia para su cálculo.
Conclusiones y recomendaciones
El método de capacidad de carga, es sumamente útil para la determinación de la resistencia y carga permisible; es adaptable a diferentes puentes, con factores prestablecidos por [14], pero puede llegar a ser conservador debido a que persigue un punto crítico de estado límite, por lo que puede no describir de la mejor manera el estado de seguridad estructural del puente. Se recomienda su uso preferiblemente para conocer si el puente soporta el paso de vehículos especiales, establecer un límite de peso de vehículos para pasar el puente o si se conoce con exactitud las cargas máximas que transitan el puente; ya que estos casos es preferible ser conservador.
En las limitaciones del método está el factor K, que tiene una influencia significativa por parte del modelo teórico del puente, por lo cual, si el modelo o la prueba de carga no son realizados correctamente, puede afectar el resultado final. Además, solo se puede evaluar un caso a la vez.
El índice de confiabilidad, permite evaluar el estado límite real de los elementos, a partir de la descripción estadística real de la carga y los parámetros de resistencia. Lo que resulta en un acercamiento más certero de la seguridad estructural del puente en estudio. Sin embargo, los resultados demuestran índices sobre calificados para una condición excelente, debido a que el puente en el caso de estudio tenía solo 1 año de construido. Por lo tanto, se recomienda el uso de este método para puentes envejecidos, donde se denote deterioro que comprometa la salud estructural del puente, o en puentes importantes para la red vial donde la cantidad y tipo de tránsito sea variable y su colapso comprometa el funcionamiento vial.
Las limitaciones esenciales de este método, radican en la obtención de los parámetros estadísticos reales de los materiales y su verdadera distribución de probabilidad, puesto que una distribución supuesta (como se hizo en este trabajo) puede inducir a errores para la distribución de probabilidad de la resistencia, que a su vez afecta la forma de cálculo del índice [ver 12].
La prueba de carga de diagnóstico, es una herramienta valiosa para la evaluación de la condición del puente, puesto que permite aplicar métodos más objetivos y desde un punto de vista estructural, lo que funciona para complementar la metodología actual de Costa Rica. Además de poder calibrar los modelos teóricos computacionales del puente, para tener un mejor comprensión del comportamiento ante las cargas y futuros análisis.
Agradecimientos
Agradezco a la Ing. Giannina Ortiz Quesada por el apoyo y experiencia compartida para llevar a cabo este proyecto.
Referencias
[1] Ministerio de Obras Públicas y Transportes (MOPT). Manual de Inspección de Puentes. San José, Costa Rica, 2007.
[2] J. Muñoz, P. Agüero, S. Vargas, E. Villalobos, L. Vargas, R. Barrantes y G. Loría. Guía para la determinación de la condición de puentes en Costa Rica mediante inspección visual. San José, Costa Rica, 2015.
[3] M. Sanayei, A. Reiff, B. Brenner y G. Imbaro. Load Rating of a Fully Instrumented Bridge: Comparison of LRFR Approaches. Journal of Performance of Constructed Facilities, ASCE, pp. 04015019-1 – 04015019-7, 2016.
[4] F. Picado y G. Ortiz. Desarrollo de un modelo de confiabilidad para el análisis del desempeño de puentes. Un caso de estudio en Costa Rica. Tecnología en Marcha. Costa Rica. Volumen 30–1, pp. 79 – 89, 2017.
[5] Y. Chen y P. Agüero. Introducción al monitoreo de la condición estructural de puentes. Programa de Ingeniería Estructural. Costa Rica. Volumen 2 N°5, 2017
[6] Centro de Investigación en Vivienda y Construcción (CIVCO). Informe de resultados de prueba de carga de diagnóstico en puente sobre Río Peje, Siquirres. Propiedad de Instituto Costarricense de Electricidad. Cartago, Costa Rica, 2017.
[7] A. Estes y D. Frangopol. Load Rating versus Reliability Analysis. Journal Structures Engineering, ASCE, pp. 843 – 847, 2005.
[8] D. Frangopol y J. Kong. Life-Cycle Safety and Costing For Maintenance of Aging Bridges. Journal Structures, ASCE, pp. 1 – 6, 2001.
[9] D. Frangopol y D. Saydam. Performance Indicators for Structures and Infrastructures. Structures Congress 2011, ASCE, pp. 1215 – 1226, 2011.
[10] D. Frangopol, A. Strauss, y S. Kim. Bridge Reliability Assessment Based on Monitoring. Journal of Bridge Engineering, ASCE, pp. 258 – 270, 2008.
[11] L. Gao. Reliability-based Evaluation of Bridges Live Load Carrying Capacity in the United States. Washington, Estados Unidos, 2012.
[12] S. Hooman. Target Reliability Analysis for Structures. Thesis. Graduate Faculty, Auburn University, 2015.
[13] X. Xiao, Z. Hu y T. Jinhua. Reliability Simulation and Sensitibity Analysis of Prestressed Concrete Bridge. CICTP 2014: Safe, Smart and Sustainable Multimodal Transportation Systems, ASCE, pp. 2036 – 2041, 2014.
[14] American Association of State Highway and Transportation Officials (AASHTO). The Manual for Bridge Evaluation. 2da ed. Estados Unidos. Editorial: American Association of State Highway and Transportation Officials, 2011.
[15] C. Cai, y M. Shahawy. Understanding Capacity Rating of Bridges from Load Tests. Journal Practice Periodical on Structural Design and Construction, ASCE, pp. 209 – 216, 2003.
[16] Ingenio xyz. Retos de rigidez - ¿Cuál es el camino de las cargas? [https://www.youtube.com/watch?v=BvcmOmmpCdo], Setiembre, 2017. (accesado: 21 Agosto, 2018).
1 Ingeniero en Construcción, Instituto Tecnológico de Costa Rica. Cartago, Costa Rica. Correo electrónico: darnelb19@gmail.com.  https://orcid.org/0000-0003-4050-7482
https://orcid.org/0000-0003-4050-7482
2 Sistema de Administración de Puentes.