Optimización de Recursos mediante la Simulación de Eventos Discretos

Optimization of Resources through Simulation of Discrete Events

Erik Orozco-Crespo1, Neyfe Sablón-Cossio2, Ramiro Saraguro-Piarpuezán3, Dalila Hermoso4, Yadamys Rodríguez-Sánchez5

Fecha de recepción: 21 de junio de 2018
Fecha de aprobación: 19 de setiembre de 2018

Orozco-Crespo, E; Sablón-Cossio, N; Saraguro-Piarpuezán, R; Hermoso, D; Rodríguez-Sánchez, Y. Optimización de Recursos mediante la Simulación de Eventos Discretos. Tecnología en Marcha. Vol. 32-2. Abril-Junio 2019. Pág 146-164.

DOI: https://doi.org/10.18845/tm.v32i2.4356

Palabras clave

Optimización; simulación de eventos discretos; asignación de recursos.

Resumen

Gran parte del éxito de una organización se concentra en la toma de decisiones en su función de operaciones. Administrar adecuadamente los recursos que intervienen en sus procesos de transformación, se convierte en un verdadero reto en aras de elevar la efectividad. Ante lo cual, aparece la optimización, basada en la simulación de eventos discretos, como herramienta de gran potencial en los sistemas productivos o de servicios, no sólo por los ahorros que implica su uso en cuanto a tiempo y costo, sino también por su potencial para minimizar errores en la toma de decisiones. En correspondencia con lo anterior, el presente trabajo se propuso demostrar (Objetivo) las fortalezas de estas herramientas como soporte a la toma de decisiones, que optimicen la asignación de hombres y máquinas en procesos productivos con cierto nivel de complejidad y que garanticen el mínimo costo total, el cumplimiento de los planes de producción y un buen desempeño del sistema. Para ello, se aplicaron los softwares FlexSim, como simulador de eventos discretos, de conjunto con sus herramientas Experfit y Experimenter; y el IBM SPSS Statistics para otros análisis estadísticos. Los resultados son presentados con la aplicación a un caso de estudio relacionado con una empresa productora de medias y perteneciente al sector textil en la provincia Imbabura, Ecuador; al lograr asignar los recursos disponibles por cada una de las subsecciones y secciones de trabajo pertenecientes al punto limitante del proceso productivo y ajustadas a las cantidades determinadas en el Plan Maestro de Producción. Lo anterior, garantizando un mínimo de costo total en el cumplimiento de dicho plan y un buen desempeño de las principales métricas en la operación.

Keywords

Optimization; simulation of discrete events; resource allocation.

Abstract

Much of the success of an organization is focused on making decisions in its function of operations. Managing appropriately the resources that intervene in their processes of transformation, becomes a real challenge in order to increase effectiveness. For this, Optimization, based on the simulation of discrete events, appears as a tool with great potential in the productive or service systems, not only for the savings implied by their use in terms of time and cost, but also for its potential to minimize errors in making of decisions. In correspondence with the above, the present work set out to demonstrate (Objective) the strengths of these tools as support for decision-making, which optimize the assigment of men and machines in productive processes with a certain level of complexity and that guarantee the minimum total cost, the fulfillment of the production plans and a good performance of the system. FlexSim software was applied as simulator of discrete events, together with its Experfit and Experimenter tools. The IBM SPSS software was applied for other statistical analyzes. The results are presented with the application to a case study related to a company producing socks and belonging to the textile sector of Imbabura province, Ecuador. The men and machines assignment is made by each of the sections and subsections that make up the limiting point of the production process, adjusted to the amounts determined in the Master Production Schedule for each type of socks, ensuring minimal total cost and good performance of the principal metrics in that operation.

Introducción

La toma de decisiones en el diseño de productos y procesos avanza notablemente en las últimas décadas debido a los avances en el área de la informática, las nuevas formas de producción (tecnología 3D) y la elaboración de materiales alternativos. Específicamente, la simulación de estos sistemas recibe considerables avances a partir del desarrollo de lenguajes de programación y software comerciales, que permiten que sea una de las técnicas más empleadas en la Investigación de Operaciones y Ciencias de la Administración.

Una de las áreas de aplicación más amplias de la simulación son los sistemas de producción, entre otras razones, porque la simulación demuestra ser útil en la estimación de un nuevo diseño del sistema [1]. Se constituye en una herramienta importante de análisis dinámico para apoyar las decisiones de programación, secuenciación, cargas de trabajo, planeación de la capacidad y predicción de los tiempos de entrega, a diferencia de muchas otras, no considera los tiempos de ciclo como constantes [2]. A este entorno se relaciona el presente caso de estudio, perteneciente al sector textil de la provincia Imbabura en el Ecuador. Esta fábrica productora de medias o calcetines, produce para este mercado desde hace más de 20 años y es considerada la segunda más grande del país en cuanto a su capacidad de producción. Su proceso productivo se clasificó como un sistema de flujo en lotes, que oscilan entre los medianos y grandes según la nomenclatura de productos. Las órdenes de los clientes se satisfacen desde los inventarios siendo un sistema make to stock [3].

Este sistema se compone de cinco operaciones: formado, cosido, virado, planchado y etiquetado. De ellas, el formado o tejido de la media resultó ser la operación punto fundamental y cuello de botella. Está compuesta por 212 máquinas automatizadas que agregan el mayor valor al producto y laboran bajo condiciones de alta continuidad, con un régimen laboral de 24 horas al día, de lunes a sábado y en dos turnos de trabajo durante el día y la noche. Las marcas de estas máquinas son Lonati, Sangiacomo y Conti y están agrupadas en cinco secciones en correspondencia con tres generadores de aire comprimido. Este layout permite, como principal objetivo, no producir grandes variaciones en el factor de potencia durante la semana, disminuyendo así los gastos por concepto de energía, y a su vez, el costo de producción. A la par, la asignación de la cantidad de ellas a emplear durante la semana de trabajo se realiza de acuerdo a las cantidades determinadas en el Plan Maestro de Producción y según el surtido de medias que se van a producir. En cuanto se refiere al talento humano, este es asignado por subsecciones y se compone de enebradores y viradores. Entre otras actividades, los primeros se dedican a atender los paros de las máquinas y los segundos a virar las medias y manipularlas hasta el área de producción en proceso.

A este panorama se dirigió la modelación en Flexsim6 de esta operación, con la finalidad de ajustar la asignación de recursos hombres y máquinas a las cantidades de medias a producir y determinadas en el Plan Maestro de Producción, que garanticen el mínimo costo total y un buen desempeño del sistema. Para tales fines, este modelo toma como base el elaborado por Orozco Crespo & Hermoso Ayala (2017).

Como herramienta descriptiva de la Investigación de Operaciones, demuestra su utilidad en el proceso de análisis y diseño de sistemas complejos ante la necesidad de estudiarlos para aumentar la comprensión de las relaciones entre los diversos componentes, o para predecir el desempeño bajo nuevas condiciones de operación [4].

Aplicación en la producción de la simulación

En base al objeto de aplicación dentro del sistema de producción se definen las variables, problema a resolver y que simular en base a los contextos específicos. Ejemplo de ello, son sus aplicaciones en:

•La administración de los inventarios de [5, 6], los indicadores y modelos en relación a sus características [7, 8],

•el análisis y validación de las medidas de desempeño en los sistemas de manufactura de [9],

•las aplicaciones de mejoras mediante despliegues Seis Sigma de [10],

•En el método Kanban, como filosofía dentro del sistema de producción asociado al Just in Time [11], con la mayor expresión en la línea de ensamblaje Toyota [12]; donde la aplicación de las líneas de ensamblajes presenta un gran interés [13], .

•La capacidad como variable que limita el proceso de manufactura [14].

•La estimación de la demanda, y como entrada al sistema de producción para las decisiones en otros procesos [15], por ejemplo con la distribución y el inventario [16], con la suma de las decisiones de venta y su relación dentro del sistema de producción [17].

•En el diseño de plantillas, asignación de trabajadores a puestos de trabajo [18], y la secuencia óptima para el ajuste a la demanda [19].

•En localización de instalaciones [20], y su relación entre su distribución y capacidad (almacenes, vehículos, equipos de Mantenimiento, relaciones de clientes).

•En relación a la distribución tanto dentro como fuera del sistema de producción [21, 22].

•Las reglas de programación de la producción [23].

•En las teorías de las restricciones [24], y que ofrecen medidas de rendimiento.

Como herramienta descriptiva de la Investigación de Operaciones, demuestra su utilidad en el proceso de análisis y diseño de sistemas complejos ante la necesidad de estudiarlos para aumentar la comprensión de las relaciones entre los diversos componentes, o para predecir el desempeño bajo nuevas condiciones de operación [4]. En este caso de estudio se aplica la simulación a la asignación de hombres y máquinas en un sistema de producción que garanticen el mínimo costo total, el cumplimiento de los planes de producción y un buen desempeño del sistema.

Materiales y Métodos

Para el desarrollo del modelo se utiliza una aproximación a la metodología de simulación de seis pasos de Harrell [25], y de planificación de la producción de Domínguez [26]. Ambas se funden en un procedimiento que relaciona ambas metodologías (figura 1).

El objetivo de la simulación estuvo dirigido a la optimización, fundamentalmente, para que el modelo permitiera identificar posibles alternativas de solución para la asignación de los recursos hombres por subsección de trabajo y máquinas para la producción de los diferentes tipos de medias, que cumplan satisfactoriamente con el Plan Maestro de Producción (PMP), que garanticen el mínimo costo total y un adecuado uso de estos recursos.

Se definieron las variables de decisión siguientes: cantidad de enebradores y viradores a utilizar ( y ); cantidades de máquinas para la producción de los diferentes tipos de medias (). Las combinaciones de estas variables de decisión generaron los posibles escenarios en los que fueron medidas las métricas de desempeño del modelo a partir de sus variables dependientes o de respuesta (cuadro 1).

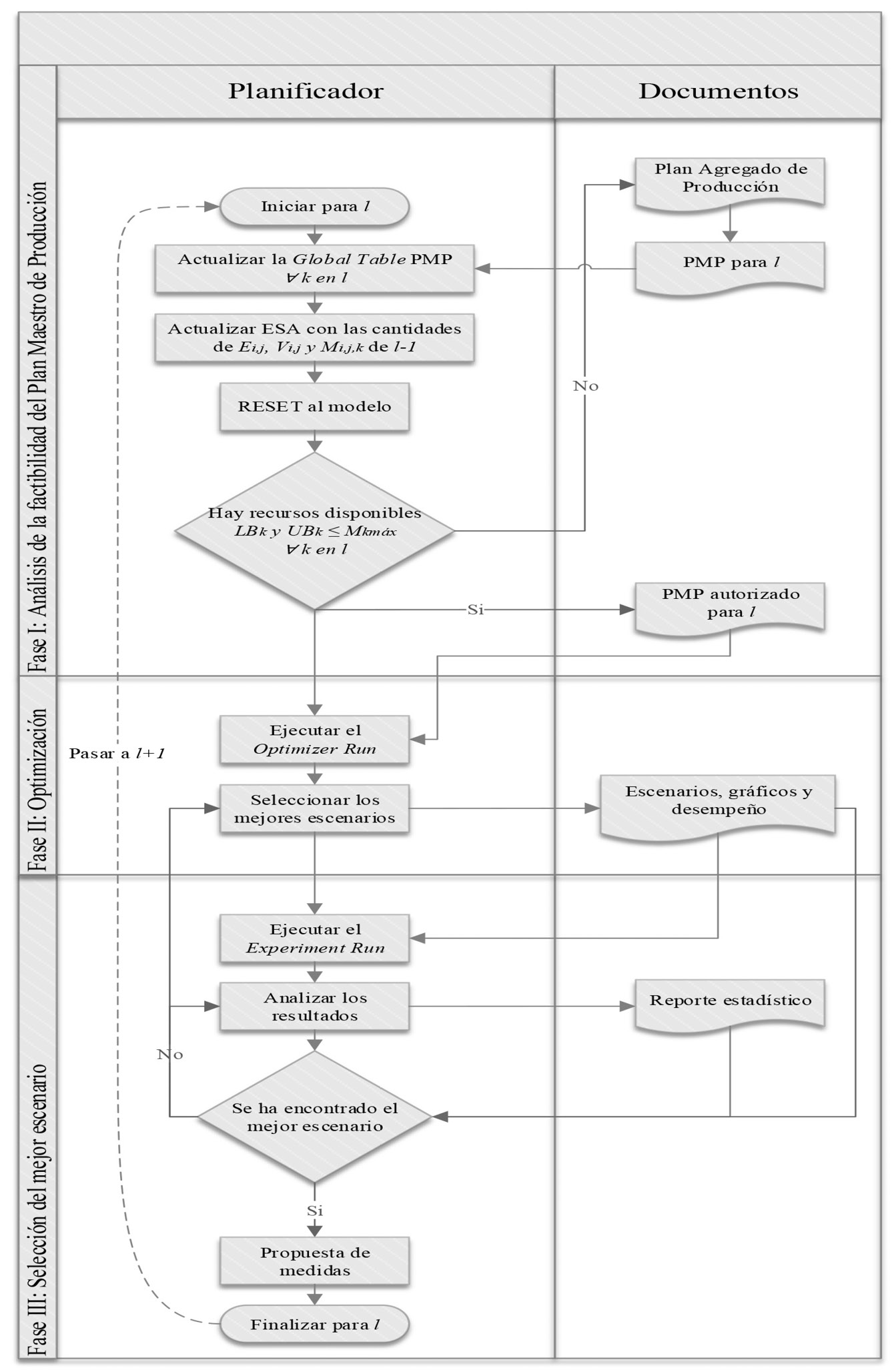
Figura 1. Diagrama de flujo para la lógica del modelo

Cuadro 1. Planteamiento de las variables de respuesta.

Objetivos específicos de la simulación	Variable dependiente	Denominación	UM
Determinar la utilización de los recursos, tanto de los trabajadores como de las máquinas	Promedio del porcentaje de utilización de los enebradores	UEi,j	(%)
	Promedio del porcentaje de utilización de los viradores	UVi,j	(%)
	Promedio del porcentaje de procesamiento de las máquinas	Pk	(%)
Analizar, de forma general, las causas que afectan el rendimiento en la operación, tanto las relacionadas con la maquinaria, como con la continuidad de desplazamiento de los items.	Promedio general del porcentaje de los paros de las máquinas (breakdowns)	B	(%)
	Promedio general del porcentaje de esperas de las máquinas por los enebradores para atender los paros	WOM	(%)
	Promedio general del porcentaje de esperas de los combiners por los viradores para el virado de la media	WO	(%)
	Promedio general del porcentaje de esperas por los viradores para el transporte al área final de producción en proceso	WT	(%)
Determinar el total de unidades producidas según su tipo	Total de docenas de medias producidas en la semana	Tk	(doc/sem)
	Rendimiento de la operación según el tipo de media	Rk	(doc/min)
Donde: i: secciones de trabajo (a, b, c, d y e) j: subsecciones en las que se dividen algunas de las secciones de trabajo (1 y 2) k: tipo de media (1, 2, 3, … y 21)

La concepción del modelo siguió la lógica que se muestra en la figura 1 y que consta de un conjunto de fases que se encuentran estrechamente relacionadas con su programación. La primera fase estuvo dirigida al análisis a grosso modo de la factibilidad del PMP, para determinar si existe capacidad suficiente para enfrentar el volumen de producción que plantea el plan para cada uno de los ítems en la semana que se planifica (l). Este proceso sigue una lógica similar a lo planteado en [27] para el proceso de elaboración de este plan y posee como principales insumos al Plan Agregado de Producción y al PMP. De no existir disponibilidad de recursos para enfrentar el volumen de producción que se planifica habrá que hacer ajustes al Plan Agregado de Producción con previa consulta al resto de las áreas de la fábrica o, como última alternativa, reprogramar máquinas para aquellos ítems con déficit de capacidad, lo cual no forma parte del modelo ya que se asumió exceso de capacidad de la fábrica dadas las ventas de los últimos años. En caso contrario se obtiene el PMP autorizado sobre el cual funcionará el modelo y que constituye el insumo fundamental para la siguiente fase.

En la fase de Optimización lo más importante fue el análisis de las soluciones obtenidas por el Optimizer Run y la selección de las soluciones factibles que minimicen los costos totales y que posean altos niveles de cumplimiento del plan de producción. Posterior a este análisis, se exportó dicha selección, además, se salvaron en un documento Word los principales resultados gráficos y en un documento en Excel los resultados de todas las variables de respuesta y de la función objetivo. Todo ello con las opciones Export Selected Scenarios, Export Screenshot y Export as CSV del Optimizer Run.

Estos documentos fueron de gran utilidad para el desarrollo de la siguiente fase destinada a la Selección del mejor escenario. En ella se corrió el Experiment Run para el Escenario de la Semana Anterior (ESA) y los seleccionados en la Fase II para la semana actual. Posteriormente, se analizó el comportamiento de las variables de respuesta a partir de sus valores medios, desviaciones estándar e intervalos de confianza para un 95% de nivel de confianza. Se compararon los escenarios entre sí y respecto a ESA, hasta encontrar el mejor escenario para la semana que se planifica. Posterior a lo cual, se toman las medidas pertinentes referidas a los ajustes de máquinas necesarios, así como, las reubicaciones de los trabajadores en las subsecciones de trabajo de la operación u otras áreas productivas dentro de la fábrica. Como otro resultado de esta fase se obtuvo el reporte estadístico que se generó en el propio Experiment Run/View Results.

Resultados

Definir objetivos, alcance y requerimientos

El alcance del modelo de simulación comprendió la operación de formado de las medias, es decir, desde que el material (conos de hilo) ingresa a la operación, hasta que se almacenan las docenas de medias en las áreas de producción en proceso. Se consideraron 21 tipos de medias como las más representativas en cantidad y frecuencia de producción, de ellas las de algodón y poliéster según las tallas más demandadas y para no incrementar la complejidad en la programación del modelo.

Posterior a lo cual, se toman las medidas pertinentes referidas a los ajustes de máquinas necesarios, así como, las reubicaciones de los trabajadores en las subsecciones de trabajo de la operación u otras pareas productivas dentro de la fábrica. Como otro resultado de esta fase se obtuvo el reporte estadístico que se generó en el propio Experiment Run/View Results.

Recolectar y analizar los datos del sistema

Para el análisis de los paros de las máquinas se consultó a ocho expertos, que posterior a varias rondas, arrojaron como principales causas las que se muestran señaladas en el diagrama Ishikawa. La jerarquización de las causas de mayor incidencia sobre los paros de las máquinas se realizó mediante el vector B, obtenido al aplicar el método Analytic Hierarchy Process (AHP) de Saaty [28], cuadro 2.

Cuadro 2. Cálculo del vector B para la jerarquización de las causas.

Causas de paros en las máquinas		Vector B A*B	Vector C	Vector D
C1	Errores electrónicos	0,10	0,81	8,20
C2	Material de mala calidad	0,25	2,34	9,20
C3	Fallas mecánicas	0,15	1,36	9,10
C4	Desabastecimiento de MP	0,10	0,89	8,61
C5	Falta de planificación de mantenimiento	0,27	2,49	9,10
C6	Ineficiencia en el arreglo del paro	0,05	0,40	8,25
C7	Mala programación de la máquina	0,04	0,36	8,31
C8	Condiciones ambientales	0,03	0,23	8,15

Ordenadas de la manera siguiente:

•C5: Falta de planificación del mantenimiento, predominando el mantenimiento correctivo.

•C2: Material de mala calidad que origina partiduras de los hilos.

•C3: Fallas mecánicas que se deducen del desgaste mecánico de las piezas.

•C1: Errores electrónicos que se traducen en fallas eléctricas y de programación de las máquinas.

•C4: Desabastecimiento de materia prima (conos de hilo) a las máquinas de formado.

Se aceptaron los resultados al obtener una razón de inconsistencia en la opinión de los expertos de 0.06, menor a 0.10 [28]. A excepción de la C5, las cuatro causas restantes fueron estudiadas por separado en cuanto a su repercusión en la utilización de las máquinas para, posteriormente, ser introducidas al modelo de simulación en forma de downtimes.

Adicionalmente, se analizó la defectuosidad en la propia operación (variable DEF), tanto por turno (factor Turno), como por cada sección de trabajo (factor Grupo). Para este análisis se aplicó un ANOVA Tipo II con el procedimiento del Modelo Lineal General Univariante, con la finalidad de evaluar el efecto de conjunto (factor Grupo-Turno) e individual (factor Grupo y factor Turno) que tienen estos factores sobre la variable DEF.

Como resultado de este análisis se obtuvo que el factor Grupo-Turno explicó el 35.3% de la variabilidad total de DEF, mientras que el efecto individual de los factores Grupo y Turno explicaron el 31.6% y el 2.5% de la variabilidad total de la variable DEF. Estos resultados estuvieron acompañados de valores de sigma cercanos a cero, que conllevaron a rechazar la hipótesis nula de considerar como no significativos el efecto de estos factores; y concluir que los grupos de máquinas fueron los que más incidieron en que los valores medios de DEF fueran diferentes (cuadro 3).

Cuadro 3. Resumen del ANOVA Tipo II.

Factor	F	Sig.	Eta al cuadrado parcial	R cuadrado corregida
Factor Grupo-Turno	30.753	0.00	0.365	0.353
Factor Grupo	56.437	0.00	0.322	0.316
Factor Turno	16.664	0.00	0.027	0.025

Se concentraron las mayores diferencias de DEF, medidas por turno y por grupo de máquinas, se realizó un análisis Post-Hoc con los estadísticos T3 de Dunnett y Games-Howell, debido a la inexistencia de homocedasticidad. Estos resultados se resumen en el gráfico de medias marginales de la figura 2.

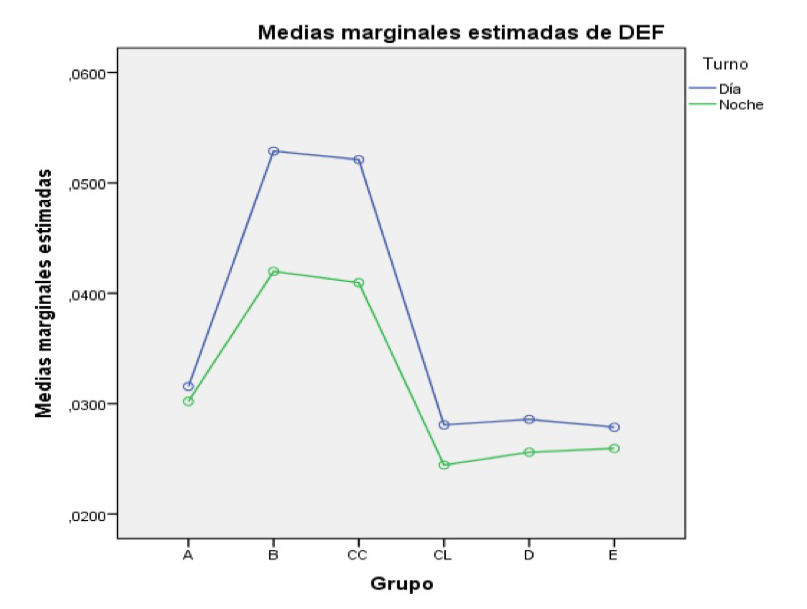
Figura 2. Medias marginales de DEF por grupo y por turno.

Como resultado de esta prueba se concluyó que existió igualdad de medias entre las defectuosidades originadas por los grupos de máquinas b y cc; entre cl, d y e; y que el grupo de máquinas a arrojó defectuosidades diferentes al del resto de los grupos. A partir de lo cual, se decidió entrar al modelo de simulación la defectuosidad promedio medida por secciones de máquinas, sin hacer distinción entre los turnos de trabajo. A la par, se entraron valores de defectuosidad iguales para los grupos de máquinas b y cc; cl, d y e; y diferentes para el grupo de máquinas a.

La recolección de los datos se dividió en dos categorías: estructurales y numéricos. Los primeros definieron los elementos del sistema, tales como: máquinas, cajas para la producción en proceso, los trabajadores y el layout de la fábrica.Los segundos se relacionaron con la toma de datos y análisis estadístico mediante el empleo de la herramienta Experfit, cuyos resultados se muestran en los cuadros 4 y 5.

Cuadro 4. Resumen del Goodness of Fit Anderson-Darling para los tiempos de formado de las docenas.

Análisis de Hipótesis
Operación	Sección	Variable	Modelo	Test Static	Critical Value	Reject
Formado	D y E (Marca LONATI)	Tiempo de formar una docena	Weibull (133.66, 16.45, 8.86)	0.41	2.492	No
	C y A (Marca CONTI); B (Marca SANGIACOMO)	Tiempo de formar una docena	Johnsonbounded (36.74, 79.65, -0.37, 0.76)	0.38	2.492	No
	C (Marca LONATI)	Tiempo de formar una docena	Beta (45.29, 202.57, 7.93, 2.35)	0.39	2.492	No

Resultaron constantes para el modelo: los tiempos de formado de las medias, la velocidad de movimiento de los trabajadores, los tiempos de cargas y descargas de los trabajadores en la manipulación interna de las docenas de medias y los tiempos para el almuerzo, merienda y cambios de turno asociados al régimen laboral, cuadro 5.

Para la construcción del modelo se añadieron: sources, processors, queues, combiners, sinks, task executers y dispatchers, que resultaron en la vista superior de la operación (figura 3); así como, funcionalidades para los breakdowns, task sequences, ruteos y el régimen laboral mediante time tables.

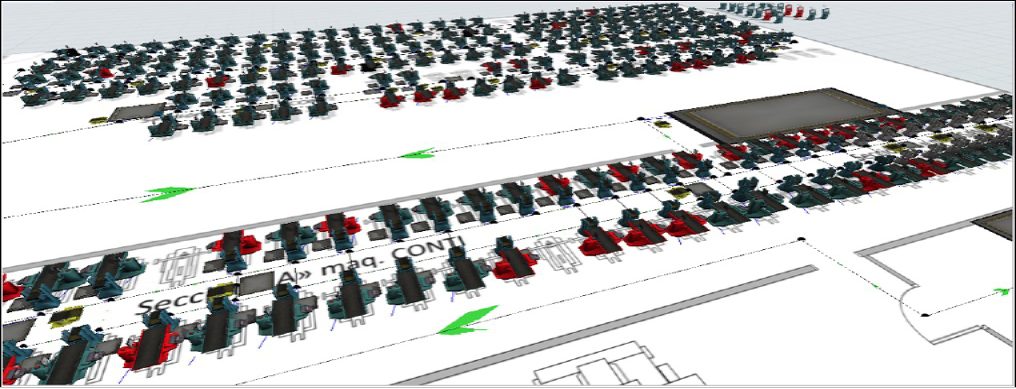
Figura 3. Vista superior del modelo en la operación de formado de la media.

Posterior a la construcción de los elementos básicos anteriores, fueron añadidas funcionalidades que siguieron la lógica del diagrama de flujo de la figura 1 y que comienza con la actualización de datos en la Global Table denominada PMP. Esta Global Table se diseñó para disminuir el rango de búsqueda de soluciones para la cantidad de máquinas totales a asignar para la producción de los distintos tipos de medias y para contribuir con la rapidez en la obtención de los resultados en la optimización (figura 4).

Cuadro 5. Resumen del Goodness of Fit Anderson-Darling para los tiempos de paros de las máquinas.

Análisis de Hipótesis
Operación	Sección	Tipo de Down Time	Time	Modelo	Test Static	Critical Value	Reject
Formado	D y E (Marca LONATI)	Errores de máquina	Up Time	weibull(513.97, 923.12, 1.76)	0.25	2.492	NO
			Down Time	Johnsonbounded(0.33, 10.27, -0.62, 1.61)	0.21	2.492	NO
		Paros que dañan la media	Up Time	Beta(4.37, 43288.86, 1.48, 2.31)	0.25	2.492	NO
			Down Time	Peatsont5(153.94, 2582.13, 14.82)	0.81	2.492	NO
		Paro por rotura de hilos	Up Time	Beta(14.50, 31689.08, 1.55, 1.91)	0.31	2.492	NO
			Down Time	Johnsonbounded(11.38, 14.38, -0.44, 1.08)	0.36	2.492	NO
		Paro por desabastecimiento de M.P.	Up Time	Johnsonbounded(1270.23, 40226.61, -0.92, 1.21)	0.26	2.492	NO
			Down Time	Weibull(13.04, 170.86, 4.10)	0.32	2.492	NO
	C y A (Marca CONTI); B (Marca SANGIACOMO)	Errores de máquina	Up Time	Beta(288.14, 1963.70, 1.78, 1.40)	0.16	2.492	NO
			Down Time	Johnsonbounded(4.21, 8.25, -0.58, 1.50)	0.21	2.492	NO
		Paros que dañan la media	Up Time	Johnsonbounded(2354.62, 18940.93, 1.82, 0.88)	0.54	2.492	NO
			Down Time	Johnsonbounded(352.41, 418.23, -0.04, 0.53)	0.68	2.492	NO
		Paro por rotura de hilos	Up Time	Beta(553.39, 7878.21, 0.93, 2.34)	0.18	2.492	NO
			Down Time	Johnsonbounded(3.40, 22.92, -0.14, 1.15)	0.19	2.492	NO
		Paro por desabastecimiento de M.P.	Up Time	Beta(11798.50, 19917.07, 1.40, 1.06)	0.15	2.492	NO
			Down Time	Lognormal2(25.46, 10.18, 0.78)	0.28	2.492	NO
	C (Marca LONATI)	Errores de máquina	Up Time	Beta(46.44, 2990.23, 2.93, 2.84)	0.29	2.492	NO
			Down Time	Beta(3.65, 8.25, 5.05, 3.89)	0.23	2.492	NO
		Paros que dañan la media	Up Time	Weibull(0.00, 15253.32, 1.77)	0.26	2.492	NO
			Down Time	Johnsonbounded(203.97, 300.95, 0.41, 0.55)	0.34	2.492	NO
		Paro por rotura de hilos	Up Time	Weibull(1728.23, 16084.81, 2.00)	0.29	2.492	NO
			Down Time	Beta(10.36, 14.09, 5.69, 2.55)	0.28	2.492	NO
		Paro por desabastecimiento de M.P.	Up Time	Johnsonbounded(1971.59, 37938.52, -0.69, 1.38)	0.23	2.492	NO
			Down Time	Beta(27.45, 146.10, 0.65, 4.82)	0.15	2.492	NO

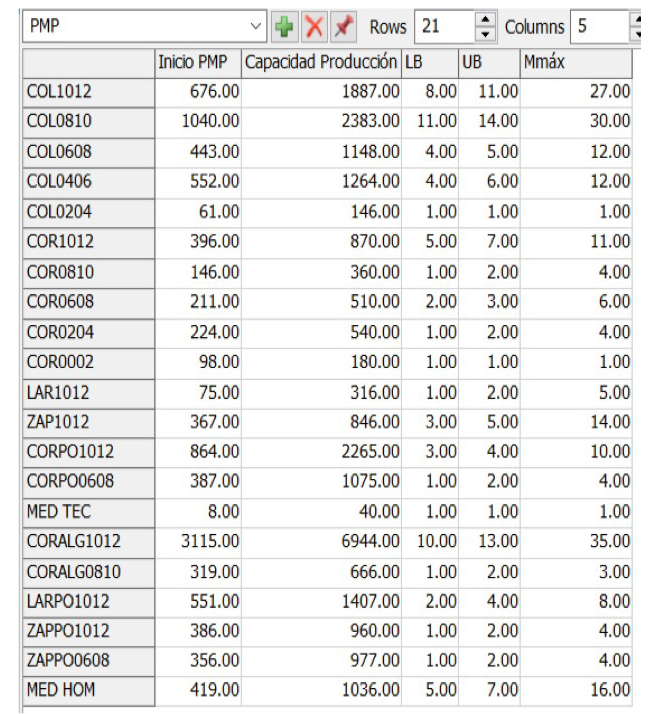
Figura 4. Global Table PMP.

La primera columna se introduce manualmente por el planificador de la producción sobre la base del PMP y antes de comenzar la semana de trabajo, medida en docena/semana. La segunda se corresponde con la capacidad de producción máxima efectiva de la operación obtenida en Orozco Crespo and Hermoso Ayala [29] y medida en docena/semana. La tercera y cuarta columnas son límites dentro de los cuales el software buscará la cantidad óptima del número de máquinas a asignar (Lower Bound y Upper Bound). El Lower Bound se calcula como si la operación fuese a funcionar a una eficiencia del 100% y el Upper Bound para una eficiencia del 85%, dadas las características de alta continuidad de la operación. La quinta columna es la cantidad de máquinas que, como máximo, pueden ser empleadas para la producción de un tipo de media y se corresponde con las que actualmente se encuentran programadas para tales fines según el Plan Agregado de Producción. Al dar RESET al modelo, se actualizan automáticamente los valores de Lower Bound y Upper Bound de las columnas tercera y cuarta.

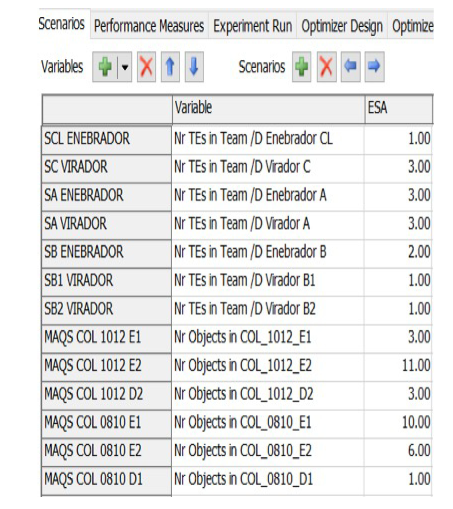
Figura 5. Escenario de la Semana Anterior (resumido).

Seguidamente, se actualizan las cantidades de recursos que realmente fueron empleados en ESA, es decir, los valores que tomaron las variables de decisión en la anterior semana y que pudieron resultar de procesos de optimización anteriores o de decisiones ajustadas por parte de operaciones. Esto se realiza en el Experimenter/Scenarios en la columna ESA (figura 7). Esto permitió comparar entre sí a los nuevos escenarios y a su vez compararlos con ESA al correr el Experiment Run. Además, de detectar los ajustes de máquinas necesarios, así como, las reubicaciones de los trabajadores en las subsecciones de trabajo de la operación u otras pareas productivas dentro de la fábrica.

Dentro del Experimenter, específicamente en el Star of Experiment, se programó otra funcionalidad que tuvo como principal fin el de seleccionar los valores totales de máquinas calculados en la Global Table PMP, tanto para el Lower como para Upper Bound, que se subdividen por cada una de las subsecciones de trabajo, sobre la base de la proporción real en la fábrica (figura 4) y establecerlos como el Lower y Upper Bound de estas variables en el Optimizer Design (figura 5). Al comenzar el proceso de experimentación estos valores se establecen automáticamente en las celdas anteriormente señaladas.

Fueron programadas disímiles variables en el Performance Measures, algunas dirigidas a determinar: los costos de almacenamiento, de materias primas y materiales, de ajuste de los equipos, de salario, de consumo de energía y otros costos que conformarán la función objetivo. Se añadió, otra variable dirigida a evaluar el cumplimiento del plan de producción y que formó parte de una de las restricciones del modelo. Se obvia la programación de las mismas en aras de ganar en brevedad.

La cantidad de trabajadores en el Lower Bound se definió como uno para todas las subsecciones de trabajo y en el Upper Bound se determinó en [30], y que se corresponde con la cantidad óptima de trabajadores a distribuir por las diferentes subsecciones para lograr la capacidad máxima efectiva de producción. Se planteó como restricción al modelo que el cumplimiento del plan de producción CP (%), es decir, que las cantidades entradas en la Global Table PMP como Inicio del PMP (docena/semana), se cumplan por encima del 95%, según los objetivos de la fábrica. Este valor dio la posibilidad de visualizar como soluciones factibles a todas aquellas que cumplieron con dicha restricción, aun cuando la selección de los mejores escenarios siempre estuvo asociada a las soluciones que arrojaron los costos totales mínimos y los mayores valores de CP. Se definió como función objetivo la que sigue:

Minimizar

CTe = CFe + CAe + CLe

Donde:

CTe: costo total de la alternativa o escenario e ($/semana).

CFe: costos asociados a la fabricación ($/semana) y que incluyó los gastos por concepto de materias primas y materiales (CMPMe), salario de los trabajadores (CSe), consumo de energía de las máquinas (CEe) y otros costos fijos como fueron los de depreciación de la maquinaria (COe).

CAe: costos aproximado para la producción en proceso ($/semana).

CLe: costo de ajuste de las máquinas ($/semana).

El Optimizer Run se corrió para 442 800 segundos, es decir, una semana de trabajo acorde con el régimen laboral y para un máximo de 100 soluciones a ser evaluadas.

Resultados del análisis de la factibilidad del PMP

En los resultados fueron seleccionadas la última semana del mes de mayo y la siguiente primera del mes de junio de 2017, que fueron consideradas como ESA (l-1) y como semana que se planifica (l), respectivamente. Las cantidades correspondientes al PMP para ambas semanas se muestran en el cuadro 6.

Esta selección respondió, por un lado, a que ambas semanas pertenecen a meses diferentes planificados en el Plan Agregado de Producción, y por otro, a la disminución de las cantidades de docenas a producir para todos los ítems. Esta última razón infirió desde un inicio la disminución de recursos totales a emplear para el cumplimiento del plan.

Cuadro 6. Cantidades planificadas en el PMP

k	Inicio del PMP (docenas)
	l-1 (ESA)	l
1	1089	676
2	1352	1040
3	483	443
4	721	552
5	100	61
6	566	396
7	194	146
8	259	211
9	327	224
10	96	98
11	198	75
12	514	367
13	1095	864
14	684	387
15	21	8
16	4164	3115
17	393	319
18	997	551
19	620	386
20	587	356
21	453	419

De análisis de factibilidad del PMP se obtuvo que las cantidades a producir en l son menores que la capacidad máxima efectiva de la operación para cada uno de los tipos de ítems (figura 6). A lo anterior se añadió que las cantidades de máquinas determinadas en el Lower y Upper Bound fueron menores o iguales a la cantidad máxima de máquinas que están programadas según el Plan Agregado de Producción. Dados estos resultados se obtuvo un Plan Maestro factible y que constituyó el insumo principal para el resto de los análisis.

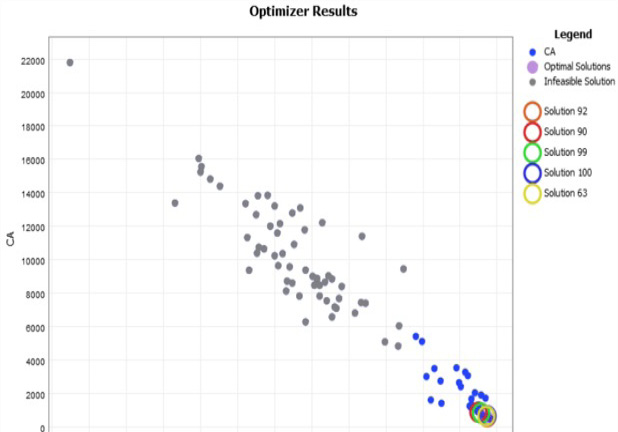
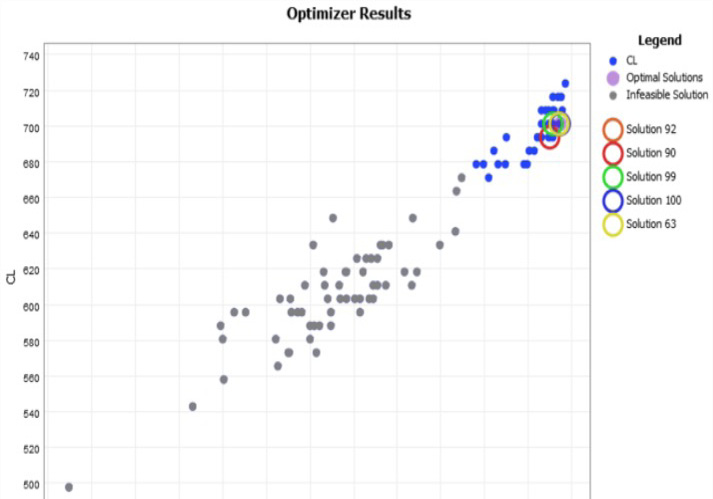
Figura 6. Resultados gráficos del Optimizer Run.

Resultados de la optimización

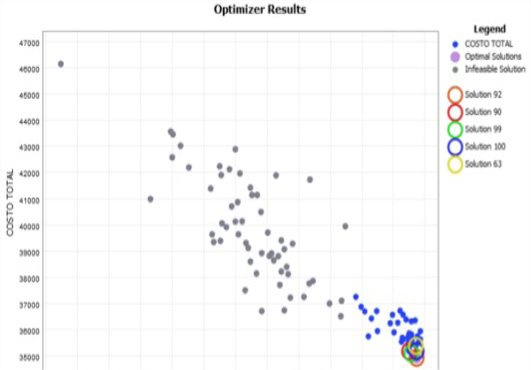
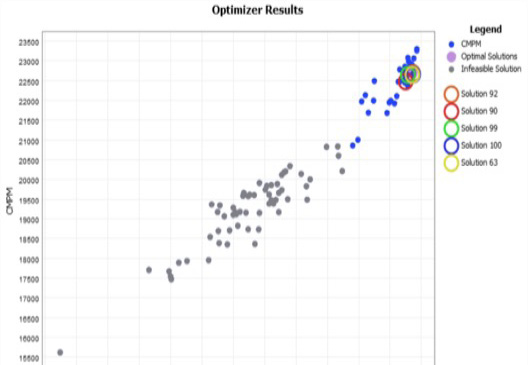
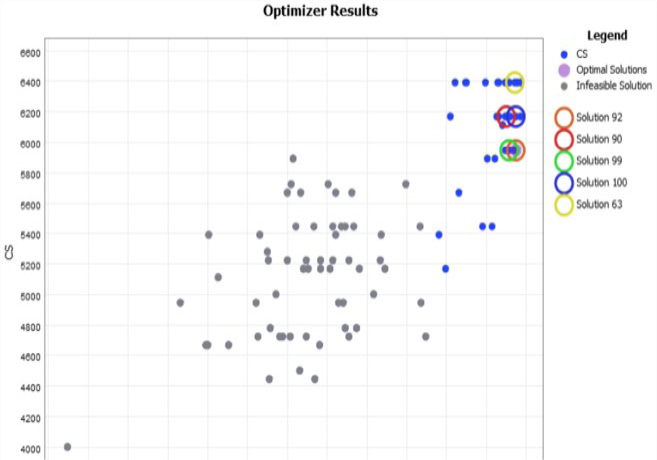
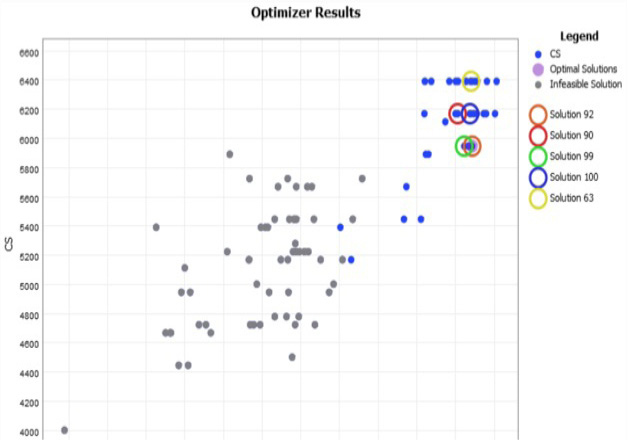
El comportamiento de los costos, el cumplimiento del plan y el rendimiento de los escenarios que fueron evaluados por el Experimenter se describen en la figura 12. Se seleccionaron las soluciones 92, 90, 99, 100 y la 63 porque minimizaron el CT y garantizaron valores de CP por encima del 95% (cuadro 7).

Cuadro 7. Resumen de los resultados de costos para los escenarios seleccionados.

Solución	CT ($)	CP (%)	CMPM ($)	CS ($)	CE ($)	CO ($)	CA ($)	CL ($)	R (doc/min)
ESA	44372.54	98.76	29949.96	5946.58	3738.66	2330.5	1434.184	972.66	2.00
92	34941.52	99.48	22680.56	5946.58	2689.98	2330.50	592.68	701.22	1.52
99	35114.73	99.14	22636.64	5946.58	2689.98	2330.50	809.81	701.22	1.51
90	35192.44	99.00	22471.44	6168.88	2659.94	2330.50	868.00	693.68	1.50
100	35192.55	99.48	22642.92	6168.88	2689.98	2330.50	659.05	701.22	1.52
63	35394.92	99.43	22640.54	6391.18	2689.98	2330.50	641.50	701.22	1.52

Estas soluciones disminuyeron sus costos respecto a ESA, lo cual se debió a la disminución de las cantidades a producir. Entre ellas obtuvieron similares resultados en cuanto a CMPM, CE y CO ya que produjeron similares cantidades de docenas en el período por lo que gastaron de similar manera en materias primas y materiales, emplearon aproximadamente la misma cantidad de equipos y depreciaron lo mismo. Además, obtuvieron niveles de CP por encima del 99% y similares niveles de rendimiento.

Los costos que determinaron la diferencia fueron el CS y el CA. Las soluciones 92 y 99 emplearon menor cantidad de trabajadores para poder cumplir con el plan, mientras que la solución 63 fue la que necesitó mayor cantidad de estos. Estas diferencias no repercutieron considerablemente en el rendimiento de la operación. La solución 92 resultó ser la de menor costo de almacenamiento ya que logró equilibrar mejor los costos de inventario y de pérdida de ventas producto del exceso o déficit de los mismos, respectivamente; no siendo el caso de las soluciones 90 y 99 que obtuvieron los peores resultados en este sentido debido a sus más bajos niveles de cumplimiento del plan de producción. Sobresalieron como mejores candidatas las soluciones que siguen:

•La solución 92 con un mínimo CT de $ 34941.52 y con el mayor nivel de CP de 99.48%.

•La solución 90 como tercera mejor respecto a CT. Aun cuando esta solución obtuvo el menor valor de CP con un 99%, resultó ser la de menor CL de todas las soluciones; y, por ende, fue la que garantizó mayor facilidad de trabajo, es decir, menos ajustes de máquinas respecto a ESA.

•La solución 100 como tercera mejor respecto a CT y con igual nivel de CP que la solución 92.

Quedaron descartadas las soluciones 99 porque en cuanto a CT resultó ser similar a la solución 92 pero con menor valor de CP; y la solución 63 debido a que fue la de peor resultado en cuanto a CT, influenciado por tener mayor CS.

Las soluciones seleccionadas indicaron la misma cantidad de trabajadores totales respecto ESA, a partir de lo que se infirió una disminución en la utilización de estos recursos si se tiene en cuenta que disminuyeron las cantidades declaradas en los PMP de una semana a otra. La cantidad de enebradores fue la misma para todas las combinaciones de (i,j), mientras que los viradores variaron para (d,1) y (c,1). Además, disminuyeron las cantidades totales de equipos a emplear respecto a ESA, lo cual es lógico al disminuir las cantidades las cantidades a producir. En tal sentido sobresalieron Me,2,1 , Mc,2,12 , Ma,2,16 y Mb,1,18.

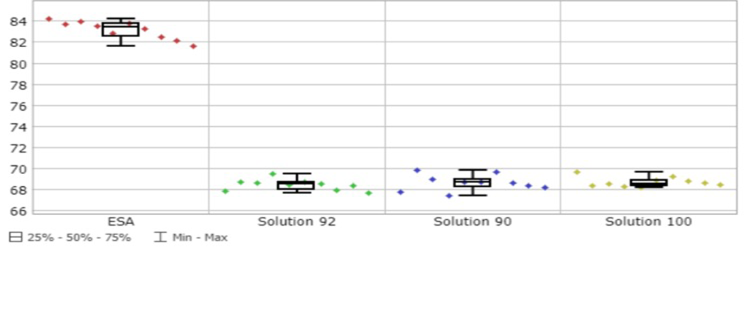
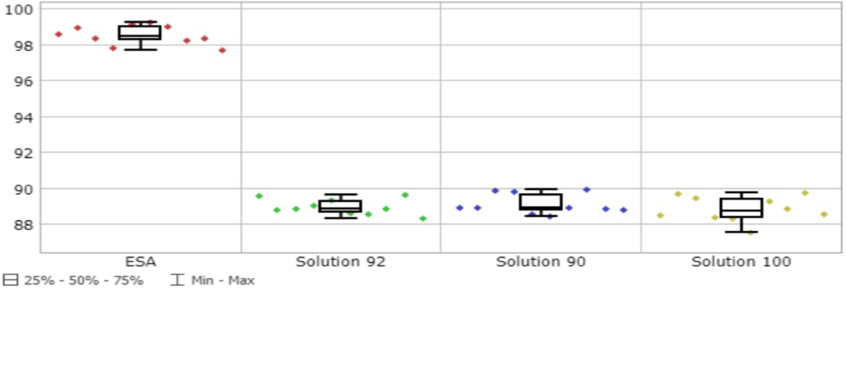
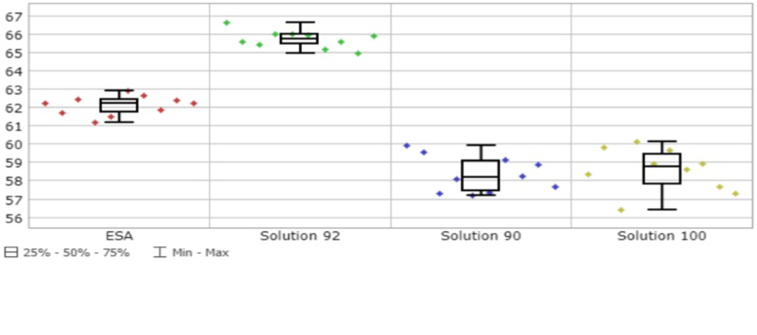
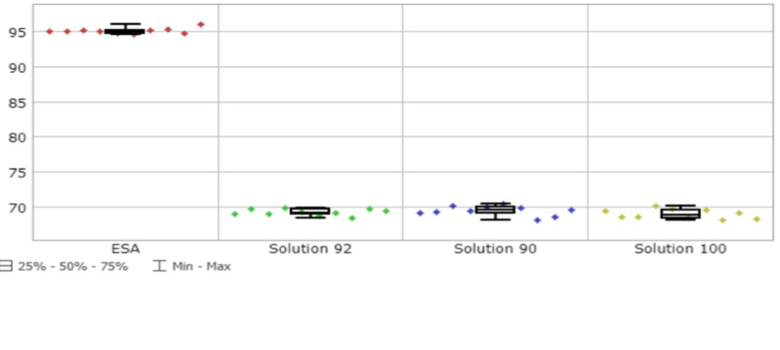
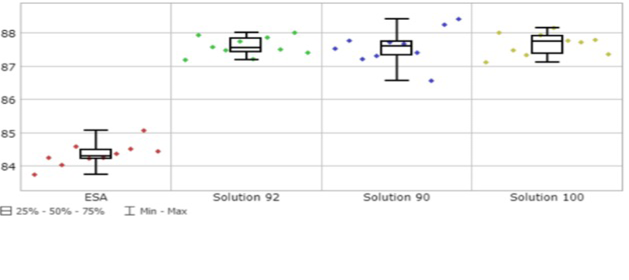
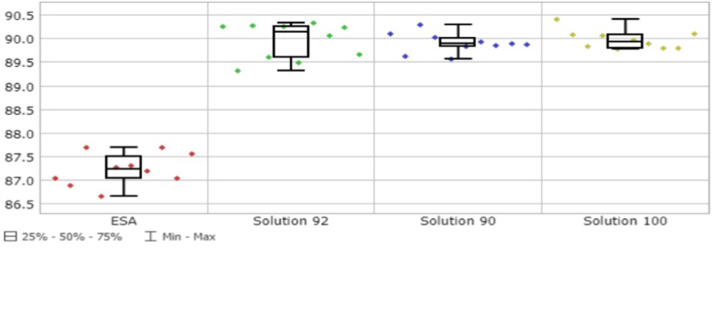
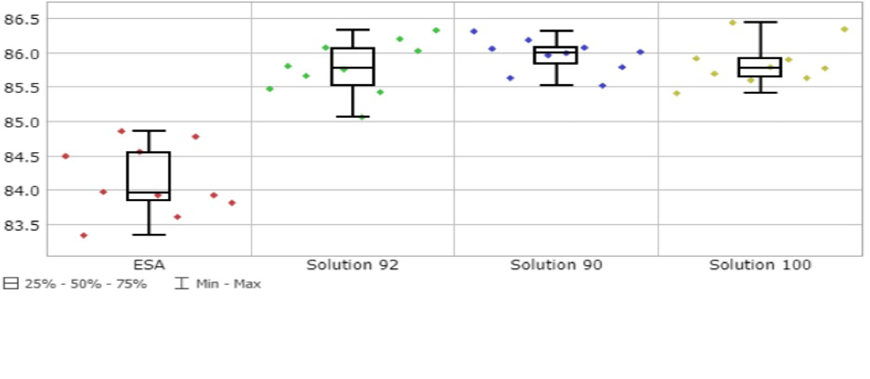
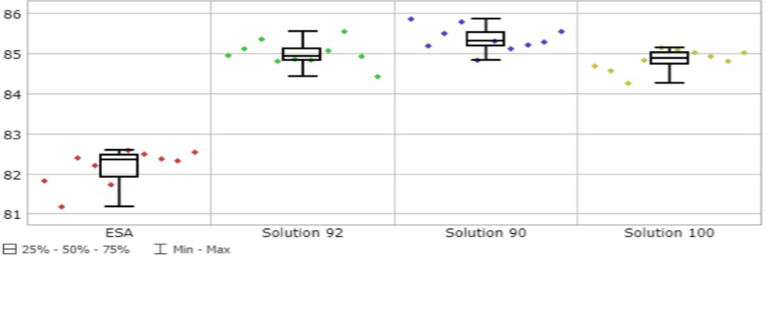
En este paso se obtuvieron los valores de las principales métricas de desempeño de la operación y relacionadas con el empleo de los recursos, tanto para los enebradores y viradores (UEi,j y UVi,j), como para las máquinas (Pk) (figura 7).

Respecto a ESA y de forma general, disminuyó la utilización de los trabajadores al emplear la misma cantidad de estos para producir un menor volumen de producción, salvo para (d,1) en la solución 92 que empleó un trabajador menos por lo que mejora el nivel de utilización.

Entre ellas las soluciones se comportaron de forma similar en valores medios y mostraron buena estabilidad al poseer desviaciones estándares que no superaron el 2% de variabilidad. Se destacaron con peores resultados las utilizaciones de los enebradores en (e,2) y (c,1) y de los viradores en (e,1) y en (d,1). Las secciones a y b fueron las que mejor emplearon a sus trabajadores con valores cercanos o superiores al 80% de utilización. La utilización de las máquinas mejoró respecto a ESA y entre ellas se comportaron de forma similar en valores medios y de desviación estándar, con valores por encima del 85% de utilización.

Figura 7. Ejemplos gráficos de la utilización de los recursos.

De las soluciones analizadas, sobresalió con relativos mejores resultados la solución 92 con un promedio de utilización de los enebradores y viradores de un 73.25% y un 73.45%, respectivamente. Además, con una utilización de las máquinas de un 86.84%, determinada por un 4.70% (5.78 horas) de breakdowns (variable B) y un 8.46% (10.41 horas) de espera por los enebradores para atender dichos breakdowns (variable WOM). Otras causas que afectaron el rendimiento; y por ende, la continuidad de los ítems, fueron las esperas por los viradores, ya fuere para el virado de las medias (variable WO), como para la transportación de las docenas a lo largo de toda la operación (variable WT), con un 5.42% (6.67 horas) y un 5.94% (7.31 horas), respectivamente.A lo anterior se añade que, para esta solución (92) se cumplió el plan de producción por encima del 95% y se alcanzó el 100% en la mayor parte de los casos.

Las disminuciones de la cantidad a producir de una semana a otra condicionaron las medidas a tomar en la asignación de los recursos. Para pasar de ESA (l-1) a la semana analizada (l) se sugirieron las medidas siguientes:Implementar la solución 92 por haber alcanzado menor CT y mayores CP y R. Además, logró mejores resultados en la utilización de los recursos hombres y máquinas.

1.Mantener la misma cantidad de trabajadores respecto a ESA, tanto de enebradores como de viradores, con la excepción de reubicar a un virador de (d,1) en (c,1).

2.Controlar la utilización de los trabajadores en aquellas subsecciones con peores resultados (enebradores en (e,2) y (c,1) y viradores en (e,1) y (d,1)), los cuales, de ser viable, pueden colaborar en el trabajo con las subsecciones a y b o con otras áreas de la fábrica.

Disminuir las cantidades de máquinas destinadas a las producciones de los diferentes tipos de ítems, es decir, conservarlas transitoriamente y de acuerdo a los resultados obtenidos en el cuadro 7.

Conclusiones

En este trabajo se integra la optimización, basada en la simulación de eventos discretos, con la asignación de recursos hombres y máquinas en los sistemas productivos, lo que demuestra el potencial de estas herramientas en la toma de decisiones. Al aplicar la lógica del modelo, de conjunto con sus funcionalidades programadas, se evidencia la determinación de un Plan Maestro de Producción factible y ajustado a los recursos existentes en la operación cuello de botella, el cual se ejecuta a un costo total mínimo, con altos niveles de cumplimiento del plan y con un buen aprovechamiento de los factores de producción disponibles. Además, dicha lógica permite identificar los mejores escenarios en los que deben ser asignados los trabajadores por cada una de las secciones y subsecciones de trabajo y las máquinas por cada tipo de ítem a producir. Dentro de estos escenarios colabora en detectar aquel o aquellos que garantizan el mejor desempeño del sistema y cuáles son las causas que mayormente influyen en la pérdida del rendimiento en la operación.

Al procesar la información, se selecciona la solución 92 como mejor alternativa en la que se deben organizar los recursos para la semana que se planifica. Esta solución propone un costo total mínimo de $ 34941.52, un cumplimiento del plan al 99.48% y un rendimiento de 1.52 docenas/minuto. Acompañados de utilizaciones del 73.25%, 73.45% y del 86.84% para los enebradores, viradores y máquinas, respectivamente. A partir de este estudio, el modelo puede ser enriquecido a partir de considerar la interacción de la operación cuello de botella con el resto de las operaciones, cuyas aleatoriedades pueden afectar la continuidad del trabajo y del flujo a lo largo del proceso productivo. Se añaden, posibles análisis acordes a la realidad actual de la industria textil de la zona y donde la subcontratación de ciertas operaciones se ha convertido en una alternativa para minimizar los costos totales de producción y para enfrentar las fluctuaciones en la demanda.

Referencias

[1] D. Singh, “You can use simulation to make the correct decisions,” Industrial Engineering, vol. 23, pp. 39-42, 1991.

[2] R. Roy and S. Grinsted, “The role of simulation in manufacturing and how to use it effectively,” in Proceedings of the 2nd International Conference on Simulation in Manufacturing: 24-26 June 1986, Chicago, USA, 1986, pp. 151-156.

[3] R. Schroeder, Administración de operaciones. Conceptos y casos contemporáneos. México DF: Editorial McGraw Hill, 2011.

[4] A. M. Law and D. W. Kelton, “Simulation modeling and analysis,” 2000.

[5] C. A. Goodsell and T. J. V. Kley, “Inventory management simulations at Cat Logistics,” presented at the Proceedings of the 32nd conference on Winter simulation, Orlando, Florida, 2000.

[6] J. García-Laguna, L. A. San-José, L. E. Cárdenas-Barrón, and J. Sicilia, “The integrality of the lot size in the basic EOQ and EPQ models: Applications to other production-inventory models,” Applied Mathematics and Computation, vol. 216, pp. 1660-1672, 2010/05/01/ 2010.

[7] L. E. Cardenas-Barron, N. R. Smith, J. L. Martinez-Flores, and M. Rodriguez Salvador, “Modelling lead time effects on joint inventory and price optimisation,” International Journal of Logistics Economics and Globalisation, vol. 2, pp. 270-291, 2010.

[8] L. A. San-José, J. Sicilia, and J. García-Laguna, “Optimal lot size for a production–inventory system with partial backlogging and mixture of dispatching policies,” International Journal of Production Economics, vol. 155, pp. 194-203, 2014/09/01/ 2014.

[9] J. O’Kane, “Simulating production performance: cross case analysis and policy implications,” Industrial Management & Data Systems, vol. 104, pp. 309-321, 2004.

[10] R. Mahanti and J. Antony, “Confluence of six sigma, simulation and software development,” Managerial Auditing Journal, vol. 20, pp. 739-762, 2005.

[11] I. H. Yavuz and A. Satir, “A kanban-based simulation study of a mixed model just-in-time manufacturing line,” International Journal of Production Research, vol. 33, pp. 1027-1048, 1995/04/01 1995.

[12] Y. Sugimori, K. Kusunoki, F. Cho, and S. Uchikawa, “Toyota production system and Kanban system Materialization of just-in-time and respect-for-human system,” International Journal of Production Research, vol. 15, pp. 553-564, 1977/01/01 1977.

[13] M. E. A. Boudella, E. Sahin, and Y. Dallery, “Kitting optimisation in Just-in-Time mixed-model assembly lines: assigning parts to pickers in a hybrid robot–operator kitting system,” International Journal of Production Research, pp. 1-20, 2018.

[14] L. Maleki, S. H. R. Pasandideh, S. T. A. Niaki, and L. E. Cárdenas-Barrón, “Determining the prices of remanufactured products, capacity of internal workstations and the contracting strategy within queuing framework,” Applied Soft Computing, vol. 54, pp. 313-321, 2017/05/01/ 2017.

[15] V. V. Kalashnikov, R. C. Herrera Maldonado, J.-F. Camacho-Vallejo, and N. I. Kalashnykova, “A heuristic algorithm solving bilevel toll optimization problems,” The International Journal of Logistics Management, vol. 27, pp. 31-51, 2016.

[16] J. SICILIA, J. FEBLES-ACOSTA, and M. GONZÁLEZ-DE LA ROSA, “DETERMINISTIC INVENTORY SYSTEMS WITH POWER DEMAND PATTERN,” Asia-Pacific Journal of Operational Research, vol. 29, p. 1250025, 2012.

[17] A. K. Bhunia, A. A. Shaikh, and L. E. Cárdenas-Barrón, “A partially integrated production-inventory model with interval valued inventory costs, variable demand and flexible reliability,” Applied Soft Computing, vol. 55, pp. 491-502, 2017/06/01/ 2017.

[18] E. Müller, J. Tolujew, and F. Kienzle, “Push-Kanban – a kanban-based production control concept for job shops,” Production Planning & Control, vol. 25, pp. 401-413, 2014/04/01 2014.

[19] P. L. Gonzalez-R, M. Calle, and J. L. Andrade-Pineda, “Job shop management of products under internal lifespan and external due date,” International Journal of Production Research, pp. 1-18, 2018.

[20] M.-S. Casas-Ramírez, J.-F. Camacho-Vallejo, and I.-A. Martínez-Salazar, “Approximating solutions to a bilevel capacitated facility location problem with customer’s patronization toward a list of preferences,” Applied Mathematics and Computation, vol. 319, pp. 369-386, 2018.

[21] J. F. Camacho Vallejo and R. Muñoz Sánchez, “A path based algorithm for solve the hazardous materials transportation bilevel problem,” in Applied Mechanics and Materials, 2013, pp. 1082-1088.

[22] M. R. Montoya, M. B. B. Loranca, R. G. Velázquez, J. L. M. Flores, H. B. Santos, A. S. Flores, et al., “A Solution Proposal for the Capacitated P-Median Problem with Tabu Search,” 2016.

[23] B. Beemsterboer, M. Land, R. Teunter, and J. Bokhorst, “Reprint of “Integrating make-to-order and make-to-stock in job shop control”,” International Journal of Production Economics, vol. 194, pp. 3-12, 2017/12/01/ 2017.

[24] M. Thürer, M. Stevenson, C. Silva, and T. Qu, “Drum-buffer-rope and workload control in High-variety flow and job shops with bottlenecks: An assessment by simulation,” International Journal of Production Economics, vol. 188, pp. 116-127, 2017/06/01/ 2017.

[25] Harrell, “Simulation Using ProModel: McGraw-Hill Education.,” 2011.

[26] J. A. Domínguez Machuca, J. Alvarez Gill, A. Domínguez Machuca, S. García González, and A. Ruíz Jímenes, Dirección de Operaciones. Aspectos Estratégicos en la producción y los servicios. España: McGraw_Gill, 1995.

[27] L. J. Krajewski, L. P. Ritzman, and M. K. Malhotra, “Administración de operaciones. Procesos y cadena de suministro,” ed: México: Pearson Educación, 2008.

[28] T. L. Saaty, The Analytic Hierarchy Process. New York: McGraw Hill 1981.

[29] E. Orozco Crespo and D. D. Hermoso Ayala, “Optimización del proceso de producción de medias corta logo en la fábrica Gardenia,” 2017-01-24 2017.

[30] E. Orozco Crespo and D. D. Hermoso Ayala, “Optimización del proceso de producción de medias corta logo en la fábrica Gardenia,” 2017-01-24 2017.

---