2.GENERACION-HTML

Evaluación de materiales semiconductores utilizando simulación numérica con elementos finitos para la producción termoeléctrica en condiciones de vacío

Evaluation of semiconductor materials usind finite-elments simulation for thermoelectric production in vaccum conditions

Adrián Quesada-Martínez1, Carlos Meza-Benavides2

Fecha de recepción: 26 de julio de 2018
Fecha de aprobación: 18 de setiembre de 2018

Quesada-Martínez, A; Meza-Benavides, C. Evaluación de materiales semiconductores utilizando simulación numérica con elementos finitos para la producción termoeléctrica en condiciones de vacío. Tecnología en Marcha. Vol. 32-2. Abril-Junio 2019. Pág 18-29.

DOI: https://doi.org/10.18845/tm.v32i2.4346

Palabras clave

Termoelectricidad; Efecto Peltier; Efecto Seebeck.

Resumen

Los materiales termoeléctricos (TE) son usados para la generación de energía eléctrica usando cuando existe un diferencial de temperatura en sus extremos. Esta característica de los materiales se perfila como una fuente de energía alternativa, sobre todo en aquellas condiciones en donde no existen otras fuentes, como por ejemplo en el espacio. Este articulo presenta la evaluación por medio de simulaciones numéricas con método de elementos finitos, de materiales semiconductores termoeléctricos para su uso en vacío en el espacio.

Keywords

Thermoelectricity; Peltier Effect; Seebeck Effect.

Abstract

Thermoelectric materials (TE) are used for the generation of electrical energy when there is a temperature differential at their ends. Thermoelectricity is emerging as an alternative energy source, especially in situations where there are no other sources, such as outer space. This article presents the evaluation by means of finite-element numerical simulations of different thermoelectric semiconductor materials used in outer space.

Introducción

En la generación termoeléctrica se utiliza principalmente Telururo de Bismuto (Bi2Te3), Telururo de Plomo (PbTe) y Silicio - Germanio (SiGe) ya que son los materiales que presentan rangos de temperatura de operación baja, media y alta respectivamente, además, presentan una buena combinación de las tres variables que se deben considerar en los materiales termoeléctricos, estas son: coeficiente Seebeck, conductividad eléctrica y conductividad térmica [1].

Los materiales son clasificados según el rango de temperatura en el que operan como sed muestra en el cuadro 1.

Cuadro 1. Clasificación de los semiconductores según su rango de temperatura.

Material	Clasificación de Temperatura	Rango de Temperatura
Telururo de Bismuto (Bi2Te3)	Baja	Hasta 450 K
Telururo de Plomo (PbTe)	Media	Hasta 850 K
Silicio-Germanio (SiGe)	Alta	Hasta 1300 K

En este documento se evalúa el comportamiento eléctrico del Bi2Te3 y PbTe ante cambios de temperatura que podrían experimentar estos materiales debido a la radiación solar en condiciones de vacío en el espacio.

El Efecto Seebeck para la Generación de Energía

El efecto termoeléctrico Seebeck describe el hecho de que un gradiente de temperatura impulsa la difusión de portadores cargados, que a su vez crea una tensión [2] [3]. El coeficiente de Seebeck de un material depende de la estructura del cristal, de la temperatura y del material. Los términos de energía termoeléctrica y termo potencia son nombres inapropiados ya que miden la tensión o el campo eléctrico (no la potencia eléctrica) inducido en respuesta a una diferencia de temperatura. Fundamentalmente, la termoeléctrica es una medida de la cantidad de entropía neta transportada por los portadores [4]. Los principales contribuyentes a la transferencia de entropía en la presencia de un gradiente de temperatura originados por difusión y / o los efectos de arrastre de fonones. Ambos efectos se observan en metales y semiconductores, sin embargo, uno domina típicamente sobre el otro. Por ejemplo, la difusión domina la termoeléctrica para la mayoría de los metales, mientras que el arrastre de fonones puede ser cien veces más grande que la difusión en los semiconductores.

Conversión de Potencia Termoeléctrica

El efecto Seebeck describe la generación de un gradiente de tensión termoeléctrico ΔV (la carga del electrón es -e, por lo tanto, e > 0 por un gradiente de temperatura ΔT, mientras que el efecto Peltier se refiere a la corriente de calor asociado con la corriente eléctrica [5].

Estos son los fenómenos termoeléctricos básicos que rigen la conversión del calor en energía eléctrica y viceversa en los conductores eléctricos. El efecto Peltier expresa la corriente de calor JQ en presencia de corriente eléctrica JC, definida como el flujo de carga, es decir, opuesta a la corriente de partículas

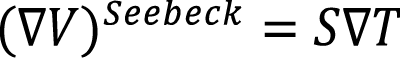(1)

(2)

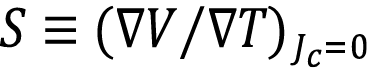Donde y 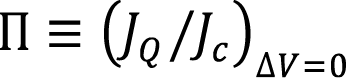son los coeficientes Seebeck y Peltier, respectivamente. Cuando el calor y corrientes eléctricas son uniformes en una sección transversal A, los vectores de corriente 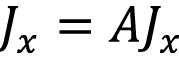se describen en términos de las densidades 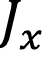actuales. Al combinar el efecto Seebeck con la ley de Ohm y efecto el Peltier con la ley de Fourier , donde σ y k son las conductividades eléctricas (en ) y térmicas (en ), las relaciones termoeléctricas tradicionales dicen que:

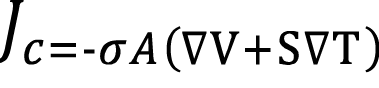(3)

(4)

Considere un conductor como el que se representa en la Figura 1. En z=0, la temperatura es , mientras que en z=l, la temperatura es , donde . De acuerdo con la ecuación (4), la corriente de calor JQ depende de la carga de corriente JC y el gradiente de temperatura dT/dz.

Cuando el anillo de corriente es cerrado por la resistencia de carga RCarga y

(5)

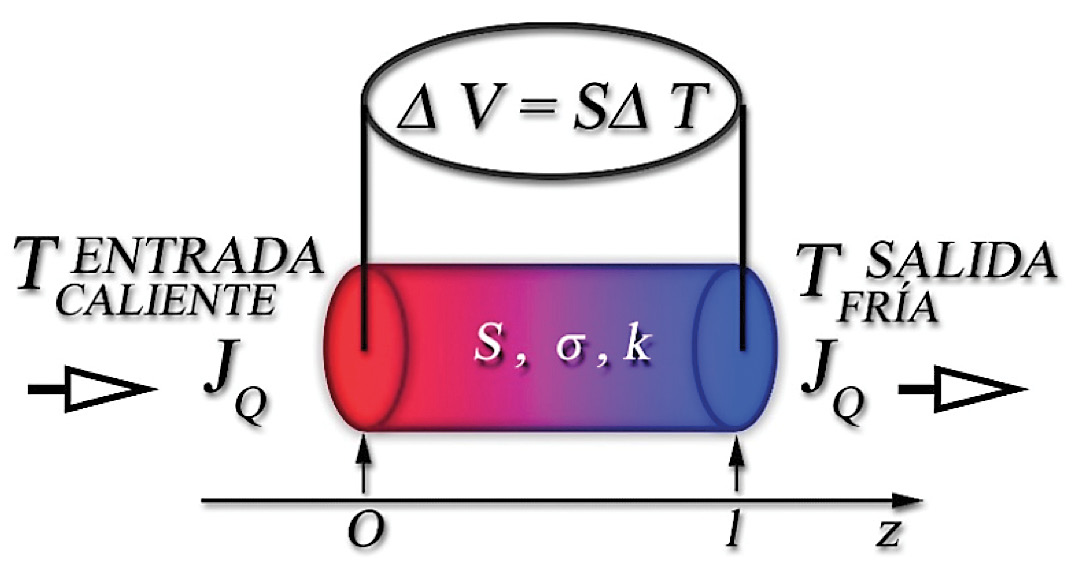
Figura 1. Elemento termoeléctrico que consiste en un hilo conductor cuyos extremos se mantienen a diferentes temperaturas TCaliente y TFría, generando una tensión termoeléctrica ΔV = SΔT = S(TCaliente - TFría).

Con , la tensión termoeléctrica es suprimida por el calentamiento Joule generado por la resistencia interna .

A continuación, se considera un dispositivo que consta de dos hilos conductores con coeficientes Seebeck Sp y Sn conectados en un lado, es decir, lo que se denomina como termopar. Las etiquetas se refieren a los semiconductores, en los que uno puede ser de tipo p y la otra de tipo n dopado tal que Sp > 0 y Sn < 0. El circuito está cerrado por una resistencia de carga externa RCarga (Figura 2). Las dos uniones se considera que tienen un buen contacto térmico para calentar los depósitos a temperaturas TCaliente y TFría. La diferencia en los coeficientes Seebeck induce EMF y crea una tensión ΔV sobre la carga a temperatura constante TFría. El trabajo realizado por el sistema es la disipación óhmica en la carga.

(6)

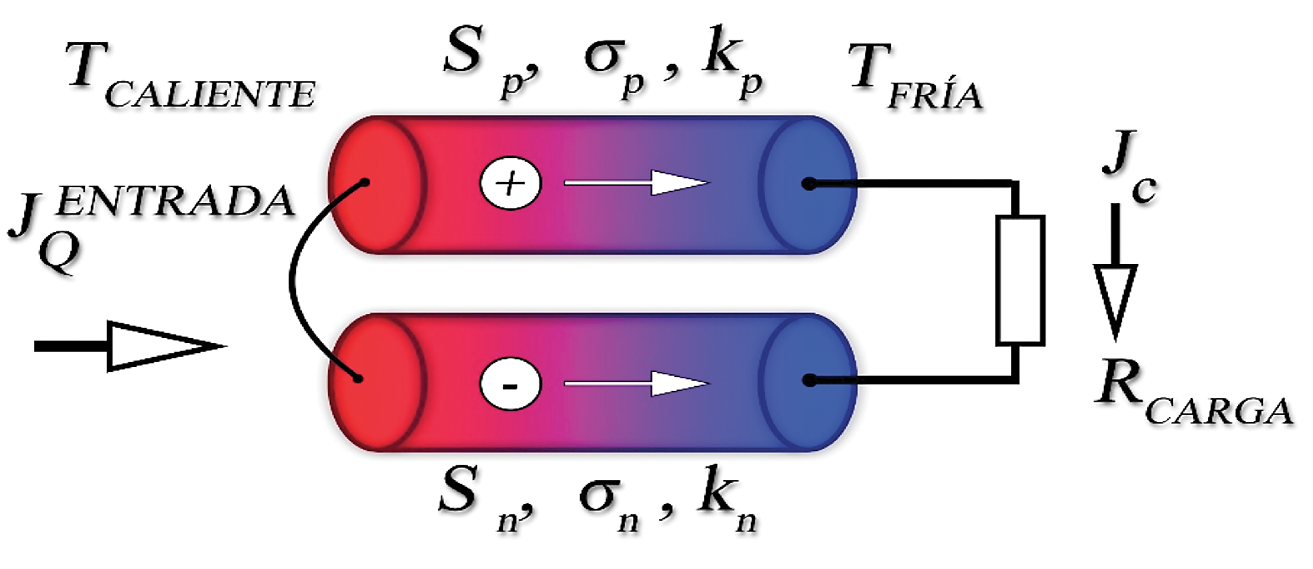
Figura 2. Termopar de dos conductores (por ejemplo, semiconductores, p y n dopados) que están conectados a una resistencia de carga RCarga bajo un sesgo de temperatura. La diferencia de coeficientes de Seebeck induce una polarización de tensión isotérmica sobre la resistencia de carga y conduce una corriente de carga a través del circuito.

Esta potencia depende de los signos de la diferencia de temperatura ΔT y no de la diferencia de los coeficientes Seebeck.

La tensión de salida se puede aumentar mediante la conexión de los termopares en serie para formar una termopila. La tensión de salida es lineal al número de elementos.

Eficiencia Termoeléctrica

Los dispositivos termoeléctricos ofrecen generación de energía y refrigeración, sin partes móviles y el funcionamiento es casi libre de mantenimiento [2] [3]. Una diferencia de temperatura a través de cualquier material no superconductor creara una tensión que se puede utilizar para proporcionar energía.

Una corriente a través de ese mismo material se puede utilizar para enfriar un extremo para fines de refrigeración. Se puede decir que la termoelectricidad es esencialmente un motor térmico de partículas, donde el fluido de trabajo se compone de electrones o agujeros. El reto excepcional en el estudio de termoelectricidad es encontrar materiales que pueden proporcionar la energía y la refrigeración a una alta eficiencia termodinámica. En la actualidad, la termoelectricidad se encuentra entre un veinte y treinta por ciento menos eficiente que la quema de combustibles fósiles en las centrales eléctricas y refrigeradores basados en compresores. Los principios termoeléctricos se encuentran bien definidos para materiales que se obtienen a granel y los más eficientes se basan en aleaciones de Bi2Te3 con eficiencias que rondan el 10% [5].

La eficiencia de un material termoeléctrico se determina según la figura de mérito:

Donde:

S es la potencia termoeléctrica, definida como la tensión termoeléctrica (V) producida por la diferencia de temperatura por grado.

σ es la conductividad eléctrica.

k es la conductividad térmica total, formadas por la contribución de fonones y electrones.

T es la temperatura.

La eficiencia se relaciona con ZT por la siguiente ecuación:

(7)

En la ecuación 7 se aprecia que la eficiencia tiende hacia el límite de Carnot cuando ZT tiende a infinito. Para competir con los refrigeradores modernos basados en compresores, el dispositivo termoeléctrico debe tener un ZT > 3. No hay límite teórico para ZT. Para maximizar ZT, S debe ser muy grande, de modo que una pequeña diferencia de temperatura pueda crear una gran tensión, σ debe ser muy grande con el fin de minimizar las pérdidas de calentamiento por efecto Joule, y k debe ser muy pequeño para reducir las fugas de calor y mantener una diferencia de temperatura [8]. S, σ, k no son mutuamente excluyentes. Por ejemplo, en un material a granel, la ley de Wiedemann-Franz limita la proporción σ/ ke, donde ke es la contribución electrónica a la conductividad térmica total.

Caso de estudio simulado y entorno de simulación

Los generadores termoeléctricos propuestos constan de patas verticales de Telururo de Bismuto como el material termoeléctrico. En sistemas donde las dimensiones horizontales y verticales son limitadas, estos convertidores de energía termoeléctrica miniaturizados se utilizan para convertir el calor residual en electricidad.

Hay fundamentalmente dos diseños introducidos en este trabajo, el primer generador consta en una pierna simple, mientras que, el segundo generador consta en una pierna doble conectada eléctricamente en paralelo mediante una placa de cobre, en donde se tiene Teleruro de Bismuto tipo p y n para cada una de las piernas como se muestra en la figura 3.

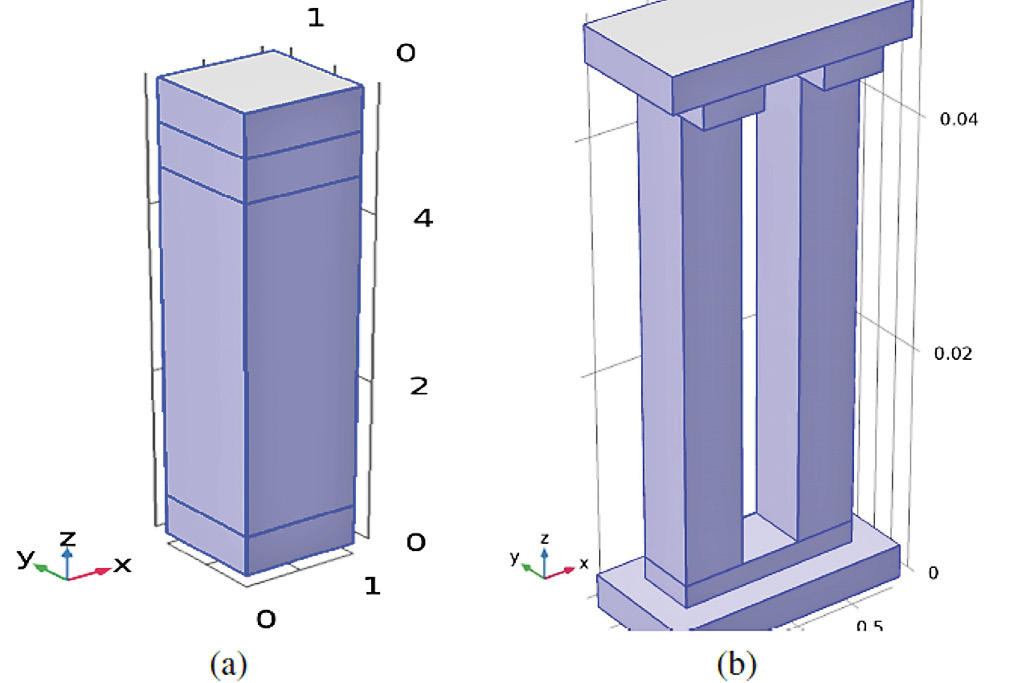
Figura 3. (a) Generador de pierna simple. (b) Generador de pierna doble.

En ambos TEG’s los extremos superiores son de aluminio, cara en la que se inicia la transferencia de calor por radiación. El segundo elemento consta de una placa de cobre, donde se conectarán los electrodos para la conducción de la tensión, y por último, el semiconductor encargado de la producción de tensión a partir de la diferencia de temperatura.

La cara de aluminio expuesta a la radiación solar es donde inicia la transferencia de calor de los generadores, y se asume una temperatura de entrada o de exposición máxima de 100°C.

Además, se asumió una temperatura en el interior del TEG de 0 °C, ya que de la misma manera que, se asumió que la radiación solar incide únicamente en una cara del material de aluminio, ya que los demás materiales no tendrán exposición directa a la radiación.

Con base en esto, se tomaron las demás caras del generador aisladas térmicamente, ya que estas no tendrán exposición a la radiación solar, la cual sería el mayor aporque de temperatura al generador.

La simulación de los dos tipos de generadores se realizó utilizando el software COMSOL Multiphysics ®, para esto se siguieron los siguientes pasos.

Se selecciono un estudio en 3D, se agregaron la física y multi física aplicadas en la simulación: Mecánica de Solidos y Efecto Termoeléctrico (esta trae las físicas de Transferencia de Calor y Corrientes Eléctricas), se seleccionó un estudio transitorio.

Las geometrías se definieron como se observa en la figura 4 y se seleccionaron los materiales de cada TEG. Cobre-Telururo de Bismuto-Cobre-Aluminio, para el primer generador y Cobre-Telururo de Bismuto tipo p-Telururo de Bismuto tipo n-Cobre-Aluminio para el segundo generador.

En la física de Transferencia de calor se definió una condición de borde de temperatura inicial de 100°C en la cara superior del aluminio.

En la física de Mecánica de sólido, en la sección “Linear Elastic Material”, se selecciono “Thermal Expansion” y en la sección de “Thermal Expansion”, en “Tref” se definió una temperatura de 100°C. Se definió una condición de borde de “Fixed Constraint”, el cual evita de forma puntual que la pieza se deforme, este se colocó en las 4 esquinas bajo el cubo de cobre que se encuentra más alejado a la temperatura de 100°C en el aluminio. Además, tiene como objetivo que la pieza se encuentre estáticamente determinada para que la simulación se lleve a cabo.

Se acoplo la física de Mecánica de Solidos a la de Transferencia de Calor, ya que la de Corrientes Eléctricas ya se encontraban acopladas.

Se definió una malla tetraédrica con tamaño extrafina y en “Study”, se estableció un rango de tiempo de 0 a 5 segundos, con un paso de 0.1 s.

Una vez que termino de correr la simulación, se presentan los resultados de transferencia térmica, voltaje y esfuerzo al que está sometido el TEG y se obtuvo el resultado de desplazamiento y densidad de corriente normal en el menú de opciones de sus físicas respectivas.

Discusión y resultados de simulación

Se realizaron diferentes mediciones con los materiales que presentan temperaturas de operación bajas (Telururo de Bismuto y Telururo de Plomo), esto para realizar una comparación entre el comportamiento de ambos materiales utilizados para TGEs. En cada una de estas simulaciones se obtuvieron los valores de la tensión en la entrada del TEG y la tensión en la cara de salida del TEG en función de la temperatura de entrada.

En el caso del TEG cuya pierna se realizó con Telururo de Bismuto se aplicó un rango de temperatura en la cara de entrada desde 100 K hasta 450 K para observar el comportamiento de la tensión a lo largo del TEG, este rango de temperatura se definió según la temperatura máxima de operación del material seleccionado de acuerdo con el cuadro 1. Los resultados de todas las mediciones obtenidas para el Bi2Te3 se muestran en el cuadro 2.

Cuadro 2. Resultados de la simulación termoeléctrica para la pierna simple de Bi2Te3.

T (K)	Tin (°C)	Vin (V)	Vout (V)	Jin (A/mm2)	Jout (A/mm2)	Tout (°C)
100	-160	10	20	4,9400 × 106	1,050000 × 105	-20
150	-123	7,25	-13	1,2435 × 106	9,100000 × 104	-20
200	-74	4	-7	1,5200 × 106	1,860000 × 105	-20
250	-24	0,24	-0,3	1,4680 × 106	1,460000 × 105	-20
300	27	-3,5	6	5,8500 × 104	1,880000 × 105	-20
350	77	-7	13	1,3460 × 104	4,100000 × 104	-20
373,15	100	-9	16	4,3140 × 106	1,230000 × 105	-20
400	127	-11	19	8,8870 × 107	2,720000 × 106	-20
450	176	-14	25	3,1300 × 106	1,150000 × 105	-20

El mismo procedimiento se realizó para el caso del TEG cuya pierna se realizó con Telururo de Plomo, en donde se aplicó un rango de temperatura en la cara de entrada desde 100 K hasta 850 K. Este rango de temperatura se definió nuevamente tomando la temperatura máxima de operación del material de acuerdo con el cuadro 1. Los resultados de todas las mediciones obtenidas para el PbTe se muestran en el cuadro 3.

En la primera columna del cuadro se tiene la temperatura configurada a la entrada del elemento de aluminio que es la que iniciaría la transferencia de calor; en la segunda columna se tiene la temperatura en la entrada del TEG; las tensiones indicadas en las siguientes columnas corresponden a la tensión en el punto de entrada (Tin) y la tensión en el punto de salida (Tout) del TEG; por último, se tiene la densidad de corriente (J) en la entrada y en la salida del TEG y la temperatura en el punto de salida del TEG (Tout).

Cuadro 3. Resultados de la simulacio orriente (J) en la entrada y en la salidaPbTe.

T (K)	Tin (°C)	Vin (V)	Vout (V)	Jin (A/mm2)	Jout (A/mm2)	Tout (°C)
100	-173	4,2	-8,5	1,8426 × 108	2,5300 × 106	-20
150	-123	3	-6	6,7400 × 106	1,1700 × 105	-20
200	-73	1,43	-3	4,8620 × 106	1,3000 × 105	-20
250	-23	0	-0,2	6,3700 × 105	3,8000× 104	-20
300	26	-1,5	3	1,1280 × 106	2,9800 × 105	-20
350	77	-3,2	6,5	4,8900 × 105	1,5300 × 104	-20
375,15	100	-4	8	1,8520 × 106	5,6000 × 104	-20
400	126	-6,3	9,2	4,4400 × 105	7,8000 × 104	-20
450	177	-7,5	15	1,5350 × 107	5,1500 × 105	-20
500	227	-10	20	1,0066 × 109	1,5000 × 107	-20
550	277	-13	26	1,8602 × 108	1,6200 × 106	-20
600	326	-16	33	2,2610 × 108	6,0000 × 106	-20
650	377	-20	40	4,0600 × 108	4,4000 × 106	-20
700	426	-24	48	3,0490 × 109	1,8200 × 107	-20
750	477	-28	56	2,2490 × 108	4,3000 × 106	-20
800	526	-32	64	6,6840 × 108	9,6000 × 106	-20
850	578	-36	73	5,9800 × 108	6,8000 × 106	-20

Cada uno de los valores se tabularon para ser graficados y poder observar el comportamiento de las tensiones generadas conforme la temperatura de entrada iba cambiando.

Una vez que se establecía un valor de temperatura se definía el valor aproximado del coeficiente de Seebeck de acuerdo con las figuras de mérito de cada material.

En la figura 4 se puede observar que la tensión disminuye con una tendencia lineal en la entrada del TEG conforme la temperatura va en aumento, mientras que, la tensión en la cara de salida en función de la temperatura va en aumento conforme aumenta la temperatura.

Además, se aprecia que la tensión toma valores positivos y negativos por arriba o por debajo de la temperatura de equilibrio, este comportamiento es el esperado de acuerdo con lo establecido en la ecuación 3.

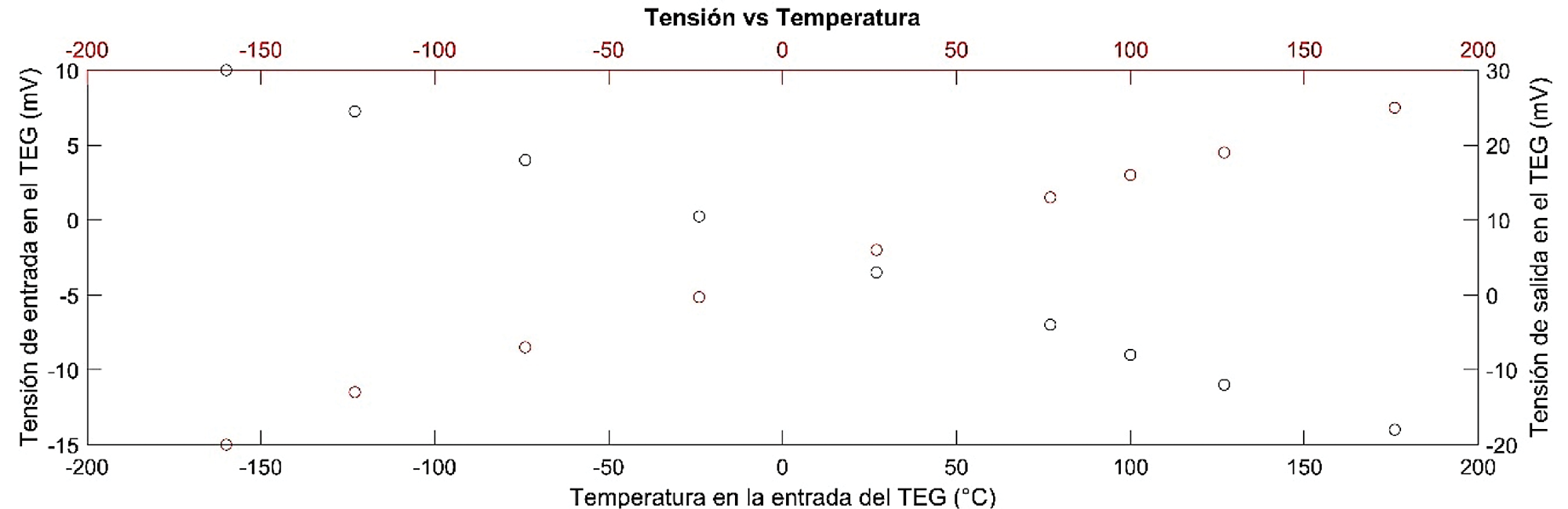
$D:\Usuarios\adquesada\AppData\Local\Microsoft\Windows\INetCache\Content.Word\BiTeTinTout1puntos3.jpg$

Figura 4. Tensión de entrada y de salida en función de la temperatura del TEG de Bi2Te3.

En la figura 5 se puede observar un comportamiento similar al del Bi2Te3 para el PbTe, con valores absolutos mucho más grandes que los del material anterior y con una tendencia cuadrática. Este material alcanza el cero de la ecuación en un valor de temperatura aproximado de 500 °C, mientas que el Bi2Te3 lo hace a un valor cercano a 28 °C.

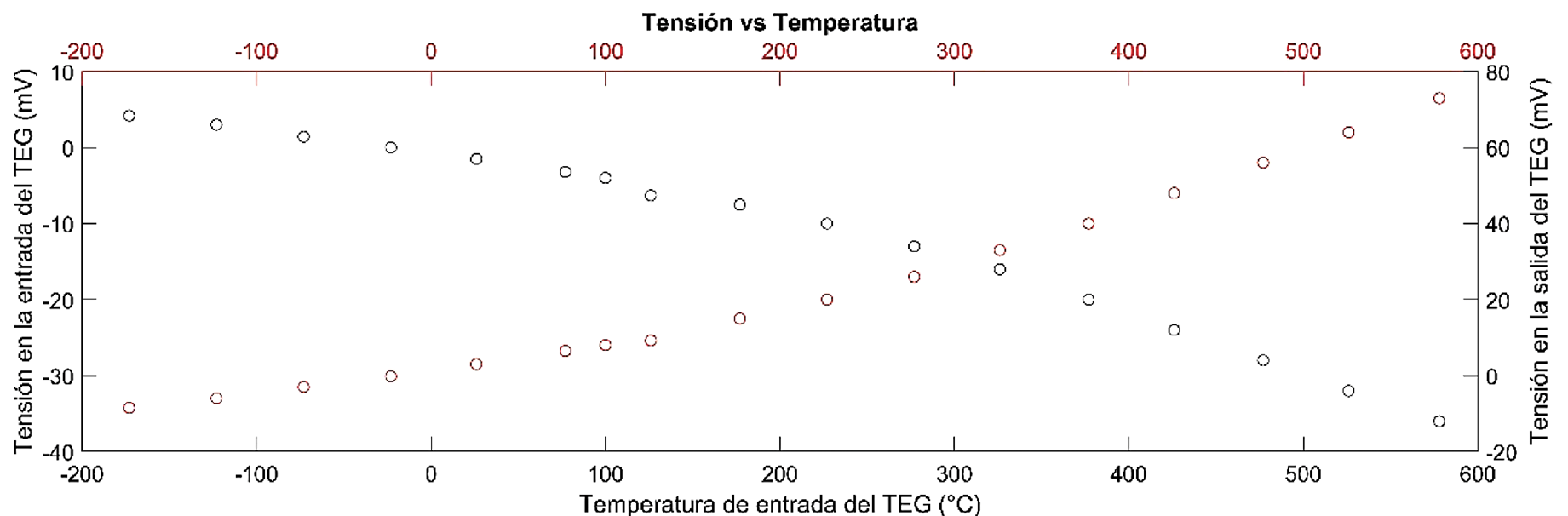
$D:\Usuarios\adquesada\AppData\Local\Microsoft\Windows\INetCache\Content.Word\PbTeTinTout2.jpg$

Figura 5. Tensión de entrada y de salida en función de la temperatura del TEG de PbTe.

Una vez que estos materiales pasan el cero de la ecuación, los valores de la tensión toman valores positivos y se puede observar que el Bi2Te3 toma estos valores a temperaturas más bajas de la temperatura máxima que puede alcanzar el TEG en condiciones de vacío en el espacio, e inclusive a temperaturas mucho más bajas que el PbTe.

El PbTe muestra una generación de tensión, en valor absoluto, mucho mayor que el Bi2Te3; que muestra una generación de tensión inclusive con cambio de signo en el intervalo de operación de temperatura.

Con los resultados obtenidos para la densidad de carga, se realizaron los gráficos con los valores de entrada y de salida para cada uno de los materiales, esto para poder observar el comportamiento de los valores conforme aumentaba la temperatura.

Los dos materiales presentan un comportamiento similar en las densidades de carga como se puede apreciar en la figura 6 y la figura 7 respectivamente, sin embargo, el PbTe muestra el punto más alto de los valores alrededor de los 426 ento similar en las BiTe presenta este punto alrededor de los 127 °C.

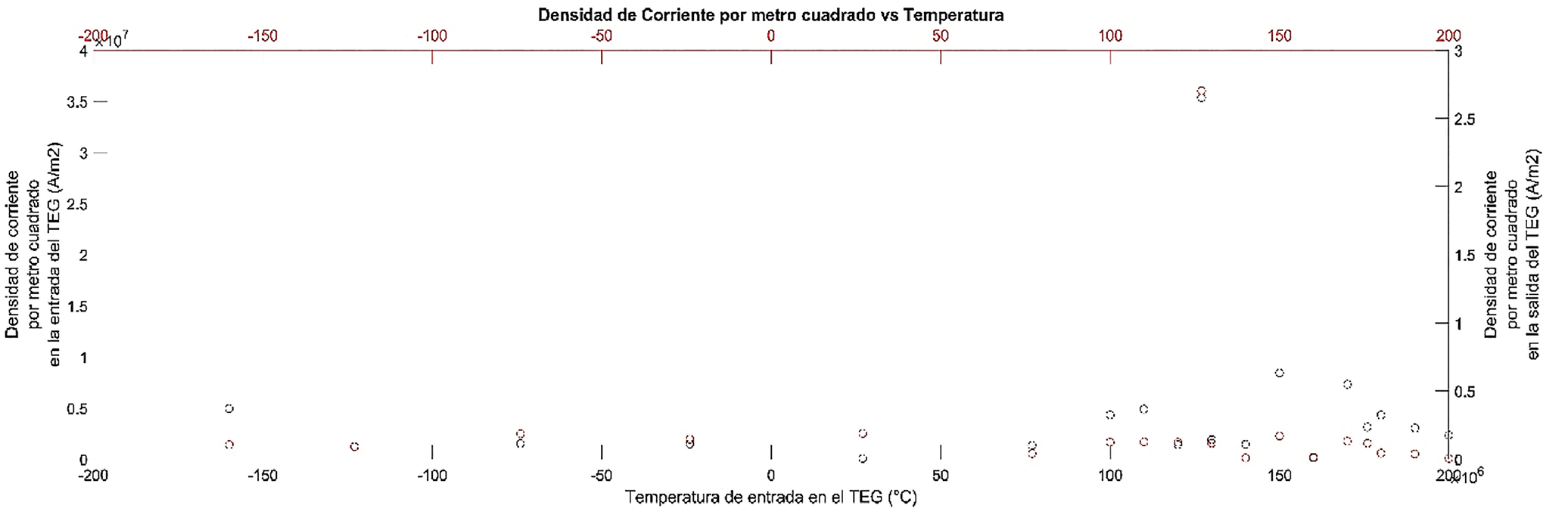
$D:\Usuarios\adquesada\AppData\Local\Microsoft\Windows\INetCache\Content.Word\BiTeJinJout3.jpg$

Figura 6. Densidad de carga por metro cuadrado de entrada y de salida en función de la temperatura del TEG de BiTe.

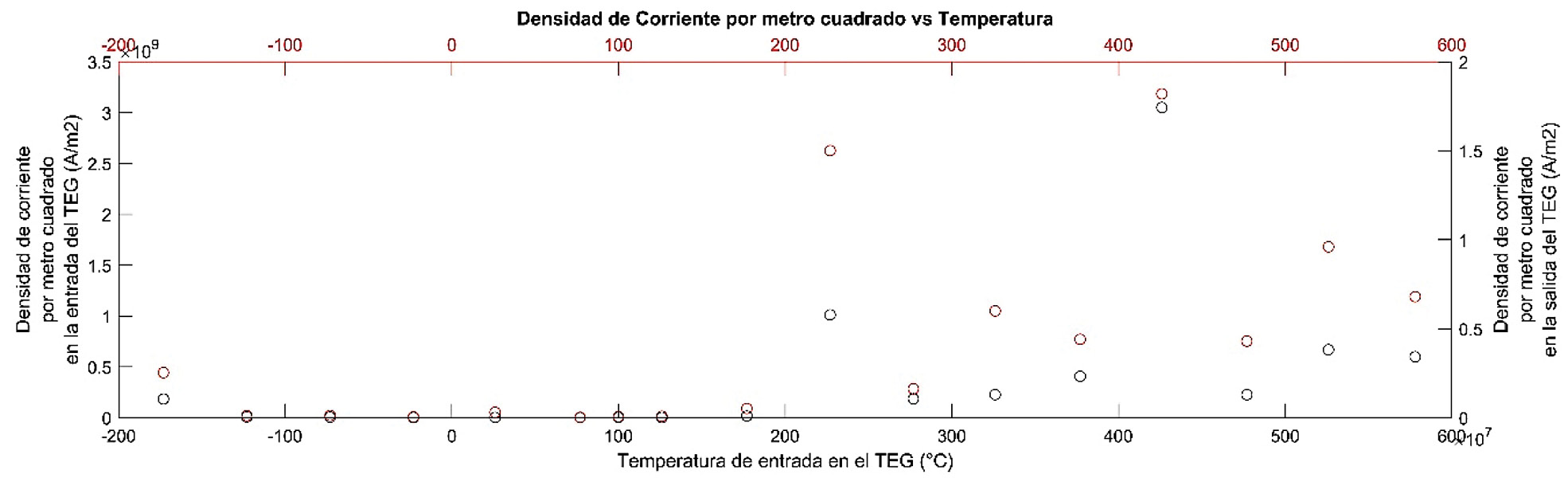
$D:\Usuarios\adquesada\AppData\Local\Microsoft\Windows\INetCache\Content.Word\PbTeJinJout2.jpg$

Figura 7. Densidad de carga por metro cuadrado de entrada y de salida en función de la temperatura del TEG de PbTe.

A la simulación realizada se le acoplo una resistencia de carga de 200 ohm. Este valor es la carga que representan las baterías completamente vacías del sistema de respaldo de un CubeSat para simular la carga de estas.

La ecuación 5 permite calcular el valor de la tensión de carga una vez que el circuito es cerrado por una resistencia de carga. Con el valor de la resistencia de carga de las baterías y esta ecuación, se realizó el cálculo de las tensiones de carga según el valor de la tensión en circuito abierto en función de la temperatura y se graficaron para ambos materiales para obtener un gráfico de tensión de carga en función de la temperatura como se muestra en la figura 8.

En esta grafica se observa que el Bi2Te3 toma valores de tensión de carga crecientes, con tendencia lineal, entre los rangos de operación del TEG, lo que hace que estos valores sean bajos alrededor de los -20 stos valores seanura teriPbTe los valores de tensión de carga crecen con una tendencia exponencial alrededor de los -10 °C, lo que hace que estos valores crezcan de una forma más rápida que el anterior.

Con la diferencia de tensión (ΔV) entre la entrada y la salida del TEG multiplicada por la densidad de carga (Jc) se obtuvo el valor de la potencia de salida del generador por unidad de área. Con estos resultados se obtiene un gráfico para cada material donde se puede estimar el punto de operación de estos generadores en función de la temperatura de entrada.

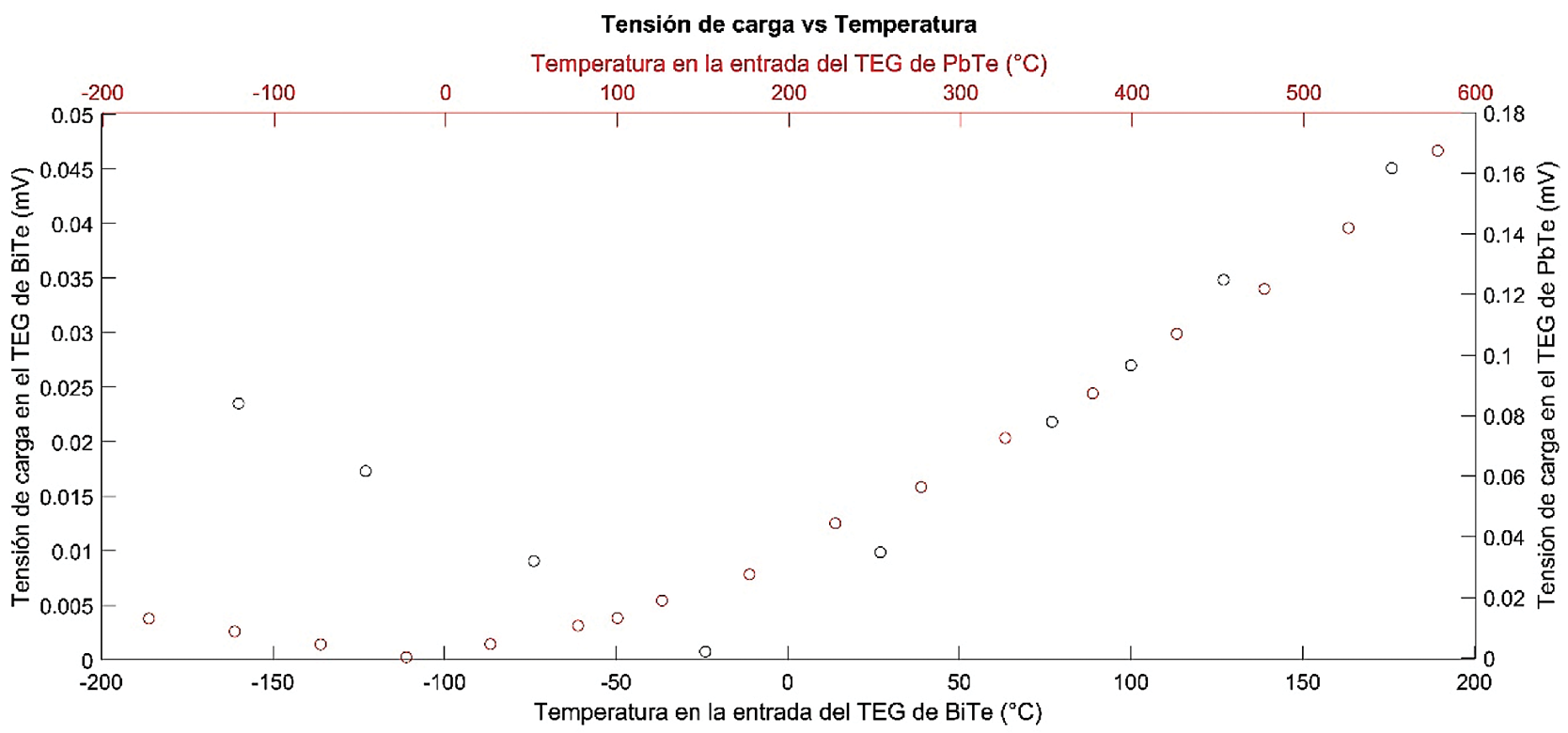
$D:\Usuarios\adquesada\AppData\Local\Microsoft\Windows\INetCache\Content.Word\Tensioncarga.jpg$

Figura 8: Tensión de carga en función de la temperatura del TEG.

Los gráficos para cada uno de los materiales se pueden observar en las figuras 9 y 10, para el Bi2Te3 y el PbTe respectivamente. En estas figuras se puede apreciar que el generador realizado con el Bi2Te3 presenta un valor de potencia máximo alrededor de los 127 °C, cuyo valor es aproximadamente 8.16 A/cm2, mientras que el PbTe presenta este punto máximo alrededor de los 426 °C, con un valor aproximado de 131.04 A/cm2.

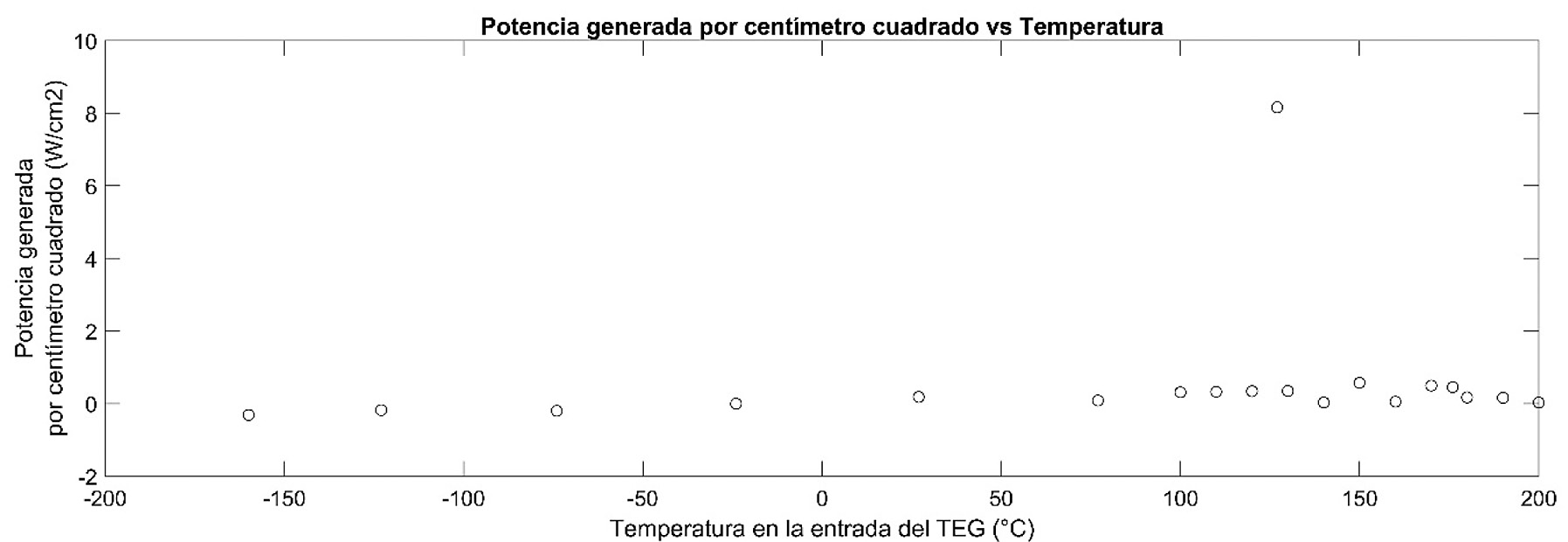
$D:\Usuarios\adquesada\AppData\Local\Microsoft\Windows\INetCache\Content.Word\BiTePout.jpg$

Figura 9: Potencia generada por centímetro cuadrado en función de la temperatura del TEG para el Bi2Te3.

El valor máximo de potencia por centímetro cuadrado que presentan estos materiales en los puntos indicados es un valor único en la distribución de los datos, este punto concuerda con el valor máximo del coeficiente de Seebeck.

Conclusiones

Las condiciones más optimas de potencia generada y tensión las presenta el Bi2Te3, por esta razón se recomienda este material para la fabricación de los TEGs para uso en vacío en el espacio, a pesar de que el PbTe presente valores más altos de tensión y potencia generada, queda fuera de esta aplicación porque para alcanzar valores utilizables se requieren temperaturas más altas.

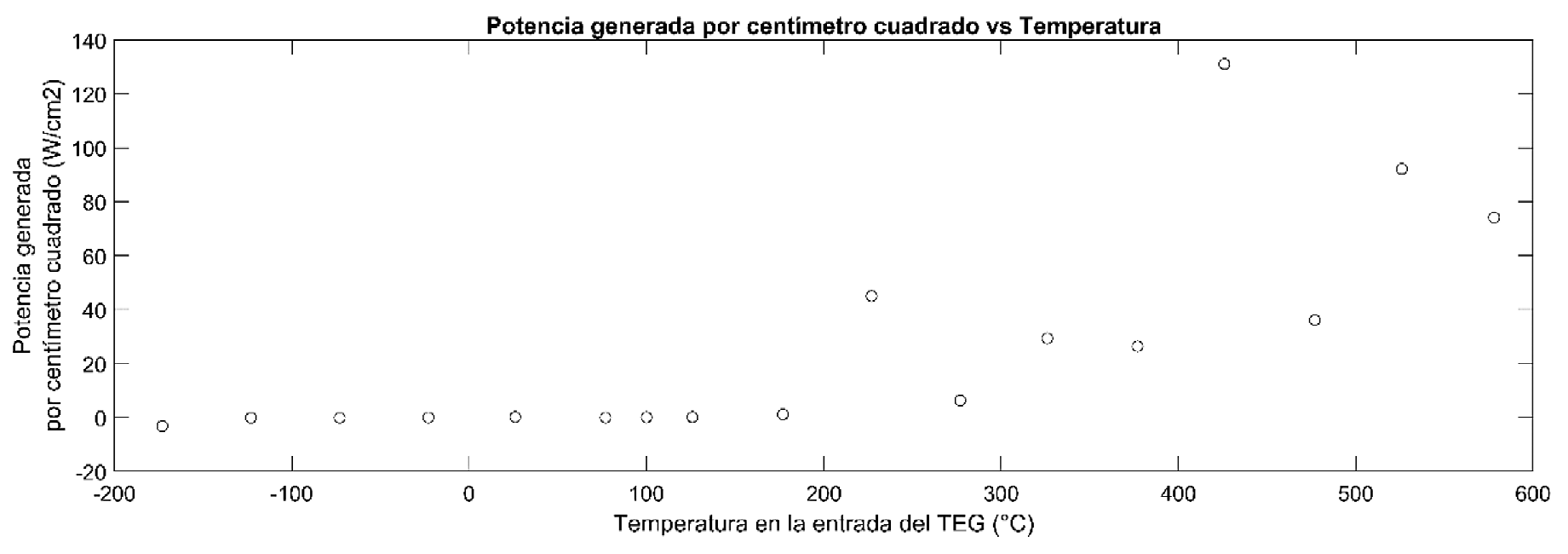
$D:\Usuarios\adquesada\AppData\Local\Microsoft\Windows\INetCache\Content.Word\PbTePout.jpg$

Figura 10: Potencia generada por centímetro cuadrado en función de la temperatura del TEG para el PbTe.

A pesar de que ambos materiales presenten un pico de potencia muy alto, no es recomendable trabajar con este valor, ya que, en los alrededores de este, decrece y crece la potencia de una forma muy rápida, lo que podría hacer que un pequeño cambio de temperatura genere un gran cambio en la potencia generada.

El material que se escogió para los módulos termoeléctricos son compuestos cuya base es Bi2Te3. Estos compuestos son comerciales, lo que quiere decir que a pesar de haber sido escogidos como los mejores materiales termoeléctricos para el rango de temperatura del TEG con la cual se trabajó durante el proyecto, no lo son. La investigación sobre materiales con un ZT más alto a bajas temperaturas, el uso de nuevos materiales en este campo de estudio y la aparición o creación de mejores compuestos, teorías de creación de materiales y modificación de los ya existentes permite pensar que con el paso del tiempo saldrán a la venta más y mejores opciones de materiales termoeléctricos.

Agradecimientos

Los autores expresan su agradecimiento al “Programa de Maestría en Ing. Electrónica” por facilitar el desarrollo de este proyecto.

Referencias

[1] M. D. Solís, “Diseño de Paneles Generadores de Electricidad por Efecto Seebeck,” Antioquia, 2013.

[2] D. MacDonald, Thermoelectricity: An Introduction to the Principles, Dover Books on Physics. Dover Publications, 2013.

[3] G. S. B. a. S. J. Mahan, Thermoelectric Materials: New Approaches to an Old Problem, Physics Today, 50(3):42., 1997.

[4] H. Callen, Thermodynamics, New York, NY: Wiley, 1985.

[5] D. Rowe, CRC Handbook of Thermoelectrics, CRC Press, 1995.

[6] S. de Groot, Thermodynamics of Irreversible Processes, North-Holland, 1966.

[7] L. Onsager, “Reciprocal relations in irreversible processes,” Phys. Rev, vol. 37, pp. 405-426, 1931.

[8] G. D. M. S. D. G. F. J.-P. a. C. T. Chen, G. Chen, M. Dresselhaus, G. Dresselhaus, J.-P. Fleurial and T. Caillat, “Recent developments in thermoelectric materials,” International Materials Reviews, vol. 48, no. 1, pp. 45-66, 2003.

[9] M. a. M. N. F. Cutler, “Observation of anderson localization in an electron gas,” vol. 181, p. 1336–1340, 1969.

[10] X. H. Yang, “First principles study of seebeck coefficients of doped semiconductors,” Journal of Applied Physics, vol. 111, no. 3, 2012.

1 Profesor, Escuela de Ciencia e Ingeniería de los Materiales, Instituto Tecnológico de Costa Rica. Correo electrónico: adquesada@tec.ac.cr

2 Profesor adjunto, Escuela de Ingeniería Electrónica, Instituto Tecnológico de Costa Rica. Correo electrónico: cmeza@tec.ac.cr