Potencia Reactiva: Despacho Óptimo con una programación lineal-PARTE A

Reactive Power: Optimal Dispatch with linear programming-PART A

Gustavo Adolfo Gómez-Ramírez1

Fecha de recepción: 25 de mayo de 2017
Fecha de aprobación: 26 de julio de 2018

Gómez-Ramírez, G. Potencia Reactiva: Despacho Óptimo con una programación lineal-PARTE A. Tecnología en Marcha. Vol. 32-1. Enero-Marzo 2019. Pág 25-38.

DOI: https://doi.org/10.18845/tm.v32i1.4116

Palabras clave

Potencia reactiva; despacho económico; programación lineal.

Resumen

La toma de decisiones se basa en aspectos técnicos, legales, pero sobretodo económico, no obstante, se requiere de gran experiencia del negocio para de esta manera ser acertado y tratar de no impactar negativamente. En el siguiente trabajo de investigación parte A, plantea un despacho óptimo de potencia reactiva a partir de la utilización de una optimización por programación lineal; dicha potencia es de gran importancia en los Sistemas Eléctricos de Potencia para el control y regulación de los perfiles de tensión. De igual forma contribuye en el flujo de potencia real de las líneas de transmisión. Por otro lado, es importante señalar, que los sistemas eléctricos a nivel mundial, no cuantifican su uso ni establecen valores para su cobro, por lo que el aporte de esta investigación va más allá de utilizar una herramienta de fácil uso, sino de proponer estructuras tarifarias donde se incluyan costos por el uso de la potencia reactiva y de esta manera disminuir los precios de la electricidad. Por último, en el presente trabajo se desarrolla en un sistema de potencia tipo IEEE-14.

Keywords

Reactive power; economic dispatch; linear programming.

Abstract

The decision-making is based on technical, legal, but especially economic facts; it requires business experience in order to be successful and try to have the smallest impact as possible. In the following research part-A, it proposes an optimal dispatch of reactive power and to use linear programming. This power is relevant in the Electrical Power Systems for the voltage´s control and regulation, and it contributes to the real power flow too. On the other hand, it is important to point out that the world’s power systems do not quantify their use nor establish prices; this research uses an easy tool, recommends a new rate´s structures and in the future can be a way to reduce it. Finally, this work develops an IEEE-14 power system.

Introducción

Los primeros sistemas eléctricos de potencia fueron desarrollados alrededor del año 1900, muchos de ellos, por su naturaleza tienen carácter público, semiprivado y privado, ya que por razones económicas muchas veces los gobiernos no asumieron la responsabilidad de la electrificación de los países. Hoy día la cadena de valor está integrada por la Generación, Transmisión, Distribución y Comercialización de electricidad. Gran parte de los servicios privados son la generación y la distribución, no obstante, la transmisión por lo general es un monopolio natural del estado debido a la alta inversión que esta implica.

La importancia de establecer mecanismos para las tarifas por el servicio, uso de la electricidad y ante todo definir de las estructuras de los costos para cada una de las componentes del sistema eléctrico, corresponden esencialmente a las áreas financieras y de comercialización de las empresas. En algunos casos se han establecido mercados eléctricos para ofrecer una gama de posibilidades de diferentes servicios en cuanto a la oferta y demanda definidos por el mercado.

Estado actual de la cuestión del despacho de potencia reactiva

Hsu y Chen en 2000 [1], cuestionan si dentro del esquema de la prestación del servicio eléctrico queda claro la responsabilidad de la compensación de potencia reactiva, quienes deben asumir los costos, si los consumidores finales deben pagar los costos de la potencia reactiva, o por el contrario las empresas generadoras de electricidad deben asumir este rol?. Por último, se hace un análisis de casos de sistemas eléctricos sin compensación de la potencia reactiva, con sistemas compensados parcial y completamente en los nodos de interconexión valorando la mejor opción para el sistema propuesto.

Miller en 2001 [2], plantea los métodos para la asignación de los peajes en los sistemas de transmisión eléctrica de acuerdo con su uso. En esta referencia se repasan todos los sistemas de las tarifas y se propone un método de cálculo para tarifas eléctricas. Doña y Paredes [3] proponen una estructura en los precios en mercados competitivos usando para el cálculo las pérdidas de transmisión. Se basa en la teoría de los costos marginales y las otras técnicas de optimización.

Tovar et ál. en 2002 [4] proponen una metodología basada en la sensibilidad para asignar los costos de los servicios del control de tensión y la potencia reactiva en los mercados eléctricos desregulados, en ella se distribuyen los costos de la potencia reactiva y estos servicios se distribuyen con base a sensibilidades relativas relacionadas con la tensión de los nodos de la carga y la generación. Tequitlapa [5] plantea una asignación de cargos por servicios del control de tensión y las reservas reactivas para el mercado de energía. Se plantean las posibles metodologías para los análisis de costos, realiza un análisis económico de la situación y por último una metodología de análisis para la asignación de los cargos. Zhong y Bhattacharya [6] plantean una administración de la potencia reactiva en los mercados eléctricos desregulados, en ella se hace una revisión de los distintos hitos históricos acontecidos en la última década del estudio en cuestión. Se mencionan los problemas tanto de la regulación de la tensión como de la frecuencia, se exponen algunos mecanismos para las propuestas de compensación financiera dentro de los parámetros regulatorios de cada país. Laguna [7] asigna los cargos por porteo de potencia real y la reactiva en los sistemas de transmisión, en la cual se analiza el método del rastreo de la potencia reactiva y establece una asignación de los costos a través de varios modelos aplicándolo a varios mercados internacionales.

Cortez en 2003 [8] plantea un análisis para establecer los precios para la potencia reactiva en los mercados descentralizados y competitivos. En ella se estudia la problemática del cobro de las tarifas en Chile y hace un recorrido por diversos mercados mundiales para estudiar la problemática. Macías y Pérez [9] analizan la regulación de las tarifas y la liberación del sector eléctrico español. Propone algunas alternativas de regulación de las tarifas para el transporte de la energía. Dan una perspectiva del impacto de la regulación en el mercado español.

Barragán y Robles en 2006 [10] propone el costo por el soporte de la tensión de los generadores en los sistemas eléctricos con el despacho centralizado y en él se plantean soluciones para establecer costos variables para el soporte de la tensión, de esta manera se obtiene una curva de capacidad y el costo de oportunidad por colocar la potencia. Se hace la evaluación en un sistema eléctrico de 30 nodos.

Carbajo en 2007 [11] analiza el mercado español y explora los servicios de ajuste dentro del sistema eléctrico, e incluye los servicios complementarios, la regulación primaria, secundaria y terciaria, así como las implicaciones en la tensión de la red eléctrica. Oh y Thomas [12] establecen los precios de la potencia reactiva en los mercados eléctricos desregulados proponiendo nuevas oportunidades de explotación de los mercados eléctricos tanto para la venta de la potencia activa como la reactiva. Lo analiza a través de la teoría de juegos.

Valenzuela en 2008 [13] estudia los efectos económicos que conllevan la prestación de los servicios auxiliares y se analizan los diversos escenarios en diferentes mercados mundiales, así como las propuestas de bajo costo dentro de los mercados eléctricos. Adicionalmente se desarrolla el problema del control de la tensión y establece una relación para con los mercados eléctricos.

Rabiee et ál. en 2009 [14] analizan el valor de la potencia reactiva en un sistema de potencia, indican que esta no es analizada en las ecuaciones financieras. No obstante, establecen la correlación entre las potencias activas y la reactiva, por ello, se establece la necesidad que ambos rubros sean considerados en el precio.

Abinaya et ál. en 2014 [15] realiza un análisis de los costos de la potencia reactiva a partir del uso de la teoría de los costos marginales en mercados eléctricos, se explica la importancia de la potencia reactiva pues este tipo de potencia es necesario para el trasiego de potencia activa y mantener la seguridad operativa del SEP. Se hace un análisis a un sistema IEEE-14 y se propone un flujo de potencia a partir de un despacho óptimo de potencia reactiva.

Kumar y Kumar en 2015 [16] proponen la tarifa de la potencia reactiva en sistemas eléctricos de los mercados eléctricos abiertos, en este se cuantifica la potencia reactiva a partir de la curva de la capacidad del generador. Se plantean las funciones de costos marginales y se hace un desarrollo computacional a partir de una red de distribución de prueba IEEE-24 para minimizar el costo de la potencia reactiva. Los resultados son validados con otros métodos de estimación de costos, por último, se hace un análisis de los costos para potencia activa.

Teoría

Componentes de un Sistema Eléctrico

Un sistema eléctrico de potencia tiene varias componentes que constituyen las partes principales del mismo. Entre ellos están: Generación, Transmisión y Distribución. Cada una de ellas, serán parte vital a fin de garantizar el suministro eléctrico de los clientes y los usuarios de la electricidad. En la figura 1 se muestra un esquema de un sistema eléctrico.

La generación de electricidad puede darse por métodos convencionales y no convencionales, los primeros son de una manera clásica como la hidráulica, geotérmica y térmica. No obstante, debido al desarrollo de nuevas tecnologías hoy día se recurre a formas no convencionales como la energía eólica y solar, están van tomando un auge importante y su penetración hoy día es objeto de estudios en los sistemas eléctricos de potencia. La transmisión requiere de las líneas para el “transporte” de la energía a los centros de consumo y es llevada a las subestaciones donde se transforma en niveles permisibles y seguros para las personas y equipos.

Por esta razón variables como la tensión y la frecuencia son importantes en la regulación. Ambos elementos operan simultáneamente con la variable de tensión eléctrica y son fundamentales en la calidad del servicio prestado por las compañías eléctricas a los clientes de los servicios eléctricos. Por ejemplo, en Costa Rica se permite una variación de la tensión de ±5% y con respecto a la frecuencia eléctrica no puede variar en ±0.5% de acuerdo con lo establecido por el regulador de servicios públicos. [18].

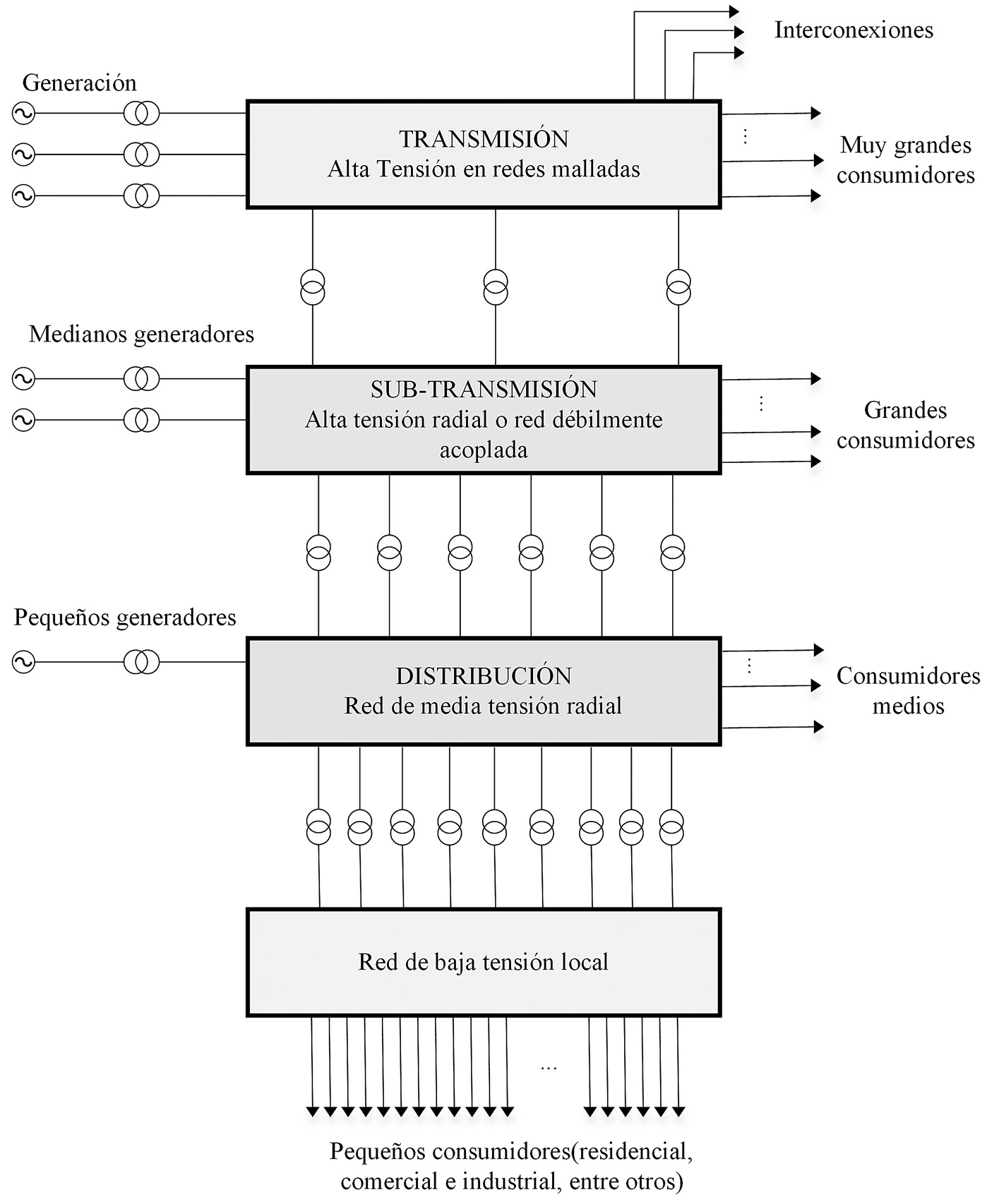
Figura 1. Esquema básico de Sistema Eléctrico de Potencia basado en Eremia y Shahidehpour [17]

Calculo del Flujo de Potencia entre líneas y otros elementos

El cálculo y análisis del flujo de potencias en la red eléctrica es uno de los aspectos más importantes de su comportamiento en régimen permanente pues consiste en determinar los flujos de potencia activa y reactiva en cada línea eléctrica del sistema y las tensiones en cada una de las barras. Existen distintos métodos para el cálculo del flujo de potencias, entre los que se pueden mencionar: Gauss, Newton-Raphson y Gauss-Seidel. [19] [20] El presente artículo se desarrolló por el método de Gauss Seidel.

Cálculo de Costos por Potencia Reactiva para bancos de capacitores y generadores sincrónicos

Para el caso del banco de capacitores, se propone la ecuación 1 para el cálculo de la potencia reactiva:

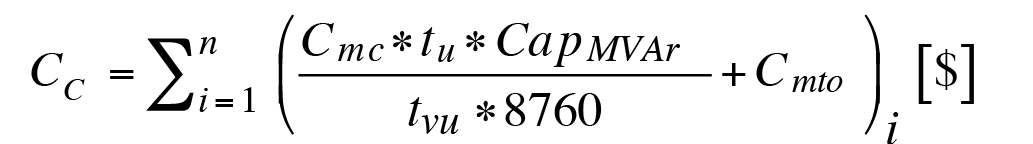(ec.1)

donde

Cic = Costo por entrega de potencia por medio de banco de capacitores ($/periodo)

Cmc = Costo total del módulo de banco de capacitores ($/periodo)

tu = tiempo de uso del banco de capacitores (Horas/periodo)

CapMVAr = capacidad del banco de capacitores (MVAr)

tvu = tiempo de vida útil del banco de capacitores (años)

8760: horas del año

Cmto: costo del mantenimiento ($/periodo)

i = número de barras del SEP

La principal limitante del banco de capacitores es que entregará toda la potencia para la cual está diseñado y este no tiene la capacidad de regulación de la potencia reactiva que inyecta al sistema eléctrico.

Cálculo del costo para compensador síncrono

Para el caso del compensador síncrono, se propone la ecuación 2 para calcular el costo para potencia reactiva despachada:

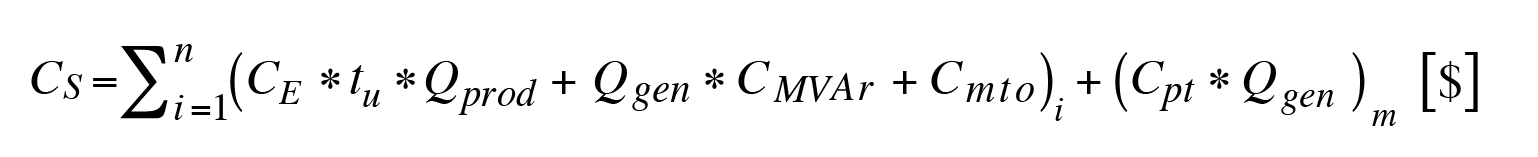(ec.2)

donde

Cim = Costo por producir Potencia Reactiva ($/periodo)

CE = Costo de Potencia Reactiva por hora ($/KVArH)

CMVAr = Costo Potencia ($/KVAr)

tu = Tiempo de utilización (Horas/periodo)

Qprod = Potencia Reactiva en función del tiempo entregada a la red (MVAr-H)

Qgen = Potencia Reactiva entregada a la red (MVAr/periodo)

Cmto: Costo del mantenimiento del periodo ($/periodo)

Cpt: Costo del peaje de transmisión ($/KVAr)

m=cantidad de líneas de transmisión del SEP

Los costos totales de la potencia reactiva debido a la inyección por los bancos de capacitores y el compensador síncrono deben ser calculados en la siguiente ecuación de costos en cada uno de los nodos del sistema eléctrico:

CT = CC + CS [$]

donde

CT: costos totales de potencia reactiva inyectada

CC: costos de potencia reactiva por bancos de capacitores

CS: costos de potencia reactiva por compensador síncrono

Ecuación de Optimización para establecer Función Objetivo

Una vez establecidos estos valores se debe plantear las variables para la función objetivo y de esta manera aplicar una técnica de optimización lineal, de acuerdo a lo indicado en el cuadro 1.

Cuadro 1. Variables para Función Objetivo

Elemento de compensación	Potencia entregada al SEP X [$]	Costos Totales por mantenimiento Y [$]	Costos por Peajes Z [$]
Banco de capacitores	A	B	N/A
Compensador síncrono	C	D	E

Las funciones objetivo para cada uno de los elementos son representadas por las siguientes ecuaciones:

• Banco de capacitores: min AX + BY

• Generador Síncrono: min CX + DY + EZ

• En caso que el nodo contenga banco de capacitores y generador síncrono se analiza de la siguiente manera: AX + BY +CX + DY + EZ

En estas ecuaciones el método de optimización lineal buscará despachar el máximo de potencia reactiva al más bajo costo. Previamente en los estudios de flujos de potencia se deberán obtener los perfiles máximos y mínimos de potencia reactiva, realizar un análisis de contingencia y evaluar la peor condición para el sistema en estudio. De esta manera, se sabrán las condiciones nominales y contingencia, con la finalidad de planificar el requerimiento de bancos de capacitores, compensadores síncronos y lo necesario para mantener el sistema en condiciones de operación normal.

Resultados

El SEP de prueba a utilizar es un IEEE-14 el cual posee 14 barras, 20 líneas de transmisión, 6 generadores síncronos, 9 cargas y 3 autotransformadores de interconexión. [21] La barra 1 es la de referencia y para el estudio de flujo de potencia las barras 2,3,6 y 8 son las barras P-V (Potencia-Tensión), necesarias para la regulación de estas variables en el sistema eléctrico. De igual manera, las restantes 9 barras tipo P-Q (Potencia Activa-Potencia Reactiva), las cuales representan los centros de consumo de la red eléctrica. Para el desarrollo de la metodología, por lo tanto, se deben seguir los siguientes pasos, de acuerdo a la figura 2.

Potencia Reactiva del sistema propuesto

Se realizó un análisis de contingencias únicas donde se obtuvieron los siguientes valores de potencia reactiva a fin de valorar los requerimientos de la potencia en cada una de las barras del sistema eléctrico tal y como se muestra en el cuadro 2.

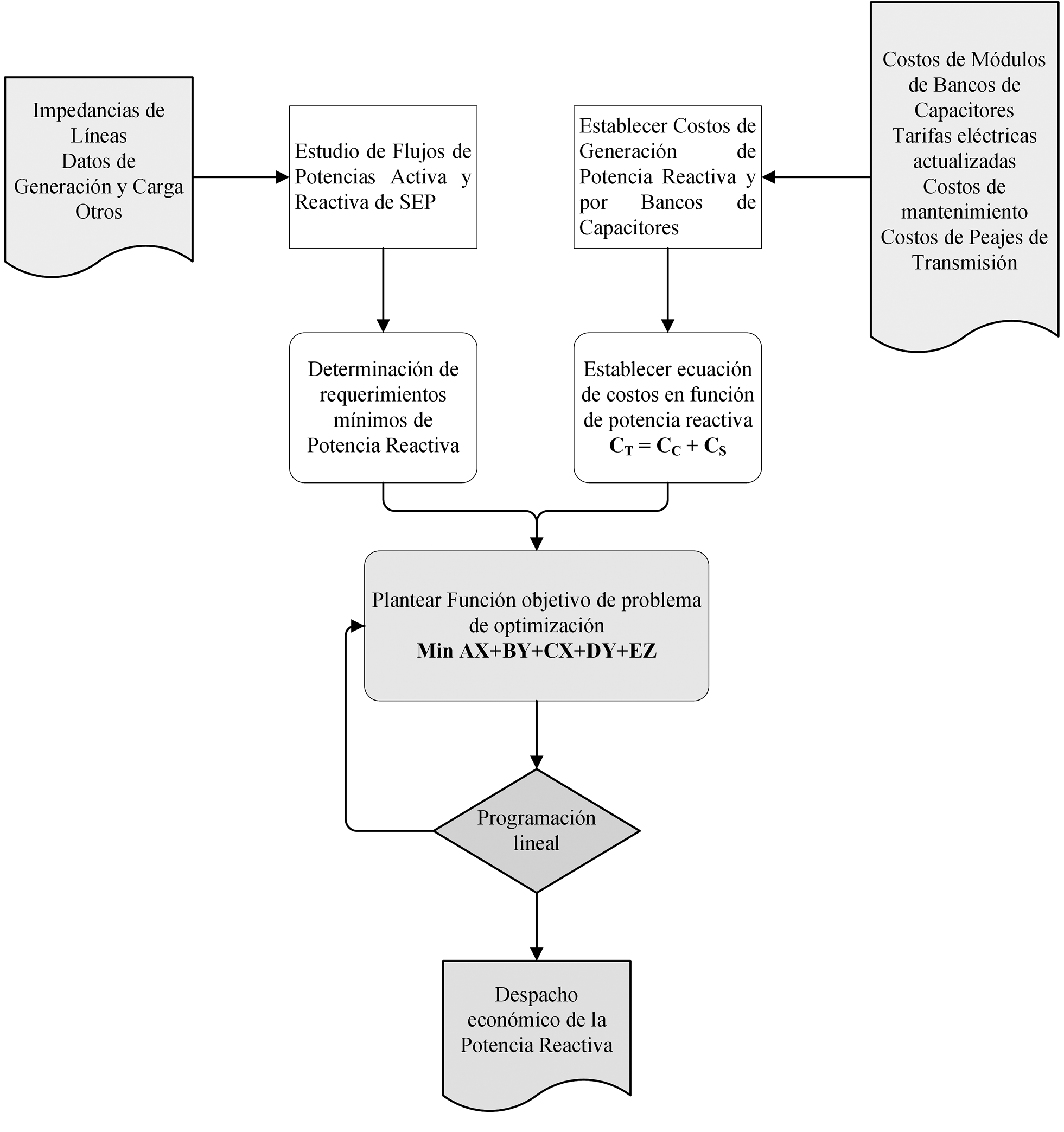
Figura 2. Flujograma de metodología para el cálculo óptimo de la potencia reactiva basado en datos de esta investigación.

Calculo de Potencia reactiva a partir de bancos de capacitores

Se obtienen los costos al utilizar bancos de capacitores en los nodos de interconexión, el costo aproximado de los módulos de compensación se puede obtener de la metodología de la remuneración de la actividad de transmisión de Colombia [22]. Tomando en consideración todos estos elementos se tiene los siguientes costos de potencia reactiva de acuerdo al cuadro 3.

Cuadro 2. Requerimiento de Potencia Reactiva en Barras del Sistema Propuesto.

Barra	Rangos de Potencia Reactiva [MVAr]		Requerimiento de Potencia Reactiva [MVAr]
	Qmax	Qmin
1	24,268	-2,855	27,123
2	17,490	-23,925	41,415
3	1,358	-20,867	22,225
4	8,379	-14,953	23,332
5	13,858	-8,621	22,479
6	8,599	-4,902	13,501
7	14,487	-24,912	39,399
8	26,620	-2,777	29,398
9	3,902	-9,773	13,675
10	3,962	-3,962	7,925
11	4,374	-4,513	8,887
12	1,478	-2,404	3,882
13	2,902	-7,893	10,795
14	2,496	-2,650	5,146

Cuadro 3. Costos de Potencia Reactiva a partir de bancos de capacitores.

Barra	Requerimiento de Potencia Reactiva (MVAr)	Cmc ($)	tu (horas)	tvu (años)	Costos de Mantenimiento Cmto	Costos por insertar Bancos de Capacitores ($)	Costo unitario de Potencia Reactiva $/(KVAr)
Barra 4	23,332	$3.427.673	420	7	$746	$548.516,3	23,509
Barra 5	22,4791	$3.427.673	420	7	$746	$528.492,6	23,510
Barra 7	39,3985	$3.427.673	420	7	$746	$925.712,9	23,496
Barra 9	13,6753	$3.427.673	420	7	$746	$321.803,9	23,532
Barra 10	7,9248	$3.427.673	420	7	$746	$186.798,2	23,571
Barra 11	8,8869	$3.427.673	420	7	$746	$209.385,6	23,561
Barra 12	3,8824	$3.427.673	420	7	$746	$91.893,9	23,669
Barra 13	10,7948	$3.427.673	420	7	$746	$254.177,8	23,546
Barra 14	5,1464	$3.427.673	420	7	$746	$121.569,1	23,622
				Total		$6.330.061,1

Cálculo de Potencia Reactiva a partir de generadores síncronos

De acuerdo con lo planteado en la ecuación anterior, se obtienen los costos al utilizar generadores sincrónicos en los nodos de interconexión. Tomando en consideración todos estos elementos se tiene los siguientes costos de potencia reactiva conforme a los planteado en el cuadro 4.

Cuadro 4. Costos de Potencia Reactiva a partir de generador sincrónico.

Barra	Requerimiento de Potencia Reactiva (MVAr)	Qgen (MVAr)	Qprod (MVAr/H)	CE ($/KWH)	tu (horas)	Cpt ($/MVA)	Cmto ($)	CMW ($/KW)	Datos Máquinas en MVA	Valor q	Límites de Generación		Costos por Generar Potencia Reactiva ($)	Costo Unitario de Potencia Reactiva $/KVAr
											Qmáx	Qmín
Barra 1	27,12	27,1228	85534462,1	$0,06	360	$0,1054	$746	$3,35	250	0,20	145		$1.027.160,44	$37,87
Barra 2	41,41	41,4146	130605083	$0,06	360	$0,1054	$746	$3,35	175	0,29	50	-40	$2.239.692,23	$54,08
Barra 3	22,22	22,2249	70088444,6	$0,06	360	$0,1054	$746	$3,35	90	0,44	40		$1.869.772,82	$84,13
Barra 6	13,50	13,5009	42576438,2	$0,06	360	$0,1054	$746	$3,35	120	0,20	24	-6	$511.663,71	$37,90
Barra 8	29,39	29,3975	92707956	$0,06	360	$0,1054	$746	$3,35	150	0,16	24	-6	$890.743,16	$30,30
												Total	$6.539.032,36

Costos Totales para SEP propuesto

El costo total mensual de $12 869 836.2 para despachar y operar el sistema eléctrico propuesto, en las condiciones indicadas anteriormente. De esta manera una vez establecido el costo total se procederá a aplicar la optimización del SEP con el fin de cumplir el requerimiento de potencia reactiva demandada al menor costo económico.

Despacho Óptimo de la Potencia Reactiva del SEP propuesto

De acuerdo con lo planteado anteriormente, se procede a desarrollar una programación lineal para el despacho óptimo de potencia reactiva al menor costo. En ella, la función objetivo tendrá las siguientes consideraciones en la programación:

a) Las barras 10,11,12,13 y 14, tendrán bancos de capacitores debido a la lejanía del centro de generación de cada una de las barras indicadas anteriormente. Los bancos de capacitores recomendados serán de 20 MVAr, similares a los que se usan en el SEN. La principal limitante de estos dispositivos es que entregan la totalidad de la potencia y no dan posibilidad de regulación a diferencia de los compensadores síncrono o generadores síncronos.

b) En la barra 1 se tendrá conectado un generador síncrono de gran capacidad que será capaz de entregar potencia reactiva hasta 145 MVAr. La importancia de este es que debido a su condición se utiliza para regulación del SEP y el regulador de tensión se deja en modo automático para que este supla el requerimiento del sistema de potencia reactiva ante los cambios que sucedan en la red.

c) En la barra 2 se tendrá conectado un generador que será capaz de entregar potencia reactiva desde un rango de 50 hasta -40 MVAr. El signo negativo es que podrá consumirla en caso de requerimiento de regulación del SEP. Esta es una condición normal de operación.

d) En barra 3 se tendrá conectado un compensador síncrono con capacidad de entregar hasta 40 MVAr.

e) En la barra 6 y 8 se tendrá conectado un compensador síncrono el cual será capaz de entregar potencia reactiva desde un rango de 24 hasta -6 MVAr. El signo negativo es que podrá consumirla en caso de requerimiento de regulación del SEP. Esta es una condición normal de operación.

f) El requerimiento de potencia reactiva máximo es de 269.18 MVAr, este valor no puede ser inferior pues existiría el riesgo de colapso parcial o total del sistema.

Análisis de Escenarios

A continuación, se hará un análisis de escenarios a fin de validar el modelo propuesto. Para ello se considerará una utilización del 60% en promedio de los bancos de capacitores, la vida útil será de 7 años, pues estos son elementos sensibles a los ciclos de trabajo que tengan a lo largo de su ciclo de utilización. Los costos calculados en los generadores sincrónicos en los nodos de interconexión 1, 2, 3, 6 y 8 se muestran a continuación, se tomaron en cuenta un tiempo de uso de 360 horas de las 720 que puede tener un mes, esto representa una utilización del 50% aproximadamente de la típica de estos elementos al mes.

De acuerdo con lo planteado anteriormente, se procede a desarrollar una programación lineal para el despacho óptimo de la potencia reactiva, la función objetivo tendrá las siguientes condiciones en la programación:

i. Las barras 10, 11, 12, 13 y 14 tendrán bancos de capacitores debido a la lejanía del centro de generación de cada una de las barras indicadas anteriormente. Los bancos de capacitores recomendados serán de 20 MVAr.

ii. En la barra 1 se tendrá conectado un generador síncrono 145 MVAr.

iii. En la barra 2 se tendrá conectado un generador que será capaz de entregar la potencia reactiva, desde un rango de 50 hasta -40 MVAr.

iv. En la barra 3 se tendrá conectado un compensador síncrono con capacidad de entregar hasta 40 MVAr.

vi. En la barra 6 y 8 se tendrá conectado un compensador síncrono el cual será capaz de entregar la potencia reactiva, desde un rango de 24 hasta -6 MVAr.

El requerimiento de potencia reactiva máximo es de 269.18 MVAr, este valor no puede ser inferior pues existiría el riesgo de colapso parcial o total del sistema de acuerdo al estudio de flujos de potencia.

El requerimiento de potencia reactiva para el sistema eléctrico planteado es 269.18 MVAr y un costo base inicial obtenido en el cuadro 3 de $12 869 093.50. En el escenario pesimista considera una utilización de 60 MVAr de los bancos de capacitores y un despacho mínimo de la generación en barra 1 de 72 MVAr, por esta razón el costo total obtenido en la programación lineal es $11 778 813.10, con un ahorro del 8.47%.

En escenario realista considera una utilización de 80 MVAr y un despacho máximo de la unidad de la generación en la barra 1 de 112 MVAr. Por esta razón el costo total obtenido de la programación lineal es $9 344 862.60, con un ahorro del 27.39 %.

En escenario optimista considera una utilización de 100 MVAr y un despacho máximo de la unidad de la generación en la barra 1 de 145 MVAr. Por esta razón costo total obtenido es de $8 584 718.95, con un ahorro del 33.39 %. En la siguiente grafica de resultados se puede observar el comportamiento de los escenarios planteados de acuerdo con las condiciones y requerimientos del sistema de potencia. En la figura 3 se observa el comportamiento de los escenarios ante las condiciones propuestas.

Figura 3. Comparación de Escenarios para el despacho de Potencia Reactiva para SEP propuesto basado en datos de esta investigación.

Discusión Final

Se logró desarrollar una propuesta de metodología capaz de hacer un despacho óptimo de esta potencia al menor costo. Por ello, se logró identificar los costos más importantes y relevantes, para posteriormente desarrollar una programación lineal a partir de una hoja electrónica en Microsoft Excel. Se logró proponer una metodología para el cobro de potencia reactiva y en ella, a partir de los datos del estudio de flujos de potencia, los costos de producir potencia reactiva, se plantea la función objetivo para resolver el problema de despacho económico [23]. En la parte B de la investigación se establecerá un modelo para el cobro diferenciado de las tarifas y de esta manera lograr proponer costos más bajos de la electricidad.

Agradecimientos

Agradezco a la Escuela de Ciencias de la Administración y al Posgrado en Administración de Negocios de la UNED por las herramientas y conocimientos gerenciales adquiridos para realizar este proyecto de investigación.

Lista de Abreviaturas

ARESEP: Autoridad Reguladora de los Servicios Públicos

MER: Mercado Eléctrico Regional

SEN: Sistema Eléctrico Nacional

SEP: Sistema Eléctrico de Potencia

KVAr: kilo Voltio Amperios reactivos

kVArH: kilo Voltio Amperios reactivos-hora

IEEE-14: Sistema Eléctrico de Potencia de prueba de 14 barras

Referencias

[1] C. Hsu and M.-S. Chen, “Reactive Power Planning and Operation in the Deregulated Power Utilities,” in Electricity Utility Deregulation and Restructuring and Power Tecnologies 2000, London, England, 2000.

[2] F. J. D. Miller, “Método de asignación de peajes de los sistemas de transmisión eléctrica según el uso de la red.,” Pontificia Universidad Católica de Chile, Santiago, 2001.

[3] V. M. Doña and A. N. Paredes, “Reactive power pricing in competitive electric markets using the transmisión losses function,” in 2001 IEEE Porto Power Tech Conference, Porto, Purtugal, 2001.

[4] J. H. Tovar Hernández, M. Jiménez Jiménez and G. Gutiérrez Alcaraz, “Metodología basada en Sensibilidad para Asignar Costos de los Servicios de Control de Voltaje y Potencia Reactiva en Mercados Eléctricos Desregulados,” Computación y Sistemas, pp. 58-66, 2002.

[5] G. C. Tequitlapa Gómez, “Asignación de cargos por servicios de control de voltaje y reservas reactivas en mercados de energía.,” Instituto Tecnológico de Morelia, Morelia, 2002.

[6] J. Zhong and K. Bhattacharya, “Reactive Power management in Deregulated Electricity Markets - A Review,” IEEE, pp. 1287-1292, 2002.

[7] R. V. Laguna, “Asignación de cargos por el porteo de flujos de potencia activa y reactiva en los sistemas de transmisión basada en el método del rastreo de la electricidad,” CINVESTAV, Gualadajara, 2002.

[8] V. B. Cortez Silva, “Señal de precios para la potencia reactiva en mercados descentralizados y competitivos.,” Pontificia Universidad Católica de Chile, Santiago, 2003.

[9] J. I. S. Macías and P. C. Pérez, “Regulación de las tarifas de acceso a las redes y liberación del sector eléctrico español,” Revista de Economía pública, pp. 61-83, 2003.

[10] S. B. Barrangán Gómez and J. Robles García, “Costo por el soporte de voltaje de los generadores en,” Científica, pp. 113-117, 2006.

[11] A. Carbajo, “Los mercados eléctricos y los servicios de ajuste del sistema,” Red Elétrica de España, pp. 55-62, 2007.

[12] H. S. Oh and R. J. Thomas, “Real and Reactive Power Prices and Market Power,” IEEE, 2007.

[13] H. R. R. Valenzuela, “Efectos económicos que conlleva la prestación del servicio de regulación de voltaje, por un agente generador asociado al sistema nacional interconectado,” Universidad de San Carlos, Guatemala, 2008.

[14] A. Rabiee, H. Ali Shayanfar and N. Amjady, “Reactive power pricing. Problems & a proposal for a competitive market,” IEEE power & energy magazine, pp. 18-32, 2009.

[15] K. Abinaya, D. Danalakshmi and S. Kannan, “Cost Analysis of Reactive Power Using Marginal Cost Theory in Electricity Markets,” 2014 International Conference on Circuit, Power and Computing Technologies, pp. 79-83, 2014.

[16] R. Kumar and A. Kumar, “Real and Reactive Power Price of Generators to Load in Pool Based Electricity Market Model,” in Energy Economics and Environment (ICEEE), 2015 International Conference on, Noida, India, 2015.

[17] M. Eremia and M. Shahidehpour, Handbook of Electrical Power System Dynamics, Piscataway, NJ: IEEE Press, 2013.

[18] ARESEP, AR-NT-POASEN-2015, San José, 2016.

[19] G. W. Stagg and A. H. El-Abiad, Computer Methods in Power System Analysis, Tokyo: McGraw-Hill, 1983.

[20] B. Stott, “Review of Load Flow Calculation Methods,” Proceedings of IEEE, pp. 916-929, 1974.

[21] University of Washington, “https://www2.ee.washington.edu/research/pstca/pf14/pg_tca14bus.htm,” 10 abril 2018. [Online]. Available: https://www2.ee.washington.edu/research/pstca/.

[22] Comisión de Regulación de Energía y Gas, “Metodología para la remuneración de la actividad de transmisión de energía eléctrica en el sistema interconectado nacional,” CREG, Bogota, 2016.

[23] M. Eremia and S. Nilsson, “Series Capacitive Compensation,” in Advanced Solutions in Power Systems: HVDC, FACTS, and Artificial Intelligence, New York, John Wiley & Sons, Inc, 2016, pp. 339-407.

[24] A. Gómez Expósito, J. L. Matínez Ramos, J. A. Rosendo Macías, E. Romero Ramos and J. M. Riquelme Santos, Sistemas Eléctricos de Potencia, Madrid: PEARSON, 2003.

[25] ARESEP, “https://app.powerbi.com/view?r=eyJrIjoiY2I2YTM1MzEtYzlmYS00NmE1LWFlM2QtYWM2YTYzYTEzMmFlIiwidCI6IjBkNzIzOGY4LWI3ODQtNDk2MC1iZGUyLTZlMzM1MWQyNDcwZCIsImMiOjR9,” 12 abril 2018. [Online]. Available: www.aresep.go.cr.

[26] ARESEP, Ley que Autoriza la Gneración Eléctrica Autónoma o Paralela, San José, 1995.

[27] ARESEP, Reglamento Sectorial de Sectores Eléctricos, San José, 2001.

---