Modelación de una antorcha de plasma de arco no transferido

Modeling of a non-transferred arc plasma torch

Bruno Chinè-Polito1, Manuel Mata-Coto2, Ivan Vargas-Blanco3

Fecha de recepción: 25 de abril de 2018
Fecha de aprobación: 3 de julio de 2018

Chinè-Polito, B; Mata-Coto, M; Vargas-Blanco, I. Modelación de una antorcha de plasma de arco no transferido. Tecnología en Marcha. Vol. 32-1. Enero-Marzo 2019. Pág 12-24.

DOI: https://doi.org/10.18845/tm.v32i1.4115

Palabras clave

Plasma; antorcha de arco no trasferido; modelación; métodos computacionales.

Resumen

Las antorchas de plasma se usan para producir el plasma en la manufactura de materiales e industria energética, donde las antorchas de arco de corriente directa representan los componentes principales de los procesos con plasma térmico (plasma spraying, soldadura, corte de metales, tratamiento de residuos, producción de biogás, etc.). En una antorcha de plasma de arco no trasferido, se desarrolla un arco eléctrico aplicando una corriente directa entre el cátodo y el ánodo de la antorcha. Sucesivamente, el plasma se produce calentando, ionizando y expandiendo un gas alimentado a la antorcha antes de la región del cátodo. Los trabajos de laboratorio que usan técnicas de observación y de medición son de difícil aplicación, debido a las características físicas de estos fenómenos físicos. Así las técnicas computacionales pueden representar una herramienta valiosa para investigar los procesos con plasma, aunque el trabajo computacional es extremadamente desafiante, pues estos fenómenos son interdependientes y simultáneos. En este trabajo se propone un modelo computacional para simular una antorcha de plasma bidimensional de arco no trasferido en equilibrio termodinámico local. Se modelan condiciones de estado estacionario para las ecuaciones de conservación de mecánica de fluidos, trasferencia de calor y electromagnetismo en el software Comsol Multiphysics® 5.1. En la trasferencia de calor por radiación, el plasma se asume ópticamente fino y con un coeficiente de emisión neta. El flujo laminar de gas se modela con vórtice libre en la entrada para dos tipologías de antorchas axis-simétricas, respectivamente con argón y nitrógeno como gases de trabajo.

Keywords

Plasma; non-transferred arc torch; modelling; computational methods.

Abstract

Plasma torches are used in processing of materials and in energy industry for producing plasma, where direct currents arc torches represent the primary components of thermal plasma processes (plasma spraying, metal welding and cutting, waste treatment, biogas production, etc.). In a non-transferred arc plasma torch, an electric arc can be glowed by applying a direct current between the cathode and anode, both placed inside the torch. Then, the plasma is obtained by heating, ionizing and expanding a working gas, introduced into the chamber of the torch upstream of the cathode. Experimental works carried out by observation and measurements techniques are difficult to apply in this field, owing to the specific properties of these physical phenomena. Hence, computational techniques could represent a useful tool to investigate the plasma processing, although the computational work is extremely challenging, because the physical phenomena are not independent among them and simultaneous. In this work we provide a computational model for simulating a 2D non- transferred arc plasma torch, under hypothesis of local thermodynamic equilibrium. Steady state conditions are assumed for the equations of conservation of fluid mechanics, heat transfer and electromagnetics which are modeled by the Comsol Multiphysics® 5.1 software. The plasma is considered optically thin and a net emission coefficient is used for the heat transferred by radiation mechanisms. The gas flow is modeled as laminar with a free vortex at the inlet for two kinds of axisymmetric torches, one with argon and the second one with nitrogen as working gas, respectively.

Introducción

El plasma consiste de una mezcla de electrones, iones y partículas neutras. Las tecnologías de plasma recurren a la creación de un arco eléctrico a través de un gas que, por su resistividad eléctrica, genera altos valores de energía térmica permitiendo separar los electrones de sus átomos y moléculas y originando un gas ionizado o plasma. A temperaturas superiores a 2000 °C las moléculas del gas son disociadas en átomos y para valores mayores a 3000 °C, los átomos pierden electrones y llegan a estar ionizados [1]. El plasma térmico, es decir el gas ionizado donde las temperaturas de los electrones y de los iones son iguales, presenta altos valores de temperatura, emite radiación no ionizante y brinda una alta densidad de energía. Sus propiedades permiten que tenga múltiples aplicaciones en la industria (plasma spraying, soldadura, corte plasma, etc.), mientras que el actual aumento en las cantidades de desechos sólidos alrededor del mundo favorece la introducción de las tecnologías de plasma para su tratamiento industrial y posterior eliminación [2,3].

Los plasmas térmicos, tal como los utilizados en el tratamiento de residuos, pueden ser generados por muchos métodos incluyendo descargas eléctricas de corriente directa (DC) o de corriente alterna (CA), arcos transitorios (lámparas o arcos de pulso), descargas de radio frecuencia y microondas y los plasmas inducidos por láser. Los métodos de producción de plasma incluyen las antorchas de plasma DC como componentes principales del proceso [4]. En este caso las antorchas constituyen una parte esencial de los reactores de gasificación, donde el plasma es generado y confinado en una pequeña cavidad con geometría cilindro-cónica. Las tecnologías en uso prevén que se desarrollen descargas eléctricas de alta temperatura en el interior de la misma antorcha, entre un elemento central (cátodo) y la superficie interna de la pared de la antorcha (ánodo), como para las antorchas de arco no transferido [5]. Sucesivamente, en el arco eléctrico creado trasversalmente a la dirección del flujo del gas alimentado a la antorcha, se genera el plasma que luego se expande entre los mismos electrodos, adquiriendo la forma de un chorro de alta temperatura (plasma jet).

Las antorchas DC de plasmas de arco térmico se construyen con ánodos de cobre que deben ser refrigerados para aumentar su vida útil. El cátodo se fabrica con cobre en las antorchas de cátodo frío, mientras se utilizan cátodos de tungsteno con punta de torio en las antorchas de cátodo caliente. Dependiendo de la aplicación, pueden utilizarse distintos gases en la alimentación de la antorcha, como aire, argón, nitrógeno, dióxido de carbono e inclusive vapor de agua. En literatura (ver por ejemplo [6,7]) se pueden revisar otros aspectos sobre tipologías, materiales y características de las antorchas.

La modelación de una antorcha DC de plasma debe considerar muchos mecanismos, por la presencia de diferentes especies y diversos fenómenos físicos acoplados. Debido a la interacción entre los campos eléctrico, magnético, térmico y de velocidad, el régimen de flujo del plasma en la antorcha es altamente no lineal, con presencia de fuertes gradientes y efectos termodinámicos y químicos de no equilibrio. Trelles et al. [8] presentan los fundamentos de la modelación del arco del plasma y revisan los mecanismos principales. Bajo hipótesis de equilibrio termodinámico local (LTE), las temperaturas de los electrones y de las partículas pesadas son aproximadamente iguales y el plasma se puede modelar usando las ecuaciones de la magneto-hidrodinámica (MHD). La aproximación LTE no es válida cerca de las fronteras del plasma en la antorcha, donde el gas puede interactuar con paredes solidas frías o con corrientes de gas frio. Siendo que las propiedades del plasma dependen fuertemente de la temperatura, se puede originar una desviación importante respecto del comportamiento real del plasma, cuando la temperatura de los electrones se asume ser igual a la de las especies pesadas [8]. Por ejemplo, un aspecto peculiar está representado por la baja conductividad eléctrica σ del plasma para temperaturas T inferiores a un valor critico (para gas argón σ ≤ 1 S/m si T< 4600 K).
Consecuentemente, cerca de las paredes refrigeradas del ánodo de la antorcha, no se puede garantizar la descarga de corriente eléctrica usando modelos de LTE. Para superar esta dificultad, se han usado valores artificiales de σ en las regiones cercanas a las paredes del ánodo [8, 9], estimando la posición de la base del arco eléctrico sobre el ánodo y la forma misma del arco [9] y para la dinámica de la misma base en estudios transitorios [8]. Otra alternativa es considerar la aplicación del concepto de producción de entropía mínima para determinar la dimensión real del radio del arco y su longitud [10]. Para reducir la complejidad del trabajo de modelación, se han desarrollados modelos computacionales estacionarios en geometrías bi- y tri-dimensional y también axis-simétricos bidimensionales, que en algunos casos pueden originar resultados no realísticos [9]. Usando un software comercial, Deng et al. [11] proponen un modelo MHD para simular el campo electromagnético, la transferencia de calor y el flujo del plasma en una antorcha DC, bajo condiciones de régimen laminar y turbulento. El sitio de la base del arco se computa automáticamente, siendo igual a la posición del valor máximo de la densidad de corriente en la superficie interior del ánodo. Finalmente, Mendoza et al. [12] modelan un plasma térmico de tipo DC en un dominio tri-dimensional y calculan el sitio de la base del arco.

En las secciones sucesivas del artículo se describe el trabajo de modelación, que tiene la siguiente estructura: la descripción del modelo físico y matemático se brinda en el párrafo 2; en la sección 3 se reporta el modelo computacional desarrollado con el software Comsol Multiphysics®; seguidamente en la sección 4 se analizan los resultados numéricos obtenidos y en el párrafo 5 se presentan las conclusiones del trabajo.

Modelación físico-matemática de la antorcha de corriente directa

Modelo físico: dimensiones de la antorcha y materiales

Con el propósito de poder comparar nuestros resultados con datos de la literatura científica, se seleccionan dos tipologías de antorchas, la antorcha 1 estudiada computacionalmente por He-Ping Li et al (He-Ping Li et al. [9], He-Ping Li and Xi Chen [13]) y la antorcha 2 usada por Mozingo en su actividad experimental [14]. Usando condiciones de axis-simetría, ambas antorchas DC de plasma se pueden modelar como una región bidimensional [15]. En las figuras 1 y 2 se brindan respectivamente las dimensiones de las antorcha 1 y 2, con el sistema de coordenadas cilíndricas r,z, usado para la modelación del plasma. Los gases de trabajo son argón para la antorcha 1 y nitrógeno para la antorcha 2, mientras el material del ánodo y del cátodo es cobre para ambas antorchas. Todas las propiedades físicas de los materiales se obtienen de la base de datos de Comsol Multiphysics® 5.1. En el modelo se consideran condiciones de equilibrio termodinámico local (LTE), luego las temperaturas de los electrones y de las partículas pesadas son iguales. En este caso un aspecto peculiar es la baja conductividad eléctrica σ para temperaturas T por debajo de un valor crítico: para gas argón σ ≤ 1 S/m si T< 4600 K, mientras que para gas nitrógeno σ ≤ 1 S/m si T< 5300 K, aproximadamente. Para asegurar el flujo eléctrico se usa un valor artificial mínimo de 8000 S/m (σmin) para las conductividades eléctricas de los gases argón y nitrógeno. Debido al régimen estacionario, la dinámica del arco sobre la superficie del ánodo no se modela. Para los fenómenos de radiación térmica el plasma se considera ópticamente fino, usando un coeficiente de emisión térmica neto. Además, se asume un flujo gaseoso laminar y débilmente compresible, valido para un numero de Mach menor a 0.3. Con el propósito de definir condiciones de flujo rotacional en la entrada de la antorchas, se modelan regimenes de vórtices libre, siendo la velocidad azimutal vq inversamente proporcional a r.

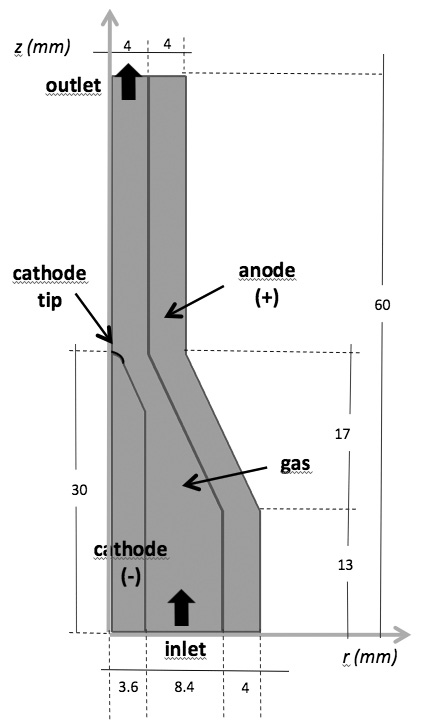
Figura 1. Geometría 2D de la antorcha 1 de He-Ping Li et al. [9].

Figura 2. Geometría 2D de la antorcha 2 de Mozingo [14].

Modelo matemático: ecuaciones diferenciales de conservación

En condiciones de flujo laminar y débilmente compresible del gas de la antorcha, las ecuaciones diferenciales en estado estacionario de continuidad y de conservación del momentum de Navier-Stokes en notación tensorial, son las siguientes [16]:

(2.1)

(2.2)

donde las magnitudes ρ, η y u son respectivamente la densidad, la viscosidad dinámica y la velocidad del fluido, p la presión, I el tensor identidad y F las fuerzas de cuerpo, incluyendo la fuerza de Lorentz FL. Por otro lado la conservación de la energía térmica en la antorcha se describe mediante la siguiente ecuación de Fourier que incluye las magnitudes de transporte convectivo y los términos fuente [17]:

(2.3)

donde T representa la temperatura, siendo k, Cp y Q respectivamente la conductividad térmica, el calor especifico a presión constante y los términos fuentes. La magnitud Q modela el calentamiento Joule QJ, la perdida volumétrica neta de energía por radiación (definida mediante el coeficiente de emisión neta) y el transporte de entalpia. Para los fenómenos electromagnéticos estacionarios en la antorcha de plasma, se introduce el potencial magnético vectorial A y el potencial eléctrico escalar V, mediante las ecuaciones:

(2.4)

(2.5)

con B que representa la densidad de flujo magnético y E la intensidad de campo eléctrico. Consecuentemente, las ecuaciones de Maxwell:

(2.6)

(2.7)

(2.8)

(2.9)

y la conservación de la carga:

(2.10)

se formulan en términos de estos potenciales [18]. En estas relaciones, la cantidad describe la densidad de corriente, representa la intensidad del campo magnético y la densidad del flujo eléctrico. Nuevamente u es el campo de velocidad del medio electromagnético, mientras que la propiedades σ, μ y ε son respectivamente la conductividad eléctrica, la permeabilidad magnética y la permisividad eléctrica del medio. Adicionalmente, para completar el acople del modelo termo-fluido-electromagnético de la antorcha de plasma, las magnitudes FL y QJ se expresan en términos de las variables electromagnéticas J, E y B, usando las definiciones siguientes:

(2.11)

(2.12)

Las ecuaciones 2.1 hasta 2.12 constituyen el sistema de ecuaciones diferenciales del modelo de la antorcha de plasma de arco térmico no transferido, para las cuales deben definirse las condiciones de borde, con el propósito de obtener la solución numérica. Las condiciones de borde implementadas se presentan en la próxima sección, conjuntamente con la descripción del modelo computacional desarrollado con el software COMSOL Multiphysics® 5.1.

Modelo computacional en Comsol Multiphysics®

En esta sección se describe el trabajo de modelación realizado con COMSOL Multiphysics® 5.1, un software comercial que emplea el método de elementos finitos para calcular numéricamente la solución de las ecuaciones diferenciales con derivadas parciales, obtenidas modelando los diversos procesos físicos de la antorcha. El modelo axis-simétrico de la antorcha de plasma con corriente directa se implementa en el software usando las librerías de las físicas de los módulos CFD [16], Heat Transfer [17], AC/DC [18] y Plasma [19], este último para los fenómenos del acoplamiento del flujo multifísico de la antorcha de plasma.

Condiciones de frontera implementadas

Para las condiciones de frontera de la ecuación diferencial de Fourier de la conservación de la energía térmica, se asumen en la antorcha: una temperatura de 300 K en la entrada; un ánodo enfriado externamente (con un coeficiente de transferencia h igual a 104 W/(m2 K) y una temperatura externa Text de 500 K) e internamente una transferencia de energía por radiación de cuerpo gris; una temperatura de 3500 K (emisión termoiónica) en la punta del cátodo; transferencia de calor por radiación sobre las paredes del cátodo considerado como cuerpo gris; aislamiento térmico en las otras superficies de la antorcha mediante la ecuación , donde q representa el flujo de calor y n la dirección normal a la superficie.

Para la evolución del campo de velocidad de las ecuaciones de Navier-Stokes, se fija en la entrada de la antorcha un flujo volumétrico G de argón de 2.0 STP m3/h para la antorcha 1 de He-Ping Li [9, 13], dando una velocidad axial vz de 1.35 m/s. Definiendo la velocidad azimutal vq del vórtice libre como vq = k1 /r, se consideran los siguientes tres valores de k1: 4.86x10(-3) m2/s, 9.72x10(-3) m2/s y 14.58x10(-3) m2/s. Para la antorcha 2 de Mozingo [14], se asume en la entrada un flujo másico de nitrógeno igual a 2.17 g/s, equivalente aproximadamente a 6.35 STP m3/h y a una velocidad axial de 1.37 m/s. Nuevamente se modelan tres condiciones de flujo con vórtice en la entrada, con k1 igual a 0.291x10(-1) m2/s, 0.582x10(-1) m2/s y 0.873x10(-1) m2/s, respectivamente. Para las dos antorchas DC se fija una velocidad radial vr nula en la entrada. Finalmente, las otras condiciones de borde usuales son la de no deslizamiento en las paredes y presión nula en la salida de la antorcha de plasma.

Por otro lado, para resolver las ecuaciones de Maxwell en términos de los campos potencial eléctrico escalar V y potencial magnético vectorial A, se implementan los siguientes valores en las fronteras de la antorcha de plasma DC: en la punta redondeada del cátodo una densidad de corriente Jn con valores en el rango 107 ÷ 108 A/m2, equivalente a una intensidad de corriente I de 43.36÷433.6 A para la antorcha 1; una densidad de corriente en el rango de 106 ÷ 107 A/m2, que significa una intensidad de corriente I de 50.38÷503.8 A para la antorcha 2; la condición de aislamiento eléctrico sobre las restantes superficies del cátodo, en la entrada y en la salida de la antorcha; condición de potencial eléctrico nulo en la superficie interior del ánodo; aislamiento magnético en todos las fronteras, con el potencial magnético A que satisface la condición . Adicionalmente, se usa la condición gauge fixing Y0 = 1 A/m para el computo del potencial magnético vectorial A.

En último, en todas las ecuaciones del modelo computacional se usa la condición de simetría axial con respecto al eje z de la antorcha de plasma.

Resolución numérica de las ecuaciones del modelo

El sistema de ecuaciones diferenciales con derivadas parciales del modelo computacional se resuelve numéricamente en Comsol Multiphysics® 5.1, dividiendo la región bi-dimensional de la antorcha en tres dominios, cátodo, fluido (plasma) y ánodo. En el modelo los campos eléctrico y magnético se calculan en el fluido y en el ánodo, el flujo del fluido se simula solamente en la región del plasma, mientras que el transporte de energía térmica se implementan en todas las regiones. El dominio computacional se crea con un mallado que usa un poco más que 105 elementos triangulares para ambas antorchas, refinando la malla en las regiones del plasma y en proximidad de las paredes de los electrodos, lo cual resulta en un número de grados de libertad mayor que 106. Debido a que los fenómenos que gobiernan el plasma son altamente no lineales y simultáneos, se selecciona un método de resolución numérica completamente acoplado. Se usa el solucionador numérico directo MUMPS para la integración de las ecuaciones diferenciales y se implementa un estudio de barrido paramétrico del término de fuente de calor para mejorar y garantizar la convergencia de los cálculos. Para las diferentes corridas, el tiempo de solución es en media de 34600 s.

Resultados computacionales de las antorchas de corriente directa

Para la antorcha 1, usando un valor mínimo σmin of 8000 S/m en la región de argón, una intensidad de corriente de 0.8x108 A/m2 en la punta del cátodo y un flujo de vórtice libre en la entrada con k1 = 4.86x10(-3) m2/s, las figuras 3 y 4 muestran los campos de temperatura y velocidad, respectivamente. Estos campos se brindan en figuras 5 y 6 para la antorcha 2, con el mismo valor de σmin en la región de nitrógeno, k1= 0.291x10(-1) m2/s y Jn= 0.7x107 A/m2. En el caso la antorcha 1, la posición de la base del arco predicha por He-Ping y Xi Chen [13], es cerca de la intersección de la parte convergente y la parte cilíndrica del ánodo (z=30 mm) y no es uniforme en la dirección circunferencial. La misma posición se obtiene en las simulaciones computacionales del este trabajo, como evidencian los gráficos de figura 7 para la antorcha 1 (z=30 mm) y de figura 8 para la antorcha 2, donde se brinda la densidad de corriente normal a la pared del ánodo. En estas figuras, la densidad de corriente máxima corresponde a la base del arco en la pared interior del ánodo, que para ambas antorchas se computa exactamente en la intersección entre la sección cónica y la sección cilíndrica superior (z=30 mm para la antorcha 1 y z=85.25 mm para la antorcha 2). Sucesivamente se llevan a cabo nuevas simulaciones con el propósito de evaluar la variación del sitio de la base del arco en la pared del ánodo. En este caso se implementa un valor artificial σmin solamente en una región estrecha entre el cátodo y el ánodo, pudiéndose así investigar la influencia de conductividad eléctrica del gas sobre los resultados computacionales. He-Ping Li et al. [9] aplican el principio de Steenbeck y calculan la base del arco a una distancia de z=36 mm para la misma antorcha 1, usando una corriente de 400 A y un flujo volumétrico de gas argón 2.0 STP m3/h. De acuerdo a estos resultados, se modela una área estrecha de plasma en correspondencia de z=36 mm, entre la región central de la antorcha y la pared del ánodo, con la condición de σmin= 8000 S/m. Lo anterior equivale a fijar la posición de la base del arco, como confirma el valor de la densidad de corriente del gráfico de figura 9. En la simulación, la densidad de corriente normal en la pared interior del ánodo de la antorcha 1 ha sido evaluada para G = 2.0 STP m3/h, k1 = 4.86x10(-3) m2/s y Jn= 0.4x108 A/m2 (I=173.4 A).

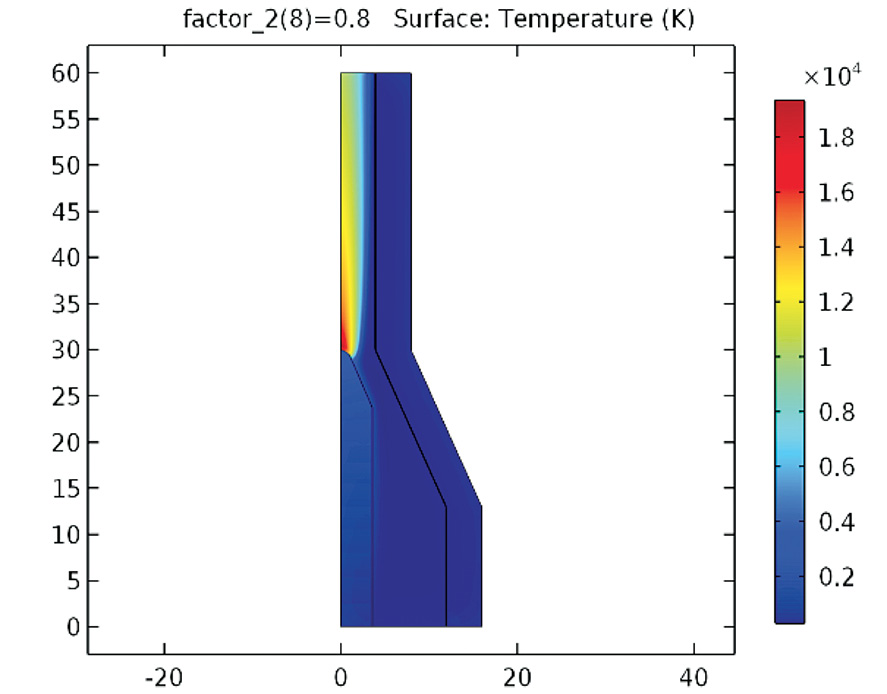
Figura 3. Campo de temperatura de la antorcha 1 (G = 2.0 STP m3/h, k1 = 4.86x10(-3) m2/s, Jn= 0.8x108 A/m2).

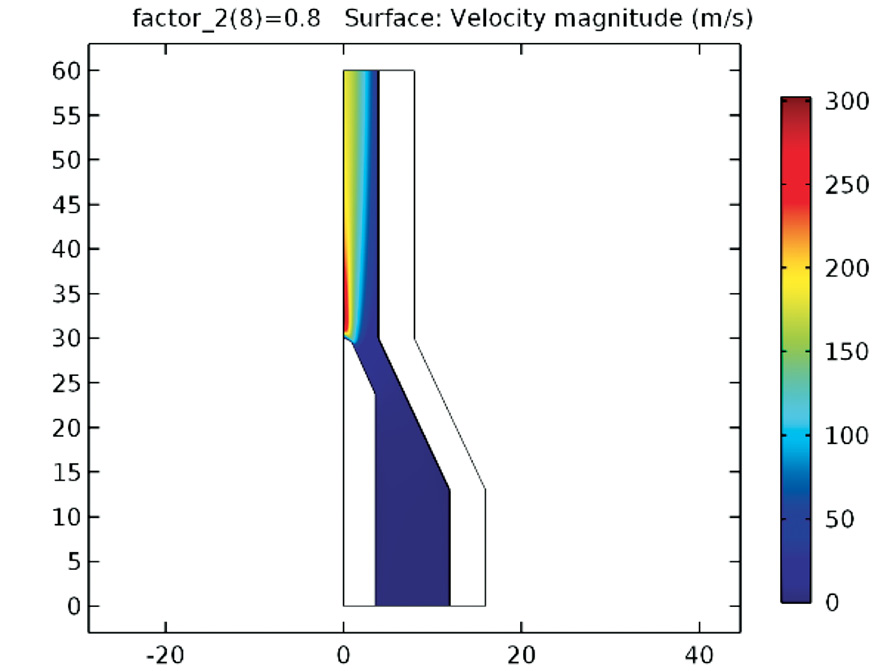
Figura 4. Campo de velocidad de la antorcha 1 (G = 2.0 STP m3/h, k1 = 4.86x10(-3) m2/s, 0.8x108 A/m2).

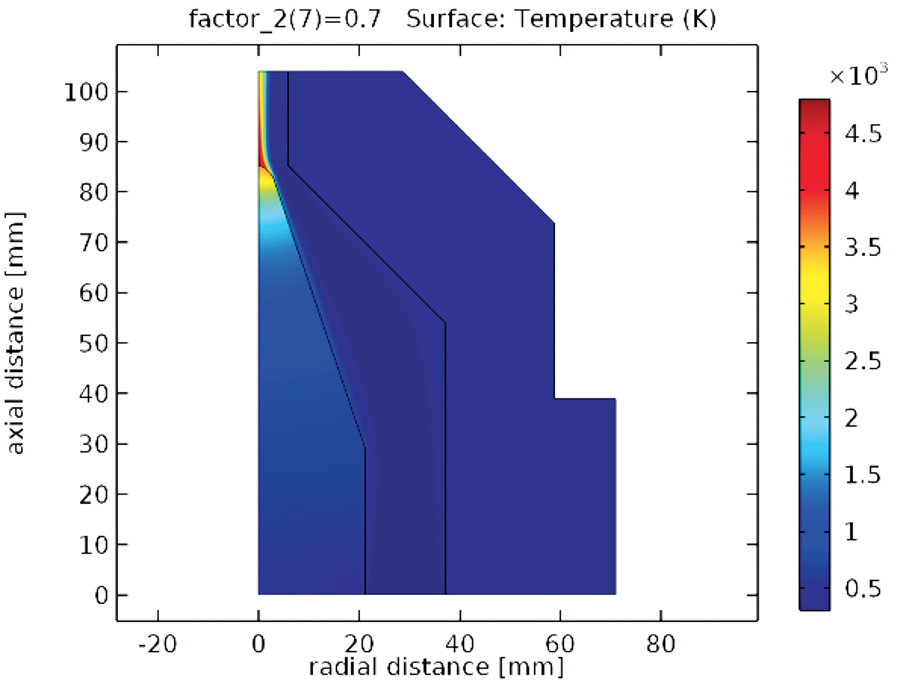
Figura 5. Campo de temperatura de la antorcha 2 (G = 6.35 STP m3/h, k1 = 0.291x10(-1) m2/s, Jn= 0.7x107 A/m2).

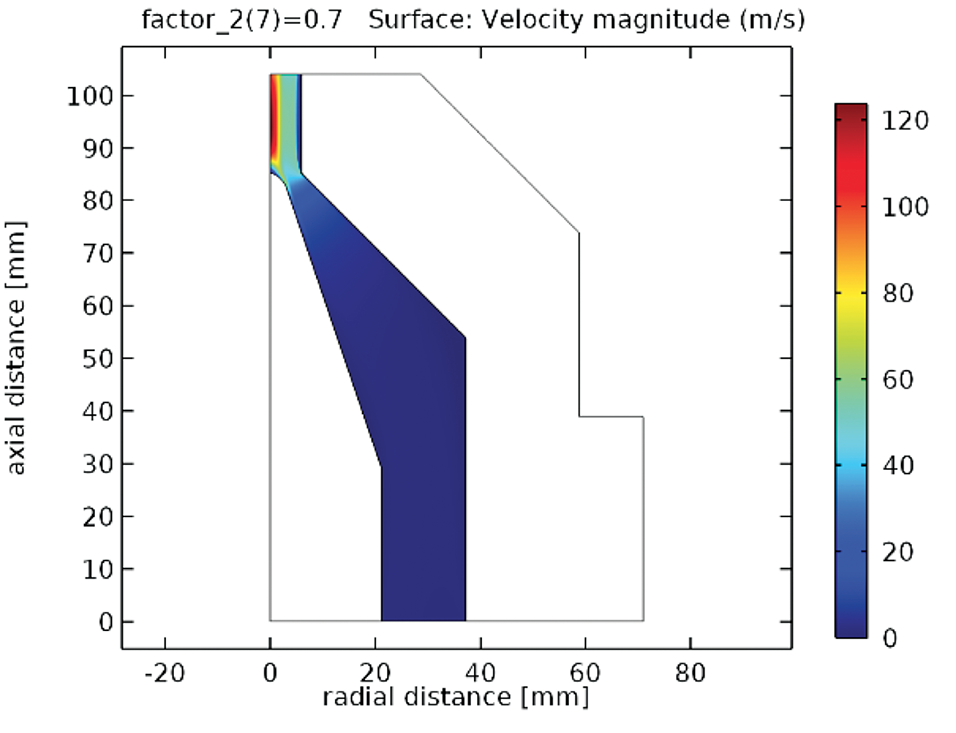
Figura 6. Campo de velocidad de la antorcha 2 (G = 6.35 STP m3/h, k1 = 0.291x10(-1) m2/s, Jn= 0.7x107 A/m2).

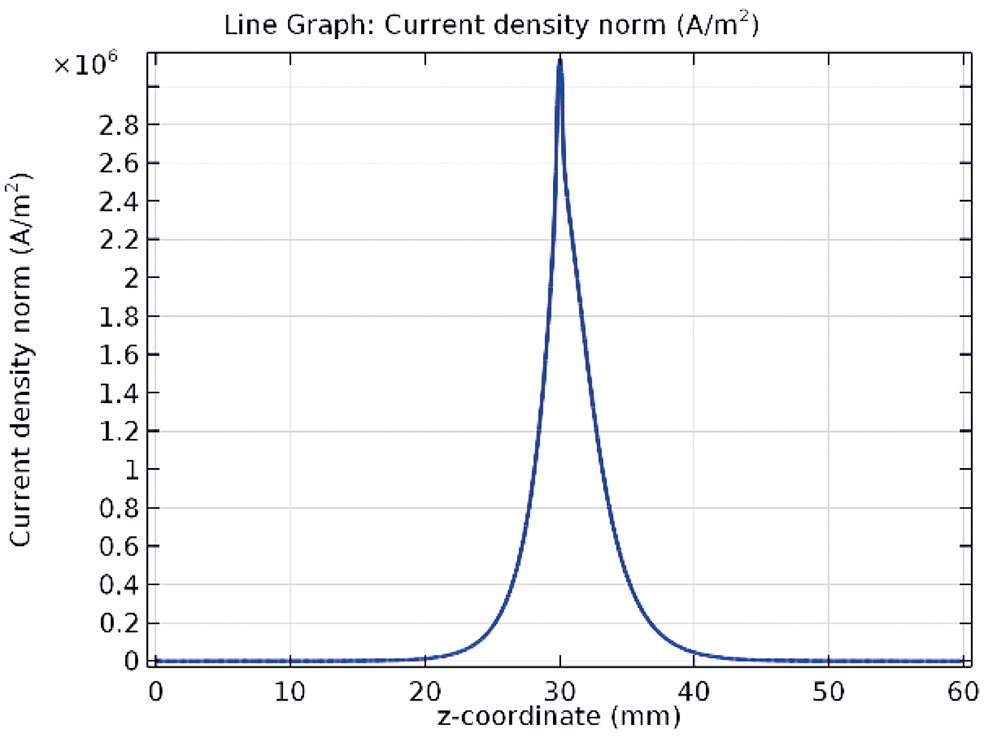
Figura 7. Densidad de corriente normal en la pared interior del ánodo de la antorcha 1 (G= 2.0 STP m3/h, k1 = 4.86x10(-3) m2/s, Jn= 0.8x108 A/m2).

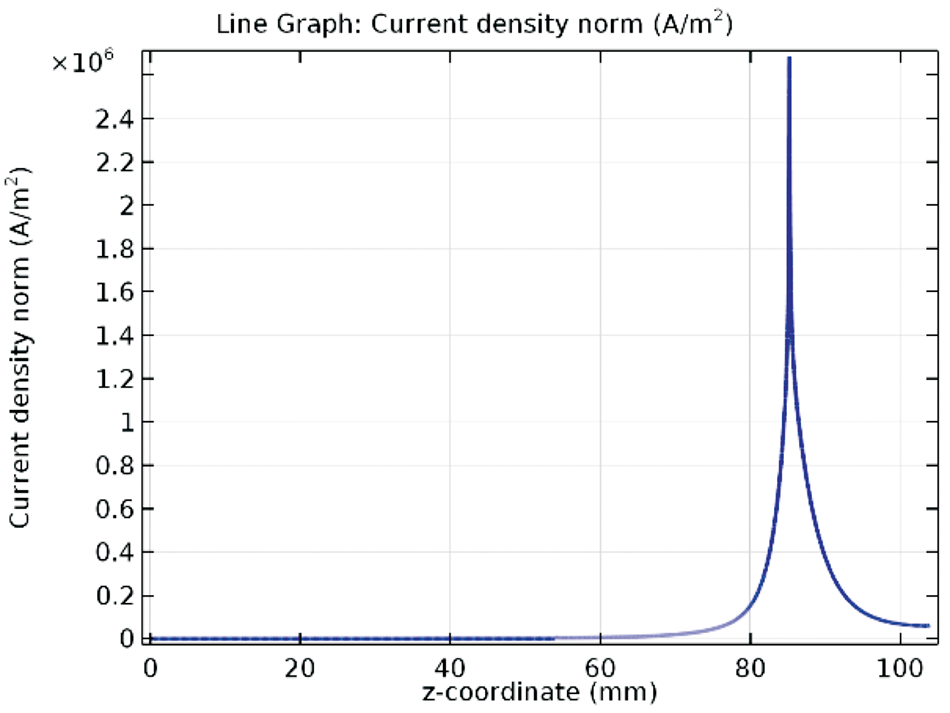
Figura 8. Densidad de corriente normal en la pared interior del ánodo de la antorcha 2 (G = 6.35 STP m3/h, k1 = 0.291x10(-1) m2/s, Jn= 0.7x107 A/m2).

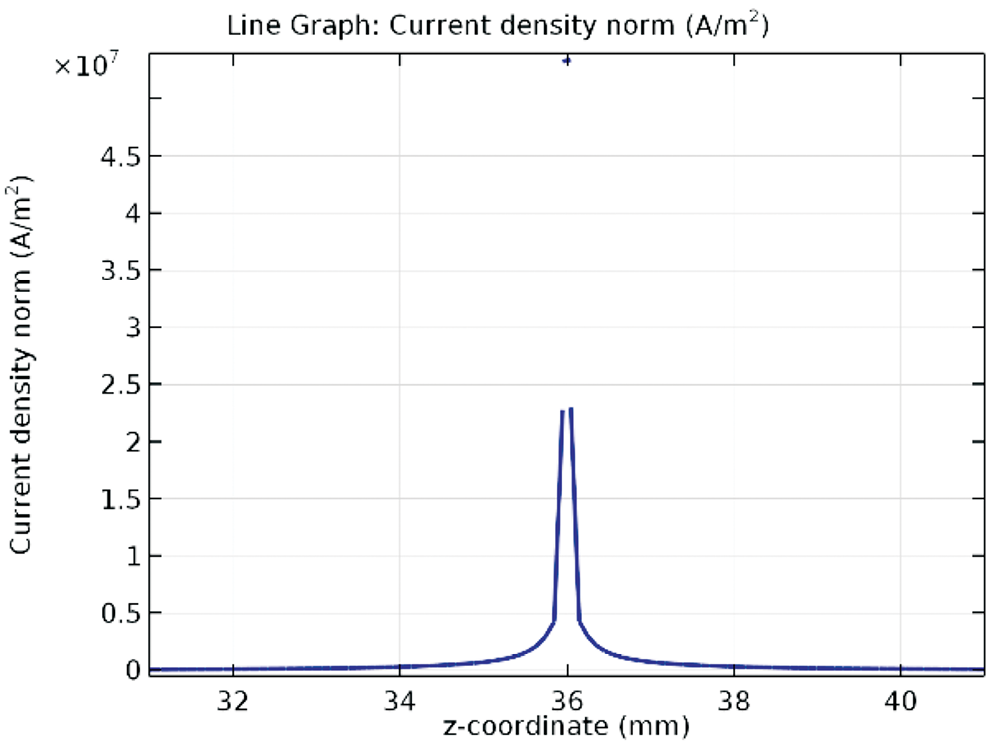
Figura 9. Densidad de corriente normal en la pared interior del ánodo de la antorcha 1, variando la posición de la base del arco (G = 2.0 STP m3/h, k1 = 4.86x10(-3) m2/s, Jn= 0.4x108 A/m2).

Los nuevos campos de temperatura y velocidad de la antorcha 1 se presentan respectivamente en las figuras 10 y 11. Se observa que, hasta usando un valor más pequeño de densidad de corriente en la punta del cátodo, se obtiene la misma magnitud de temperatura máxima del caso anterior de la figura 3 y sobre todo un valor doble de velocidad comparando con la figura 4.

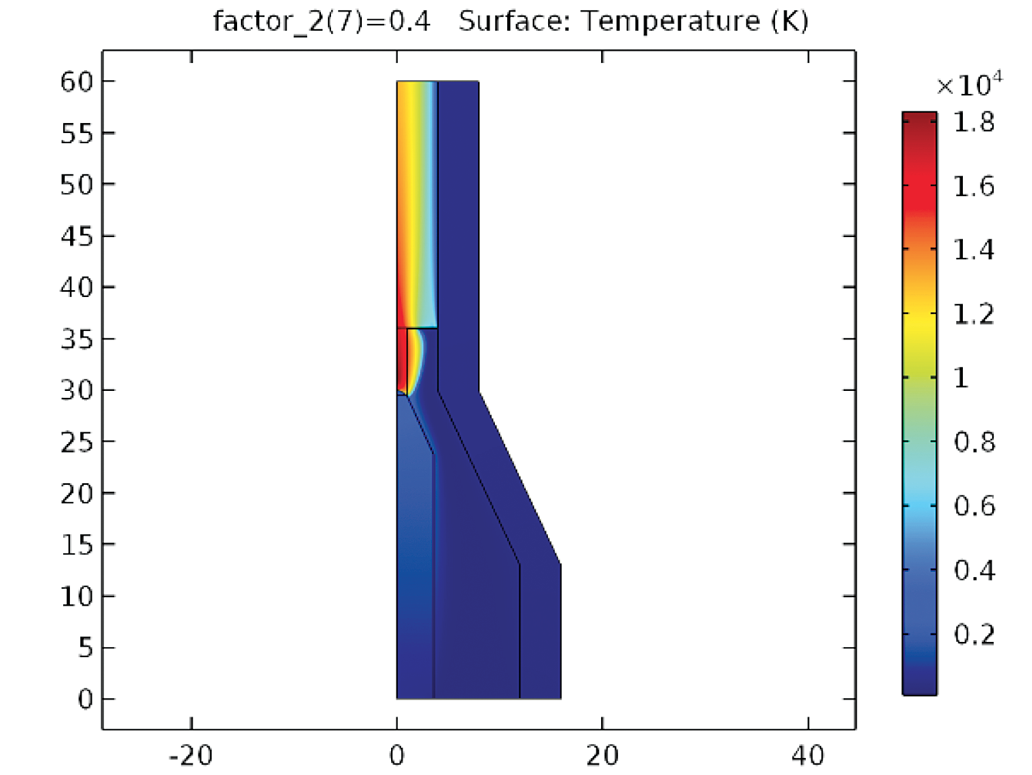
Figura 10. Campo de temperatura de la antorcha 1, variando la posición de la base del arco (G = 2.0 STP m3/h, k1 = 4.86x10(-3) m2/s, Jn= 0.4x108 A/m2).

Conclusiones

Se ha desarrollado un modelo computacional de una antorcha de plasma DC de arco térmico no transferido y han sido simuladas dos tipologías de antorchas, en particular:

• el modelo es estacionario, axis-simétrico, bi-dimensional e incorpora el flujo laminar débilmente compresible del plasma, los mecanismos de transporte de la energía térmica y los campos electromagnéticos presentes en la antorcha;

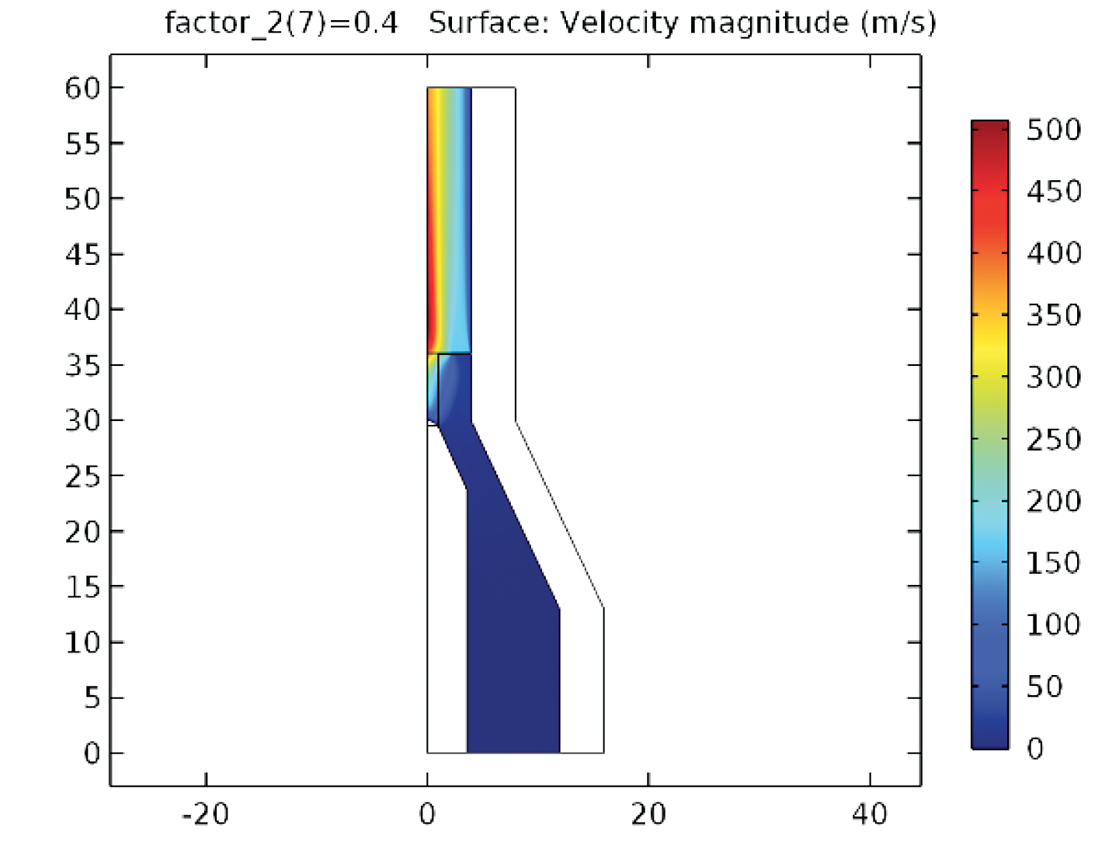
Figura 11. Campo de velocidad de la antorcha 1, variando la posición de la base del arco (G = 2.0 STP m3/h, k1 = 4.86x10(-3) m2/s, 0.4x108 A/m2).

• para resolver las ecuaciones diferenciales de las corrientes eléctricas y del campo magnético en la región del plasma y en el ánodo, se han adoptado condiciones de frontera específicas y se ha seleccionado la estrategia numérica de resolución;

• han sido modeladas y calculadas las fuerzas de Lorentz y los efectos del calentamiento Joule, que acoplan distintos fenómenos físicos de la antorcha;

• para evaluar el efecto de la posición de la base del arco en la pared del ánodo, han sido simulados nuevos casos y determinados los nuevos campos de velocidad y térmicos, variando justamente la posición de la base;

• los resultados numéricos de la temperatura del plasma, su velocidad y de la posición de la base del arco son bastante satisfactorios y se comparan con los de otros autores.

Agradecimientos

Se agradece la Vicerrectoría de Investigación y Extensión por la colaboración brindada en el marco del proyecto I- PLARE TORCH: Diseño y simulación de una antorcha de plasma térmico de arco no transferido para el tratamiento de residuos, código 5401-1490-2001.

Referencias

[1] M. I . Boulos, P. Fauchais and E. Pfender, Thermal Plasmas: Fundamentals and Applications, Plenum Press, New York, 1994.

[2] P. Colombo, G. Brustain, E. Bernardo and G. Scarinci, “Inertization and reuse of waste materials by vitrification and fabrication of glass-based products”, Curr. Opin. Solid State Mater. Sci. , 7, 225–239, 2003.

[3] Y. M. Kuo, T. C. Lin and P. J. Tsai, “Immobilization and encapsulation during vitrification of incineration ashes in a coke bed furnace”, Journal of Hazardous Materials, 133, 75–78, 2006.

[4] A. Gleizes, J.J. Gonzalez and P. Freton, “Thermal plasma modelling”, Journal of Physics D: Applied Physics, 38, R153–R183, 2005.

[5] J. Herbelein and A. B. Murphy, “Thermal plasma waste treatment”, Journal of Physics D: Applied Physics, 41, 2008.

[6] E. Gomez, D. Amutha Rani, C.R. Cheeseman, D. Deegan, M. Wise and A.R. Boccaccini, “Thermal plasma technology for the treatment of wastes: A critical review”, Journal of Hazardous Materials, 161, 614-626, 2008.

[7] S. Y. Mashayak, “CFD modeling of plasma thermal reactor for waste treatment,” MSc. Thesis, Mechanical Engineering. Purdue University, West Lafayette, Indiana, 2009.

[8] J.P. Trelles, C. Chazelas, A. Vardelle, and J.V.R. Heberlein, “Arc plasm torch modeling”, Journal of Thermal Spray Technology, 18, No. 5/6, 728-752, 2009.

[9] He-Ping Li, E. Pfender and Xi Chen, “Application of Steenbeck’s minimum principle for three dimensional modelling of DC arc plasma torches”, Journal of Physics D: Applied Physics, 36, 1084-1096, 2003.

[10] B. Selvan, K. Ramachandran, K.P. Sreekumar, T.K. Thiyagarajan and P.V. Ananthapadmanabhan, “Numerical and experimental studies on DC plasma spray torch”, Vacuum, 84, 442-452, 2010.

[11] Deng Jing, Li Yahojian, Xu Yongxiang and Sheng Hongzhi, “Numerical simulation of fluid flow and heat transfer in a DC non-transferred arc plasm torch operating under laminar and turbulent conditions”, Plasma Science and Technology, 13, vol. 2, 201-207, 2011.

[12] N.Y. Mendoza Gonzalez, L. Rao, P. Carabin, A. Kaldas and J.L. Meunier, “A three-dimensional model of a DC thermal plasma torch for waste treatment applications”, International Symposium on Plasma Chemistry ISPC-19, July 27-31, Bochum, Germany, 2009.

[13] He-Ping Li and Xi Chen, “Three-dimensional modelling of a dc non-transferred arc plasma torch”, Journal of Physics D: Applied Physics, 34, L99-L102, 2001.

[14] J.A. Mozingo, “Evaluation of a strut-plasma torch combination as a supersoni igniter-flameholder”, MSc. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, Virginia, USA, 2004.

[15] B. Chiné, M. Mata, I. Vargas, “Modeling a DC plasma with Comsol Multiphysics”, Comsol Conference 2015, October 14-16, Grenoble, France, 2015.

[16] Comsol AB, Comsol Multiphysics-CFD Module, User’s Guide, Version 5.1, 2015.

[17] Comsol AB, Comsol Multiphysics-Heat Transfer Module, User’s Guide, Version 5.1, 2015.

[18] Comsol AB, Comsol Multiphysics-AC/DC Module, User’s Guide, Version 5.1, 2015.

[19] Comsol AB, Comsol Multiphysics-Plasma Module, User’s Guide, Version 5.1, 2015.

[20] B. Chiné, “A 2D model of a DC plasma torch”, Comsol Conference 2016, October 12-14, Munich, Germany, 2016.

[21] A. H. Dilawari, J. Szekely and R. Westhoff, “An assessment of the heat and fluid flow phenomena inside plasma torches in non-transferred arc systems”, ISIJ International, 30, 381-389, 1990.

[22] C.L. Felipini and M.M. Pimenta, “Some numerical simulation results of swirling flow in d.c. plasma torch”, 15th Latin American Workshop on Plasma Physics, Journal of Physics: Conferences Series, 591, 01238, 2015.

---