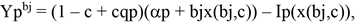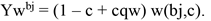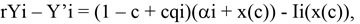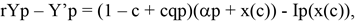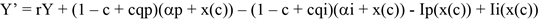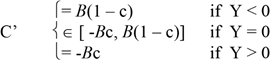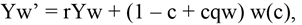Article
DOI:
https://doi.org/10.18845/te.v16i3.6356
Allocation of entrepreneurial and innovative talent: An economic model based on institutionally-driven relative rewards
Asignación del talento emprendedor e innovador: Un modelo económico basado en recompensas relativas impulsadas institucionalmente
TEC Empresarial, Vol. 16, n°. 3, (September - December, 2022), Pag. 1 - 15, ISSN: 1659-3359
AUTHORS
Yancy Vaillant

Department of Strategy, Entrepreneurship & Innovation, TBS Education 1 Place Alphonse Jourdain, 31068 Toulouse Cedex 7, France.
y.vaillant@tbs-education.fr.
![]()
ABSTRACT
Abstract
To master the force of innovation that sparks economic prosperity and growth along the lines of Schumpeterian creative destruction, it is important to understand what guides the entrepreneurial and innovative talent needed to fuel this spark. This paper presents an economic model that mathematically develops and visually represents the entrepreneurial career decisions of individuals and the allocation of entrepreneurial talent across an economy. The model is based on an institutional theoretical framework, where the external formal or informal constraints (institutions) of local society guide the choices of individuals towards innovative entrepreneurial careers. This model closely derives from prior relative reward models developed by Acemoglu (1995) to explain how the local relative rewards structure governs the entrepreneurial career decisions of individuals, and these decisions determine the allocation of entrepreneurial and innovative talent in an economy.
Keywords: Relative rewards, Institutional frameworks, Entrepreneurial career, Innovativeness, Talent allocation.
Resumen
Para dominar la fuerza de la innovación que desencadena la prosperidad económica en la línea de la destrucción creativa de Schumpeter, es importante comprender qué guía al talento empresarial e innovador necesario para alimentar esta chispa. Este artículo presenta un modelo económico que desarrolla matemáticamente y representa visualmente las decisiones de carrera empresarial de los individuos y la distribución del talento empresarial en una economía. Basado en la teoría institucional, el modelo presenta las restricciones institucionales formales o informales externas de la sociedad local que guían la elección de los individuos hacia carreras empresariales innovadoras. El modelo se deriva estrechamente de los modelos de recompensas relativas desarrollados por Acemoglu (1995) con el objetivo de explicar cómo la estructura de recompensas relativas local gobierna las decisiones de carrera empresarial de los individuos, así como explicar cómo estas decisiones determinan la asignación de talento empresarial e innovador en la economía.
Palabras clave: Recompensas relativas, Marco institucional, Carrera emprendedora, Innovación, Asignación de talento.
Introduction
1. Introduction
The creative destruction principals proposed by Schumpeter (1939) relied on the supply of entrepreneurial talent within an economy that was able to innovate, bring new value to the economy and therefore prompting it out of an equilibrious status quo and spurring new economic development. Despite the essential role of innovators within this highly influential view of economic development, much debate has existed ever since on where such innovation should best originate (Dosi, 1988; Cantwell, J., & Fai, 1999). For most of the twentieth century corporate-led innovation was seen as the greatest contributor of innovative value added (Burgelman & Sayles, 1988; Granstrand & Sjölander, 1990). But the 21st century has focused much more on the role of entrepreneurial start-up-based innovation as a significant contributor of innovation to the economy (Acs & Audretsch, 2005; Baumol & Strom, 2007; Carree & Thurik, 2010). As a result, many policy initiatives and academic programs have been developed to guide individuals towards adopting a self-employed entrepreneurial career as an alternative to labor market participation (Pihie & Akmaliah, 2009; Lanero et al., 2016).
However, not all entrepreneurial initiatives are necessarily ‘innovative’ in nature (Drucker, 2014). Only a fraction of entrepreneurial activity really serves towards economic development from a creative destruction perspective (Dosi et al., 2006; Spencer et al., 2008). As such, innovative talent must not simply be guided between labor market versus entrepreneurship career choices as a means of attaining optimal economic bearing, but they must also be encouraged towards an entrepreneurial career path that is innovative in nature if the goal is to incite the theorized economic growth benefits of creative destruction (Hagedoorn, 1996; Asante & Affum-Osei, 2019).
The presence of a favorable institutional framework with entrepreneurial role models, social inclusion policy and targeted entrepreneurship promotion measures can do a lot to change institutional structures and encourage potential talent to adopt entrepreneurial careers (Lafuente et al., 2007). People can be better incentivized towards decisions to exploit innovative entrepreneurial opportunities (Bayon et al., 2015). This can lead individuals from entrepreneurially alienated segments of the population (e.g., women, youths, immigrants) to choose an innovative entrepreneurial career path that will optimize their human capital and better serve the economy (Driga et al., 2009; Lafuente & Vaillant, 2013). To the contrary, in an economy where formal and informal constraints generate disincentives for innovative entrepreneurial behavior, it can be expected that the economy will see less of such behavior. Bankruptcy laws, personal liability of entrepreneurial risk, and social stigma towards entrepreneurial failure are all institutional constraints that are likely to attenuate the propensity of individuals towards more risky innovative entrepreneurial decisions (Vaillant & Lafuente, 2007; Bayon et al, 2016).
In this paper, an economic model is mathematically developed and visually represented that would explain the entrepreneurial career decisions of individuals and the allocation of entrepreneurial talent across an economy. The model is based on an institutional theoretical framework, where the external formal or informal constraints (institutions) of local society guided the choice of individuals towards innovative entrepreneurial ventures. This model, based on the influence of relative rewards in an economy, was derived from prior models developed by Acemoglu (1995) to explain the rent-seeking behaviors of individuals. As such, the model proposed in this paper explains how the local relative rewards structure governs the entrepreneurial career decisions of individuals, and these decisions determine the allocation of entrepreneurial and innovative talent in an economy.
In the following section, we will present the theoretical underpinnings of the institutional economic theory at the foundation of our economic model’s mechanics. We will then gradually develop the model in Section 3, first beginning with a simple static model, followed by a dynamic extension, and finally by proposing the addition of a non-pecuniary influence to our model coming from informal institutional rewards. The paper closes within some concluding remarks that include implications for future research.
2. Theoretical underpinnings
2. Theoretical underpinnings
2.1 Institutional Economic Theory
In order to understand better the underlying thinking behind the relative rewards model developed in this paper it is useful to first present the Institutional Economic Theory upon which its principals are based (mostly developed by Douglas North, 1990; 1996; 2005).
Institutional economic theory develops a very wide concept of “institution”. North (1990: 3) proposes that “institutions are the rules of the game in a society”. Institutions, according to this author, include any form of constraint that human beings devise to shape human interaction. Institutions can be either formal - such as political rules, economic rules and contracts - or informal - such as codes of conduct, attitudes, values, norms of behaviour, and conventions, or rather the culture of a certain society. North (1990) attempts to explain how institutions and institutional framework affect economic and social development. The main function of institutions in a society is to reduce uncertainty by establishing a stable structure for human interaction.
According to North (1996), formal institutions are subordinate to informal ones in the sense that they are the deliberate means used to structure the interactions of a society in line with the norms and cultural guidelines that make up its informal institutions. Policy making that attempts to change the formal institutions of society will therefore have little success if it does not first adjust the informal institutions in a compatible way. The difficulty rises from the fact that, whereas a governing body can influence the evolution of a society’s formal institutions in a rather direct way, informal institutions are much less tangible and usually fall outside the direct influence of public policy. They can be moulded, but tend to resist change and take time to evolve towards new social norms.
Together with the theoretical amplitude that the institutional economic theory offers, the historical perspective and institutional embeddedness argument which it offers are especially ideal for the study of entrepreneurial activity from a territorial point of view. This therefore forms the theoretical backbone guiding mechanics of the relative rewards model guiding the distribution of entrepreneurial talent developed in this paper.
2.2 Informal Institutions
The institutional evolution argument included within the economic institutional theory is especially important for the study of entrepreneurial activity since some of the main distinctions that separate territories across economies and territorial boundaries lies in the institutional history and entrepreneurial tradition, specific to every region. North (1981; 1990) explains using an institutional approach how there can exist ‘radically differential’ performance of economies over long periods of time. According to North (1990), the interactions between institutions and organisations (economic, political, or social) shape the direction of institutional change. Institutions determine the opportunities of society and organisations are created to take advantage of these opportunities. As the organisations evolve, they alter the institutions. The resultant path of institutional change, according to this author, can, on the one hand, lead to a stagnant situation where institutions come to serve the sole purpose and interests of maintaining existing organisations, or on the other hand, can lead to a ‘lock-in’ that comes from the symbiotic relationship between institutions and evolving organisations as a consequence of the incentive structure provided by those institutions and the dynamic feedback process by which ‘human beings perceive and react to changes in the opportunity set’ (North 1990: 7).
North followed-up his path dependency argument by describing the embedded character of informal institutions as a result of their cultural content. Pilon and DeBresson (2003) reinforced a similar argument in their study of innovative districts identifying local cultural ‘anchoring’ based on cultural similarities, cultural cohesiveness, and historical particularism and heritage, making certain geographical areas more conducive to innovative entrepreneurial activity.
The same argument holds within the theoretical framework established within the institutional economic theory and the relative reward model described below, which serves to explain the allocation of entrepreneurial and innovative abilities across economies.
3. Relative Rewards, and Model Development
3. Relative Rewards, and Model Development
Relative Rewards are derived from the different valuations that individuals attach to different entrepreneurial career choices. These valuations are based not only on pecuniary rewards but also include non-pecuniary rewards based on social, psychological and emotional factors. Every individual perceives the rewards (and costs) associated with different entrepreneurial career decisions differently depending on, internal factors particular to every individual, and on external factors and constraints, formal and informal, which affect every individual somewhat distinctively depending on their particular characteristics. The way in which an individual perceives the rewards associated to a particular entrepreneurial career decision relative to other alternative decisions will largely influence and guide the choices of that particular individual. An individual will usually take the entrepreneurial career decisions that s/he perceives will contribute to the highest pecuniary and non-pecuniary rewards relative to all other available alternative decisions.
The rewards of all available entrepreneurial career decisions of an individual relative to all others at any moment in time constitute the relative reward structure of the individual at this specific point in time. Because the perceived rewards associated to any decision are largely determined by internal and external factors that are dynamic in nature, the relative reward structures of individuals will change over time. Because every individual is distinct, because the decisions available to every individual vary, and because the internal and external factors influencing every individual’s decisions are particular, every individual in an economy has her/his own specific relative reward structure.
Although every individual has her/his own particular relative reward structure, at any particular point in time, it is often possible to cluster individuals of an economy with relatively similar relative reward structures into distinctive socio-economic groups. Aggregated to the economy as a whole, the resulting relative reward structure will largely determine the present and future entrepreneurial, economic and technological development of the economy.
3.1 - A Simple Model 1
We assume that each agent has some talent that can be employed in two areas:
1. Innovative entrepreneurial activities which we call innovation (i),
2. Non-innovative entrepreneurial activities which we call proprietorship (p).
We will later add a third activity which will permit our subjects to choose to work for others (w). We include the imitator and the rent-seeker2 under the proprietor category since, as the proprietor, both these groups do not contribute significantly to technological growth. The important aspect for us is that agents can choose the activity that maximises the returned ‘value’ on investment.
For now, we assume that the economy consists of a continuum of identical agents normalised to 1 (we will relax this assumption later). Each agent undertakes an ex-ante investment that will determine his/her total product. In the absence of constraints, this total product is equal to α k+x, where k ∈ [i, p] (innovator or proprietor) and where x is the amount of investment undertaken by the agent in question. This investment has to be chosen from the set [0.∞) and has cost Ik(x) with Ik’(·) and Ik’’(·) > 0, limx 0 Ik’(x) = 0 and Ik(0) = 0. However, in the presence of constraints, the agent does not realise all the revenues he can potentially produce. The agent may face constraints which can either be formal institutionalised constraints such as taxes or capital constraints or they can be more informal in nature such as the presence of uncertainty, lack of information or knowledge. Of-course there is an almost infinite number of constraints which we will not go into at this point. 3 Hence in the presence of constraints, the agent will lose a proportion (1 - qk) of his/her potential product. We assume that, qi ≤ qp, and consequently that (1 - qi) ≥ (1 - qp). This usually holds in reality since innovation decisions are relatively more sensitive to constraints. 4 We illustrate the level of constraint as a proportion c. Therefore, the total net return to the agent is equal to
(1)
The potential revenue of the agent is (αk + x) and the agent gets all of this only to the proportion (1 - c) and only a proportion qk of it with probability c, while the cost of investment is always incurred. 5 The investment level will be set to maximise this return which implies
(2)
where δk(·) is the inverse function of Ik’(·), and Ik’’(·) > 0 implies that x(c) is everywhere decreasing in c. It can readily be seen from Eq. (2) that when c is positive, entrepreneurs will under-invest since they will not collect the full return that they potentially could generate.
The expected return to entrepreneurship can be formulated as
(3)
The first order condition for optimal investment can be seen as
(4)
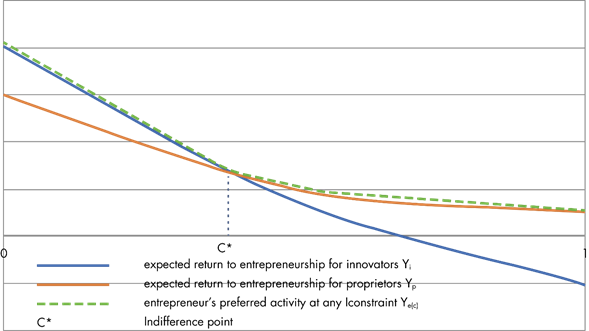
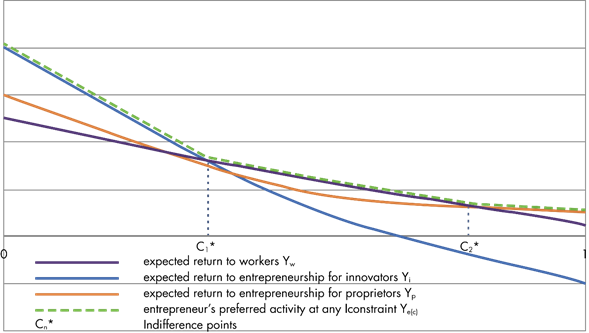
Thus, both curves, for the innovator and the proprietor, are downward sloping and can have intersections (indifference points) depending on the relative positions of these curves.
Condition A. αi + x(0) - Ii(x(0)) > αp + x(0) - Ip(x(0)).
This states that when there are no constraints, the return to innovation is greater than simple proprietorship.
Condition B. Ǝc* such that (1 - c* +c*qi)(αi + x(c*)) - Ii(x(c*)) = (1 - c* +c*qp)(αp + x(c*)) - Ip(x(c*)).
This condition implies that at some level of constraint in the economy, simple proprietorship is equally profitable to innovation.
Proposition #1. Given that c* is not a tangency point of Yi and Yp, then at any level
ç < c* Yi, the entrepreneur will prefer to innovate,
ç = c* Intersection, the entrepreneur is indifferent towards innovation or proprietorship,
ç > c* Yp, the entrepreneur will prefer to be a simple proprietor.
Running a lagrangian function which maximises Yk, where k ∈ [ i, p], such that proposition one holds, we get a function Ye(c), which gives the entrepreneur’s preferred choice of activity at any level of constraint. This is illustrated as the bold dashed line in Figure 1.
Figure 1: Entrepreneur's Preferred Activity According to Level of Constraint
We will now add the third alternative opened to our agents, that of becoming a worker. We can write the expected returns to the worker as
(5)
where,
(6)
and although it does not affect our analysis we can intuitively deduce that
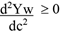
Condition C. Ye(x(0)) > w(0).
This states that when there are no constraints, the return to entrepreneurial activities are greater than the return to the worker 6 .
Condition D. Ǝc* such that Ye = (1 - c + cqw) w(c)
This condition implies that at some levels of constraint in the economy, being a worker offers a return equal to that of entrepreneurial activity. More than one such points are possible.
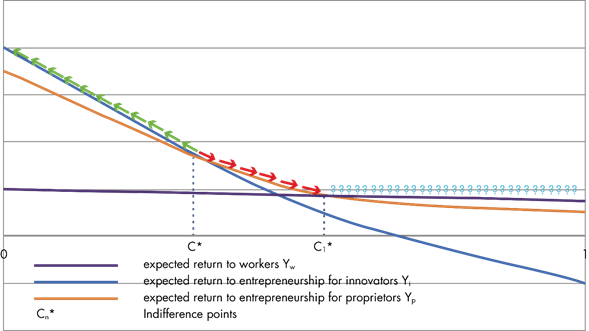
Proposition #2. Given that c* is not a tangency point of Ye and Yw, and j ∈ [ 1, 2] such that c*1 < c*2 where c*2 may or may not exist, then at any level
ç < c*1 Ye, the agent will prefer to be an entrepreneur,
ç = c*j Intersection, the agent is indifferent towards being an entrepreneur or a worker,
c*1 < ç < c*2 Yw, the agent will prefer to be a worker,
ç > c*2 Ye, the agent will prefer to be an entrepreneur.
Running a lagrangean function which maximises Yk, where k ∈ [ e, w], such that proposition two holds, we get a function Y*(c), which gives the agent’s preferred choice of activity at any level of constraint. This is illustrated as the dashed bold line in Figure 2.
Figure 2: Agent's Preferred Activity, work or venture, According to Level of Constraint
We must now relax our assumption of agent uniformity to allow for heterogeneity of innovative/entrepreneurial talents. To do this, we must adapt the returns on investments to bjx where bj is the type of the agent which has a distribution over [ 0, 1] given by G(b), so that Eqs. (4) & (5) can be transformed to
(8)
(9)
We could now rebuild our model using these adapted return-on-investment equations which allocate for heterogeneity in innovative/entrepreneurial talent and evaluate according to the marginal agent being indifferent between activity choices.
We can think of investments into innovative activities as creating positive externalities affecting the investment decision of other entrepreneurs7 (generating new technological opportunities, aggregate demand, reduced uncertainty, reduced constraints from the beaten path, or labour market externalities). On the other hand, investments into non-innovative proprietorships have mostly negative externalities affecting technological growth not just due to the resources which they orient away from innovative activities, but also for promoting a slowdown in rates of obsolescence which disfavour innovative behaviour (Gifford, 1992: 269)8.
Propositions #1 & #2 establishes that the allocation of talent is determined by the relative rewards created out of the institutional constraints of an economy, which permit the reward structure to vary considerably across amplitudes of constraints to innovation. Similar to Baumol’s (1996) argument, ‘that even though the supply of entrepreneurial talent is not sensitive to relative rewards, the allocation of this talent is’9. We are clearly demonstrating this with our model: the supply of talent is fixed but its distribution across activities crucially depends upon the relative rewards, which however, are also determined endogenously in our model.
3.2 - Dynamic Extension to the Model
Let us now consider a continuous time analogue of our model with overlapping periods. Leaving the worker out for the moment, each entrepreneur can potentially be infinitely active but faces an exit rate of B per period and also there are B new entrepreneurs who enter/initiate their investment at every instant, implying a constant population. Each entrepreneur has to make an irreversible investment choice at the start of each period, but can modify their choice from period to period. This is not too unrealistic since it can be imagined that an entrepreneur making an investment decision will be somewhat tied to this investment for a certain period before he can pull his resources out of this investment and reorient them towards a new activity. The per period returns are the same as given earlier with a discount rate adjusted for the probability of exit, denoted by r. This description implies that each entrepreneur, when initiating a new period, observes the level of constraints c, and anticipating the choice of future entrants due to the externalities which they bring, makes her own choice. Also, each entrepreneur chooses her investment level at each instant and this only influences her total product at that point. The investment level will therefore only depend on the current level of constraint in the economy, which we again write as x(c). The following value equations can therefore be written (dropping time arguments);
(10)
(11)
where the prime denotes a time-derivative. As return to innovation is given by Yi and that to proprietorship by Yp, innovation will be more attractive than proprietorship when Yi > Yp and new entrants would prefer entrepreneurship to proprietorship. Alternatively, we can define Y = Yi - Yp, and innovativeness will be more attractive than proprietorship when Y > 0. Subtracting (10) from (11), we obtain the law of motion of Y as
(12)
Let c*(t) be such that, Y(c*(t)) = 0. When c*(t) < c(t), entrepreneurs entering a new period would like to be innovators. However, as the investment choice is irreversible, c(t) is a predetermined variable and cannot jump to c*(t). Thus, when Y > 0, all entrepreneurs entering a new period would choose to invest in innovation and c would only fall due to the exit of existing proprietors. This change in c would take place at the rate Bc. Similarly when Y < 0, all entrepreneurs entering a new period would become proprietors but the increase in c will be equal to B(1 - c). These entrepreneurs would only have to choose when they would be indifferent between new investments alternatives, when Y = 0. Thus, the law of motion of c will be given by the following equation;
(14)
C’ is then the representation of historical dependence in our model. Therefore, depending on where the economy starts, the long-run behaviour can be very different. In particular an economy which inherits an unfavourable allocation of entrepreneurial talent away from innovative activities, will have higher relative rewards for proprietorship activities and even-tually converges to a ‘steady-state’ with high proprietorship at the expense of innovativeness. Where an economy inherits higher relative rewards to innovation, momentum in the level of innovativeness will build with every new generation of investment and an innovative ‘steady-state’ will be established.
As observed by Acemoglu (1995: 27) for his similar model, the economic interest of the dynamic extension to our model is in the emphasis it places upon how fast allocations of talent influence future reward structures (Figure 3). If the majority of the investors in the current period choose to become proprietors, the return to innovation relative to that of proprietorship will be reduced in future periods and future generations of investors will be induced to choose proprietorship, thus giving us history dependence. Initial differences can have important long-run effects. Also, reversing the adverse effects on technological growth of a misallocation is difficult because such a misallocation also leads to an unfavourable future reward structure.
If we reincorporate the option for our agents to join the labour force, where
(15)
then Bc, when the relative rewards influence the allocation of talent towards the labour force, remains unknown and unpredictable. Also, beyond the scope of our model is determining the influence of the labour market on technological growth and innovativeness.
Figure 3: Dynamic Choice of Preferred Activity According to Constraints
3.3 - Non-pecuniary rewards, social consensus, and historical dependence 10
So far, our model has only dealt with the pecuniary (the money) aspects of the relative reward structure. But as we have mentioned in the sections of this paper that preceded our model, non-pecuniary rewards are also very important in the allocation of entrepreneurial talents within an economy. A great deal of non-pecuniary rewards is exogenously determined, and can only be captured by our model as adjustments up (positive rewards) and down (for negative rewards) of the different Yk curves. This would influence the relative rewards within our model in a static way, but would not collaborate our dynamic interpretation of it. But Acemoglu (1995: 29) identified a series of non-pecuniary rewards which did influence the allocation of talent in a dynamic and endogenous manner. The inclusion of these endogenously determined non-pecuniary rewards then strengthens the history dependence emphasised earlier.
Societies with high innovation levels will be less willing to constrain the entrepreneurs who innovate; therefore, innovation is more likely to persist. But this argument fits less well in the case where high levels of proprietorship exists. A proprietor will be relatively less eager to have new entrants investing in innovation, especially if the existing proprietors could choose a scheme which would not hurt themselves but make innovation (and entrepreneurship altogether) less attractive for new entrants. But it is generally difficult to ‘create’ a discriminating reward structure. Therefore, where there is a higher amount of proprietorship (it could also be argued that where there is a greater concentration of influence with proprietors), there may also be a weaker political will to improve the allocation of talent towards innovation.
But non-pecuniary aspects of the reward structure are not under the direct control of the government or any other group (North, 1990). A society’s attitude norms and value judgement can be much more powerful than political influence in determining the relative rewards of an economy. A society with high innovativeness will give relatively more respect to innovating entrepreneurs than a more stagnant society of proprietors (North, 2005). There are many channels by which the social attitudes are influenced. Learning by new generations will start from the already established norms and role models (Lafuente & Vaillant, 2013). This learning process will influence the views of the new generation as well as their stock of knowledge (Coleman, 1994, as reported in Acemoglu, 1995:30 ). This could mean that a social attitude such as social status may be determined both by external forces and through endogenous influence. Therefore, a social attitude such as the social status of a profession may depend on the choices that the rest of the society makes, and thus proprietorship may have less negative stigma when it is more ‘wide-spread’ (Vaillant and Lafuente, 2007). Finally, a society’s value judgement may conform to past practice or economic behaviour if individuals look for justification for their present place in society. Thus, entrepreneurs with innovative talents, who have placed their (irreversible) investments into proprietorship due to the relative reward structure, will gradually change their value judgements and will eventually pay more respect to being a proprietor (Bayon et al., 2016). Therefore, there seems to exist a mechanism which makes the social consensus, and the non-pecuniary rewards, respond to the economic decisions of the agents.
An element of importance which we can extrapolate from this discussion is that the link between past allocation and non-pecuniary rewards implies that after a misallocation of talent, not only will pecuniary rewards favour non-innovative activities and investments, but the society may also lack the ‘social/political will’ to change the status quo (Driga et al., 2009).
Our preceding model and the analysis which we have pulled from it suggests some important insight into the state of technological development in less developed regions (Vendrell-Herrero et al., 2020). Many less competitive economies can be thought as being caught in a low reward, low innovation, low technological growth trap from which escape is not easy. The fact that domestic technological stagnation and dependence on borrowed technologies has become a part of the cultures of these societies coheres well with the above view (Findlay, 1978). Entrepreneurially driven domestic technological development can therefore be a valid answer to technological growth in these societies (Yoruk & Jones, 2020).
Concluding
4. Concluding Remarks
This paper presented an economic model that explains the entrepreneurial career decisions of individuals and the allocation of entrepreneurial talent across an economy. The model is based on an institutional theoretical framework, where the external formal or informal constraints (institutions) of local society guided the choice of individuals towards innovative entrepreneurial ventures. This model closely derives from prior relative reward models developed by Acemoglu (1995) to explain the rent-seeking behaviors of individuals. As such, the model proposed in this paper mathematically explained and visually represented how the local relative rewards structure governs the entrepreneurial career decisions of individuals, and these decisions determine the allocation of entrepreneurial and innovative talent in an economy.
As with all economic models, the one developed and presented in this paper is a metaphorical representation of reality and is purely conceptual in nature. It is meant to form the basis upon which theory can be proposed and empirical verification carried out. Further research can build upon the proposed economic model to formulate propositions that can be empirically analysed and contrasted. The generalised character of the economic model can then be specified to fit the particularities of different geographical, industrial, or social contexts. To master the force of innovation and its economic role as the spark for economic prosperity and growth along the lines of Schumpeterian creative destruction, it is important to understand what guides the entrepreneurial and innovative talent needed to fuel this economic force.
Because entrepreneurial innovation and start-up-based value additions to the economy is increasingly being prioritized by many public administrations as a way to induce the digital and decarbonised transformation of local economies (Nambisan et al., 2019), understanding better how entrepreneurial and innovative talent is allocated across an economy is essential. Relative rewards are keys forces for entrepreneurial ecosystems as they regulate the resource allocation that combine institutions and human agency (Isenberg, 2010; Acs et al., 2018). By better grasping the influence of the relative rewards structure over this allocation, and the role of formal as well as informal institutions in establishing such relative rewards structures, public administrations and social agents can possibly be a greater force in moulding the innovative entrepreneurial career decisions of individuals within their entrepreneurial ecosystem.
Notes
[1] The model, although of own construction, has been inspired from similar models developed to illustrate allocation of talent/entrepreneurship in Baumol (1996), Murphy et al. (1991), Banerjee & Newman (1993), Acemoglu (1995), and Bassanini (1997). The layout and presentation of the model will largely be based on that used in Acemoglu (1995).
[2] Acemoglu (1995: 19) mentions some cases where rent-seekers, in a broad sence, may sometimes be productive (innovative), but we will ignore these rare exceptions in what follows and only focus on the margin.
[3] For a more exhaustive enumeration of constraints facing entrepreneurs see Brunetti et al. (1997).
[4] See Dosi (1997). The exceptional case where innovation is used to avoid constraints may exist, but we have assumed equal levels of c for all agents.
[5] We are implicitly assuming that agents have no need for credit. This is to facilitate the math, but the inclusion of credit furthers the strategic effect. The higher the constraint, the higher is the probability of bankruptcy and the higher will the cost of capital be thus making entrepreneurship even less attractive.
[6] This is a heuristic condition which we are imposing on the model, and not an assumption of the model as such. Of-course there may be many examples where the benefits to the worker are superior than those to the entrepreneur. This will become exactly our point, and will be looked into further on.
[7] Together with the arguments laid forward by the supporters of the role theory, many supporters of an evolutionary approach to entrepreneurial growth would tend to support the idea that innovativeness, as with stagnation, in an economy tends to feed on itself, Bassanini (1997), Dosi et al. (1999) among others.
[9] Acemoglu (1995) arrived at the same conclusion with his model comparing productive and unproductive economic activity. This is mostly the reason why we chose to develop our model on the same lines as his.
[10] Once again, this section, along with its title, are heavily inspired by the structure utilized in Acemoglu (1995).
References

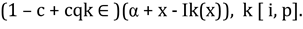
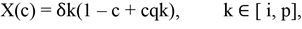
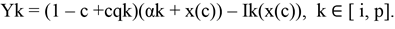
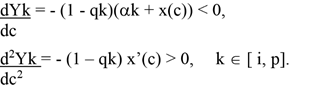
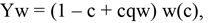
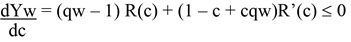
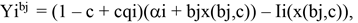 (7)
(7)