
Diferencias en la estimación del coeficiente de curtosis en diferentes softwares
estadísticos
Variations on kurtosis estimation with different statistics software
Luz Elena Barrantes Aguilar1
Fecha de recepción: 11 de febrero, 2019
Fecha de aprobación: 20 de junio, 2019
Vol.5 Nº 2 Julio- diciembre 2019
Barrantes Aguilar, L. (2019). Diferencias en la estimación del coeficiente de curtosis en diferentes softwares estadísticos. Revista E-Agronegocios, 5(2). https://doi.org/10.18845/rea.v5i2.4456
DOI: https://doi.org/10.18845/rea.v5i2.4456
1 Licenciada en Economía Agrícola y Agronegocios. Estudiante de la maestría en CIencias en Economía Agrícola y de los recursos naturales de la Universidad Autónoma Chapingo (UACh), México.
Correo electrónico: luz.barrantes@ucr.ac.cr
orcid id: https://orcid.org/0000-0001-5691-6657.

Resumen
La curtosis, o cuarto momento de una distribución, se emplea para describir una distribución y forma parte de algunos contrastes de normalidad. La mayoría de los paquetes estadísticos la incluyen, por lo que su cálculo es sencillo. Sin embargo, para un mismo grupo de datos, los resultados que proporcionan los diferentes programas estadísticos pueden diferir. Con el objetivo de explicar las diferencias en la estimación de la curtosis entre los paquetes estadísticos de mayor uso para los economistas agrícolas se emplearon dos muestras y se realizó una comparación en la estimación del coeficiente curtosis con nueve softwares estadísticos diferentes. Los resultados mostraron que las diferencias no se deben a errores de cálculo, sino a que el término se emplea de manera incorrecta por la mayoría de programas y se estimó que existe aproximadamente un 20% de probabilidad de llegar a una conclusión equivocada al trabajar con muestras pequeñas y no considerar el factor de ajuste.
Palabras clave: cuarto momento, exceso de curtosis, exceso de curtosis ajustado, software estadístico.
Abstract
Kurtosis, or a distribution’s fourth moment, is used to describe distributions and belongs to some normality contrast tests. Most of the statistical softwares include kurtosis, which makes the estimation to be relatively easy. Nevertheless, for a same data set, statistical softwares can provide a different result. The objective of this work is to depict kurtosis estimation differences between statistical softwares that are most commonly used among agricultural economists. Two samples were used to compare kurtosis coefficient estimation differences with nine different statistic softwares. Results shows that these differences are not due to a mistaken estimation procedure, but mainly because the term kurtosis is used wrongly. In conclusion, when working with a small sample size and adjustment factor is not considered, there is a 20% probability of making a mistaken conclusion.
Key words: fourth momentum, excess kurtosis, adjusted excess kurtosis, statistic software.
Introducción 2
El concepto de curtosis forma parte de la literatura desde hace más de cien años, cuando Pearson introdujo el concepto en 1905, por lo tanto, no se trata de un tema nuevo y a simple vista tampoco complejo; sin embargo, Finucan (1964) advirtió sobre el peligro de la simplificación hecha en algunos libros que reducían la curtosis a algo simplemente relacionado al pico de la distribución. Greene (2011 p.1058) define la curtosis como “una medida del grosor de las colas de la distribución”.
El tema de la curtosis ha sido ampliamente discutido, en los años 70 y 80 parte del debate giró en torno a qué mide este coeficiente, y cómo debe medirse. Los esfuerzos por desarrollar mediciones más robustas van desde medidas multivariantes (Mardia, 1970) o medidas basadas en cuantiles (Moors, 1988).
El coeficiente de curtosis está programado en la mayoría de los softwares estadísticos; forma parte de la estadística descriptiva que se puede obtener de una serie de datos. En su estimación, es común encontrar que los resultados varían según el software que se utilice; en algunos casos, independientemente de estas diferencias en los resultados, las conclusiones no varían; no obstante, puede suceder lo contrario y encontrarse en una situación donde se tiene resultados que llevan a diferentes conclusiones respecto a la forma de la distribución. Por tanto, estudiantes e investigadores(as) deben tener claridad de lo que verdaderamente se está calculando, de modo que se eviten errores de interpretación. El objetivo de este trabajo es explicar las diferencias en la estimación de la curtosis entre los paquetes estadísticos de mayor uso para los economistas agrícolas, mediante el uso de una muestra pequeña (n=25) y una muestra grande (n=166).
Referente teórico
La media, la varianza, la asimetría y la curtosis son los llamados momentos de una distribución. El tercer y cuarto momento, corresponden a las medidas de forma de una distribución que toman como referencia a la distribución normal. La curtosis mide el grado en que una distribución se aleja de la distribución normal, respecto al nivel de achatamiento o apuntamiento de su curva, estudiando la concentración de valores en la zona de la media, cuanto mayor sea la concentración en esta zona, mayor será su apuntamiento, por el contrario, si la concentración en la zona central es baja se dirá que la curva achatada (Fernández et al., 2002).
La distribución normal tiene una curtosis igual a tres, cuando esto sucede se dice que la distribu
2Este artículo se trabajó empleando puntos como separador de decimales, aunque las normas de autor de la revista estipulan que deben ser comas; esto debido al uso del software InfoStat para la construcción de histogramas, este no permite hacer cambios en el sistema decimal y por defecto emplea puntos para decimales, por lo que, con el fin de estandarizar, todo el escrito sigue este formato.
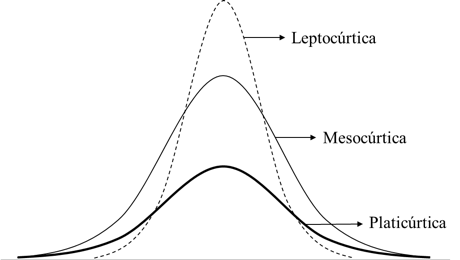
ción es mesocúrtica, puede ser que la distribución sea más achatada, esta se conoce como platicúrtica, y la curtosis toma valores menores a tres. El caso contrario se presenta cuando los datos están muy concentrados alrededor de la media, lo que genera una forma de la distribución más empinada, en este caso se trata de una distribución leptocúrtica y la curtosis toma valores mayores a tres (Figura 1).

Figura 1. Ejemplo de una distribución mesocúrtica (k=3), una leptocúrtica (k>3) y una platicúrtica (k<3)
.
La curtosis es independiente de la variabilidad, no necesariamente una distribución leptocúrtica tiene menos varianza y por eso es más apuntada; y tampoco la distribución platicúrtica por ser más achatada debe ser más variable. Una distribución leptocúrtica es muy apuntada en el centro, más que la normal, decae muy rápidamente en un primer momento, pero en los extremos es algo más alta que la distribución normal. Esto quiere decir que una distribución leptocúrtica es más probable que ofrezca más valores extremos que la distribución normal. El concepto de curtosis fue introducido en el contexto estadístico por Pearson (1905) basado en el griego kurtos (curvado o arqueado), y la define como:
(1)
Este encuentra que para la distribución normal y denomina a
para la distribución normal y denomina a 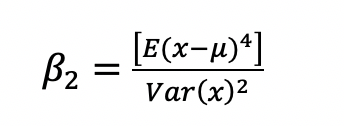 como grado de curtosis, que posteriormente es llamado exceso de curtosis. Y cuando la distribución es normal, el valor del error muestral lo define como:
como grado de curtosis, que posteriormente es llamado exceso de curtosis. Y cuando la distribución es normal, el valor del error muestral lo define como:
(2)
Si 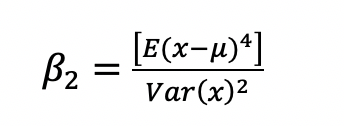 de una distribución de frecuencia difiere de cero en más de tres veces su error muestral no se puede considerar que la distribución sea mesocúrtica, por lo tanto, debe emplearse otra distribución diferente de la normal para representar la distribución (Seier, 2003). Para los años veinte el concepto ya aparecía en los libros de texto de estadística, en 1927 Student publicó un artículo sobre errores de análisis rutinarios, y en este incluyó una regla nemotécnica para recordar mediante dibujos, los conceptos de una distribución platicúrtica y una leptocúrtica (Figura 2).
de una distribución de frecuencia difiere de cero en más de tres veces su error muestral no se puede considerar que la distribución sea mesocúrtica, por lo tanto, debe emplearse otra distribución diferente de la normal para representar la distribución (Seier, 2003). Para los años veinte el concepto ya aparecía en los libros de texto de estadística, en 1927 Student publicó un artículo sobre errores de análisis rutinarios, y en este incluyó una regla nemotécnica para recordar mediante dibujos, los conceptos de una distribución platicúrtica y una leptocúrtica (Figura 2).

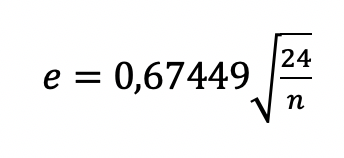

Figura 2. Regla nemotécnica para recordar la diferencia entre platicúrtico y leptocúrtico.
Fuente: Student (1927).
En la bibliografía, la fórmula para obtener el valor de este coeficiente de curtosis no se encuentra estandarizada, o eso es lo que parece. Existen otros conceptos como el exceso de curtosis, la L-kurtosis, el coeficiente de curtosis percentílico y la g-kurtosis, entre otros, los cuales se prestan para confusión si no se conoce la diferencia. Adicionalmente, se debe considerar el origen de los datos, debido a que la curtosis relaciona la media y la varianza de la distribución y esta última difiere si se trata de una población o de una muestra.
Coeficiente de curtosis (K)
La curtosis se puede estimar como la razón entre el cuarto momento alrededor de la media y el segundo momento elevado al cuadrado. Para efectos de este trabajo esto se puede expresar como:
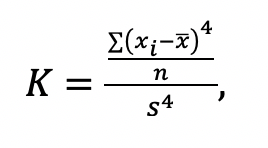 (3)
(3)
donde:
En este caso, si:

Claramente (3) se trata del coeficiente de curtosis para una distribución muestral, en el caso de tratarse de una población, en lugar de  debe emplearse μ y en lugar de
debe emplearse μ y en lugar de  Lo que haría que el valor del denominado cambie y por tanto el de K.
Lo que haría que el valor del denominado cambie y por tanto el de K.
Exceso de curtosis (EK)
El exceso de curtosis o grado de curtosis, es el coeficiente que mayoritariamente tiende a confundirse con la curtosis, quizás debido a la relación en su estimación y a que partir de ambos se puede llegar a la misma conclusión, siempre y cuando se tenga claro su diferencia, la distribución normal

tiene K=3, mientras que su EK=0 y este se expresa como:
(4)
en este caso, si:

Exceso de curtosis ajustado
El estimador muestral de la curtosis es sesgado cuando la muestra es pequeña. Byers (2000) demostró que para una muestra de tamaño n, el máximo valor de que β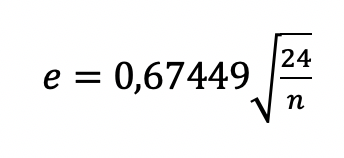 (definido en la ecuación (1)) puede tomar es
(definido en la ecuación (1)) puede tomar es 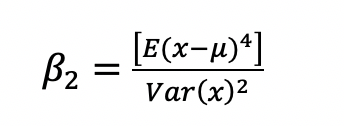 . Seier (2003) cita la versión ajustada la curtosis al tamaño de muestra:
. Seier (2003) cita la versión ajustada la curtosis al tamaño de muestra:
(5)
El concepto y la medición de la curtosis es más complejo de lo que parece y de lo que se muestra en la mayoría de los libros de texto de estadística y econometría. Para construir una medida de curtosis robusta para distribuciones asimétricas, Ruppert (1987) propone tomar la proporción de dos funcionales de escala robusta, por ejemplo, dos rangos interfráctiles. Unos años más tarde, el trabajo de Hosking (1990) introduce el concepto de L-momento y la L-kurtosis, que a diferencia de la curtosis es robusta a los valores atípicos, es recomendada en el análisis de señales de vibración y en investigación de recursos hídricos.
En el presente trabajo se hace énfasis en los procedimientos pertinentes a su estimación puntual, como se encuentra programado en la mayoría de los paquetes estadísticos, aunque no se puede dejar de mencionar que la robustez de estas medias ha sido cuestionada. El debate al respecto es muy extenso y no es objeto de este trabajo, solo se menciona una pequeña parte de todo el desarrollo en torno a este tema y se comenta la existencia de criterios más robustos, no solo para la custosis sino también para la asimetría. La media aritmética es sensible a valores extremos y, dado que la asimetría y la curtosis se basan esencialmente en promedios, también son sensibles a los valores atípicos. Kim y White (2003) comentan la poca atención a la falta de solidez de estas medidas en el campo financiero y mediante una aplicación al índice S&P500 demuestran que la afirmación como hecho estilizado de que los rendimientos del mercado de valores tienen una asimetría negativa y un exceso de curtosis puede haber sido aceptada con demasiada facilidad.
Metodología
Con el fin de estudiar las diferencias entre software en el resultado de la curtosis, se utilizaron dos series de datos. El primer juego de datos corresponde a un muestreo de tallos molederos de un ensayo de caña de azúcar, en el cual se seleccionaron de forma aleatoria 25 de 3200 metros
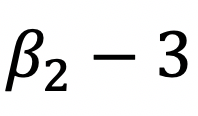
lineales de cultivo. El segundo grupo de datos, se trata de datos de costos de producción de leche (colones litro-1) para una muestra de 166 productores. Ambas muestras se obtuvieron de otras investigaciones. Adicionalmente, con el fin de estimar probabilidades empíricas fue necesario generar muestras aleatorias N~(100,625).
Los paquetes estadísticos empleados fueron de: Gretl 2018c, InfoStat 2018, Stata 12.0, R 3.5.1, Eviews 9, SAS v9, SPSS 25, Microsoft Excel 2016, además de la estimación directa mediante la aplicación de las ecuaciones (3), (4) y (5).
Resultados y discusión
En la Figura 3 se muestra la distribución de frecuencia de ambas muestras y en el Cuadro 1 la estadística descriptiva (omitiendo la curtosis).
Figura 3. Distribución de frecuencia de las dos muestras analizadas.
Cuadro 1. Estadística descriptiva de las dos muestras analizadas.



Variaciones en la medición
Empleando las ecuaciones (3), (4) y (5) se obtuvieron los resultados que se muestran en el Cuadro 2 y el Cuadro 3. Los datos empleados en este artículo corresponden a muestras, sin embargo, dado el objetivo de este trabajo, en algunos casos se hace omisión a ese hecho y se trabajan como si se tratara de poblaciones.
Cuando se trabajó con la muestra de tallos molederos (Cuadro 2), la diferencia entre emplear varianza muestral o varianza poblacional no repercute en los resultados tanto como lo hace el factor de ajuste. Los datos de tallos molederos corresponden a una muestra pequeña. Al emplear la fórmula sin ajuste por tamaño de la muestra, se concluye que se trata de una distribución más aplanada que la normal (platicúrtica), sin embargo, la conclusión cambia al incorporar el factor de ajuste para muestras pequeñas y por el contrario se afirma que la distribución es leptocúrtica. Este resultado contradictorio es un caso particular, por lo que mediante una simulación de mil muestras aleatorias de una distribución normal con 25 observaciones se estimó que existe aproximadamente un 20% de probabilidad de llegar a una conclusión contradictoria, como en el caso de la muestra de tallos molederos.
Cuadro 2. Curtosis y exceso de curtosis empleando varianza poblacional y muestral y el factor de ajuste en la muestra pequeña.
Cuando se utilizó la muestra grande (Cuadro 3), los resultados varían, sin embargo, no hubo diferencia en la conclusión, independientemente del tipo de varianza o si se empleó ajuste o no, en todos los casos se concluye que la distribución es leptocúrtica (K>3). Lo que se observa es que para muestras grandes:
(6)
Lo que gráficamente se puede apreciar en la Figura 4, las fórmulas convergen en tanto crece el tamaño de la muestra.
Cuadro 3. Curtosis y exceso de curtosis empleando varianza poblacional y muestral y el factor de ajuste en la muestra grande.
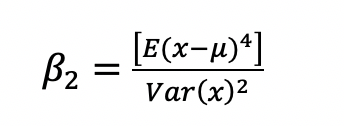


Figura 4. Tendencia del factor de ajuste según el tamaño de muestra.
Variaciones entre software
Se cargaron las dos muestras a los diferentes paquetes estadísticos y se realizó el cálculo del coeficiente de curtosis. En la mayoría de los casos la curtosis forma parte de los resultados de las estadísticas principales de una distribución y por lo general cada software arroja un único resultado.
En el Cuadro 4 se muestran los resultados para la muestra pequeña (tallos molederos). En gris se señala el valor que se obtuvo del software. Los paquetes: Gretl, InfoStat y Stata llegan a la misma conclusión y como se puede observar, estos paquetes trabajan con varianzas poblacionales por lo que no realizan ajuste.
Por su parte SAS, SPSS y Excel realizan el cálculo de exceso de curtosis ajustado para muestras pequeñas y en este caso, llegan a una conclusión diferente que los tres anteriores.
EViews y R son más versátiles y permiten estimar tres valores de exceso de curtosis, aunque les llaman curtosis, aquí dependerá del usuario qué valor requiera. R permite especificar entre: tipo 1 (poblacional, sin ajuste), tipo 2 (muestral, con ajuste) y tipo 3 (muestral, sin ajuste), sin embargo, si el usuario no especifica el tipo, R por defecto calcula el tipo 3.
De todos los programas evaluados, SPSS fue el único que por defecto arroja el valor del error estándar3 para este coeficiente, mediante la fórmula:
(7)
3El error estándar es una estimación de cuánto varía el valor de una estadística de prueba de muestra a muestra. Es una medida de la incertidumbre de la estadística de prueba. La razón de la kurtosis sobre su error estándar puede utilizarse como prueba de normalidad.


Cuadro 4. Estimación de la curtosis y exceso de curtosis para la muestra pequeña en los diferentes softwares.
Nota: En gris se señala el valor que se obtuvo del software.
Los resultados de la muestra de costos de producción de leche (muestra grande) se presentan en el Cuadro 5. A diferencia de lo que sucedió con la muestra pequeña, en este caso todos los softwares llegaron a la misma conclusión: la distribución es leptocúrtica, siempre K>3 y el EK>0. Esto confirma lo citado en la ecuación (6), cuando n tiende a infinito el efecto del factor de ajuste desaparece.
Cuadro 5. Estimación de la curtosis y exceso de curtosis para la muestra grande en los diferentes softwares.
Nota: En gris se señala el valor que se obtuvo del software.
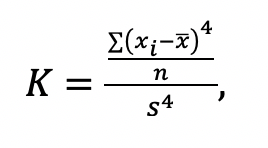

En el Cuadro 6 se sintetizan los resultados de este trabajo; en este se muestra el término que emplea cada software y el procedimiento que efectivamente realiza, en gris se muestran los casos donde no hay correspondencia entre término y procedimiento. Solamente Gretl y Stata son congruentes en este sentido.
InfoStat hace uso del término curtosis en el listado de medidas resumen cuando en realidad realiza el cálculo de exceso de curtosis y asumen varianza poblacional, por lo que no realiza ajustes de tamaño de muestra. Excel también hace uso incorrecto del término incluyendo curtosis en el listado de fórmulas, cuando lo que estima es exceso de curtosis; sin embargo, a diferencia de InfoStat, Excel asume que se trata de una muestra pequeña y aplica el factor de ajuste. En términos prácticos es preferible esto a asumir que se trata de una población puesto que, como se mencionó antes, los resultados suelen ser más sensibles a este ajuste que al tipo de varianza empleada. Los paquetes SAS y SPSS realizan el mismo procedimiento que Excel.
EViews y R, a diferencia de otros, dan la opción de estimar tres tipos de excesos de curtosis, aunque emplean el término curtosis. La ventaja de estos softwares es que permiten especificar si se trata de una población, si se trata de una muestra “pequeña” y por tanto debe considerarse el factor de ajuste en la estimación, o bien, si se trata de una muestra “grande” que no requiere ajuste.
Cuadro 6. Resumen de términos y procedimientos empleados por los softwares estadísticos.
Conclusiones
Para cualquier usuario de paquetes estadísticos es esencial la claridad del procedimiento empleado por el software, no solamente para realizar una correcta interpretación, también para juzgar cuál paquete emplear según las particularidades de cada caso; para este fin, en este trabajo se exponen las diferencias en la estimación del coeficiente de curtosis en algunos softwares de uso común para economista agrícolas.
Las diferencias entre software no implican errores de cálculo, el único error que se puede atribuir es el uso indiscriminado de los términos. La confusión que se puede generar es debido a que muchos paquetes no emplean de manera acertada el concepto de curtosis.
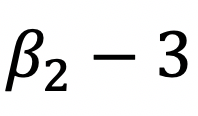
El factor de ajuste se diseñó para muestras pequeñas, por lo que en muestras grandes pierde significancia. Se estimó que existe aproximadamente un 20% de probabilidad de llegar a una conclusión equivocada al trabajar con muestras pequeñas y no considerar este ajuste. Por lo tanto, softwares como Gretl, InfoStat y Stata no son recomendables para la estimación de la curtosis cuando se trabaja con muestras pequeñas, en su lugar puede emplearse SAS, SPSS, Excel, Eviews o R. Estos últimos dos son los paquetes más completos en este tema de la curtosis, ofrecen al usuario la especificación de todos los escenarios que podrían presentarse (muestra grande, muestra pequeña sin ajuste y muestra pequeña con ajuste), pero a la vez exigen mayor capacitación para su uso, requiere que se domine el lenguaje de programación correspondiente y diferenciar entre los tipos de exceso de curtosis que estiman.
Al emplear cualquiera de los paquetes mencionados los resultados son correctos, solamente es necesario saber interpretarlos según lo que cada uno ofrece al usuario.
Literatura citada
Greene, W. H. (2011). Econometric Analysis. (7ed). Prentice Hall. 1241 p.
Byers, R. (2000). On the Maximum of the Standardized Fourth Moment. InterStat,1(2),1-7.
Fernández, S. F., Sánchez, J. M., Córdoba, A., Cordero, J. M., y Largo, A. C. (2002). Estadística descriptiva. ESIC Editorial. 566 p.
Finucan, H. M. (1964). A note on Kurtosis. Journal of the Royal Statistical Society, Series B, 26, 111-112. DOI: 10.1111/j.2517-6161.1964.tb00545.x.
Hosking, J. (1990). L-Moments: Analysis and estimation of distributions using linear combinations of order statistics. Journal of the Royal Statistical Society. Series B, 52(1), 105-124.
Kim, T. y White, H. (2003). On More Robust Estimation of Skewness and Kurtosis: Simulation and Application to the S&P500 Index. UC San Diego: Department of Economics, UCSD. Disponible en: https://escholarship.org/uc/item/7b52v07p
Mardia, K. V. (1970). Measures of Multivariate Skewness and Kurtosis with Applications. Biometrika, 57, 519-530. DOI: 10.2307/2334770.
Moors, J. (1988). A Quantile Alternative for Kurtosis. Journal of the Royal Statistical Society. Series D (The Statistician), 37(1), 25-32. DOI: 10.2307/2348376.
Person, K. (1905). Das Fehlergesetz und Seine Verallgemeinerungen durch Fechner und Pearson. A Rejoinder. Biometrika, 4(1/2), 169-212. DOI: 10.2307/2331536.
Ruppert, D. (1987). What is kurtosis? An influence function approach. The American Statistician, 41(1), 1-5. DOI: 10.2307/2684309.
Seier, E. (2003). Curtosis. PESQUIMAT, VI(2), 1- 26.
Student (1927). Errors of Routine Analysis. Biometrika, 19(1/2), 151-164. DOI: 10.2307/2332181.
Westfall, P.. (2014). Kurtosis as Peakedness, 1905-2014. RIP. The American Statistician, 68(3), 191-195. DOI:10.1080/00031305.2014.917055.