

e-Agronegocios
Revista electrónica publicada por el Centro de Investigación en Economía Agrícola y Desarrollo Agroempresarial, la Escuela de Economía Agrícola y Agronegocios y el Programa de Posgrado en Gerencia Agroempresarial de la Universidad de Costa Rica, 2060, San José, Costa Rica.
![]()
e-Agronegocios
Revista electrónica semestral, ISSN-2215-3462
Volumen 1, número 1, articulo 2
Enero-junio 2015
Publicado 1 de enero, 2015 https://sites.google.com/site/eagronegociosucr/
MODELO DE PROGRAMACIÓN LINEAL PARA MINIMIZAR EL COSTO DE FERTILIZACIÓN GRANULADA DE MACRO NUTRIMENTOS EN EL CULTIVO DE LA ZANAHORIA EN COSTA RICA
Javier Paniagua Molina
Javier Paniagua Molina1
Se empleó un modelo de programación lineal para minimizar el costo de la fertilización de nutrimentos mayores, N, P, K, Ca y Mg, con la finalidad de buscar mecanismos para mejorar la competitividad de cultivos hortícolas como la zanahoria.El costo mínimo obtenido fue de US$1.601,79 por hectárea, con el empleo de 714,19 kg/ha de 10-30-10, 1026,81 kg/ha de 15-3-31, 401,79 kg/ha de 15-15-15, 244,12 kg/ha de sulfato de magnesio y 525 kg/ha de carbonato de calcio. El rendimiento meta definido fue de 50 t/ha.Estos resultados contrastan con la fertilización tradicional en la zona bajo estudio, en donde predomina el uso de pocas fuentes fertilizantes.
Palabras claves: nutrición vegetal, investigación de operaciones, programación lineal, costos de producción agrícola, costos de fertilización
Fecha de recibido: 31 de julio del 2014 Fecha de aprobado: 28 de agosto del 2014 Fecha de corregido: 10de octubre del 2014
![]()
1 Profesor, investigador y consultor. javier.paniagua@ucr.ac.cr Escuela de Economía Agrícola y Agronegocios. CIEDA. Universidad de Costa Rica.
Linear programming model to optimize the cost of granulated macronutrients fertilization in carrot cropping in Costa Rica
A linear programming model was used to minimize the cost of higher nutrient fertilization, N, P, K, Ca and Mg, in order to seek ways to improve the competitiveness of horticultural crops like carrot cropping. The minimum cost obtained was US $ 1,601.79 per hectare, with the use of 714.19 kg /hec of 10-30-10, 1026.81 kg /hec of 15-3-31, 401.79 kg/hec of 15- 15-15, 244.12 kg /hec of magnesium sulfate and 525 kg /hec of calcium carbonate. The defined target yield was 50 t / hec. These results contrast with traditional fertilization in the area under study, where is common the use of a few source of fertilizers.
Keywords: plant nutrition, operations research, linear programming, agricultural cost, fertilization cost.
La programación lineal
La programación lineal, en palabras de Taha (2004) se aplica a modelos de optimización en los que las funciones objetivo y restricción son estrictamente lineales.
La técnica se aplica en una amplia variedad de casos, en los campos de la agricultura, industria, transporte, economía, salud, ciencias sociales y de la conducta y militar. También produce algoritmos eficientes de cómputo para problemas con miles de restricciones y variables.
En realidad, debido a su gran eficacia de cálculo, la programación lineal forma la columna vertebral de los algoritmos de solución para otros modelos de investigación de operaciones, como las programaciones entera, estocástica y no lineal.
Los modelos de programación lineal pueden ser utilizados para resolver problemas que involucran una o varias funciones objetivo. Cuando el problema de decisión envuelve una única función objetiva, la solución óptima puede ser calculada con simples algoritmos; cuando el problema encierra varios objetivos, una solución óptima se puede cuantificar utilizando modelos de optimización de criterios múltiples como programación por metas u objetivos, o enfoque interactivo de criterio múltiple (Romero and Rehman, 1989 c.p, Macowski, et al., 2001).
Para comprender el funcionamiento de la programación lineal, se debe entender el concepto de superposición, el cual establece que la respuesta de un sistema lineal resulta de varias entradas simultáneas y es igual a la suma de dichas respuestas de cada uno de los insumos entrantes (Dixon K.R. 2011).
Debido a esta naturaleza Hanssonet al. (1999) determinan que "La programación lineal (PL) es un método establecido para la determinación de las estrategias óptimas de fertilizantes en agricultura".
Según Ghosh et al. (2003), es probable que las aplicaciones de N–P–K a un nivel más alto que el requerido, puedan causar diversos efectos en los cultivos y por ende una disminución sustancial de sus rendimientos. Por lo tanto, para una plantación sostenible es necesario producir y aplicar óptimas combinaciones de nutrientes al suelo. Esto resulta en un incremento de la producción de cultivos, con un mayor beneficio-costo percibido y una mejora en la posición económica de los productores. Sin embargo, este punto de vista económico es uno de los que más se pasa por alto, debido al desbalance que muchas veces se da entre el plan de fertilización preparado por el asesor agrícola y el comportamiento de los productores con respecto al costo de los insumos.
En un artículo denominado Gestión de Granjas basado en Programación Matemática, de Žgajnar y Kavčič (2012), desarrollaron un trabajo de investigación, utilizando métodos de programación matemática, entre ellos la programación lineal, con el fin de demostrar un posible enfoque para un plan de fertilización, aceptable con las regulaciones y económicamente eficiente.
Ghosh et al. (2003) desarrollaron un trabajo basado en programación lineal, con el fin de obtener un planteamiento de combinaciones de fertilizantes óptimas en cultivos de arroz en Bengal (India); y se logró solucionar, por medio de un modelo, el mantenimiento de la fertilización del suelo, y por ende el aumento sustancial del rendimiento de arroz.
La programación lineal ha sido la base,en conjunto con otras técnicas, para desarrollar combinaciones óptimas de fertilizantes, en este caso el modelo abastece los nutrientes que el cultivo demanda, así como los costos razonables y la cantidad óptima de fertilizante que se debe aplicar (Hansson, et al., 1999).
En este sentido, Haankuku, Epplin y Kakani (2014), tuvieron como objetivo determinar el rendimiento del forraje de sorgo en respuesta al N, y el nivel óptimo de fertilizantes y los costos de producción por medio de un modelo de programación lineal entre otros ajustes matemáticos.
Por otra parte Brino y Rezende (2012), estudiaron la minimización del costo de reactivos de alta pureza en experimentos con plantas con déficit nutricionales, con el fin de optimizar la cantidad faltante mediante modelos de programación lineal, y finalmente generar tablas de recomendación para la posterior preparación de soluciones efectivas. Se concluyó que los modelos formulados eran capaces de reducir los costos de adquisición de los reactivos.
Rendimientos y absorción de nutrimentos en zanahoria
En Costa Rica el rendimiento de zanahoria varía dependiendo del híbrido de que se trate, Richmond y Méndez (2010) señalan que los híbridos más utilizados son Bolero F1 y Bangor F1, y citan que para el año 2007, la Agencia del Ministerio de Agricultura y Ganadería en Pacayas de Cartago registró rendimientos de 52,6 a 78,9 toneladas por hectárea para el distrito de Alvarado y de 65,7 t/ha en el distrito de Cipreses para el híbrido Bangor F1.
Ortiz y Amado (2004) citados por Sosa et al. (2013), indican que cuando se utilizan híbridos en combinación con una fecha de siembra óptima y un programa de fertilización balanceada, en México es posible obtener cerca de 70 toneladas por hectárea de zanahoria comercial.
Sosa et al. (2013), en híbrido Concerto, obtuvieron un rendimiento total de zanahoria medido en 74,3 t/ha, equivalente a un rendimiento comercial de 64 t/hay para lograrlo el cultivo absorbió 206, 36.6 y 254,2 kg/ha de N, P y K, respectivamente, lo que equivale a 3,2, 0,57 y 3,97 kg/ha por tonelada de rendimiento comercial. Estos resultados son levemente menores a lo reportado por Bertsch (2009) quien señala que para la producción de una tonelada de zanahoria, el cultivo absorbe en promedio 4, 0,8 y 6 kg/ha de N, P y K, respectivamente.
Adicionalmente, la absorción de calcio y magnesio se puede deducir de los datos de Bertsch (2009) en 3 y 0,4 kg/ha respectivamente para producir una tonelada de zanahoria comercial.
Richmond y Méndez (2010) determinaron en Cot de Cartago, a una altitud de 1921 msnm, un rendimiento para el híbrido Bangor F1 de 80,89 t/ha de producto fresco y de 64,17 t/ha de producto comercial.
Este trabajo de investigación seacerca al realizado por Campaña (2011) en el caso del cultivo de papa, quien determinó la combinación óptima que minimizó el costo de la fertilización en ese cultivo.
El objetivo de esta investigación es encontrar, mediante programación lineal, la combinación de fertilizantes que minimicen el costo de nutrición de la zanahoria para un determinado rendimiento objetivo definido en 50 toneladas por hectárea de producto comercial.
La programación lineal, tal como se aplica en la planificación agrícola, y en palabras de Igwel y Onyenweaku1 (2013), representa un método sistemático para determinar matemáticamente un plan óptimo para elecciones y combinaciones óptimas dentro de las empresas agrícolas, a fin de maximizar los ingresos o reducir al mínimo los costos dentro de los límites de los recursos agrícolas disponibles.
El modelo formal de programación lineal se define de la siguiente forma: Maximizar o minimizar la función objetivo Z:
m
Z Ci X j
j 1
(1)
Sujeto a una serie de restricciones:
n
m
aij X j
j1
,,
bj
i1
(2)
X j 0 para todo j (restricción de no negatividad)
El algoritmo de solución del sistema anterior, empleado por el software seleccionado, es el método simplex de interacción múltiple.
Datos
Se procedió a recolectar datos de varias cotizaciones de fertilizantes mayormente utilizados por los agricultores de las zonas de Cartago, Costa Rica, dedicadas al cultivo de zanahoria, abarcando las zonas de Cot y Oreamuno.
El rendimiento comercial objetivo se definió en 50 toneladas por hectárea y se aplicó la absorción meta por tonelada recomendada por Bertsch (2009). No se trabajó con el rendimiento reportado por Richmond y Méndez (2010) de 64 t/ha, puesto que se considera adecuado sensibilizar el rendimiento para condiciones más heterogéneas típicas de las fincas de los productores de la zona de estudio.
El modelo se propone para suelos andisoles de textura franca o franco arenosa, que dado su origen volcánico posee presencia de arcillas alofanas que fijan alta cantidad de fósforo. Esto implica entonces emplear las eficiencias recomendadas por Bertsch (2009) para la fertilización en este tipo de suelos, de 70% para nitrógeno, 30% para fósforo y 80% tanto para potasio, calcio como para magnesio.
Procesamiento de la información
El modelo se ajustó con ayuda del software QM for Windows, versión 4.0, desarrollado por Howard Weiss para fines didácticos y que se basa en el algoritmo de cálculo subyacente que es el método simplex.
Demanda y oferta de nutrimentos
La tabla 1 muestra la estimación de la demanda nutricional para un rendimiento comercial objetivo de 50 t/hade zanahoria.
Tabla 1
Demanda nutricional de macronutrimentos para un rendimiento de 50 t/ha de zanahoria
-------------------------- kg -----------------------------------
N | P | K | Ca | Mg | |
Absorción (kg): rendimiento 1000 | 4,00 | 0,80 | 6,00 | 3,00 | 0,40 |
Absorción (kg): rendimiento 50000 | 200,00 | 40,00 | 300,00 | 150,00 | 20,00 |
Eficiencia: | 70,00% | 30,00% | 80,00% | 80,00% | 80,00% |
Absorción eficiente (kg): | 285,71 | 133,33 | 375,00 | 187,50 | 25,00 |
N | P2O5 | K2O | CaO | MgO | |
Factor de conversión | 1 | 2,29 | 1,2 | 1,4 | 1,66 |
Demanda nutricional (kg/ha) | 285,71 | 305,33 | 450,00 | 262,50 | 41,50 |
Demanda nutricional (kg/tonelada) | 5,71 | 6,11 | 9,00 | 5,25 | 0,83 |
Fuente: elaboración propia con base en Bertsh (2009) y un rendimiento objetivo definido en 50 t/ha
La demanda nutricional para lograr un rendimiento de 50 toneladas por hectárea, representa la dosis de fertilizante necesaria en el sistema bajo estudio, para el caso del nitrógeno representó 285,71 kg/ha, para fósforo 305,83 kg/ha y para potasio 450 kg/ha.
Tencio (2013) reporta el uso de 1000 kg de 10-30-10 para fertilizar la zanahoria en la zona de Cartago, lo cual implica un aporte de 100 kg/ha de N, 300 kg/ha de P2O5 y 100 kg/ha de K2O para un rendimiento de 35 t/ha. Estos datos difieren de los estimados en este trabajo en donde se pretende un rendimiento objetivo mayor e igual a 50 t/ha.
La investigación de mercado realizada permitió elaborar la tabla 2 en donde se presentan los fertilizantes más comunes ofrecidos en la zona bajo estudio y de fácil disponibilidad al productor, con su respectivo porcentaje de aporte nutricional y su costo para el productor.
Solo se considera el aporte de los macronutrimentos nitrógeno, fósforo, potasio, calcio y magnesio, por ser los que se suministran de forma granulada y en mayor cantidad. Cualquier aporte de elementos menores queda fuera del alcance de este estudio.
Tabla2
Aporte nutricional y costo de los fertilizantes ofrecidos en la zona de estudio
![]()
Variable Fertilizante N P O K O CaO MgO Costo
Costo
2 5 2
(¢/kg)
(US$/kg)
X1 | 10-30-10 | 10,0% | 30,0% | 10,0% | 0,0% | 0,0% | 368,00 | 0,669 |
X2 | 12-24-12 | 12,0% | 24,0% | 12,0% | 0,0% | 0,0% | 359,67 | 0,654 |
X3 | Nutrán | 33,5% | 0,0% | 0,0% | 0,0% | 0,0% | 276,67 | 0,503 |
X4 | 15-3-31 | 15,0% | 3,0% | 31,0% | 0,0% | 0,0% | 375,89 | 0,683 |
X5 | 18-5-15-6-0,2 | 18,0% | 5,0% | 15,0% | 0,0% | 6,0% | 368,56 | 0,670 |
X6 | 19-4-19 | 19,0% | 4,0% | 19,0% | 0,0% | 0,0% | 370,33 | 0,673 |
X7 | 12-27-8 | 12,0% | 27,0% | 8,0% | 0,0% | 0,0% | 411,78 | 0,749 |
X8 | 15-3-20 | 15,0% | 3,0% | 20,0% | 0,0% | 0,0% | 360,22 | 0,655 |
X9 | 15-24-12 | 15,0% | 24,0% | 12,0% | 0,0% | 0,0% | 363,00 | 0,660 |
X10 | 15-15-15 | 15,0% | 15,0% | 15,0% | 0,0% | 0,0% | 320,56 | 0,583 |
X11 | Sulfato de potasio | 0,0% | 0,0% | 50,0% | 0,0% | 0,0% | 683,60 | 1,243 |
X12 | Nitrato de calcio | 15,0% | 0,0% | 0,0% | 26,0% | 0,0% | 351,40 | 0,639 |
X13 | Fosfato monoamónico (MAP) | 11,0% | 52,0% | 0,0% | 0,0% | 0,0% | 1.113,20 | 2,024 |
X14 | Fosfato monopotásico (MKP) | 0,0% | 52,0% | 34,0% | 0,0% | 0,0% | 1.186,00 | 2,156 |
X15 | Nitrato de potasio | 13,0% | 0,0% | 44,0% | 0,0% | 0,0% | 919,60 | 1,672 |
X16 | Sulfato de magnesio | 0,0% | 0,0% | 0,0% | 0,0% | 17,0% | 260,00 | 0,473 |
X17 | Carbonato de calcio | 0,0% | 0,0% | 0,0% | 50,0% | 0,0% | 76,33 | 0,139 |
X18 | Urea | 46,0% | 0,0% | 0,0% | 0,0% | 0,0% | 377,78 | 0,687 |
Fuente: consulta a negocios comercializadores de insumos agrícolas, Cartago, julio 2014.
Planteamiento del problema
El modelo se plantea con 18 variables, una función objetivo y 5 restricciones. Las siguientes ecuaciones permiten plantear el problema a resolver de forma algebraica:
Z 0,669X1 0,654X 2
0,503X 3 0,683X 4
0,670X 5 0,673X 6
..
.. 0,749X7
0,655X 8 0,660X 9
0,583X10 1,243X11 0,639X12 ..
.. 2,024X13 2,156X14 1,672X15 0,473X16 0,139X17 0,687 X18
(3)
Nitrógeno
0,1X1 0,12X 2 0,335X 3 0,15X 4 0,18X 5 0,19X 6 0,12X 7 0,15X 8 ..
.. 0,15X 9 0,15X10 0,15X12 0,11X13 0,13X15 0,46X18 285,71
Fósforo
0,3X1 0,24X 2 0,03X 4 0,05X5 0,04X 6 0,27 X 7 0,03X8 0,24X 9 ..
.. 0,15X10 0,52X13 0,52X14 305,33
(4)
Potasio
0,1X1 0,12X 2 0,31X 4 0,15X 5 0,19X 6 0,08X 7 0,2X 8 0,12X 9 ..
.. 0,15X10 0,50X11 0,34X14 0,44X15 450
(5)
Calcio
0,26X12 0,50X17 262,50
(6)
(7)
Magnesio
0,06X 5
0,17 X16
41,50
(8)
Restricción de no negatividad
X j 0
, j 1,2,. ,18
(9)
Resolución del modelo
La tabla 3 muestra el resultado de la combinación óptima que minimiza los costos de fertilización para el cultivo, luego de 10 interacciones del método simplex.
Tabla 3
Resultados del modelo de programación lineal aplicado
Variable Status Value
X1 | Basic | 714,1874 |
X2 | NONBasic | 0 |
X3 | NONBasic | 0 |
X4 | Basic | 1026,813 |
X5 | NONBasic | 0 |
X6 | NONBasic | 0 |
X7 | NONBasic | 0 |
X8 | NONBasic | 0 |
X9 | NONBasic | 0 |
X10 | Basic | 401,7957 |
X11 | NONBasic | 0 |
X12 | NONBasic | 0 |
X13 | NONBasic | 0 |
X14 | NONBasic | 0 |
X15 | NONBasic | 0 |
X16 | Basic | 244,1176 |
X17 | Basic | 525 |
X18 | NONBasic | 0 |
artfcl 1 | NONBasic | 0 |
artfcl 2 | NONBasic | 0 |
artfcl 3 | NONBasic | 0 |
artfcl 4 | NONBasic | 0 |
artfcl 5 | NONBasic | 0 |
Optimal Value (Z) $1.601,79
El costo variable mínimo obtenido por uso de fertilizantes fue de US$1.601,79 por hectárea. En la figura 1 se muestrala distribución del consumo de fertilizantes con una combinación de 714,19 kg/ha de 10-30-10, 1026,81 kg/ha de 15-3-31, 401,79 kg/ha de 15- 15-15, 244,12 kg/ha de sulfato de magnesio y 525 kg/ha de carbonato de calcio.
Estos resultados contrastan con la fertilización tradicional en la zona bajo estudio en donde predomina el uso de pocas fuentes de fertilizantes fosforados y fórmulas completasen lugar de incluir más fuentes que disminuyan el costo de fertilización.
Figura1
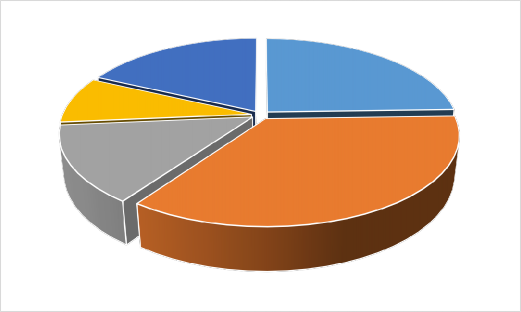
Distribución del consumo de fertilizantes para optimización del costo variable de su uso
Sulfato de magnesio 8%
Carbonato de calcio 18%
10-30-10
25%
15-15-15
14%
15-3-31
35%
El modelo de programación lineal permitió obtener una combinación óptima de fertilizantes, es decir, se determinó el costo mínimo de fertilizaciónque garantiza los requerimientos nutricionales del cultivo para el rendimiento objetivo fijado.
Los resultados muestran una combinación de fertilizantes que no corresponde con la empleada por el productor, lo cual le permite contar con opciones de mejora en cuanto a rendimiento y economía de recursos en las fincas hortícolas de la zona.
Es necesario afinar este tipo de estudio a un nivel más específico de finca, por lo que se considera adecuado planear investigación en sitio mediante diseños experimentales factoriales que incluyan el componente económico.
El alcance del trabajo se limitó a suplir los requerimientos nutricionales generales del cultivo, fuera de alguna fertilización correctiva al suelo o encalado para corrección de acidez. Este tipo de estudios puede mejorarse incluyendo fertilizaciones correctivas, encalado, nutrición foliar, enmiendas orgánicas y balance nutricional para elementos menores también.
Un agradecimiento especial a la empresa Agroindustrias Hortícolas de Costa Rica S.A., por su colaboración al permitir la visita a sus plantaciones de zanahoria en la zona de Cartago.
Agradecimiento al Centro de Investigación en Economía Agrícola y Desarrollo Agroempresarial, de la UCR, por apoyar la investigación aplicada de métodos cuantitativos en cultivos agrícolas.
Berstch, F. (2009) Absorción de nutrimentos por los cultivos. San José, Costa Rica, ACCS
Brino, M., y Rezende, L. (2012). Use of lineal programming models in experimentation with plant nutrients.19 (2), 255-261. Recuperado de http://www.scielo.br/scielo.php?pid=S0104-77602013000200009&script=sci_arttext
Campaña, D.F. (2011) Modelo matemático de programación lineal para optimizar la selección de fertilizantes a través de la disminución de los costos en el cultivo de la papa.Tesis de maestría, Escuela Politécnica Nacional. Recuperado de http://bibdigital.epn.edu.ec/bitstream/15000/7763/1/CD-3893.pdf
Dixon, K.R. (2011). Modeling and Simulation in Ecotoxicology with Applications in MATLAB and Simulink. Recuperado de http://www.crcnetbase.com.ezproxy sibdi.ucr.ac.cr:2048/doi/abs/10.1201/b11089-3?queryID=
Ghosh, D., Sharma, D.A., y Mattison, D.M. (2003). Goal programming formulation in nutrient management for rice production in West Bengal.International Journal of Production Economics. 95 (2005)1-7
Haankuku, C., Epplin, F.M., y Kakani, Y.G. (2014). Forage Sorghum Response to Nitrogen Fertilization and Estimation of Production Cost. Agronomy Journal 106 -5.
Hansson, P., Svensson, F., Hallefalt, B., y Diedrichsc, H. (1999). Nutrient and cost optimization of fertilizing strategies for Salix including use of organic waste products.Biomass and Bioenergy 17 (1999) 377-387
Igwel, K.C. y Onyenweaku1, E.C. (2013).A Linear Programming Approach to Food Crops and Livestock Enterprises Planning in Aba Agricultural Zone of Abia State, Nigeria. American Journal of Experimental Agriculture 3(2): 412-431
Mackowski, D. Hendrix, E., Van Ittersum, M.K., y Rosing, W.H., (2001). Generation and Presentation of nearly optimal solutions for mixed-integerlineal programming, applied to a case in farming system design. EuropeanJournal of OperationsResearch, 132(2001) 425- 428.
Paniagua (2013) Optimización del costo de fertilización con macronutrientes mediante programación lineal: el caso de la papa en la zona norte de Costa Rica. I Congreso en Economía Agrícola y Agronegocios y II Jornadas de Investigación del CIEDA. Recuperado de http://www.economiagricola.ucr.ac.cr/images/Congresos_Conferencias/Miercoles%2016%20Oct% 20(Mesa%201)/Optimizacion%20economica%20del%20costo%20de%20nutricion%20con%20mac roelementos%20por%20metodos%20cuantitativos_Javier%20Paniagua.pdf
Richmond, F. y Méndez, C. (2010). Rendimiento de 12 híbridos comerciales de zanahoria (Daucus carota L.) en el campo y en la planta de empaque. Agronomía Mesoamericana, 21(1), 167-176.
Sosa, A.; Ruiz, G.; Bazante; I.; Mendoza, A., Etchevers, J.D.; Padilla, J. y Castellanos J.Z. (2013). Absorción de nitrógeno, fósforo y potasio en zanahoria (Daucus carota L.) cultivada en el Bajío de México. IAH, (11), 27-30.
Taha, H.A. (2004). Investigación de Operaciones .Pearson Educación
Tencio (2013) Estructuras de costos de producción de hortalizas. Ministerio de Agricultura y Ganadería, Dirección Regional Central Oriental, p. 5.
Žgajnar, J. y Kavčič, S. (2012). Farm management support based on mathematical programming; an example of fertilization planning. Agroeconomia Croatica 2:2012(1)8-15. Recuperado de http://hrcak.srce.hr/index.php?show=clanak&id_clanak_jezik=139118&lang=en