

Revista electrónica publicada por el Centro de Investigación en Economía Agrícola y Desarrollo Agroempresarial, la Escuela de Economía Agrícola y Agronegocios y el Programa de Posgrado en Gerencia Agroempresarial de la Universidad de Costa Rica, 2060, San José, Costa Rica.
![]()
gronegocios
Revista electrónica semestral, ISSN-2215-3462
Volumen 2, número 2, articulo 4 Julio - Diciembre 2016 Publicado 1 de julio, 2016
https://sites.google.com/site/eagronegociosucr/
ESTIMACIÓN DEL EFECTO DE LA PENDIENTE SOBRE EL VALOR DE LA TIERRA EN LA ZONA DE LA DAMITA, CAÑÓN DEL GUARCO, POR MEDIO DEL MÉTODO ECONOMÉTRICO DE VALUACIÓN
Javier Paniagua Molina
Javier Paniagua Molina1
Se realizó investigación en la zona de Cañón del Guarco, provincia de Cartago, para determinar el efecto de la pendiente sobre el valor de mercado de la tierra.
Una muestra fue seleccionada de tal forma que se tuviera variabilidad en cuanto a pendiente y tamaño de las tierras.
Un modelo económetrico fue seleccionado y ajustado para medir la relación entre las variables y se obtuvo resultados significativos para la pendiente y el tamaño de la tierra como variables explicativas del valor de la tierra.
Palabras clave: Valoración de tierras, pendiente de terrenos, modelo econométrico
Fecha de recibido: 2 junio del 2016 Fecha de aprobado: 20 de junio del 2016 Fecha de corregido: 30 de junio del 2016
![]()
1Economista Agrícola, Master en Administración y Dirección de Empresas con énfasis en Finanzas, docente Escuela de Economía Agrícola y Agronegocios, Universidad de Costa Rica, San José. Investigador Centro de Investigación en Economía Agrícola y Desarrollo Agroempresarial CIEDA. javier.paniagua@ucr.ac.cr
Estimating the effect of slope on the land value in the area of La Damita, Guarco Canyon, by means econometric valuation method
Research was conducted in the area of Canyon del Guarco, Cartago, to determine the effect of the slope above the market value of the land.
A sample was selected so that variability in slope and size of the land had.
An econometric model was selected and adjusted to measure the relationship between variables and significant results were obtained for the slope and size of the land as explanatory variables the value of the land.
Key words: Land valuation, land slope, econometric models
Terrenos con una pendiente más pronunciada implica mayores costos de manejo ya sea tanto para usos agrícolas, industriales o residenciales. En el caso de actividades agrícolas a mayor pendiente mayores costos de labores, mientras que en otros usos, se requiere inversión para la nivelación correspondiente (Caballer, 1993)
Una adecuada asignación de recursos en el crédito rural implica considerar este factor para castigar el valor de un terreno conforme aumenta su pendiente y de esta forma refleje el valor que el mercado asigna en caso de liquidación del terreno como garantía crediticia.
En la zona de La Damita, fue posible encontrar referencias de mercado con distintos grados de pendiente de terrenos en un radio relativamente pequeño y de fácil acceso, lo que justificó el desarrollo de esta investigación.
El objetivo de este trabajo es determinar el efecto que ejerce la pendiente de un terreno sobre el valor de mercado del mismo, bajo condiciones de homogeneidad en otras variables explicativas del valor de la tierra.
Gurajti y Porter (2010) y Green (1994) indica que un modelo econométrico es aquel en donde una variable dependiente es explicada por una serie de variables independientes de acuerdo a lo siguiente:
Y 0 1 X 1 2 X 2 ... k X k û
Donde: cada beta corresponde a los coeficientes de regresión para cada una de las variables hasta la k-ésima variable influyente en el modelo y û corresponde a los residuos o errores de cada observación del modelo.
Son numerosos los trabajos que optan por los modelos econométricos para la estimación del valor de terrenos como los trabajos de Wise y Dover (1974), Sandrey et al. (1982), Capozza y Helsley (1989), Palmquist y Danielson (1989), Mendelsohn et al. (1994), Roka y Palmquist (1997), McDonald y McMillen (1998), Stewart y Libby (1998), Calatrava y Cañero (2000), Plantinga y Millar (2001) y Perry y Robison (2001).
Buitriago (2007) indica que la pendiente y el tamaño de un terreno son variables fundamentales para la determinación de su valor, en lo cual coinciden Palmquist y Danielson (1989) sobre todo porque argumentan que la pendiente influye en la erosión de los suelos, y por ende en su valor para generar beneficios.
Dado que no todos los terrenos tienen una misma área, el tamaño es siempre una variable obligada en cualquier estudio estadístico en el campo de la valoración de tierras. Cuales otras variables incluir en el modelo dependerán de que tan homogéneas sean las observaciones.
En el caso bajo estudio, la muestra obtenida corresponde a observaciones de valores de terrenos muy homogéneos entre sí en cuanto a distancia a centro de desarrollo, acceso, grado de desarrollo y servicios. Los terrenos muestreados presentaron variabilidad principalmente en cuanto a tamaño y pendiente, observaciones atípícas fueron eliminadas.
Para esta investigación, se definieron las siguientes variables:
Precio (P): precio de oferta de la tierra en colones por metro cuadrado
Pendiente (S): grado de inclinación promedio del terreno estimado en campo, medida como fracción
Tamaño (T): es el tamaño del terreno medido en metros cuadrados
Con el modelo ajustado, se estimó posteriormente el valor para dos terrenos seleccionados, uno plano y otro con un grado de inclinación fuerte, así mismo se generó una simulación del efecto pendiente a diferentes tamaños de terreno.
.
Ajuste del modelo
En la tabla 1 se presenta el resultado del análisis de regresión para las variables transformadas de manera adecuada.
Tabla 1. Resultados del modelo de regresión
Modelo MCO, usando las observaciones (T = 16) Variable dependiente: l_Valor_unitari
Coeficiente | Desv. Típica | Estadístico t | Valor p | ||
const | 12,2803 | 0,429018 | 28,6242 | <0,00001 | *** |
Pendiente | -1,43443 | 0,336029 | -4,2688 | 0,00091 | *** |
l_Area m_ | -0,407035 | 0,0540209 | -7,5348 | <0,00001 | *** |
Media de la vble. dep. | 8,381554 | D.T. de la vble. dep. | 0,796894 |
Suma de cuad. residuos | 0,688698 | D.T. de la regresión | 0,230167 |
R-cuadrado | 0,927700 | R-cuadrado corregido | 0,916577 |
F(2, 13) | 83,40354 | Valor p (de F) | 3,84e-08 |
Log-verosimilitud | 2,461310 | Criterio de Akaike | 1,077380 |
Criterio de Schwarz | 3,395146 | Crit. de Hannan-Quinn | 1,196068 |
rho | 0,015240 | Durbin-Watson | 1,921270 |
Los resultados muestran consistencia robusta desde el punto de vista estadístico ya que se obtuvo un R² igual a 92,70%, y las pruebas de hipótesis para los coeficientes de regresión resultaron significativas a los más bajos niveles de significancia del 1% y 5%, lo cual indica que hay relación estadística entre las variables.
El estadístico de Durbin-Watson obtenido fue de 1,92127 con una probabilidad asociada de p = 0,357264, lo que indica que no hay presencia de autocorrelación de primer orden en los datos.
Por su parte la prueba Breusch-Godfrey (BG), cuyo resultados se muestran en la tabla siguiente, indica que no hay autocorrelación para órdenes superiores, al menos hasta el cuarto rezago.
Tabla 2. Contraste Breusch-Godfrey de autocorrelación hasta el orden 4
Coeficiente Desv. Típica Estadístico t Valor p
---------------------------------------------------------------------
const | 0,0984763 | 0,441993 | 0,2228 | 0,8287 | |
Pendiente | 0,219132 | 0,371550 | 0,5898 | 0,5698 | |
l_Area m_ | -0,0175077 | 0,0562332 | -0,3113 | 0,7626 | |
uhat_1 | -0,154314 | 0,331775 | -0,4651 | 0,6529 | |
uhat_2 | -0,134051 | 0,291565 | -0,4598 | 0,6566 | |
uhat_3 | -0,560550 | 0,282830 | -1,982 | 0,0788 | * |
uhat_4 | -0,372020 | 0,355578 | -1,046 | 0,3227 |
R-cuadrado = 0,357556
Estadístico de contraste: LMF = 1,252253, con valor p = P(F(4,9) > 1,25225) = 0,356
Estadístico alternativo: TR^2 = 5,720902,
con valor p = P(Chi-cuadrado(4) > 5,7209) = 0,221
Ljung-Box Q' = 6,44155,
con valor p = P(Chi-cuadrado(4) > 6,44155) = 0,169
La prueba de heterocedasticidad de Breusch-Pagan permite rechazar la hipótesis nula de varianza no homogénea, de manera que se concluye que no hay heterocedasticidad en los datos, de acuerdo con Breusch y Pagan (1979).
Los resultados se muestran en la siguiente tabla:
Tabla 3. Contraste de heterocedasticidad de Breusch-Pagan Coeficiente Desv. Típica Estadístico t Valor p
-----------------------------------------------------------------------------------------
const | -1,84603 | 2,71798 | -0,6792 0,5089 |
Pendiente | -0,589400 | 2,12886 | -0,2769 0,7862 |
l_Area m_ | 0,345467 | 0,342241 | 1,009 0,3312 |
Suma de cuadrados explicada = 2,45618 Estadístico de contraste: LM = 1,228089,
con valor p = P(Chi-cuadrado(2) > 1,228089) = 0,541158
La siguiente figura muestra el patrón de los residuos û en donde es posible notar que se presenta la dispersión necesaria como para respaldar los resultados de las pruebas estadísticas realizadas.
0,4
0,3
0,2
0,1
residuo
0
-0,1
-0,2
-0,3
-0,4
-0,5
Residuos de la regresión (= l_Valor_unitari observada - estimada)
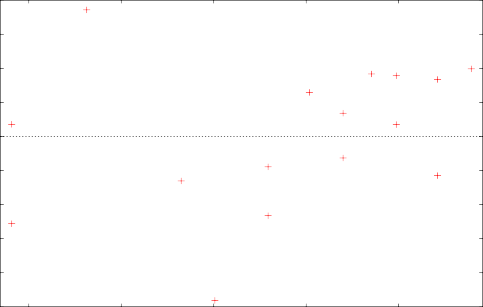
7 7,5 8 8,5 9
l_Valor_unitari
N
Figura 2. Residuos de la regresión mostrado un patrón disperso deseado
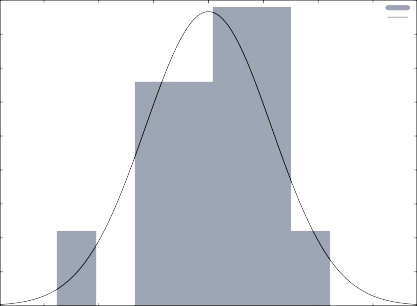
1,8
1,6
Estadístico para el contraste de n Chi-cuadrado(2) = 1,334 [0,5133
uhat2 (-2,2204e-016 0,23017)
1,4
ormalidad:
]
1,2
Densidad
1
0,8
0,6
0,4
0,2
0
-0,6 -0,4 -0,2 0 0,2 0,4 0,6
uhat2
Figura 3. Residuos de la regresión mostrado un patrón de distribución normal deseada
La figura anterior, muestra la cercanía de los residuos a la normalidad deseada para poder aplicar las pruebas estadísticas anteriores.
Dado que el modelo econométrico es apto para pronosticar debido a que no posee heterocedasticidad ni autocorrelación crónica, así también los residuos siguen una distribución de probabilidad normal, es posible aplicarlo al caso bajo estudio.
Uso del modelo
En la siguiente figura se muestra la localización de los terrenos a valorar en una hoja cartográfica a escala 1:50.000 ya que para este momento no fue conseguir una escala menor como 1:10.000 o 1:5.000.
El montaje realizado a escala, indica que la distancia vertical promedio entre curvas de nivel contiguas es de 30 metros y dado que existe una cota de 20 m de diferencia altitudinal entre cada curva, la pendiente promedio se calcula de la siguiente forma:
![]()
![]()
m y 100 20 100 67,7%
x 30
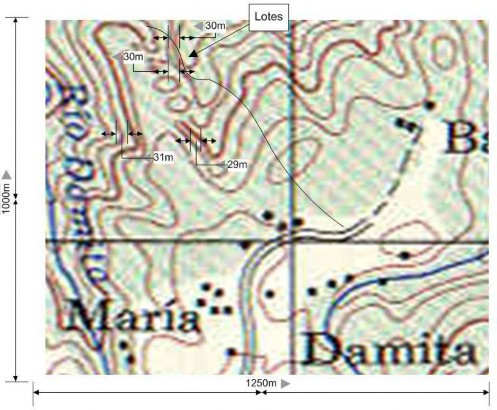
Figura 4. Topografía del lugar donde están los lotes, montaje con base en la Hoja Tapantí
El modelo econométrico predice que el valor de un terreno con un área de 1.500 m², toralmente plano, con acceso de lastre, servicio de agua potable y electricidad, localizado en los alrededores de La Damita, es de ¢10.977,06/m².
Aplicando el modelo econométrico obtenido a un terreno con una pendiente de 67,7%. y un tamaño de 1.500 m², y condiciones de servicios y acceso homogéneas, el obtiene un valor base de ¢4.156,60/m². Es notorio el efecto fuerte que ejerce la pendiente sobre la disminución de valor de la tierra.
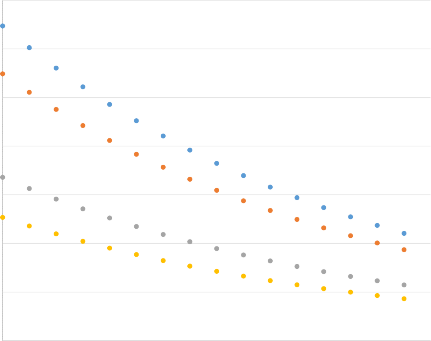
Las siguiente figuras mientras los resultados de la simulación del modelo para tamaños de 1.000, 1500, 5.000 y 10.000 m² con pendientes de desde 0% a 75% a intervalos de
incrementos de 5%.
¢14.000,00
¢12.000,00
¢10.000,00
Valor / m²
¢8.000,00
¢6.000,00
¢4.000,00
1.500 m²
1.000 m²
¢2.000,00
5.000 m²
10.000 m²
¢0,00
0% 10% 20% 30% 40% 50% 60% 70% 80%
Pendiente
Figura 4. Efecto de la pendiente sobre el valor de la tierra a diferentes tamaño de terrenos
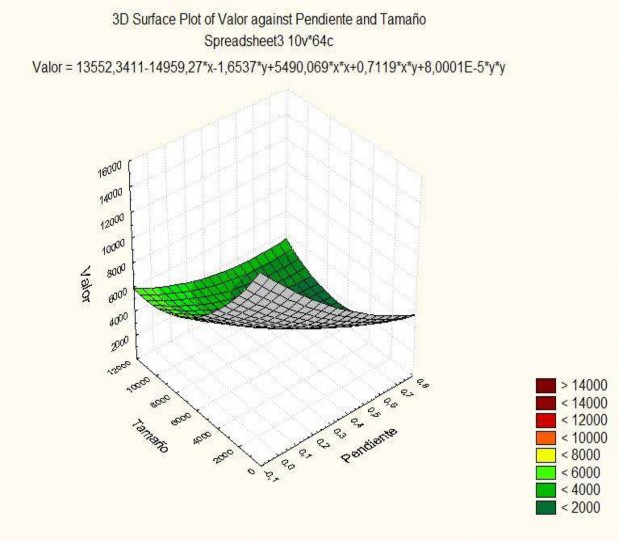
Figura 5. Efecto de la pendiente y el tamaño sobre el valor de la tierra
Se encontró evidencia estadística para confirmar que la pendiente de un terreno y su tamaño afectan su valor de mercado.
La pendiente sigue un modelo exponencial con un parámetro de regresión de -1,43 midiendo la pendiente en fracción, mientras que el tamaño de la tierra sigue un modelo potencial con un parámetro de regresión de -0,40.
De acuerdo con el estudio realizado, es de esperar con un 95% de confianza estadística, que un valor base para un lote de cerca de 1.500 m², con servicios, frente calle lastreada, con topografía del 67,7% y homogeneidad en todo lo demás, oscilará cerca de los ¢4.156,60/m² y si fuera plano, ese valor es de esperar que sea de ¢10.977,06/m².
Alonso, R, Serrano, A. (1998). Valoración Agraria. Casos Prácticos de Valoración Agraria.
Agrícola Española, Madrid.
Alonso, R., Iruretagoyena, M. T. (1990). Casos prácticos de Valoración Agraria. Ministerio de Agricultura Pesca y Alimentación, Madrid.
Arriaza, M.; Cañas Madueño, J.A. y Fernández Sánchez, J.I. (2002). “Valoración de fincas agrarias en la comarca de Pedroches (Córdoba)”. I Congreso Internacional de Valoración y Tasación. Valencia, 3-5 julio.
Bowerman, B.L. y O’Connell, R.T. (1990). Linear statistical models: an applied approach.
Duxbury.
Belmont, CA. Breusch, T. y Pagan, A. (1979). “A simple test for heteroscedasticity and random coefficient variation”. Econometrica, 47: 1287-1294.
Buitrago (2007). Factores determinantes del precio de la tierra rural en los municipios contiguos a Bogotá D.C. Cali, Colombia: Programa Editorial Universidad del Valle.
Caballer, V. (1993). Valoración agraria teoría y práctica. Mundi-Prensa, Madrid. Caballer, V., (1999). Valoración de Árboles. Mundi Prensa, Madrid.
Calatrava-Leyva, J. y Cañero-León, R. (2000). Valoración de fincas olivareras de secano mediante métodos econométricos. Investigación Agraria: Producción y Protección Vegetal, 15 (1-2): 91-103.
Capozza, D. R. y Helsley, R. W. (1989). The fundamentals of land prices and urban growth.
Journal of Urban Economics, 26 (3): 295-306.
García Pérez, J., Cruz Rambaud, S. y Rosado López, Y. (2002). Extensión multi-índice del método beta en valoración agraria. Economía Agraria y Recursos Naturales, 2 (2): 3-26.
García Pérez, J.; Herrerías Pleguezuelo, R. y García García, L.B. (2003). Valoración agraria: contrastes estadísticos para índices y distribuciones en el método de las dos funciones de distribución. Revista Española de Estudios Agrosociales y Pesqueros, 199: 93-118.
Godfrey, L. (1978). Testing for multiplicative heteroscedasticity. Journal of Econometrics, 8: 227-236.
Greene, W.H. (1997). Econometric analysis. Prentice-Hall, New Jersey. Guadalajara, N. (1996). Valoración Agraria. Casos prácticos. Mundi-Prensa, Madrid.
Gujarati, D.; & Porter, D. (2010). Econometría (5 Ed). México: McGraw-Hill Interamericana
McDonald, J. F. y McMillen, D.P. (1998). Land values, land use, and the first Chicago zoning ordinance. Journal of Real Estate Finance and Economics 16 (2): 135-150.
Mendelsohn, R., Nordhaus, W. D. y Shaw, D. (1994). The impact of global warming on agriculture: a Ricardian analysis. American Economic Review 84 (4): 753-771.
Palmquist, R. B. y Danielson, L. E. (1989). A hedonic study of the effects of erosion control and drainage on farmland values. American Journal of Agricultural Economics, 71 (1): 55- 62.
Perry, G.M. y Robison, L.J. (2001). Evaluating the influence of personal relationships on land sale prices: a case study in Oregon. Land Economics, 77 (3): 385-398.
Plantinga, A.J. y Miller, D.J. (2001). Agricultural land values and the value of rights to future land developmen. Land Economics, 77 (1): 56-67.
Roka, F. M. y Palmquist, R. B. (1997). Examining the use of national databases in a hedonic analysis of regional farmland values. American Journal of Agricultural Economics, 79 (5): 1651-1656.
Sandrey R.A., Arthur L.M., Oliveira R.A. y Wilson W.R. (1982). Determinants of Oregon farmland values: A pooled cross-sectorial time series analysis. Western Journal of Agricultural Economics, 7 (2): 211-220.
Segura, B.; García Portillo R. y Vidal F. (1998). Modelos econométricos de valoración: aplicación de la valoración fiscal. Investigación Agraria: Producción y Protección Vegetal, 13 (1-2): 221-241.
Stewart, P.A. y Libby, L. (1998). Determinants of farmland values: The case of DeKalb County,Illynois. Review of Agricultural Economics, 20 (1): 80-95.
White, H. (1980). A heteroscedasticity consistent covariance matrix estimator y a direct test of heteroscedasticity. Econometrica, 48 (4): 817-818.
Wise, J.O. y Dover, H.J. (1974). An evaluation of a statistical method of appraising rural property. The Appraisal Journal, 42 (1): 103-113.