

e- Agronegocios
e-Agronegocios
Revista electrónica publicada por el Centro de Investigación en Economía Agrícola y Desarrollo Agroempresarial, la Escuela de Economía Agrícola y Agronegocios y el Programa de Posgrado en Gerencia Agroempresarial de la Universidad de Costa Rica, 2060, San José, Costa Rica.
![]()
e-Agronegocios
Revista electrónica semestral, ISSN-2215-3462
https://sites.google.com/site/eagronegociosucr/
EFECTO DE LA DISTANCIA A CENTRO URBANO SOBRE EL VALOR DE LAS TIERRAS RURALES: EL CASO DE GUAPILES
Javier Paniagua-Molina
Javier Paniagua-Molina1
Se realizó una investigación para determinar el efecto de la distancia a la ciudad de Guápiles sobre el valor de las tierras rurales periféricas a ella. Se determinó que el valor unitario por cada metro cuadrado decae de forma exponencial conforme aumenta la distancia medida en kilómetros con un coeficiente de regresión de -0,023.
El modelo permitió demostrar que el tamaño de los terrenos y la distancia a centro urbano explicaron el 89% de la variabilidad en el valor unitario de las tierras rurales.
La explosión del desarrollo acelerado de la ciudad de Guápiles ha generado una presión sobre el valor de la tierra, así como expectativas, en ocasiones demasiado elevadas para los propietarios de la tierra.
Fecha de recibido: 10 de setiembre de 2016 Fecha de aprobado: 23 de setiembre de 2016 Fecha de corregido: 30 de setiembre de 2016
![]()
Effect of distance to urban center on the value of rural land: the case of Guapiles
A research was carried out to determine the effect of the distance to the city of Guapiles on the value of the rural lands in the surroundings of this city. It was determined that the unit value per square meter declines exponentially as the distance, measured in kilometers, increases with a regression coefficient of -0.023.
The model showed that land size and distance to urban center accounted for 89% of the variability in the unit value of rural land.
The explosion of the accelerated development of the city of Guápiles has generated a pressure on the value of the land, as well as expectations, sometimes too high for the owners of the land.
El desarrollo acelerado en los últimos años de la ciudad de Guápiles ha generado un incremento en la demanda de la tierra y por ende una presión en el aumento en el precio real de la misma.
El mercado, al estar en alza, genera expectativas en los propietarios de las tierras, y es usual observar como el alza en el precio de oferta es generalizado, cuando este debería ser específico para lotes de uso específico en el desarrollo urbano y comercial de la ciudad.
En la periferia de la ciudad de Guápiles sigue predominando el uso agrícola con actividades como la ganadería, cultivos tropicales y ornamentales. No obstante, existe una presión para sobrevalorar terrenos que no deberían incrementar su valor, al menos como respuesta inmediata al desarrollo mencionado ya que su uso potencial no ha cambiado.
Entidades bancarias han mostrado interés en conocer el valor justo de mercado para terrenos que son segregados de acuerdo a lo que permite la legislación nacional sobre fraccionamiento de parcelas agrícolas con áreas de 5.000 m2, cuyo proceso no representa mayor complejidad en trámites y requisitos, como la que sí presenta un desarrollo de fraccionamiento de áreas menores.
Estos fraccionamientos de parcelas agrícolas han proliferado en los últimos años, en parte, como una forma de vender más fácilmente las tierras en áreas más pequeñas de mejor liquidez que como fincas de mayores extensiones.
Algunas referencias de precios de oferta recientes observados entre 10.000 y 15.000 colones por metro cuadrado para terrenos de 5.000 m² localizados en radio de cerca de 10 km a la redonda de la ciudad de Guápiles genera sospecha de sobrevaloración, de allí la necesidad de contar con un modelo objetivo que permita confirmar si existe o no dicha sobrevaloración.
Esta investigación tiene como objetivo generar un modelo que permita estimar, de forma objetiva, el valor de las tierras en función de su posición con respecto al centro de desarrollo, en este caso, la ciudad de Guápiles.
Este trabajo se desarrolló como parte del proyecto de investigación inscrito ante la Vicerrectoría de Investigación número B5A15 “Valoración de Activos Físicos y Agronegocios en el Medio Rural Costarricense”.
Gurajti y Porter (2010) y Greene (1994) indican que un modelo econométrico es aquel en donde una variable dependiente es explicada por una serie de variables independientes de acuerdo a lo siguiente:
Y 0 1 X1 2 X 2 ... k Xk û
Donde: cada beta corresponde a los coeficientes de regresión para cada una de las variables hasta la k-ésima variable influyente en el modelo y û corresponde a los residuos o errores de cada observación del modelo.
Son numerosos los trabajos que optan por los modelos econométricos para la estimación
del valor de bienes raíces, entre los que se citar los trabajos de Wise y Dover | (1974), |
Sandrey et al. (1982), Capozza y Helsley (1989), Palmquist y Danielson | (1989), |
Mendelsohn et al. (1994), Roka y Palmquist (1997), McDonald y McMillen | (1998), |
Stewart y Libby (1998), Calatrava y Cañero (2000), Plantinga y Millar (2001) y | Perry y |
Robison (2001). |
Entre otras investigaciones se ha demostrado como el valor de la tierra cae entre mayor sea la distancia a un centro de desarrollo (Isakson, 1997; Capozza y Helsley, 1989).
Fraser y Spencer (1998) midieron el efecto de la vista al océano y la proximidad a la playa sobre el valor de la tierra encontrando una gran significancia estadística para los terrenos con vista al mar, en donde también demostraron la relación del valor de la tierra con la distancia, en este caso a la costa.
Muchos autores coinciden en que conforme aumenta el tamaño de la tierra, su valor por metro cuadrado disminuye a tasa decreciente y este mismo patrón aplica para otras variables como la zona (uso), distancia a centros de desarrollo, etc.
El método econométrico, al igual que el método comparativo de mercado, el método multicriterio y otros, forma parte del enfoque de mercado, definido como forma de valuar de acuerdo con las Normas Internacionales de Valuación. Se basa en determinar una curva de mejor ajuste del valor unitario del bien a tasar en función de variables independientes que expliquen ese valor de un bien.
Para que el método econométrico funcione adecuadamente debe cumplirse los supuestos del modelo clásico de regresión lineal normal que implica homogeneidad de varianzas, independencia de las observaciones, no autocorrelación serial en residuos, no sesgo en la especificación del modelo, repeticiones suficientes y que los residuos sigan lo más cercano posible una distribución normal, para lo cual se debe realizar las pruebas estadísticas o contrastes adecuados para cada caso.
Dado que no todos los terrenos tienen una misma área, el tamaño es siempre una variable obligada en cualquier estudio estadístico en el campo de la valoración de tierras.
Cuales otras variables incluir en el modelo dependerán de que tan homogéneas sean las observaciones y de que tanta variabilidad se disponga en los datos.
En el caso bajo estudio, la muestra obtenida de 96 referencias corresponde a observaciones de valores de terrenos muy homogéneos entre sí en cuanto a sus variables de valor presentándose variabilidad en los datos solamente para las variables explicativas seleccionadas para este estudio y manteniendo homogeneidad en otras características.
Para esta investigación, se definieron las siguientes variables:
En la tabla 1 se muestra los resultados del modelo en donde se puede observar como las variables explicativas resultados estadísticamente significativas al 10% de error y 90% de confianza.
Coeficiente | Desv. Típica | Estadístico t | Valor p | ||
const | 13,6327 | 0,334792 | 40,7198 | <0,00001 | *** |
l_T | −0,548423 | 0,0483629 | -11,3397 | <0,00001 | *** |
D | −0,0232238 | 0,012584 | -1,8455 | 0,07520 | * |
Media de la vble. dep. | 9,026331 | D.T. de la vble. dep. | 1,233212 |
Suma de cuad. residuos | 4,774076 | D.T. de la regresión | 0,405738 |
R-cuadrado | 0,898737 | R-cuadrado corregido | 0,891753 |
F(2, 29) | 128,6910 | Valor p (de F) | 3,79e-15 |
Log-verosimilitud | −14,96547 | Criterio de Akaike | 35,93093 |
Criterio de Schwarz | 40,32814 | Crit. de Hannan-Quinn | 37,38848 |
rho | 0,046713 | Durbin-Watson | 1,896656 |
Fuente; elaboración propia
1
0,5
0
-0,5
-1
-1,5
Residuos de la regresión (= l_VU observada - estimada)
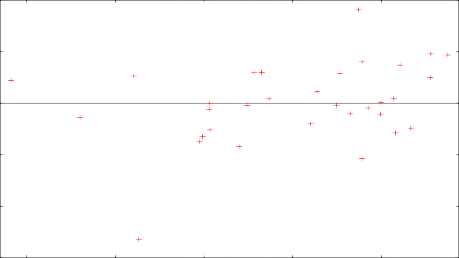
6 7 8 9 10
l_VU
Fuente: elaboración propia
Los residuos siguen no siguen en patrón en específico, y de acuerdo con los contrastes de normalidad, tienden a seguir una distribución normal pero de forma muy ajustada.
El correlagrama de residuos confirma que estos representan “ruido blanco”, lo cual es deseable en el análisis para poder realizar las pruebas de hipótesis sobre significancia de los coeficientes de regresión.
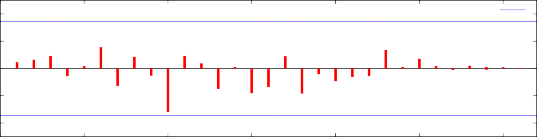
FAC de los residuos
0,4
+- 1,96/T^0,5
0,2
0
-0,2
-0,4
0 5 10 15 20 25 30
retardo
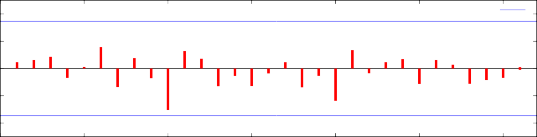
FACP de los residuos
0,4
+- 1,96/T^0,5
0,2
0
-0,2
-0,4
0 5 10 15 20 25 30
retardo
Fuente: elaboración propia
Las probabilidades asociadas a los estadísticos de contrastes de normalidad fueron las siguientes: Doornik-Hansen ( 0,00292603), Shapiro-Wilk (0,0546604), Lilliefors (0,83).
De acuerdo con el test de Durbin Watson no hay presencia de autocorrelación de primer orden y según la prueba de White, no se presentó heterocedasticidad importante ni error de especificación del modelo.
Coeficiente Desv. Típica Estadístico t Valor p
----------------------------------------------------------------
const | −2,00257 | 1,83904 | −1,089 | 0,2862 |
l_T | 0,558381 | 0,477109 | 1,170 | 0,2525 |
D | −0,00712943 | 0,0690849 | −0,1032 | 0,9186 |
sq_l_T | −0,0360173 | 0,0313295 | −1,150 | 0,2608 |
X2_X3 | 0,00227084 | 0,0101134 | 0,2245 | 0,8241 |
sq_D | −2,89426e-05 | 0,00154976 | −0,01868 | 0,9852 |
R-cuadrado | = 0,064148 |
Estadístico de contraste: TR^2 = 2,052736,
con valor p = P(Chi-cuadrado(5) > 2,052736) = 0,841801Chi-cuadrado(5) > 2,052736) = 0,841801
La siguiente figura 3 muestra que el modelo tiene buena capacidad de predicción ya que los valores estimados por este, estuvieron muy cercanos a los observados en la muestra con intervalos de confianza estrechos y estables.
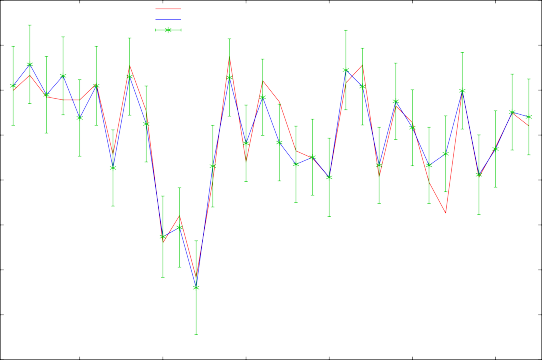
12
l_VU
predicción Intervalo de 95 por ciento
11
10
9
8
7
6
5
4
5 10 15 20 25 30
Fuente: elaboración propia
Const 13,6327 Error medio 0,38
l T -0,548423
D -0,0232238
Area (m²) 5.000,00 Valor mínimo / m² ¢4.585,80
Dist (km) 6,50 Valor máximo / m² ¢9.805,72
Valor medio/m² ¢6.705,75
El modelo de regresión presentó un buen ajuste para las variables explicativas seleccionadas de tamaño y distancia a Guápiles para datos que fueron muy homogéneos en todo lo demás. El modelo explicó 89% de la variabilidad de los datos, quedando el resto 11% por explicar por otras variables que no fueron incluidas en éste.
El lote base a tasar se localiza a 6,5 km de Guápiles y mide 5.000 m², por lo que el modelo pronostica un valor de poco menos de ¢7.000/m², con el intervalo de confianza de la predicción del método econométrico oscila entre ¢4.585,80/m² y ¢9.805,72/m² con un valor medio de ¢6.705,75.
Dado que la expectativa de valor era de cerca de ¢12.000/m², se concluye que efectivamente existe riesgo de sobrevaloración en algunas observaciones de mercado por expectativas de valor altas, lo que justifica la preocupación mostrada por entidades bancarias al respecto y la necesidad de contar con un modelo que estime el valor de forma objetiva.
Alonso, R y Serrano, A. (1998). Valoración Agraria. Casos Prácticos de Valoración
Agraria. Agrícola Española, Madrid.
Alonso, R. e Iruretagoyena, M. T. (1990). Casos prácticos de Valoración Agraria.
Ministerio de
Agricultura Pesca y Alimentación, Madrid.
Arriaza, M.; Cañas Madueño, J.A. y Fernández Sánchez, J.I. (2002). “Valoración de fincas agrarias en la comarca de Pedroches (Córdoba)”. I Congreso Internacional de Valoración y Tasación. Valencia, 3-5 julio.
Bowerman, B.L. y O’Connell, R.T. (1990). Linear statistical models: an applied approach.
Duxbury.
Belmont, CA. Breusch, T. y Pagan, A. (1979). “A simple test for heteroscedasticity and random coefficient variation”. Econometrica, 47: 1287-1294.
Buitrago (2007). Factores determinantes del precio de la tierra rural en los municipios contiguos a Bogotá D.C. Cali, Colombia: Programa Editorial Universidad del Valle.
Caballer, V. (1993). Valoración agraria teoría y práctica. Mundi-Prensa, Madrid. Caballer, V., (1999). Valoración de Árboles. Mundi Prensa, Madrid.
Calatrava Leyva, J. y Cañero León, R. (2000). Valoración de fincas olivareras de secano mediante métodos econométricos. Investig. Agra.: Producción y Protección Vegetal, 15 (1-2): 91-103.
Capozza, D. R. y Helsley, R. W. (1989). The fundamentals of land prices and urban growth. Journal of Urban Economics, 26 (3): 295-306.
Fraser, R. & Spencer, G. (1998) The value of an ocean view: an example of hedonic property amenity valuation. Australian Geographical Studies, 36(1), 94-98.
García Pérez, J., Cruz Rambaud, S. y Rosado López, Y. (2002). Extensión multi-índice del método beta en valoración agraria. Economía Agraria y Recursos Naturales, 2 (2): 3-26.
García Pérez, J.; Herrerías Pleguezuelo, R. y García García, L.B. (2003). Valoración agraria: contrastes estadísticos para índices y distribuciones en el método de las dos funciones de distribución. Revista Española de Estudios Agrosociales y Pesqueros, 199: 93-118.
Godfrey, L. (1978). Testing for multiplicative heteroscedasticity. Journal of Econometrics, 8: 227-236.
Greene, W.H. (1997). Econometric analysis. Prentice-Hall, New Jersey.
Gujarati, D.; & Porter, D. (2010). Econometría (5 Ed). México: McGraw-Hill Interamericana
Isackson, W. (1997). An empirical analysis of the determinants of the value of vacant land.
Journal of Real Estate Research 13 (2), 103-114.
McDonald, J. F. y McMillen, D.P. (1998). Land values, land use, and the first Chicago zoning ordinance. Journal of Real Estate Finance and Economics 16 (2): 135-150.
Mendelsohn, R., Nordhaus, W. D. y Shaw, D. (1994). The impact of global warming on agriculture: a Ricardian analysis. American Economic Review 84 (4): 753-771.
Palmquist, R. B. y Danielson, L. E. (1989). A hedonic study of the effects of erosion control and drainage on farmland values. American Journal of Agricultural Economics, 71 (1): 55-62.
Perry, G.M. y Robison, L.J. (2001). Evaluating the influence of personal relationships on land sale prices: a case study in Oregon. Land Economics, 77 (3): 385-398.
Plantinga, A.J. y Miller, D.J. (2001). Agricultural land values and the value of rights to future land development. Land Economics, 77 (1): 56-67.
Roka, F. M. y Palmquist, R. B. (1997). Examining the use of national databases in a hedonic analysis of regional farmland values. American Journal of Agricultural Economics, 79 (5): 1651-1656.
Sandrey R.A., Arthur L.M., Oliveira R.A. y Wilson W.R. (1982). Determinants of Oregon farmland values: A pooled cross-sectorial time series analysis. Western Journal of Agricultural
Economics, 7 (2): 211-220.
Segura, B.; García Portillo R. y Vidal F. (1998). Modelos econométricos de valoración: aplicación de la valoración fiscal. Investigación Agraria: Producción y Protección Vegetal, 13 (1-2): 221-241.
Stewart, P.A. y Libby, L. (1998). Determinants of farmland values: The case of DeKalb County,Illynois. Review of Agricultural Economics, 20 (1): 80-95.
White, H. (1980). A heteroscedasticity consistent covariance matrix estimator y a direct test ofheteroscedasticity. Econometrica, 48 (4): 817-818.
Wise, J.O. y Dover, H.J. (1974). An evaluation of a statistical method of appraising rural property. The Appraisal Journal, 42 (1): 103-113.