e- Agronegocios

e-Agronegocios

Revista electrónica publicada por el Centro de Investigación en Economía Agrícola y Desarrollo Agroempresarial, la Escuela de Economía Agrícola y Agronegocios y el Programa de Posgrado en Gerencia Agroempresarial de la Universidad de Costa Rica, 2060, San José, Costa Rica.

e-Agronegocios

Revista electrónica semestral, ISSN-2215-3462

Volumen 3, número 1, articulo 1

Enero-junio 2017

Publicado 1 de enero, 2017

https://sites.google.com/site/eagronegociosucr/

ANALISIS DE RIESGO BAJO SIMULACION MONTECARLO PARA UN PROYECTO DE INDUSTRIALIZACION DE CARNE DE BOVINO

Javier Paniagua-Molina

Análisis de riesgo bajo simulación Monte Carlo para un proyecto de industrialización de carne de bovino

Javier Paniagua-Molina1

RESUMEN

Se realizó un análisis de riesgo mediante simulación Monte Carlo para un proyecto de establecimiento de planta de sacrificio de bovinos y porcinos en la Zona Norte de Costa Rica. Las variables de riesgo más sensibles fueron los precios de los boletos de sacrificio y la capacidad de uso de la planta para los primeros 4 años de operación.

Las variables de respuesta del modelo de simulación fueron el VAN y la TIR y ambas en escenarios dinámicos de 1000 corridas de simulación resultaron muy similares a las obtenidas en el escenario estático. El coeficiente de variación para el VAN fue de 24,63% y para la TIR de 9,02%, asimismo en ninguno de los casos se obtuvo ninguna probabilidad de retorno negativo. Las medidas de riesgo anteriores sugieren que el proyecto presenta un riesgo medio representado por la variabilidad importante en los flujos, más sin probabilidad de obtener retorno negativo.

Palabras clave: Análisis de riesgo, simulación Monte Carlo, industria de carne

Fecha de recibido: 8 de agosto de 2016 Fecha de aprobado: 22 agosto de 2016 Fecha de corregido: 30 de agosto de 2016

1 Economista Agrícola, Master en Administración y Dirección de Empresas con Énfasis en Finanzas, docente Escuela de Economía Agrícola y Agronegocios, investigador en el Centro de Investigación en Economía Agrícola y Desarrollo Agroempresarial (CIEDA), Universidad de Costa Rica, javier.paniagua@ucr.ac.cr

Risk analysis under Monte Carlo simulation for a beef industrialization project

ABSTRACT

A risk analysis was carried out using Monte Carlo simulation for a project to establish a slaughtering plant for cattle and pigs in the Northern Zone of Costa Rica. The most sensitive risk variables were the prices of the slaughter tickets and the capacity of the plant for the first 4 years of operation.

The response variables of the simulation model were the NPV and the TIR and both in dynamic scenarios of 1000 simulation runs were very similar to those obtained in the static scenario. The coefficient of variation for the NPV was 24.63% and for the IRR of 9.02%, likewise in no case was there any negative probability of return. The previous risk measures suggest that the project presents an average risk represented by the significant variability in flows, but with no probability of obtaining a negative return.

Key words: Risk analysis, Monte Carlo simulation, meat industry

INTRODUCCION

Ante la solicitud de una organización, el Centro de Investigación en Economía Agrícola y Desarrollo Agroempresarial de la Universidad de Costa Rica, procedió a realizar el estudio denominado de factibilidad para la instalación de una de una planta de sacrificio de ganado bovino y porcino para la en la Región Norte del País.

Como parte de ese estudio se procedió a incorporar un análisis de riesgo bajo simulación Monte Carlo procedió a solicitar la incorporación de un análisis de riesgo cuantitativo mediante las técnicas de simulación de Monte Carlo, con la finalidad de conocer el riesgo asociado con factores externos a la planta procesadora.

El análisis de riesgo cuantitativo involucra el uso de la simulación de Monte Carlo, llamado también método de ensayos estadísticos, que consiste en una técnica de simulación de situaciones inciertas que permite definir valores esperados para variables no controlables, mediante la selección aleatoria de valores probables, donde la probabilidad de elegir entre todos los resultados posibles, está en relación directa con sus respectivas distribuciones de probabilidad (Savvides, 1994). Aplicado a la evaluación de proyectos, el análisis de riesgo permite obtener un valor esperado o probabilístico del VAN, muy superior al VAN obtenido en el escenario estático ya que incorpora la variabilidad esperada en las variables que constituyen el modelo económico parametrizado en hojas electrónicas, por ejemplo.

Este trabajo se desarrolló como parte del proyecto de investigación inscrito ante la Vicerrectoría de Investigación número B5A12 “Modelación Econométrica de Mercados

Agrícolas y Aplicación de Métodos Cuantitativos para Optimización de Procesos en Agronegocios”.
REFERENTE TEORICO

En un sentido amplio, el riesgo se asocia como la representación de cualquier situación en donde los eventos no se conocen con certeza (Chavas, 2004), no obstante es importe reconocer la diferencia que existe entre riesgo e incertidumbre.

Riesgo se define como aquella variabilidad esperada de los eventos en los cuales es posible medir su probabilidad de ocurrencia, mientras que incertidumbre corresponde a la variabilidad de eventos en los que no es posible, o es difícil, estimar las probabilidades de ocurrencia (Chavas, 2004).

(Sapag & Sapag, 2008) indican que el modelo de Monte Carlo, llamado también método de ensayos estadísticos, es una técnica de simulación de situaciones inciertas que permite definir valores esperados para variables no controlables, mediante la selección aleatoria de valores probables, donde la probabilidad de elegir entre todos los resultados posibles, está en relación directa con sus respectivas distribuciones de densidad de probabilidad.

Una distribución de densidad de probabilidad, es una función generalizada que asigna probabilidades a todos los posibles resultados de un experimento aleatorio, normalmente se denomina como función de densidad de probabilidad y se abrevia como PDF por sus siglas en inglés (probability density funtion (Jackel, 2002)

Según Jackel (2002), la relación entre la probabilidad de que un valor X de un experimento aleatorio sea un elemento de un conjunto de valores S y una densidad de probabilidad de un experimento aleatorio, se define como:
Px  S    x
S
El mismo autor define el valor esperado para una cantidad sujeta a incertidumbre, como la probabilidad promedio ponderada y se define así:

E  f  
 fdx

Como la densidad de probabilidad depende de la variable x, la cual tiene un comportamiento aleatorio con una probabilidad asociada, entonces la ecuación anterior se puede expresar como:
Ex  f x 

 f xxdx


El uso más común para las simulaciones de Monte Carlo en finanzas es cuando se necesita calcular un valor esperado para una función f(x) dada una densidad de probabilidad x sobre la variable x perteneciente al conjunto de los números reales y a cualquier espacio
vectorial “n”, Rn.
v  E x  f x  f xxdx
n

El análisis de riesgo en la evaluación de proyectos con la ayuda de la técnica de simulación probabilística basada en el método de Monte Carlo, es una metodología, por medio de la cual, un modelo matemático parametrizado está sujeto a un número determinado de corridas de simulación usando como variable rspuesta usualmente el Valor Actual Neto del proyecto (VAN) (Savvides, 1994).

Durante el proceso de simulación, sucesivos escenarios son construidos utilizando valores para las variables claves de riesgo, éstos son asignados por el sistema con base en las distribuciones de probabilidad determinadas para cada variable. Determinar cual es la distribución de probabilidad adecuada para cada variable depende de estudios previos del fenómeno, debido a que se necesitan series históricas de datos para poder ajustarla.

El primer paso en la aplicación del análisis de riesgo es la construcción de un modelo parametrizado de proyección, el cual sea capaz de predecir correctamente el resultado sobre una o más variables respuesta, de los cambios en los valores de las variables explicativas del modelo. Se requiere el establecimiento de relaciones matemáticas entre las variables explicativas y la variable respuesta, por ejemplo, que las ventas sean producto de la multiplicación del precio de venta por la cantidad vendida, que los costos totales sean producto de la multiplicación del costo unitario por la cantidad de insumos requerida (Savvides, 1994).

Para efectos prácticos, la creación del modelo de proyección se debe realizar con ayuda de un programa de cómputo como una hoja electrónica de cálculo para facilitar el procesamiento rápido de los datos, como puede ser el @RISK de la empresa Palisade (Wayne, 2001), no obstante existen otras herramientas de software en el mercado como el Crystal Ball®, Riskease® y Riskmaster® entre otros.

Finalmente, para el pronóstico de las variables macroeconómicas se empleó modelos de tipo ARIMA con la siguiente estructura:

(B)Zt    (B)at
Z es la variable de interés y a esa variable se le puede multiplicar un polinomio que es un phi de B, una progresión de orden p. El polinomio B es un cita de orden q que multiplica a at. B viene de “back shift” que rezaga, también conocido como operador L (lag)

(B)  (1 1B  2
B2 ...  
Bp )
(B)  (1 1B  2
B2 ...  
Bq )

p
q
METODOLOGIA
1. Datos
  
  Los datos fueron recopilados del propio estudio de factibilidad realizado en cuento al proceso industrial se refiere, considerando como válidos los modelos organizacional y técnico para el desarrollo de los procesos del proyecto.
  
  Por otra parte, fue necesario obtener datos que colecta el Consejo Nacional de Producción (CNP) partiendo del supuesto que la estacionalidad en el mercado de canales tiene un efecto que se trasmite a los precios de los boletos de los animales a sacrificar. Si hay exceso de oferta de animales, el precio que se liquida al productor cae, mientras que si hay escases, es de esperar que el precio suba.
  
  El proyecto consiste en una planta industrializadora que ofrece los servicios de sacrificio de animales tanto bovinos como porcinos por medio de boleto respectivo. Las capacidades de uso de la planta para los primeros 4 años de operación de proyecto, así como la variabilidad de los gastos desembolsables (VGD) y la variabilidad de la inversión física (VINF), se estimaron con base en criterio de experto de los usuarios y de los resultados del estudio de ingeniería.
  
  2.3 Modelado
  
  Como variables macroeconómicas importantes a considerar en este proyecto están la tasa de interés y la tasa de inflación local, y como no se encontró proyecciones en el estudio de factibilidad, se procedió a la aplicación de modelos de series de tiempo tipo ARIMA (Autoregressive Integrated Moving Average) para la proyección futura de dichas variables.
  
  Se realizó 1000 corridas de simulación multiescenario en donde el programa de cómputo Risk Master generó múltiples combinaciones de posiciones de las variables de riesgo de acuerdo a sus respectivas distribuciones de probabilidad.

RESULTADOS Y DISCUSION

Modelación

En la tabla 1 se presenta los parámetros del modelo definidos como índices técnicos y de mercado que se tienen un comportamiento estático o dinámico, en cuyo caso está asociada una distribución de probabilidad. Por su parte, la tabla 2 presenta una proyección de la producción y las ventas de acuerdo a las estimaciones realizadas para el proyecto en el estudio de mercado correspondiente y finalmente la tabla 3 muestra el flujo de efectivo para el proyecto en el escenario estático.

Tabla 1. Tabla de parámetros del modelo

TABLA DE PARAMETROS								CALCULOS INTERMEDIOS
Cuero/ Res	80,00%	<<		Sangre de cerdo (kg)/animal	3	<<		Harina de cerdo/animal:	0,3249
Sebo de cerdo/animal:	8	<<		Sangre de res (kg)/animal	12	<<		Harina de res/animal:	1,2996
Sebo de res/animal:	30	<<		Harina de cerdo/Sangre de cerdo:	10,83%	<<
Rendimiento sebo en cerdo:	40,00%	<<		Harina de res/Sangre de res:	10,83%	<<
Rendimiento sebo en res:	40,00%	<<		Capacidad máxima en cerdos:	8152
				Capacidad máxima en reses:	3135
Tasa de impuesto de la renta	0%
Precio inicial Boleto de cerdos (¢/ud)	¢5.900,00			Expectativas de tasas de interés:	1,25
Precio inicial Boleto de res (¢/und)	¢20.500,00			Beta de la actividad:	0,8
Precio inicial Cuero (¢/unid)	¢3.500,00			Rendimiento esperado del mercado nominal	25,00%
Precio inicial Harina de sangre (¢/kg)	¢103,00			Días de capital de trabajo	90
Precio inicial Grasa (¢/kg)	¢325,00			Variabilidad de gastos desembolsables	1	<<
Precio inicial Otros (¢/kg)	¢300,00			Variabilidad de inversión física	1	<<
			Año 0	Año 1 Año 2 Año 3	Año 4		Año 5	Año 6 Año 7	Año 8	Año 9	Año 10
	2011		2012	2013 2014 2015	2016		2017	2018 2019	2020	2021	2022
Indice de precios al consumidor (IPC)	1,4683		1,57627	1,68441 1,7885 1,9085	2,0319		2,14977	2,27679 2,4109	2,54201	2,67778	2,82135
Tasa de inflación anual			7,35%	6,86% 6,18% 6,71%	6,47%		5,80%	5,91% 5,89%	5,44%	5,34%	5,36%
Indice de inflación del proyecto			1,00	1,07 1,13 1,21	1,29		1,36	1,44 1,53	1,61	1,70	1,79
Tasa de interés anual (TBP)			8,40%	8,30% 7,43% 7,25%	7,42%		7,14%	6,75% 6,64%	6,55%	6,32%	6,09%
Tasa de interés anual (TBP) revisada por	expectativas		10,50%	10,37% 9,28% 9,07%	9,27%		8,92%	8,43% 8,29%	8,19%	7,89%	7,62%
Capacidad de planta utilizada (%):				70,0% 75,0% 80,0%	85,0%		90,0%	90,0% 90,0%	90,0%	90,0%	90,0%
Fuente: elaboración propia

Tabla 2. Plan de producción y ventas

		Año 0	Año 1	Año 2	Año 3	Año 4	Año 5	Año 6	Año 7	Año 8	Año 9	Año 10
	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020	2021	2022
Boleto de cerdos (unidades)			5706,40	6114,00	6521,60	6929,20	7336,80	7336,80	7336,80	7336,80	7336,80	7336,80
Boleto de res (unidades)			2194,50	2351,25	2508,00	2664,75	2821,50	2821,50	2821,50	2821,50	2821,50	2821,50
Cuero			1755,60	1881,00	2006,40	2131,80	2257,20	2257,20	2257,20	2257,20	2257,20	2257,20
Harina de sangre (kg)			4705,98	5042,12	5378,26	5714,41	6050,55	6050,55	6050,55	6050,55	6050,55	6050,55
Grasa (kg)			44594,48	47779,80	50965,12	54150,44	57335,76	57335,76	57335,76	57335,76	57335,76	57335,76
Otros (kg)			22297,24	23889,9	25482,56	27075,22	28667,88	28667,88	28667,88	28667,88	28667,88	28667,88
Precio Boleto de cerdos (¢/ud)			¢6.304,77	¢6.694,38	¢7.143,54	¢7.605,43	¢8.046,62	¢8.522,06	¢9.024,03	¢9.514,78	¢10.022,97	¢10.560,35
Precio Boleto de res (¢/und)			¢21.906,40	¢23.260,13	¢24.820,78	¢26.425,64	¢27.958,59	¢29.610,53	¢31.354,69	¢33.059,82	¢34.825,56	¢36.692,75
Precio Cuero (¢/unid)			¢3.740,12	¢3.971,24	¢4.237,69	¢4.511,70	¢4.773,42	¢5.055,46	¢5.353,24	¢5.644,36	¢5.945,83	¢6.264,62
Percio Harina de sangre (¢/kg)			¢110,07	¢116,87	¢124,71	¢132,77	¢140,47	¢148,77	¢157,54	¢166,11	¢174,98	¢184,36
Precio Grasa (¢/kg)			¢347,30	¢368,76	¢393,50	¢418,94	¢443,25	¢469,44	¢497,09	¢524,12	¢552,11	¢581,71
Precio Otros (¢/kg)			¢320,58	¢340,39	¢363,23	¢386,72	¢409,15	¢433,32	¢458,85	¢483,80	¢509,64	¢536,97
Fuente: elaboración propia

e-Agronegocios • Volumen 3, número 1, artículo 1, ene – jun, 2017

Tabla 3. Flujo de efectivo del proyecto

	Año 0	Año 1	Año 2	Año 3	Año 4	Año 5	Año 6	Año 7	Año 8
	2012	2013	2014	2015	2016	2017	2018	2019	2020
Ingresos Boleto de cerdos		431.730.439	491.153.255	559.047.835	632.394.486	708.437.148	750.295.434	794.490.164	837.696.272
Boleto de res 576.883.202 656.284.655 747.006.178 845.012.821 946.621.905 1.002.553.429 1.061.606.939 1.119.339.440 1
Cuero	78.793.803		89.638.880	102.030.112	115.416.385	129.294.699	136.934.127	144.999.972	152.885.387
Harina de sangre	6.215.641		7.071.153	8.048.634	9.104.609	10.199.398	10.802.034	11.438.307	12.060.347
Grasa	185.850.148		211.430.321	240.657.396	272.231.463	304.966.102	322.985.143	342.009.971	360.609.219
Otros	85.776.992		97.583.225	111.072.644	125.645.291	140.753.585	149.070.066	157.850.756	166.435.024
Total Ingresos	1.365.250.225		1.553.161.489	1.767.862.799	1.999.805.055	2.240.272.838	2.372.640.233	2.512.396.109	2.649.025.689 2
Gastos desembolsables Gastos administrativos		317.342.745	336.953.295	359.561.287	382.809.840 405.016.541		428.947.102 454.213.418 478.914.534
Gastos operativos		127.181.896	135.041.244	144.101.881	153.419.236 162.319.047		171.909.731 182.035.748 191.935.249
Mantenimiento		53.296.218	56.589.717	60.386.623	64.291.108 68.020.619		72.039.644 76.283.002 80.431.438
Otros gastos		6.579.083	6.985.645	7.454.349	7.936.333 8.396.717		8.892.841 9.416.657 9.928.755
Costo por imprevistos		25.219.997	26.778.495	28.575.207	30.422.826 32.187.646		34.089.466 36.097.441 38.060.499
Total gastos desembolsables		529.619.939	562.348.395	600.079.347	638.879.343 675.940.570		715.878.783 758.046.266 799.270.475
Gastos no desembolsables		0
Depreciación equipo e infraestrutura		166.248.577	166.248.577	166.248.577	166.248.577 166.248.577		166.248.577 166.248.577 166.248.577
Amortización activo nominal		13.714.901	13.714.901	13.714.901	13.714.901 13.714.901		0 0 0
Total gastos no desembolsables		179.963.478	179.963.478	179.963.478	179.963.478 179.963.478		166.248.577 166.248.577 166.248.577

Gastos de operación		709.583.417	742.311.873	780.042.825	818.842.821 855.904.048		882.127.359 924.294.842 965.519.052 1

Utilidad de operación		655.666.809	810.849.616	987.819.974	1.180.962.234 1.384.368.789		1.490.512.874 1.588.101.267 1.683.506.638 1
Impuesto de la renta 0%		0	0	0	0 0		0 0 0
Utilidad neta		655.666.809	810.849.616	987.819.974	1.180.962.234 1.384.368.789		1.490.512.874 1.588.101.267 1.683.506.638 1
Gastos no desembolsables		179.963.478	179.963.478	179.963.478	179.963.478 179.963.478		166.248.577 166.248.577 166.248.577
Inversiones físicas	3.076.915.146
Inversión en capital de trabajo Recuperación de capital Valor de rescate del proyecto	130.591.218
Flujo de operación	-3.207.506.364	835.630.286	990.813.094	1.167.783.452	1.360.925.712 1.564.332.267		1.656.761.450 1.754.349.843 1.849.755.214 1

Tasa libre de riesgo esperada nominal	8,90% <<		VAN básico				1.945.303.680
Beta	0,8
Rendimiento esperado del mercado nominal	25,00%		Tasa interna de	retorno (TIR)			35,81%

Costo de capital de los recursos propios nominal (Ks) 21,78%

ISSN 2215-3462 8

Análisis de sensibilidad y riesgo

Figura 1. Análisis de sensibilidad para las variables del proyecto

Carnicoop (Risk Master) Sensitivity of VAN básico

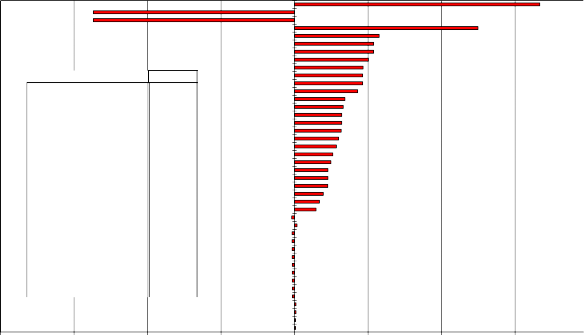
Precio Boleto Res Precio Boleto Cerdo

Precio Grasa

Sebo/res

Variabilidad de GDB Variabilidad de INVF

VAN básico

Capacidad 2013

Capacidad 2014 Precio Grasa Capacidad 2015

Capacidad 2016 Sebo/res

Precio Boleto Cerdo

Precio Boleto

IPC 2014

Rend sebo en cerdo

IPC 2013

Precio Cuero IPC 2020

TBP 2013

TBP 2016

TBP 2018

TBP 2021

Rend sangre res

RV22 Precio Boleto Res 1,67

RV27 Variabilidad de GDB -1,37

RV28 Variabilidad de INVF -1,37

RV21 Precio Boleto Cerdo 1,25

RV38 Capacidad 2013 0,58

RV39 Capacidad 2014 0,54

RV25 Precio Grasa 0,54

RV40 Capacidad 2015 0,50

RV41 Capacidad 2016 0,47

RV31 Sebo/res 0,46

RV33 Rend sebo en res 0,46

RV42 Capacidad 2017 0,43

RV2 IPC 2014 0,34

RV3 IPC 2015 0,33

RV30 Sebo/cerdo 0,32

RV32 Rend sebo en cerdo 0,32

RV4 IPC 2016 0,32

RV5 IPC 2017 0,30

RV1 IPC 2013 0,29

RV6 IPC 2018 0,26

RV26 Precio Otros 0,25

RV23 Precio Cuero 0,23

RV29 Cuero/res 0,23

TBP 2013

TBP 2014

TBP 2016

TBP 2015

TBP 2017

TBP 2018

TBP 2019

TBP 2020

TBP 2021

TBP 2022

Rend sebo en res Capacidad 2017

IPC 2014

IPC 2015

Sebo/cerdo

Rend sebo en cerdo IPC 2016

IPC 2017

IPC 2013

IPC 2018

Precio Otros Precio Cuero Cuero/res IPC 2019

IPC 2020

IPC 2021

IPC 2022

Precio Harina sangre

Sangre por res Rend sangre res Sangre por cerdo Rend sangre cerdo

-2 -1,5 -1 -0,5 0 0,5 1 1,5

sensitivity index

Fuente: Elaboración propia

La figura anterior permite observar como las variables más sensibles ante las cuales se afecta el VAN, son los precios de los productos, la variabilidad de los gastos desembolsables, la variabilidad en el monto de la inversión física y la capacidad de planta definidas para los primeros 4 años.

Las dos tablas siguientes muestras estimaciones para la tasa básica pasiva y el índice de precios al consumidor generados por medio de modelos de series de tiempo tipo ARIMA.

Tabla 4. ARIMA, usando las observaciones 1982-2011 (T = 30)

Variable dependiente: (1-L)^2 Nivel_de_precio Desviaciones típicas basadas en el Hessiano

	Coeficiente	Desv. Típica	z	Valor p
const	0,00350169	0,000477897	7,3273	<0,00001	***
phi_1	-0,310169	0,256647	-1,2085	0,22684
phi_2	-0,593808	0,183328	-3,2390	0,00120	***
phi_3	0,224411	0,320157	0,7009	0,48334
theta_1	-0,0330324	0,197044	-0,1676	0,86687
theta_2	0,0330324	0,19603	0,1685	0,86618
theta_3	-1	0,168869	-5,9218	<0,00001	***

Media de la vble. dep.	0,002125	D.T. de la vble. dep.	0,017166
media innovaciones	-0,001278	D.T. innovaciones	0,012893
Log-verosimilitud	84,89793	Criterio de Akaike	-153,7959
Criterio de Schwarz	-142,5863	Crit. de Hannan-Quinn	-150,2098

Fuente: elaboración propia

Tabla 5. ARIMA, usando las observaciones 1981-2011 (T = 31) Variable dependiente: (1-L) l_Tasa_de_interés (TBP)

	Coeficiente	Desv. Típica	z	Valor p
const	-0,0277437	0,0211547	-1,3115	0,18970
phi_1	-0,164715	0,330737	-0,4980	0,61847
phi_2	-0,607467	0,27689	-2,1939	0,02824	**
theta_1	-0,045116	0,387399	-0,1165	0,90729
theta_2	0,208525	0,351805	0,5927	0,55336

Media de la vble. dep.	-0,028448	D.T. de la vble. dep.	0,205775
media innovaciones	-0,003378	D.T. innovaciones	0,176741
Log-verosimilitud	9,478212	Criterio de Akaike	-6,956425
Criterio de Schwarz	1,647498	Crit. de Hannan-Quinn	-4,151760

Fuente: elaboración propia

Tabla 6. Pronóstico del Indice de Precios al Consumidor como predictor de la tasa de inflación local. Intervalos de confianza al 95%

Obs predicción Desv. Típica Intervalo de 95% Error

estándar

IPC Min IPC Medio IPC Máx Tasa Inflación

media

2012 1,57627 0,0128934 (1,55100, 1,60154) 0,025271 1,5510 1,5763 1,6015 7,35%

2013 1,68441 0,0249513 (1,63551, 1,73332) 0,048904 1,6355 1,6844 1,7333 6,86%

2014 1,7885 0,0346012 (1,72068, 1,85632) 0,067817 1,7207 1,7885 1,8563 6,18%

2015 1,9085 0,0404895 (1,82914, 1,98786) 0,079358 1,8291 1,9085 1,9879 6,71%

2016 2,0319 0,0462201 (1,94131, 2,12249) 0,090590 1,9413 2,0319 2,1225 6,47%

2017 2,14977 0,0521879 (2,04748, 2,25206) 0,102286 2,0475 2,1498 2,2521 5,80%

2018 2,27679 0,0567212 (2,16562, 2,38796) 0,111172 2,1656 2,2768 2,3880 5,91%

2019 2,4109 0,0608291 (2,29167, 2,53012) 0,119223 2,2917 2,4109 2,5301 5,89%

2020 2,54201 0,0652767 (2,41407, 2,66995) 0,127940 2,4141 2,5420 2,6699 5,44%

2021 2,67778 0,0691593 (2,54223, 2,81333) 0,135550 2,5422 2,6778 2,8133 5,34%

2022 2,82135 0,0725853 (2,67909, 2,96362) 0,142265 2,6791 2,8214 2,9636 5,36%

2023 2,96495 0,0761929 (2,81562, 3,11429) 0,149335 2,8156 2,9650 3,1143 5,09%

Fuente: elaboración propia

Tabla 7. Pronóstico de la tasa de interés (Tasa Básica Pasiva). Intervalos de confianza al 95%

Obs predicción Desv. Típica Intervalo de 95% Error

estándar

TBP Min TBP

Media

TBP Máxima

2012 2,12859 0,176741 (1,78219, 2,47500) 2,34% 8,16% 10,50% 12,84%

2013 2,11596 0,225258 (1,67447, 2,55746) 2,46% 7,92% 10,37% 12,83%

2014 2,00486 0,237496 (1,53937, 2,47034) 2,49% 6,80% 9,28% 11,77%

2015 1,98166 0,261061 (1,46999, 2,49333) 2,54% 6,52% 9,07% 11,61%

2016 2,00381 0,297207 (1,42129, 2,58633) 2,64% 6,63% 9,27% 11,91%

2017 1,96509 0,319181 (1,33950, 2,59067) 2,70% 6,22% 8,92% 11,62%

2018 1,90884 0,334527 (1,25318, 2,56450) 2,74% 5,69% 8,43% 11,17%

2019 1,89246 0,354871 (1,19693, 2,58800) 2,79% 5,50% 8,29% 11,09%

2020 1,88016 0,376333 (1,14256, 2,61776) 2,86% 5,34% 8,19% 11,05%

2021 1,84297 0,392946 (1,07281, 2,61313) 2,90% 4,99% 7,89% 10,80%

2022 1,8074 0,408296 (1,00716, 2,60765) 2,95% 4,67% 7,62% 10,57%

2023 1,78669 0,425196 (0,953318, 2,62005) 3,00% 4,46% 7,46% 10,46%

Fuente: elaboración propia

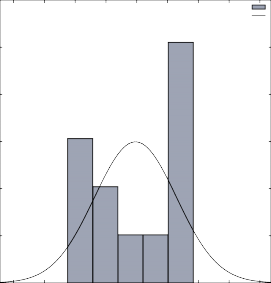
Las figuras siguientes muestran las distribuciones de probabilidad para el precio en canal de la carne de res y de cerdo, en donde se observa que en ambos casos presentan una marcada estacionalidad durante el año. Cabe agregar que los contrastes de normalidad no dieron resultados satisfactorios, por lo que se considera mejor emplear distribuciones tipo STEP (usando el histograma) para la simulación de riesgo.

Figura 2. Distribución de probabilidad para el precio local de la carne de res

Estadístico para el contraste de normalidad: Chi-cuadrado(2) = 7,593 [0,0224]

I_Bov N(0,99799 0,066655)

Distribución de frecuencias para I_Bov, observaciones 1-12 número de cajas = 5, media = 0,997995, desv.típ.=0,0666553

intervalo punto medio frecuencia rel acum.

< 0,92859	0,90819	3	25,00%	25,00% *********
0,92859 - 0,96941	0,94900	2	16,67%	41,67% ******
0,96941 - 1,0102	0,98982	1	8,33%	50,00% ***
1,0102 - 1,0510	1,0306	1	8,33%	58,33% ***
>= 1,0510	1,0714	5	41,67%	100,00% **************

D e n s id a d

Contraste de Doornik-Hansen = 7,59345, con valor p 0,0224442 W de Shapiro-Wilk = 0,836143, con valor p 0,024862

2 Contraste de Lilliefors = 0,262403, con valor p ~= 0,02

Contraste de Jarque-Bera = 1,53343, con valor p 0,464538

0,8 0,85 0,9 0,95 1 1,05 1,1 1,15 1,2

I_Bov

Fuente: elaboración propia

Figura 3. Distribución de probabilidad el precio local de la carne de cerdo

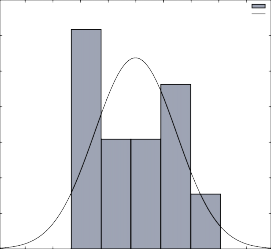
3,5

2,5

D ensidad

1,5

0,5

Estadístico para el contraste de normalidad: Chi-cuadrado(2) = 1,163 [0,5590]

I_Cerd N(0,99873 0,14841)

Distribución de frecuencias para I_Cerd, observaciones 1-12 número de cajas = 5, media = 0,998733, desv.típ.=0,148406

intervalo punto medio frecuencia rel acum.

< 0,87419 0,82019 4 33,33% 33,33% ************

0,87419 - 0,98220 0,92820 2 16,67% 50,00% ******

0,98220 - 1,0902 1,0362 2 16,67% 66,67% ******

1,0902 - 1,1982 1,1442 3 25,00% 91,67% *********

>= 1,1982 1,2522 1 8,33% 100,00% ***

Contraste de normalidad de I_Cerd:

Contraste de Doornik-Hansen = 1,16335, con valor p 0,558963 W de Shapiro-Wilk = 0,910665, con valor p 0,217577 Contraste de Lilliefors = 0,174202, con valor p ~= 0,39 Contraste de Jarque-Bera = 0,889906, con valor p 0,640854

0,6 0,7 0,8 0,9 1 1,1 1,2 1,3 1,4

I_Cerd

Fuente: elaboración propia

Tabla 8. Tabla de variables de riesgo

No.

Risk variable

Base

value

Prob.

distr.

Range

Skew

ness

Truncation

Correlations

Description

MIN

MAX

MIN

MAX

Ind.Var

r [-1..1]

Carnicoop (Risk Master)



1 IPC 2013	1,68441	NORM	1,6355	1,73333
2 IPC 2014	1,7885	NORM	1,7207	1,8563
3 IPC 2015	1,9085	NORM	1,8291	1,9879
4 IPC 2016	2,0319	NORM	1,9413	2,1255
5 IPC 2017	2,14977	NORM	2,0475	2,2521
6 IPC 2018	2,27679	NORM	2,1656	2,388
7 IPC 2019	2,4109	NORM	2,2917	2,5301
8 IPC 2020	2,54201	NORM	2,4141	2,6699
9 IPC 2021	2,67778	NORM	2,5422	2,8133
10 IPC 2022	2,82135	NORM	2,6791	2,9636
11 TBP 2013	8,30%	NORM	5,84%	10,75%
12 TBP 2014	7,43%	NORM	4,94%	9,91%
13 TBP 2015	7,25%	NORM	4,71%	9,80%
14 TBP 2016	7,42%	NORM	4,78%	10,06%
15 TBP 2017	7,14%	NORM	4,44%	9,83%
16 TBP 2018	6,75%	NORM	4,01%	9,48%
17 TBP 2019	6,64%	NORM	3,84%	9,43%
18 TBP 2020	6,55%	NORM	3,70%	9,41%
19 TBP 2021	6,32%	NORM	3,41%	9,22%
20 TBP 2022	6,09%	NORM	3,15%	9,04%
21 Precio Boleto Cerdo	¢5.900,00	STEP	¢4.838,59	¢7.387,98
22 Precio Boleto Res	¢20.500,00	STEP	¢18.616,05	¢21.963,70
23 Precio Cuero	¢3.500,00	NORM	¢2.000,00	¢5.000,00	0%
24 Precio Harina sangre	¢103,00	NORM	¢73,00	¢133,00	0%
25 Precio Grasa	¢325,00	NORM	¢250,00	¢400,00	0%
26 Precio Otros	¢300,00	NORM	¢270,00	¢330,00	0%
27 Variabilidad de GDB	1	NORM	0,85	1,15
28 Variabilidad de INVF	1	NORM	0,85	1,15
29 Cuero/res	80,00%	NORM	74,00%	86,00%	0%
30 Sebo/cerdo	8	NORM	5	11	0%
31 Sebo/res	30	NORM	18	42	0%
32 Rend sebo en cerdo	40,00%	NORM	25,00%	55,00%	0%
33 Rend sebo en res	40,00%	NORM	25,00%	55,00%	0%
34 Sangre por cerdo	3	NORM	2,25	3,75	0%
35 Sangre por res	12	NORM	9	15	0%
36 Rend sangre cerdo	10,83%	NORM	7,83%	13,83%	0%
37 Rend sangre res	10,83%	NORM	7,83%	13,83%	0%
38 Capacidad 2013	70,0%	NORM	67,0%	73,0%	0%
39 Capacidad 2014	75,0%	NORM	72,0%	78,0%	0%
40 Capacidad 2015	80,0%	NORM	77,0%	83,0%	0%
41 Capacidad 2016	85,0%	NORM	82,0%	88,0%	0%
42 Capacidad 2017	90,0%	NORM	87,0%	93,0%	0%

Fuente: elaboración propia

A continuación se presenta los resultados obtenidos para la simulación de escenarios múltiples de riesgo bajo la técnica de Monte Carlo.

Tabla 9. Resultados del análisis de riesgo bajo simulación Monte Carlo según la plataforma Risk Master

RISK ANALYSIS RESULTS Carnicoop (Risk Master)

	VAN básico	TIR
Expected value	1.941.869.891	35,74%
Standard deviation	478.239.033	3,23%
Minimum	690.907.021	26,94%
Maximum	3.226.853.421	44,39%
Coefficient of variation	24,63%	9,02%
Probability of negative outcome	0,0%	0,0%

Fuente: elaboración propia

Figura 4. Distribución de probabilidad del VAN bajo la plataforma Risk Master

Carnicoop (Risk Master) Frequency Distribution of VAN básico

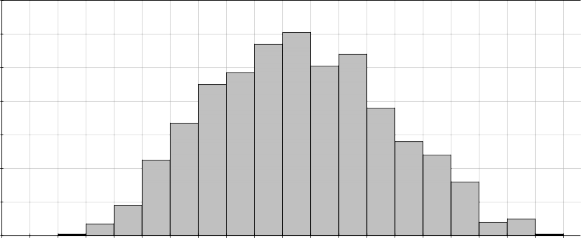
0,14

0,12

0,1

probability

0,08

0,06

0,04

0,02

500.000.000

650.000.000

800.000.000

950.000.000

1.100.000.000

1.250.000.000

1.400.000.000

1.550.000.000

1.700.000.000

1.850.000.000

2.000.000.000

2.150.000.000

2.300.000.000

2.450.000.000

2.600.000.000

2.750.000.000

2.900.000.000

3.050.000.000

3.200.000.000

3.350.000.000

3.500.000.000

Fuente: elaboración propia

Figura 5. Distribución de frecuencia acumulada del VAN bajo la plataforma Risk Master

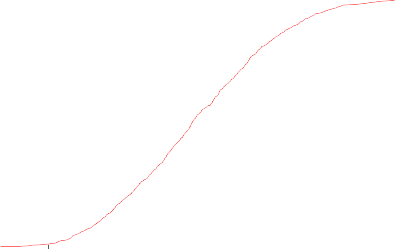
Carnicoop (Risk Master) Cumulative Distribution of VAN básico

100%

80%

probability

60%

40%

20%

0 500.000.000 1.000.000.000 1.500.000.000 2.000.000.000 2.500.000.000 3.000.000.000 3.500.000.

Fuente: elaboración propia

Figura 6. Distribución de probabilidad de la TIR bajo la plataforma Risk Master

Carnicoop (Risk Master) Frequency Distribution of TIR

0,14

0,12

0,1

probability

0,08

0,06

0,04

0,02

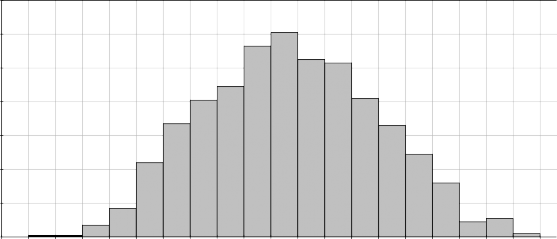
26,00% 27,00% 28,00% 29,00% 30,00% 31,00% 32,00% 33,00% 34,00% 35,00% 36,00% 37,00% 38,00% 39,00% 40,00% 41,00% 42,00% 43,00% 44,00% 45,00% 46,00

Fuente: elaboración propia

Figura 7. Distribución de probabilidad de la TIR bajo la plataforma Risk Master

Carnicoop (Risk Master) Cumulative Distribution of TIR

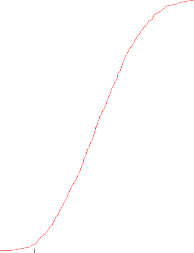
100%

80%

probability

60%

40%

20%

0,00% 5,00% 10,00% 15,00% 20,00% 25,00% 30,00% 35,00% 40,00% 45,00% 50,

Fuente: elaboración propia

Bajo la plataforma Risk Master, los resultados arrojan un riesgo medio-medio puesto que supera un coeficiente de variación del 20%, más no llega a presentar probabilidad de retorno negativo, lo cual es positivo para el proyecto.

CONCLUSIONES

El alcance de este trabajo se limita al análisis de riesgo con base en el uso de estadísticas de precios del mercado de matadores locales, entorno macroeconómico y datos de capacidad de planta, no se consideran riesgos asociados a robo y contrabando de ganado, riesgos microbiológicos, ni aquellos relacionados con el comercio internacional como el posible efecto de un Tratado de Libre Comercio con Colombia, dado que esta información no está contenida en el estudio de factibilidad.

Las variables de riesgo más sensibles o de mayor fueron efectivamente los precios de los boletos de res y cerdos derivados como función de los precios de mercado, y las capacidades de planta. Las variables macroeconómicas no tuvieron efectos fuertes en el análisis de sensibilidad.

Dentro del alcance del trabajo el análisis de riesgo arrojó resultados de riesgo medio con un coeficiente de variación menor al 30% y una probabilidad de retorno negativo de cero.

Para contar con un panorama más amplio de la medición del riesgo, se considera necesario incorporar los riesgos anotados en la conclusión 1 y ver su efecto en los flujos de efectivo tanto en escenario estático como dinámico.
REFERENCIAS BIBLIOGRAFICAS

Chavas, J. P. (2004). Risk Analysis in Theory and Practice. London: Elsevier Academic Press.

Hang, N., & Ying, H. (2006). Simulation Techniques in Financial Risk Management. New Jersey: John Wiley & Sons.

Jackel, P. (2002). Monte Carlo Methods in Finance. West Sussex: John Wiley & Sons. Sapag , N., & Sapag, C. (2008). Preparación y Evaluación de Proyectos. Bogotá: McGraw-

Hill Interamericana.

Savvides, C. S. (1994). Risk Analysis in Investment Appraisal. Project Appraisal, 3-18. Wayne, W. (2001). Simulation Modeling using @Risk. Palisade Inc: Duxbury.

Volumen 3, número 1, articulo 1

Enero-junio 2017

Publicado 1 de enero, 2017

Análisis de riesgo bajo simulación Monte Carlo para un proyecto de industrialización de carne de bovino

RESUMEN

Palabras clave: Análisis de riesgo, simulación Monte Carlo, industria de carne

ABSTRACT

Key words: Risk analysis, Monte Carlo simulation, meat industry

INTRODUCCION

REFERENTE TEORICO

METODOLOGIA

Datos

2.3 Modelado

RESULTADOS Y DISCUSION

Modelación

Tabla 1. Tabla de parámetros del modelo

Tabla 2. Plan de producción y ventas

Tabla 3. Flujo de efectivo del proyecto

Análisis de sensibilidad y riesgo

Figura 1. Análisis de sensibilidad para las variables del proyecto

Tabla 4. ARIMA, usando las observaciones 1982-2011 (T = 30)

Tabla 5. ARIMA, usando las observaciones 1981-2011 (T = 31) Variable dependiente: (1-L) l_Tasa_de_interés (TBP)

Tabla 6. Pronóstico del Indice de Precios al Consumidor como predictor de la tasa de inflación local. Intervalos de confianza al 95%

Tabla 7. Pronóstico de la tasa de interés (Tasa Básica Pasiva). Intervalos de confianza al 95%

Figura 2. Distribución de probabilidad para el precio local de la carne de res

Figura 3. Distribución de probabilidad el precio local de la carne de cerdo

Tabla 8. Tabla de variables de riesgo

Carnicoop (Risk Master)

Tabla 9. Resultados del análisis de riesgo bajo simulación Monte Carlo según la plataforma Risk Master

Figura 4. Distribución de probabilidad del VAN bajo la plataforma Risk Master

Figura 5. Distribución de frecuencia acumulada del VAN bajo la plataforma Risk Master

Figura 6. Distribución de probabilidad de la TIR bajo la plataforma Risk Master

Figura 7. Distribución de probabilidad de la TIR bajo la plataforma Risk Master

CONCLUSIONES

REFERENCIAS BIBLIOGRAFICAS